Kinematic Equations and Their Applications

The video tutorial explains a kinetic equation that does not involve time, useful for solving problems with given velocities, accelerations, and displacements. It covers rearranging kinematic equations to solve for time, understanding average velocity and displacement, and algebraic manipulation. The tutorial also demonstrates multiplying binomials using the FOIL method, leading to the derivation of a final equation. The instructor emphasizes the algebraic complexity and the elusive understanding of the equation's meaning.

What is a key characteristic of the kinematic equation introduced in the video?

• It is primarily used for energy calculations.

• It involves time as a variable.

• It is only applicable to constant velocity scenarios.

• It does not involve time as a variable.

What is the first step in rearranging the kinematic equation for velocity to solve for time?

• Subtract initial velocity from both sides.

• Divide both sides by time.

• Add initial velocity to both sides.

• Multiply both sides by acceleration.

How is average velocity defined in the context of the video?

• The difference between final and initial velocities.

• The product of initial and final velocities.

• The sum of initial and final velocities divided by two.

• The initial velocity divided by the final velocity.

What is the purpose of substituting expressions into the displacement equation?

• To eliminate the need for acceleration.

• To simplify the equation for easier understanding.

• To solve for initial velocity.

• To introduce a new variable.

What algebraic method is used to simplify the multiplication of two binomials in the video?

• Quadratic formula

• Completing the square

• Substitution method

• FOIL method

What happens to the v terms when multiplying the binomials?

• They form a quadratic equation.

• They cancel each other out.

• They remain unchanged.

• They add up to a larger term.

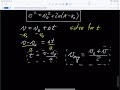
What is the final form of the kinematic equation derived in the video?

• v = v_0 + at

• v^2 = v_0^2 + 2a(x - x_0)

• x = x_0 + vt

• a = (v - v_0)/t

Why is the derived kinematic equation considered elusive in terms of understanding?

• Its meaning is not immediately clear.

• It lacks practical applications.

• It involves too many variables.

• It requires complex calculus.

What is the significance of the term 2a(x - x_0) in the final equation?

• It is a constant factor.

• It accounts for the initial velocity.

• It is related to the displacement and acceleration.

• It represents the change in velocity.

What is the main challenge in using the derived kinematic equation?

• Understanding its algebraic manipulation.

• Finding the correct values for variables.

• Memorizing the equation.

• Applying it to real-world scenarios.