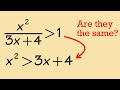
Understanding Rational Inequalities and Their Solutions

The video tutorial covers solving inequalities, focusing on quadratic and rational inequalities. It explains the differences between equations and inequalities, emphasizing the importance of sign changes when multiplying or dividing across inequalities. The tutorial demonstrates solving quadratic inequalities using factorization and interval notation. It also addresses rational inequalities, highlighting the need to consider points where the denominator is zero. The use of number lines to determine solution intervals is explained, and the video concludes with practice recommendations.

What is the main difference between the two inequalities discussed in the video?

• The first inequality involves a rational expression.

• The second inequality involves a rational expression.

• The first inequality has no solution.

• Both inequalities are identical.

Why is it important to be cautious when multiplying or dividing across inequalities?

• It can make the inequality unsolvable.

• It may require switching the inequality sign.

• It can introduce complex numbers.

• It can change the inequality to an equation.

What happens to the inequality sign when multiplying or dividing by a negative number?

• It becomes undefined.

• It becomes an equation.

• It switches direction.

• It remains the same.

What is the result of multiplying both sides of an inequality by a positive number?

• The inequality sign switches.

• The inequality becomes an equation.

• The inequality becomes undefined.

• The inequality sign remains the same.

What is the first step in solving the inequality x^2 - 3x - 4 > 0?

• Divide both sides by x.

• Multiply both sides by 3.

• Add 4 to both sides.

• Factor the quadratic expression.

What is the result of factoring x^2 - 3x - 4?

• (x - 3)(x + 1)

• (x + 4)(x - 1)

• (x - 4)(x + 1)

• (x - 2)(x + 2)

Which numbers are critical when solving x^2 - 3x - 4 > 0?

• -1 and 4

• 3 and 4

• -2 and 3

• 0 and 1

What is the significance of open circles on the number line?

• They indicate included points.

• They indicate excluded points.

• They indicate zero points.

• They indicate positive points.

What is the significance of the number 4 in the first inequality?

• It is a solution.

• It is a critical point.

• It is a boundary.

• It is a midpoint.

How is the solution to x^2 - 3x - 4 > 0 represented in interval notation?

• (-∞, -1) ∪ (4, ∞)

• (-∞, 4) ∪ (1, ∞)

• (-1, 4)

• (0, ∞)