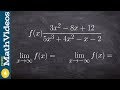
Understanding Asymptotes in Rational Functions

The video tutorial covers the identification of asymptotes in rational functions. It begins with an introduction to polynomial and rational functions, followed by a detailed explanation of how to identify horizontal asymptotes when the degree of the numerator is less than, equal to, or greater than the degree of the denominator. The tutorial also discusses slant or oblique asymptotes and provides methods for simplifying the process, including the use of long division and leading coefficients.

Why is it important to think critically about polynomial and trigonometric functions?

• To understand their behavior and properties

• To avoid using calculators

• To memorize their graphs

• To solve them quickly

What is the first step in identifying asymptotes in rational functions?

• Graphing the function

• Calculating the derivative

• Comparing the degrees of the numerator and denominator

• Finding the roots

In the context of rational functions, what is an asymptote?

• A point where the graph intersects the axis

• A line that the graph approaches but never touches

• A point of discontinuity

• A curve that the graph follows

What is the role of the degree of the numerator in determining the type of asymptote?

• It has no role

• It determines the vertical asymptote

• It determines the horizontal asymptote

• It determines the slant asymptote

What is the significance of the degree of the denominator in determining the horizontal asymptote?

• It determines the slope of the asymptote

• It determines the y-intercept of the asymptote

• It determines the x-intercept of the asymptote

• It helps compare with the numerator to find the asymptote

When the degree of the numerator is less than the degree of the denominator, what is the horizontal asymptote?

• y = 1

• y = 0

• y = infinity

• y = -1

What happens to the graph of a function as it approaches its horizontal asymptote?

• It diverges away from the asymptote

• It oscillates around the asymptote

• It approaches but never touches the asymptote

• It crosses the asymptote

What is the behavior of a graph with a horizontal asymptote as it goes to infinity?

• It rises indefinitely

• It oscillates

• It falls indefinitely

• It approaches the horizontal asymptote

What is the end behavior of a function with a horizontal asymptote of y = 0?

• It approaches y = -1 as x goes to infinity

• It approaches y = 0 as x goes to infinity

• It approaches y = 1 as x goes to infinity

• It approaches y = infinity as x goes to infinity

What is the behavior of a graph with a horizontal asymptote as it goes to negative infinity?

• It oscillates around the horizontal asymptote

• It becomes vertical

• It diverges from the horizontal asymptote

• It approaches the horizontal asymptote