What is the Student t distribution often used for?
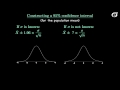
Understanding the t Distribution
Interactive Video
•
Mathematics
•
11th - 12th Grade
•
Hard
Thomas White
FREE Resource
Read more
33 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Estimating the median of a population
Estimating the mean of a population when the standard deviation is known
Estimating the mean of a population when the standard deviation is unknown
Estimating the variance of a population
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Why can't we use the population standard deviation in practice?
It is always one
It is often unknown
It is always zero
It is a constant
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What replaces the population standard deviation in the t distribution?
Sample median
Sample variance
Sample standard deviation
Sample mean
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is a key characteristic of the t distribution?
It has a higher peak than the normal distribution
It is always symmetric
It has heavier tails than the normal distribution
It is always skewed
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the degrees of freedom for a sample of size n?
n/2
n
n+1
n-1
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What happens to the t distribution as the degrees of freedom increase?
It becomes identical to the standard normal distribution
It becomes more skewed
It becomes more variable
It becomes less symmetric
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the shape of the t distribution compared to the standard normal distribution?
It is identical
It is flatter with heavier tails
It is more peaked
It is skewed
Create a free account and access millions of resources
Similar Resources on Wayground

24 questions
Standard Normal Distribution Concepts
Interactive video
•
9th - 10th Grade

33 questions
Statistical Measures and Sampling Methods
Interactive video
•
9th - 10th Grade

22 questions
Confidence Intervals and Sample Proportions
Interactive video
•
9th - 10th Grade

23 questions
Probability and Distributions Concepts
Interactive video
•
9th - 10th Grade

36 questions
Sampling Distribution and Central Limit Theorem
Interactive video
•
9th - 10th Grade

26 questions
Normal Distribution Concepts and Z-scores
Interactive video
•
9th - 10th Grade

26 questions
Understanding Normal Curves and Sigma
Interactive video
•
9th - 10th Grade

29 questions
Understanding Standard Deviation and Variance
Interactive video
•
9th - 10th Grade
Popular Resources on Wayground

25 questions
Equations of Circles
Quiz
•
10th - 11th Grade

30 questions
Week 5 Memory Builder 1 (Multiplication and Division Facts)
Quiz
•
9th Grade

33 questions
Unit 3 Summative - Summer School: Immune System
Quiz
•
10th Grade

10 questions
Writing and Identifying Ratios Practice
Quiz
•
5th - 6th Grade

36 questions
Prime and Composite Numbers
Quiz
•
5th Grade

14 questions
Exterior and Interior angles of Polygons
Quiz
•
8th Grade

37 questions
Camp Re-cap Week 1 (no regression)
Quiz
•
9th - 12th Grade

46 questions
Biology Semester 1 Review
Quiz
•
10th Grade