15 Q
9th - 12th

20 Q
9th - Uni
55 Q
9th - 12th
17 Q
9th - Uni

20 Q
11th - Uni

50 Q
12th

10 Q
9th - 12th

59 Q
9th - 12th

32 Q
12th

89 Q
9th - 12th
70 Q
9th - 12th
30 Q
9th - 12th

10 Q
9th - 12th
16 Q
9th - 12th
20 Q
9th - 12th

150 Q
12th
15 Q
8th - Uni

20 Q
9th - Uni
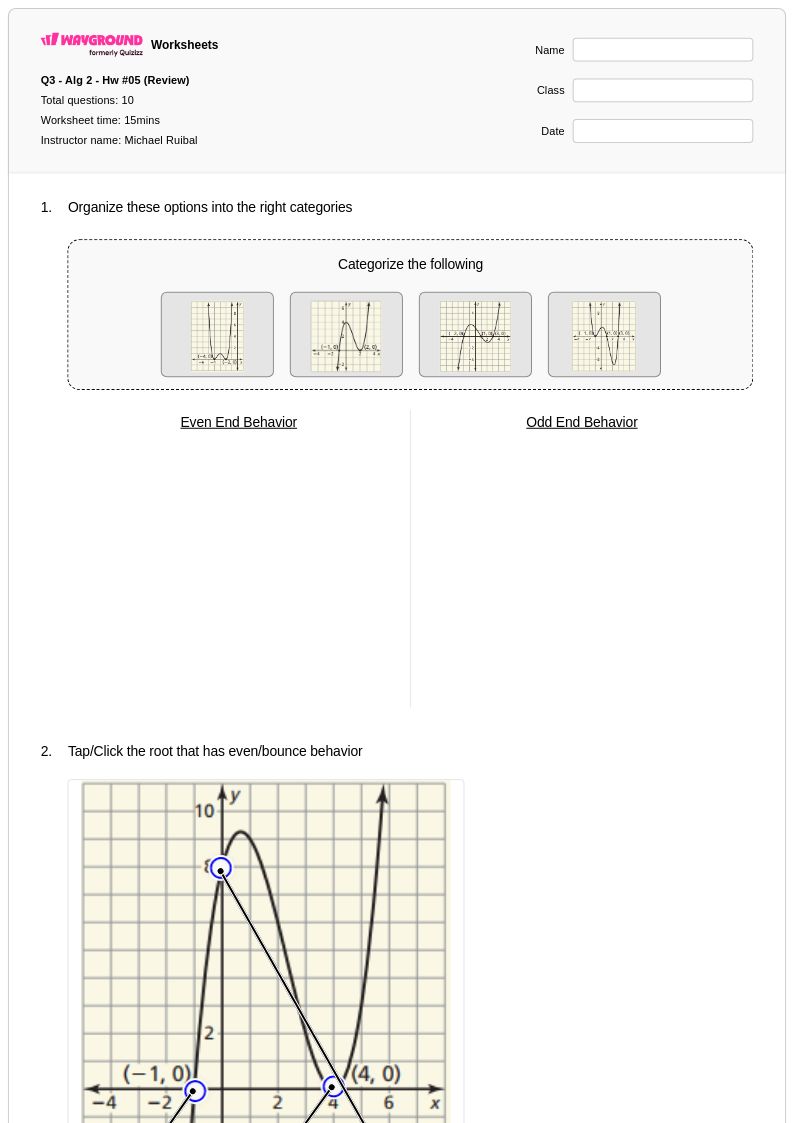
10 Q
12th
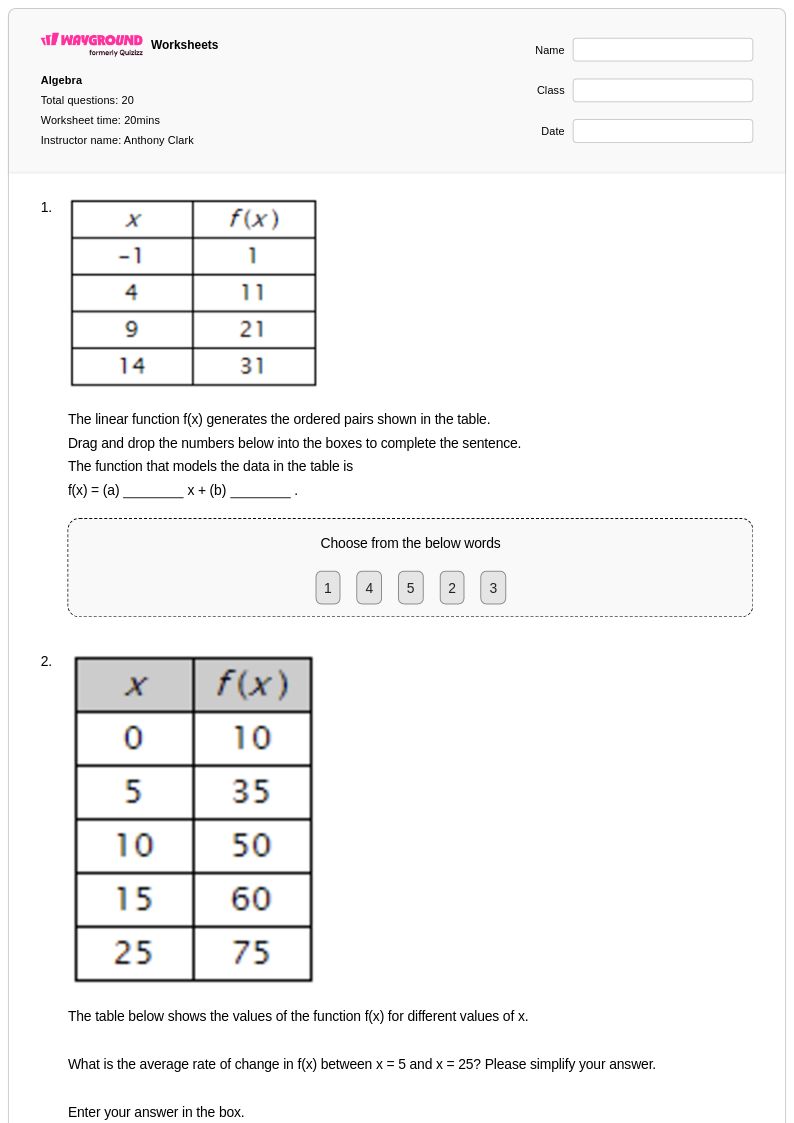
20 Q
9th - Uni

51 Q
9th - 12th

10 Q
12th
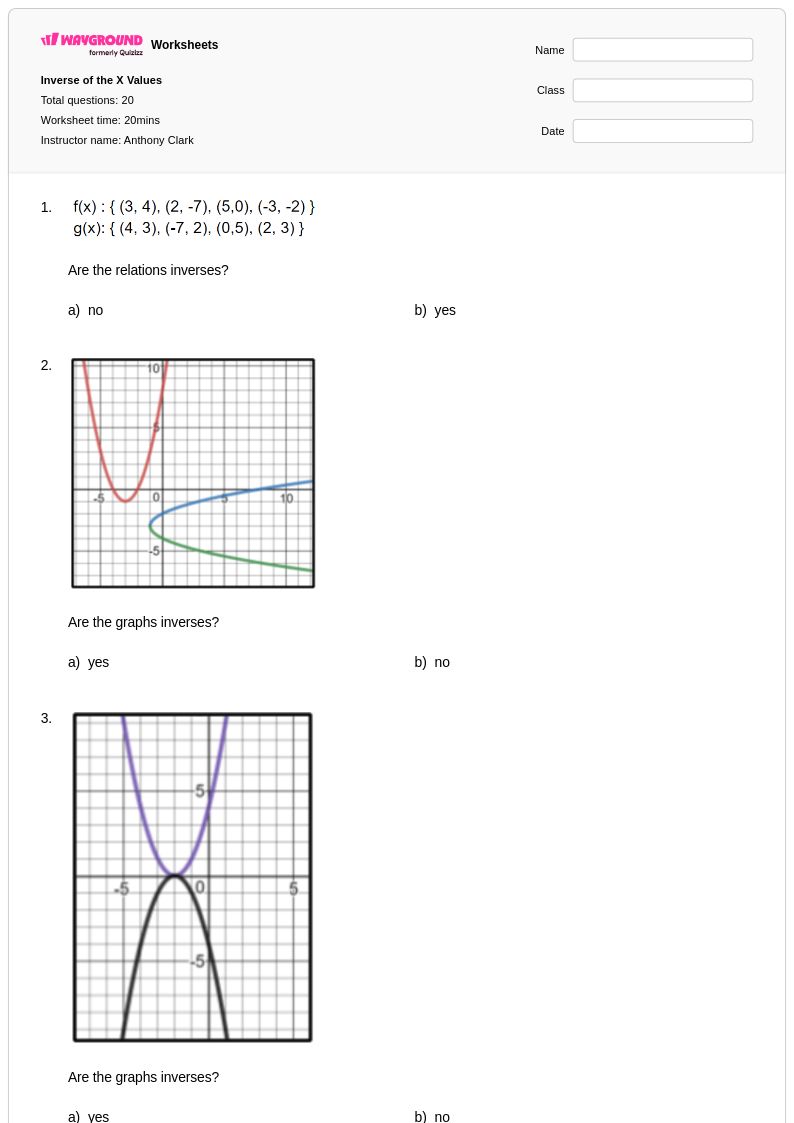
20 Q
12th - Uni
Explore Other Subject Worksheets for ระดับ 12
สำรวจแผ่นงาน กราฟขั้นบันได ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 12
แบบฝึกหัดกราฟขั้นบันไดสำหรับนักเรียนชั้นมัธยมศึกษาปีที่ 6 (เกรด 12) จาก Wayground (เดิมคือ Quizizz) ให้แบบฝึกหัดที่ครอบคลุมเกี่ยวกับฟังก์ชันคงที่แบบแบ่งช่วงและการประยุกต์ใช้ในชีวิตจริง แบบฝึกหัดเฉพาะทางเหล่านี้ช่วยเสริมสร้างความสามารถของนักเรียนในการตีความ สร้าง และวิเคราะห์ฟังก์ชันขั้นบันไดในบริบททางคณิตศาสตร์ต่างๆ รวมถึงอัตราค่าไปรษณีย์ ค่าโดยสารแท็กซี่ อัตราภาษีเงินได้ และระบบการเรียกเก็บค่าสาธารณูปโภค นักเรียนจะได้พัฒนาทักษะที่สำคัญในการอ่านกราฟที่ไม่ต่อเนื่อง การระบุข้อจำกัดของโดเมนและเรนจ์ และความเข้าใจพฤติกรรมของฟังก์ชันที่มีการกระโดดแบบไม่ต่อเนื่อง แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียดและมีให้ดาวน์โหลดเป็นไฟล์ PDF ที่สะดวกต่อการพิมพ์ฟรี ช่วยให้นักเรียนสามารถฝึกฝนโจทย์ปัญหาต่างๆ ที่ค่อยๆ เสริมสร้างความเข้าใจในแนวคิดการสร้างกราฟขั้นสูงนี้ ซึ่งจำเป็นสำหรับคณิตศาสตร์ระดับมหาวิทยาลัย
Wayground (เดิมคือ Quizizz) สนับสนุนครูผู้สอนคณิตศาสตร์ด้วยชุดทรัพยากรเกี่ยวกับกราฟขั้นบันไดที่สร้างโดยครูผู้สอนจำนวนมาก โดยดึงข้อมูลจากแบบฝึกหัดคุณภาพสูงนับล้านรายการ ซึ่งสามารถค้นหาและกรองได้อย่างง่ายดายตามวัตถุประสงค์การเรียนรู้และระดับทักษะที่เฉพาะเจาะจง การจัดเรียงมาตรฐานที่แข็งแกร่งของแพลตฟอร์มนี้ทำให้มั่นใจได้ว่าสื่อการเรียนรู้เกี่ยวกับกราฟขั้นบันไดสำหรับชั้นมัธยมศึกษาปีที่ 6 ตรงตามข้อกำหนดทางวิชาการที่เข้มงวด ในขณะที่เครื่องมือการปรับระดับความยากง่ายในตัวช่วยให้ครูสามารถปรับแต่งแบบฝึกหัดให้เหมาะกับความสามารถของนักเรียนที่แตกต่างกันภายในห้องเรียนเดียวกันได้ แหล่งข้อมูลเหล่านี้มีให้เลือกทั้งในรูปแบบ PDF ที่สามารถพิมพ์ได้สำหรับงานแบบดั้งเดิมที่ใช้กระดาษและดินสอ และรูปแบบดิจิทัลสำหรับประสบการณ์การเรียนรู้แบบโต้ตอบ ครูสามารถวางแผนบทเรียนได้อย่างมีประสิทธิภาพ ให้การแก้ไขปัญหาที่ตรงเป้าหมายสำหรับนักเรียนที่ประสบปัญหา ให้โอกาสในการเสริมสร้างความรู้สำหรับผู้เรียนที่มีความสามารถสูง และให้การฝึกฝนทักษะอย่างสม่ำเสมอซึ่งเสริมสร้างเหตุผลทางคณิตศาสตร์ที่ซับซ้อนซึ่งจำเป็นต่อการเรียนรู้ฟังก์ชันขั้นบันไดและการแสดงกราฟของฟังก์ชันเหล่านั้น
