
8 คิว
5th
15 คิว
5th

15 คิว
5th
15 คิว
4th - 7th
34 คิว
5th
20 คิว
4th - 6th

8 คิว
5th - 7th

6 คิว
5th - 7th
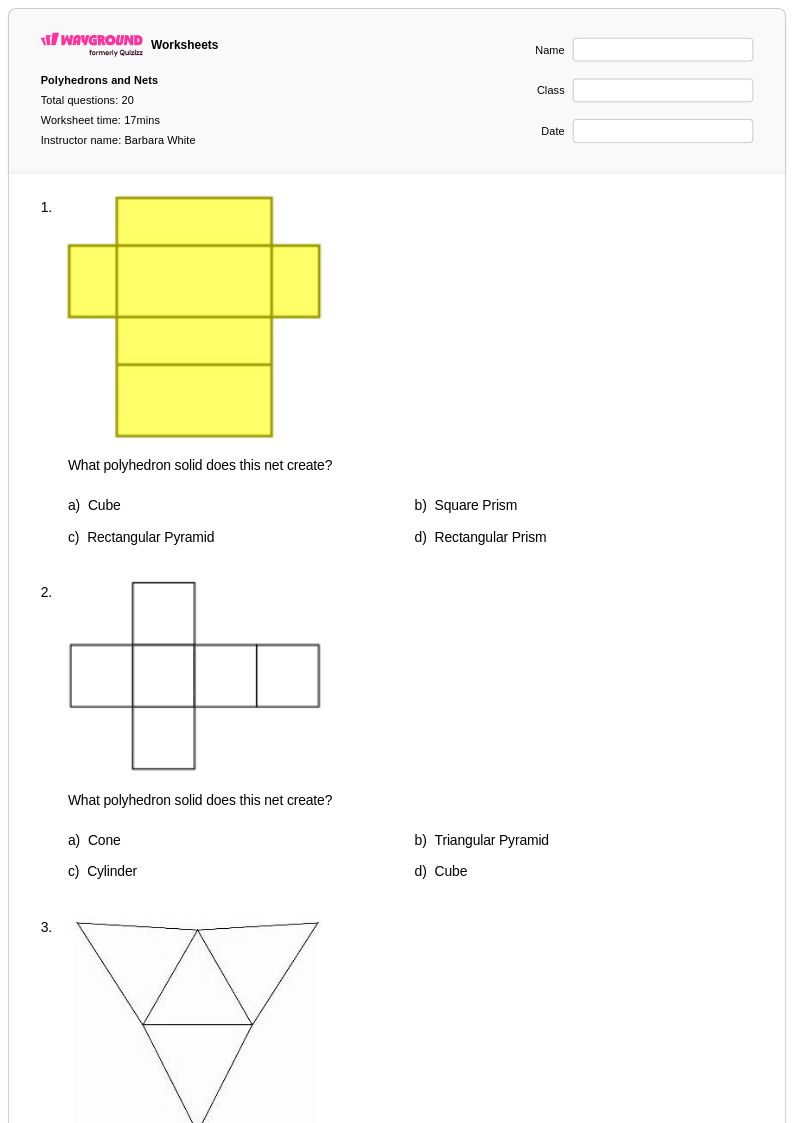
20 คิว
4th - 6th

14 คิว
5th - 6th

15 คิว
3rd - 5th

14 คิว
5th - 6th
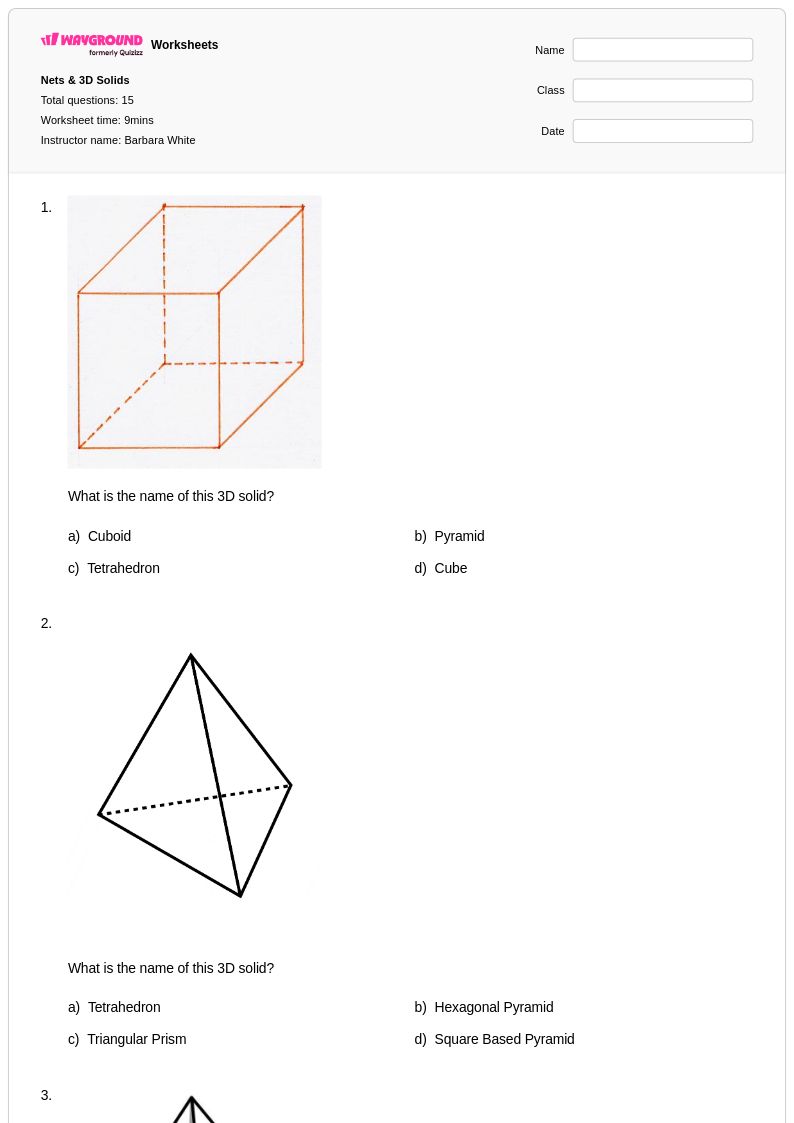
15 คิว
5th - 8th
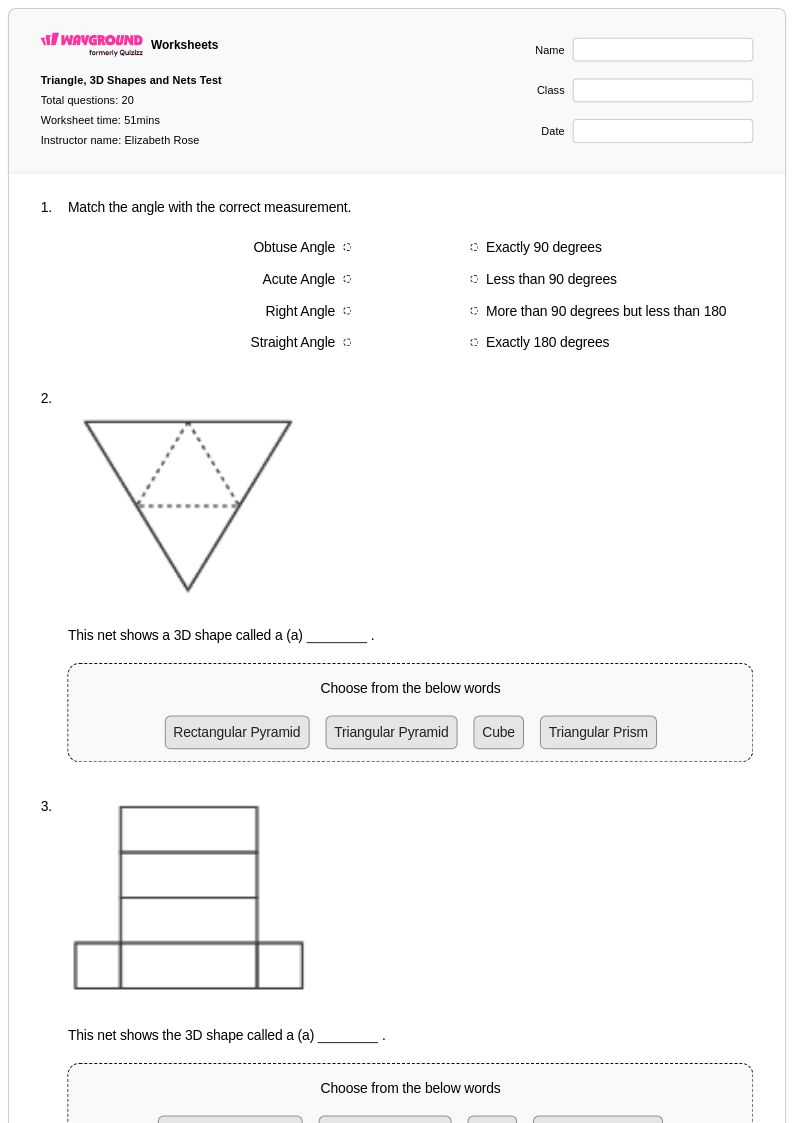
20 คิว
5th
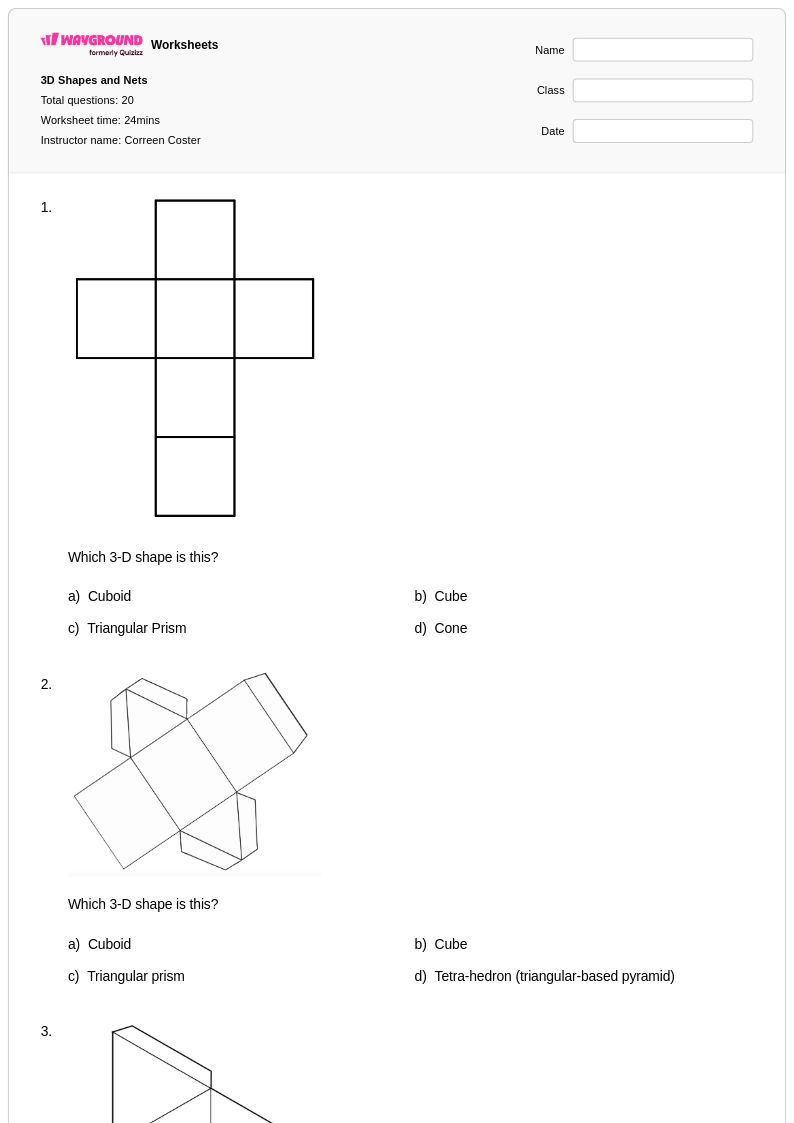
20 คิว
5th
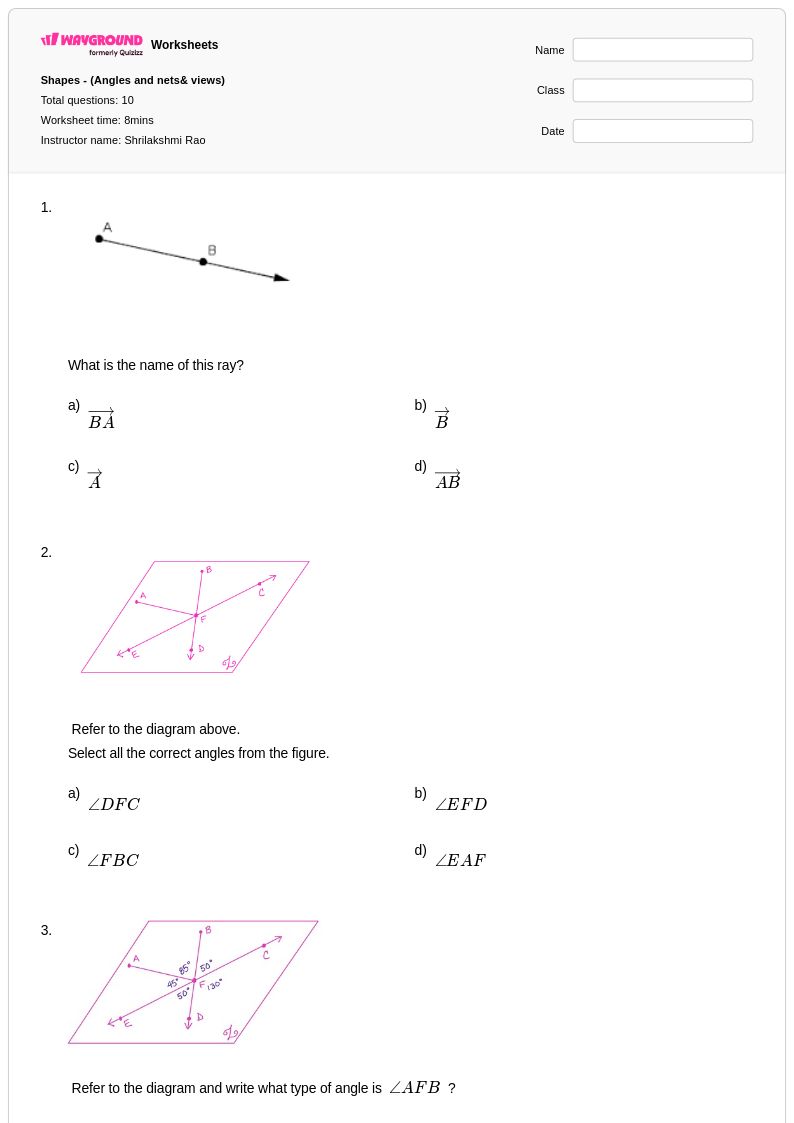
10 คิว
5th - 6th
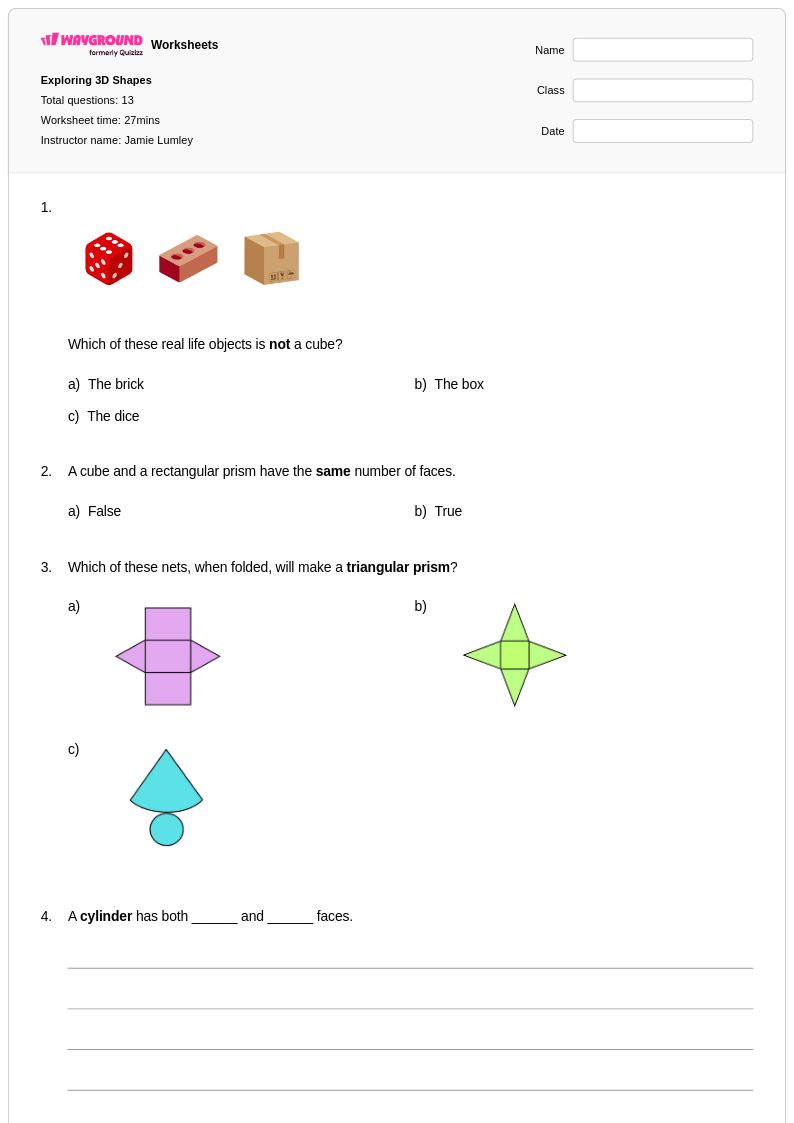
13 คิว
5th - Uni

14 คิว
5th - Uni

11 คิว
5th

12 คิว
5th

15 คิว
5th - Uni

9 คิว
2nd - Uni
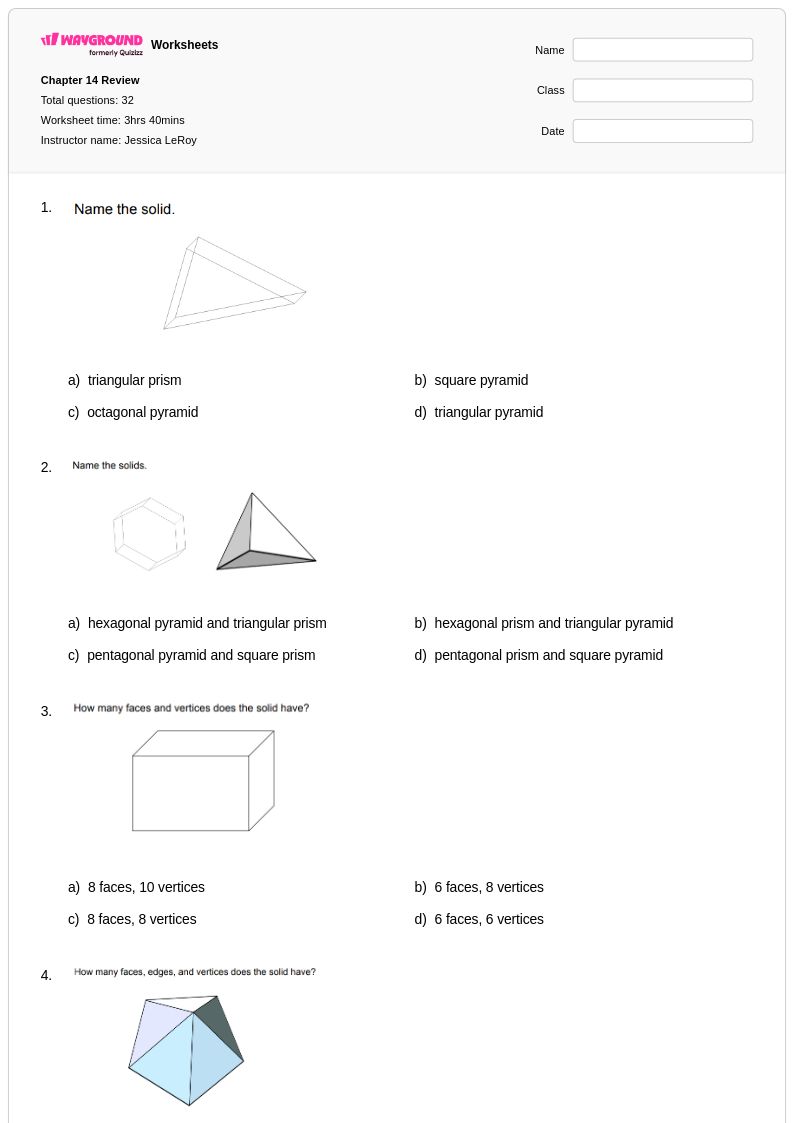
32 คิว
5th

11 คิว
5th - 8th
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 5
สำรวจแผ่นงาน ตาข่าย ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 5
แบบฝึกหัดเรื่องรูปทรงคลี่ (Nets) สำหรับนักเรียนชั้นประถมศึกษาปีที่ 5 จาก Wayground (เดิมชื่อ Quizizz) เป็นแบบฝึกหัดที่ครอบคลุมในการมองเห็นและเข้าใจวิธีการคลี่รูปทรงสามมิติไปเป็นรูปทรงสองมิติ แบบฝึกหัดที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยให้นักเรียนพัฒนาทักษะการคิดเชิงพื้นที่ ขณะที่พวกเขาเรียนรู้ที่จะระบุว่ารูปทรงคลี่ใดสามารถพับเป็นรูปทรงเรขาคณิตเฉพาะ เช่น ลูกบาศก์ ปริซึมสี่เหลี่ยม พีระมิด และทรงกระบอก แบบฝึกหัดเหล่านี้เสริมสร้างความสามารถในการคิดเชิงวิเคราะห์โดยท้าทายให้นักเรียนจัดการกับรูปทรงในใจและคาดการณ์ผลลัพธ์ ในขณะเดียวกันก็สร้างแนวคิดพื้นฐานทางเรขาคณิตที่จำเป็นสำหรับการเรียนรู้คณิตศาสตร์ขั้นสูง ครูสามารถเข้าถึงเฉลยคำตอบทั้งหมดควบคู่ไปกับแหล่งข้อมูลที่พิมพ์ได้ฟรีเหล่านี้ ทำให้การประเมินและการสอนแบบมีแนวทางมีประสิทธิภาพและประสิทธิผลมากขึ้น
Wayground มีแหล่งข้อมูลเรขาคณิตที่สร้างโดยครูจำนวนมาก ซึ่งสนับสนุนนักการศึกษาด้วยแบบฝึกหัดคุณภาพสูงนับล้านรายการที่สามารถค้นหาและกรองได้อย่างง่ายดายเพื่อให้ตรงกับวัตถุประสงค์การเรียนรู้และข้อกำหนดมาตรฐานเฉพาะของชั้นประถมศึกษาปีที่ 5 เครื่องมือปรับระดับความยากง่ายของแพลตฟอร์มนี้ช่วยให้ครูสามารถปรับแต่งกิจกรรมการคลี่รูปทรงเรขาคณิตให้เหมาะสมกับระดับทักษะที่แตกต่างกันในห้องเรียน เพื่อให้แน่ใจว่านักเรียนที่อ่อนล้าจะได้รับการสนับสนุนที่เหมาะสม ในขณะที่นักเรียนที่มีความสามารถสูงจะได้รับโจทย์เรขาคณิตที่ซับซ้อนมากขึ้น สื่อการเรียนรู้ที่หลากหลายเหล่านี้มีให้เลือกทั้งในรูปแบบไฟล์ PDF ที่สามารถพิมพ์ได้สำหรับการใช้งานในห้องเรียนแบบดั้งเดิม และรูปแบบดิจิทัลสำหรับสภาพแวดล้อมการเรียนรู้แบบโต้ตอบ ทำให้ครูผู้สอนมีความยืดหยุ่นในการบูรณาการการฝึกฝนการคลี่รูปทรงเรขาคณิตเข้ากับการวางแผนบทเรียน การแก้ไขปัญหาเฉพาะด้าน กิจกรรมเสริม และแบบฝึกหัดพัฒนาทักษะอย่างสม่ำเสมอในหลักสูตรเรขาคณิต
