
20 Hỏi
5th - Uni
20 Hỏi
5th - Uni
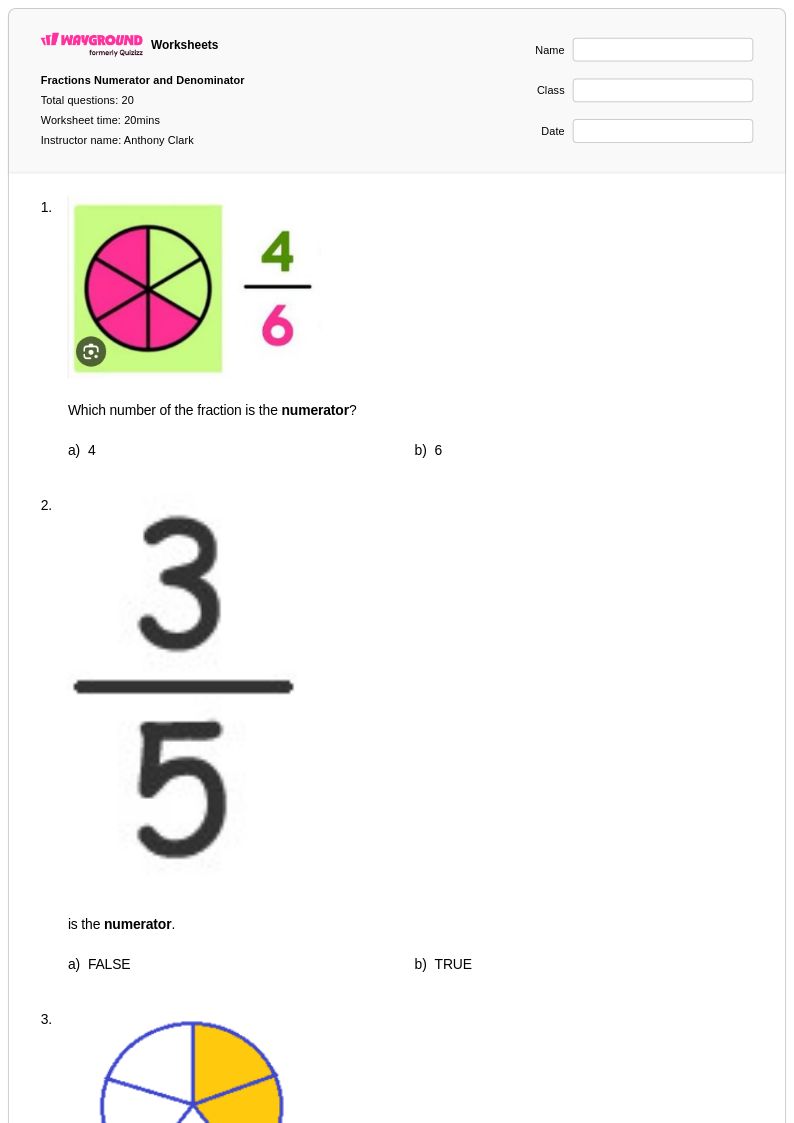
20 Hỏi
5th - Uni
10 Hỏi
5th
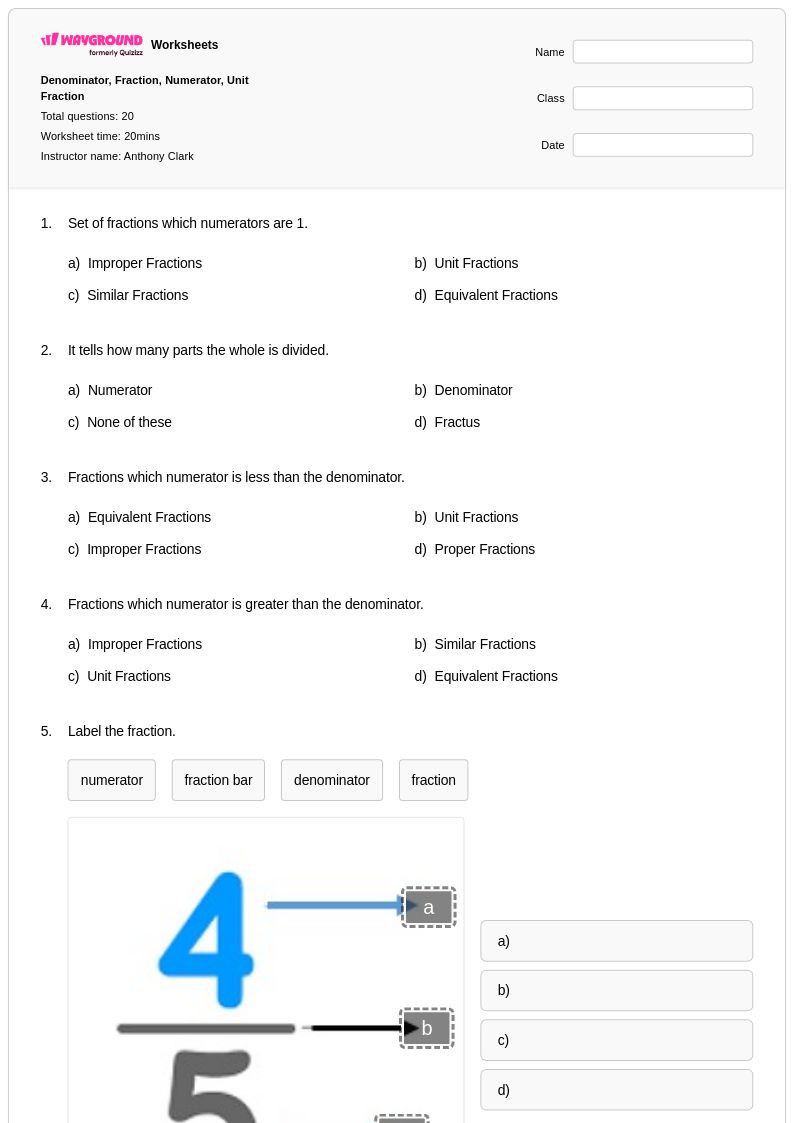
20 Hỏi
5th - Uni

20 Hỏi
4th - Uni
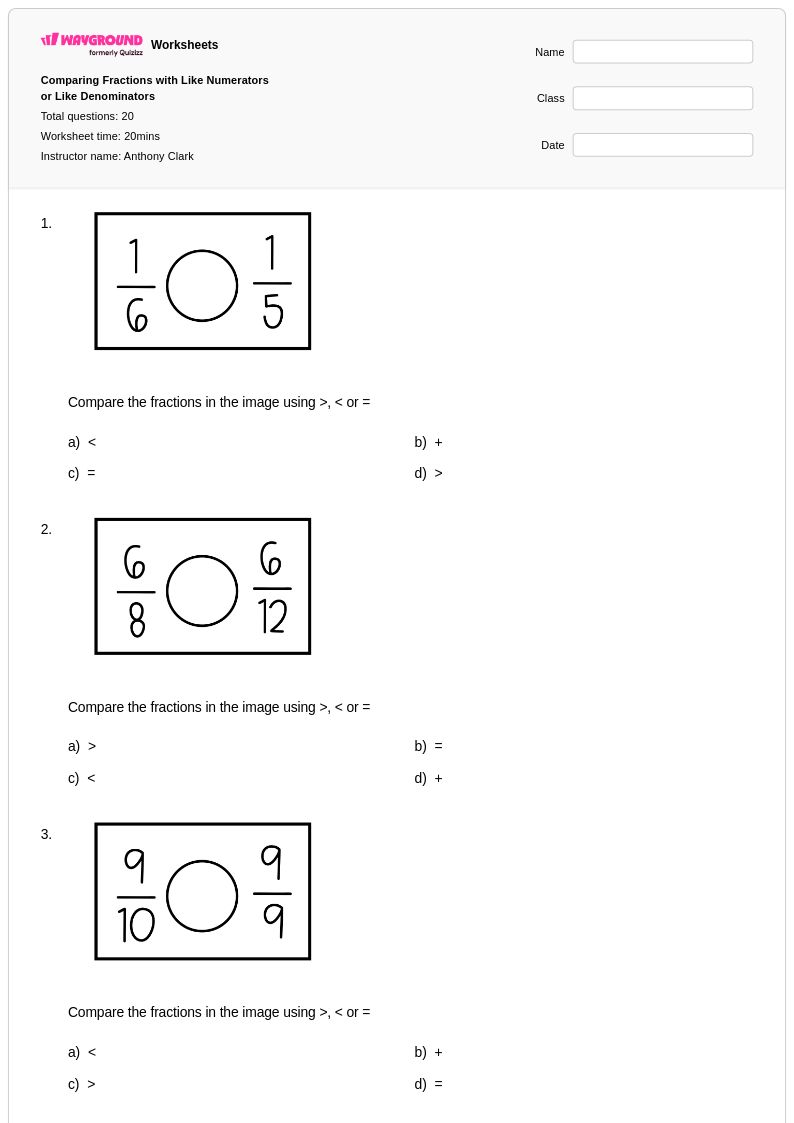
20 Hỏi
4th - Uni
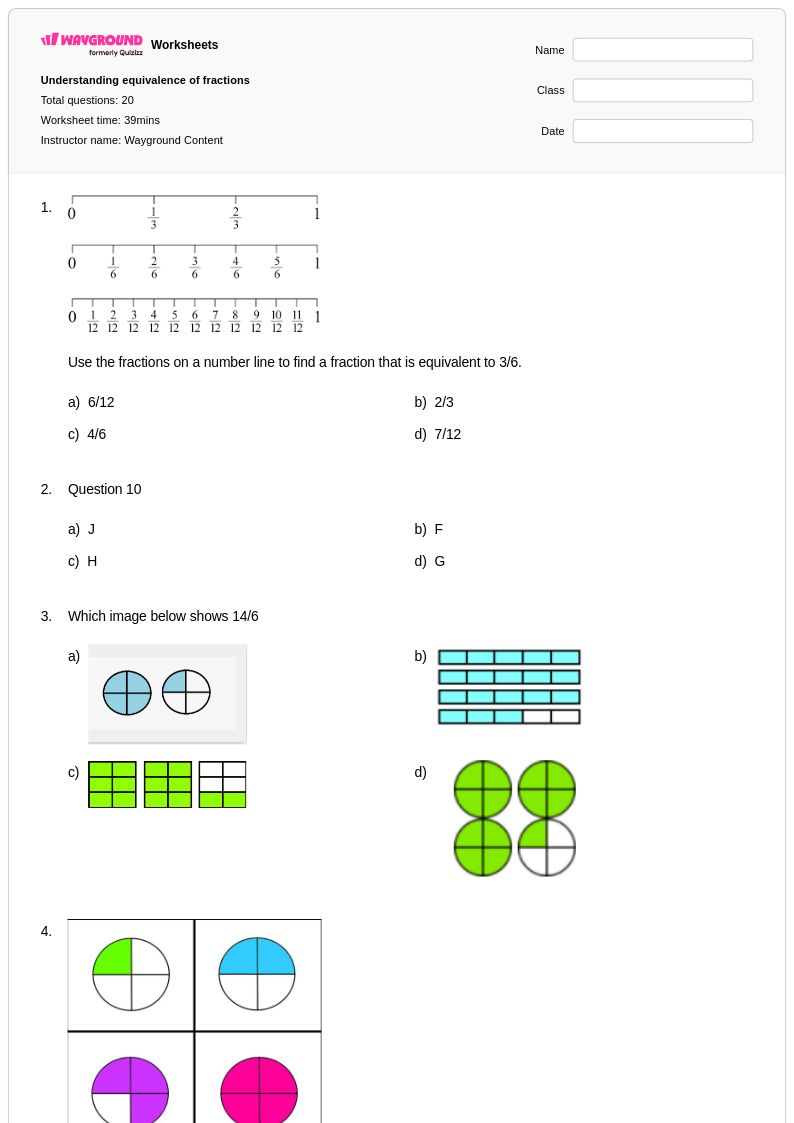
20 Hỏi
4th - 5th
30 Hỏi
5th

18 Hỏi
5th

10 Hỏi
5th

18 Hỏi
5th

20 Hỏi
5th - Uni

20 Hỏi
4th - Uni
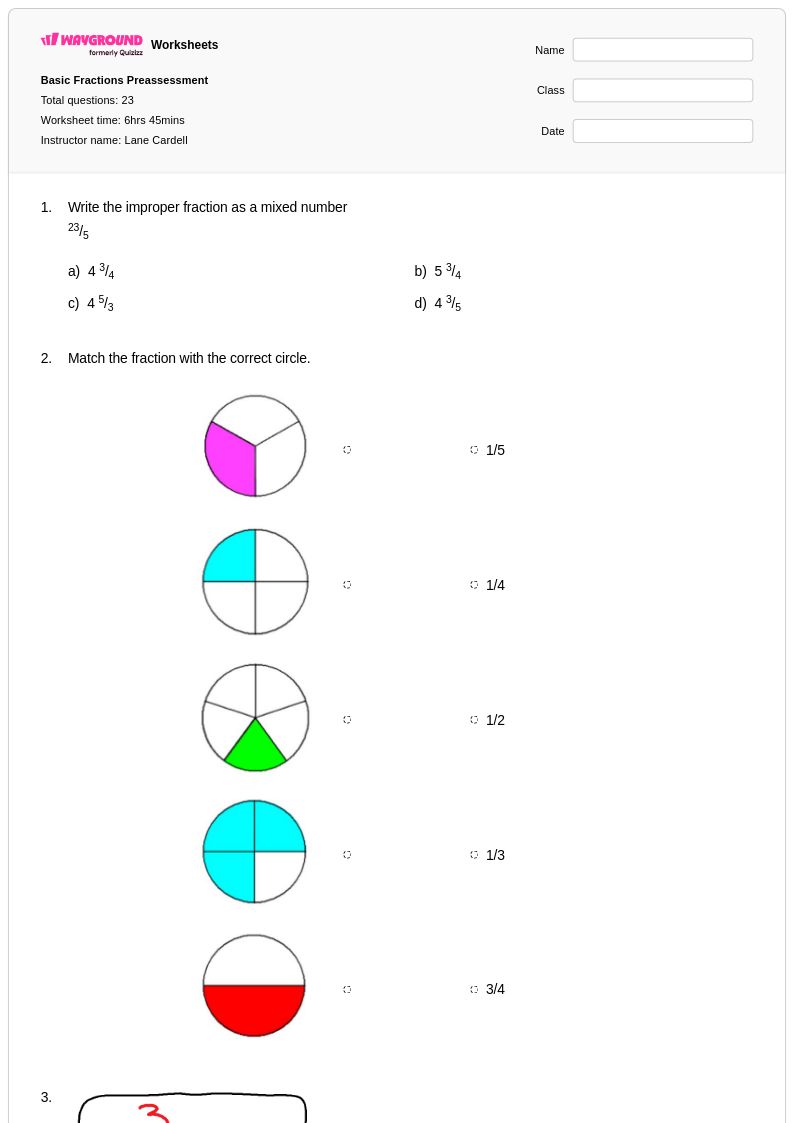
23 Hỏi
5th

20 Hỏi
5th - Uni

15 Hỏi
5th - 7th
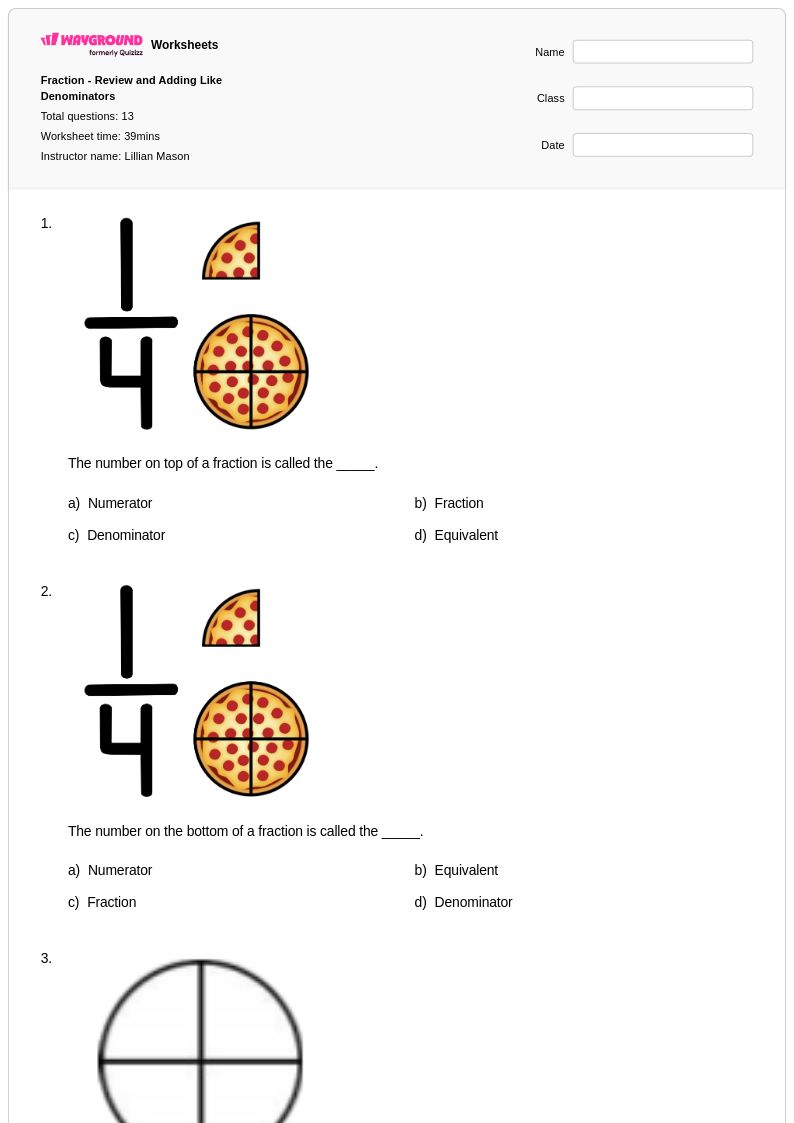
13 Hỏi
3rd - 5th

10 Hỏi
3rd - 5th

17 Hỏi
3rd - 5th

15 Hỏi
5th
20 Hỏi
5th - Uni

20 Hỏi
5th - Uni

14 Hỏi
4th - Uni
Khám phá ทำความเข้าใจเกี่ยวกับตัวเศษ Bảng tính theo cấp độ
Khám phá các bảng tính chủ đề khác cho ระดับ 5
สำรวจแผ่นงาน ทำความเข้าใจเกี่ยวกับตัวเศษ ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 5
การเข้าใจตัวเศษเป็นพื้นฐานสำคัญในวิชาคณิตศาสตร์ระดับชั้นประถมศึกษาปีที่ 5 และชุดแบบฝึกหัดที่ครอบคลุมของ Wayground มอบแหล่งข้อมูลที่ออกแบบมาอย่างเชี่ยวชาญเพื่อเสริมสร้างความเข้าใจในแนวคิดเรื่องเศษส่วนที่สำคัญนี้ แบบฝึกหัดเหล่านี้จะแนะนำนักเรียนอย่างเป็นระบบในการระบุ วิเคราะห์ และทำงานกับตัวเศษ ขณะที่พวกเขาพัฒนาความเข้าใจที่ลึกซึ้งยิ่งขึ้นว่าตัวเลขด้านบนในเศษส่วนแสดงถึงส่วนที่นับหรือพิจารณาอย่างไร แบบฝึกหัดจะค่อยๆ พัฒนาไปตามลำดับ ตั้งแต่แบบฝึกหัดการระบุตัวเศษขั้นพื้นฐานไปจนถึงการประยุกต์ใช้ที่ซับซ้อนมากขึ้น ซึ่งนักเรียนต้องเปรียบเทียบ เรียงลำดับ และจัดการเศษส่วนตามตัวเศษ แบบฝึกหัดที่พิมพ์ได้แต่ละแผ่นมีเฉลยโดยละเอียด ช่วยให้ครูสามารถให้ข้อเสนอแนะได้ทันทีและสนับสนุนการฝึกฝนของนักเรียนอย่างอิสระ ในขณะที่รูปแบบ PDF ฟรีช่วยให้แจกจ่ายในห้องเรียนและมอบหมายการบ้านได้ง่าย
คลังข้อมูลขนาดใหญ่ของ Wayground ซึ่งมีแหล่งข้อมูลที่สร้างโดยครูหลายล้านรายการ ช่วยให้ครูสามารถค้นหาแบบฝึกหัดตัวเศษที่เหมาะสมสำหรับนักเรียนชั้นประถมศึกษาปีที่ 5 ได้อย่างแม่นยำผ่านความสามารถในการค้นหาและกรองที่มีประสิทธิภาพซึ่งสอดคล้องกับมาตรฐานหลักสูตร ครูสามารถปรับการสอนได้อย่างมีประสิทธิภาพโดยเลือกจากระดับความยากและประเภทของโจทย์ที่หลากหลาย ปรับแต่งแบบฝึกหัดให้ตรงกับความต้องการของนักเรียนแต่ละคนเพื่อการแก้ไขหรือเสริมความรู้ แพลตฟอร์มนี้มีความยืดหยุ่น ทำให้ครูสามารถใช้ทรัพยากรเหล่านี้ได้ทั้งในรูปแบบสิ่งพิมพ์และดิจิทัล รองรับสภาพแวดล้อมในห้องเรียนและวิธีการเรียนรู้ที่หลากหลาย แนวทางที่ครอบคลุมนี้ในการคัดสรรและปรับแต่งแบบฝึกหัดช่วยให้การวางแผนบทเรียนง่ายขึ้น ในขณะเดียวกันก็รับประกันว่านักเรียนจะได้รับการฝึกฝนที่ตรงเป้าหมายเกี่ยวกับแนวคิดเรื่องตัวเศษ ซึ่งท้ายที่สุดแล้วจะสร้างความเข้าใจพื้นฐานที่แข็งแกร่งซึ่งจำเป็นต่อความสำเร็จในการดำเนินการเศษส่วนขั้นสูงและการให้เหตุผลทางคณิตศาสตร์ที่ซับซ้อนยิ่งขึ้น
