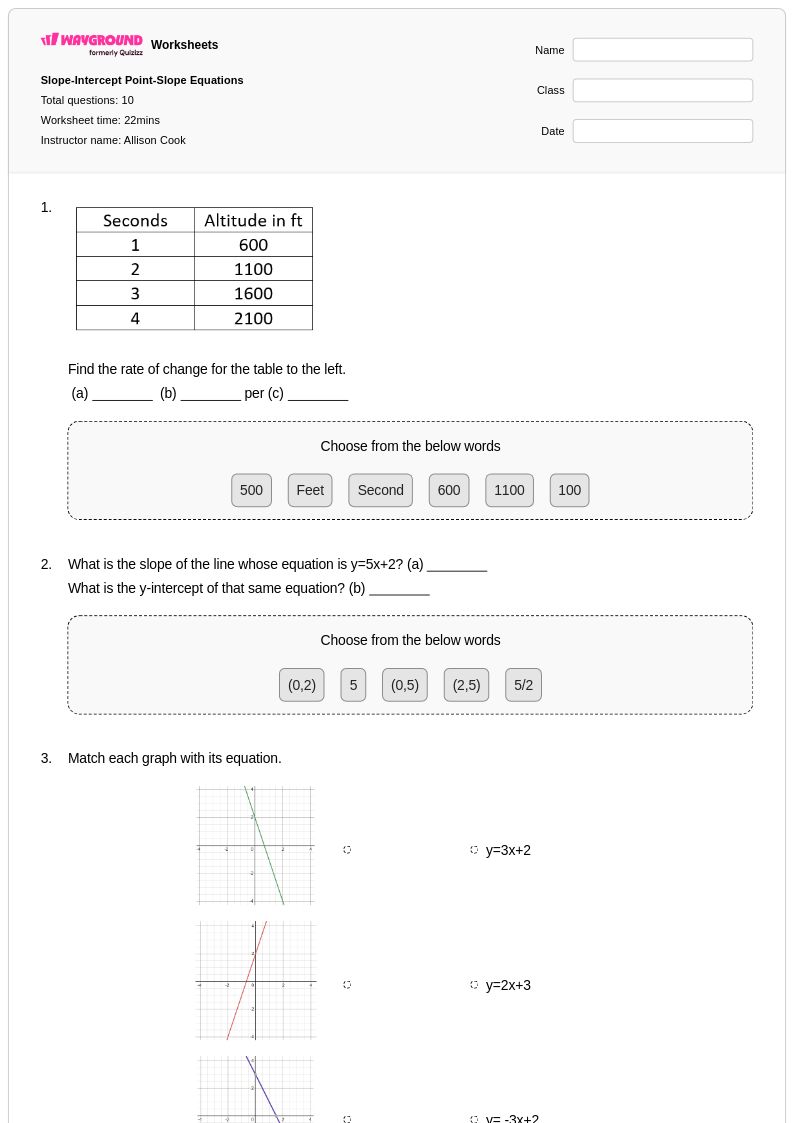
10 คิว
9th
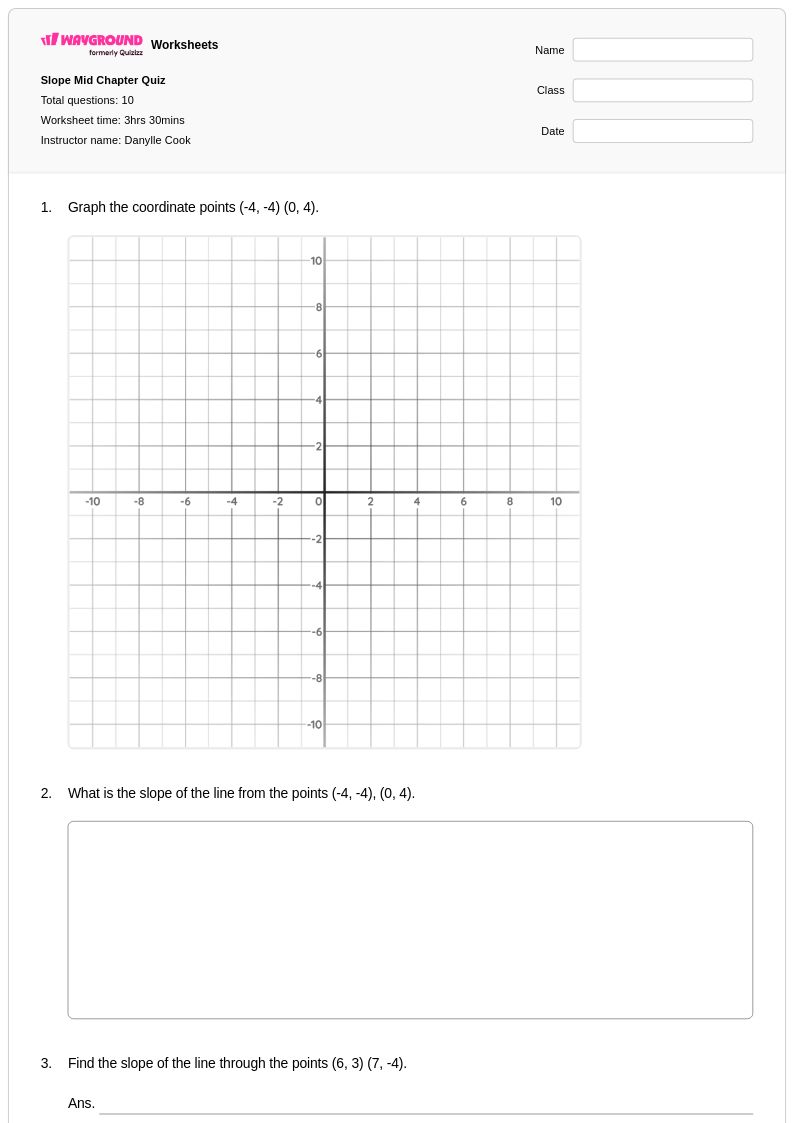
10 คิว
8th
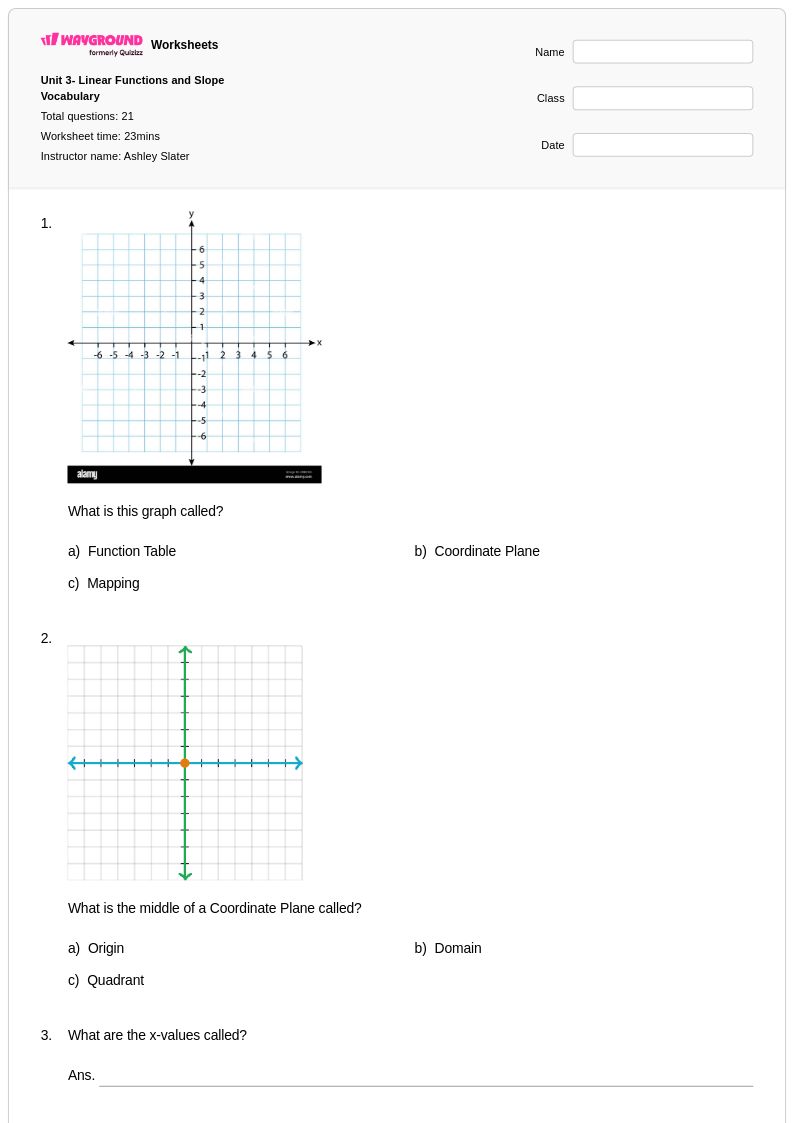
21 คิว
9th - 12th
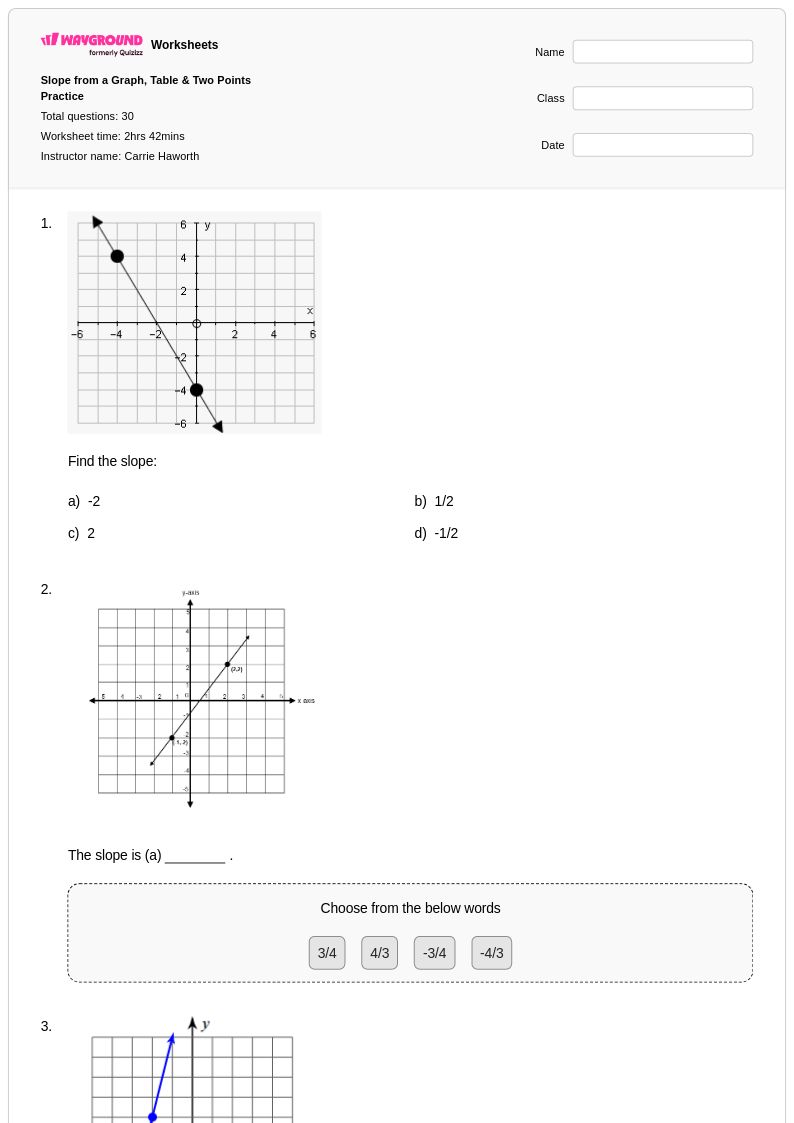
30 คิว
8th
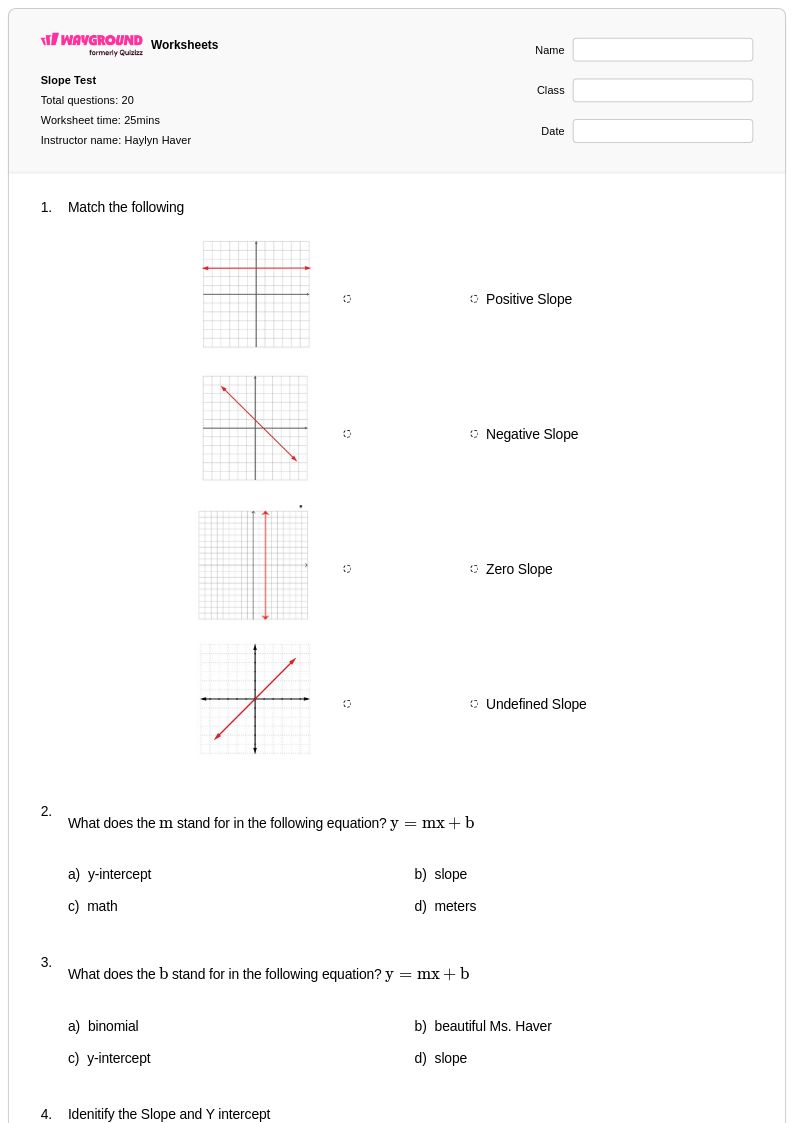
20 คิว
8th
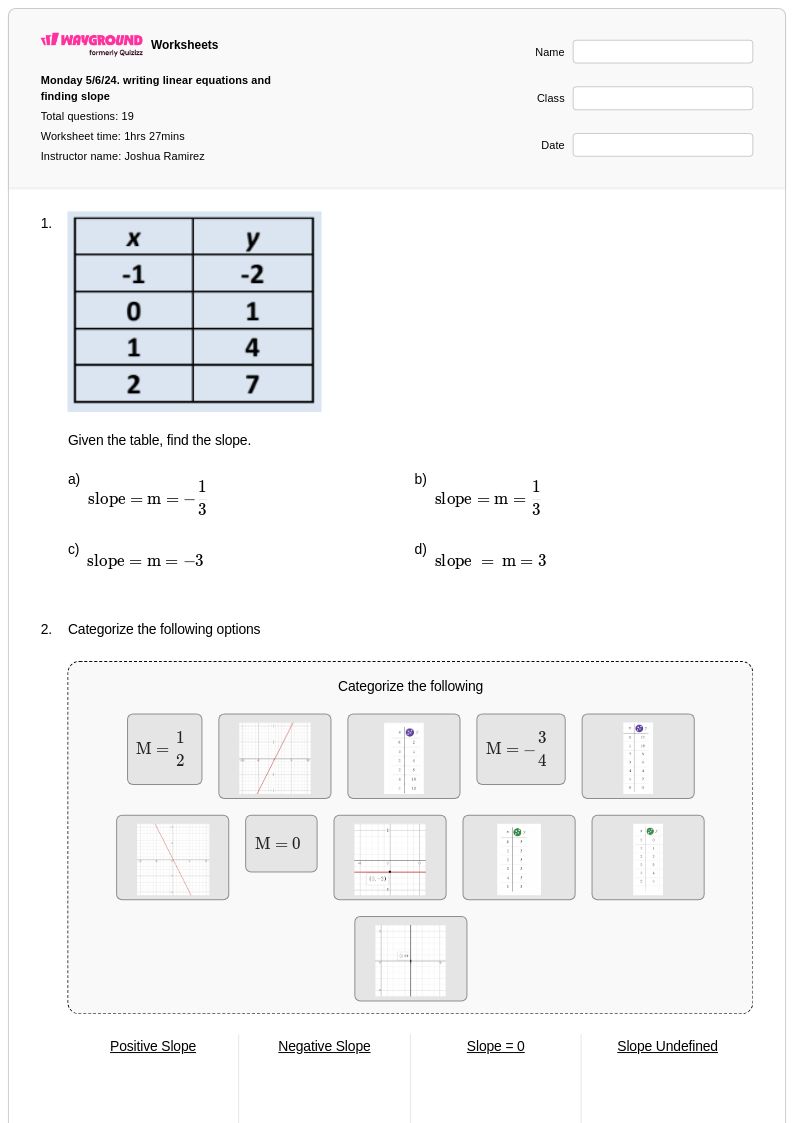
19 คิว
9th
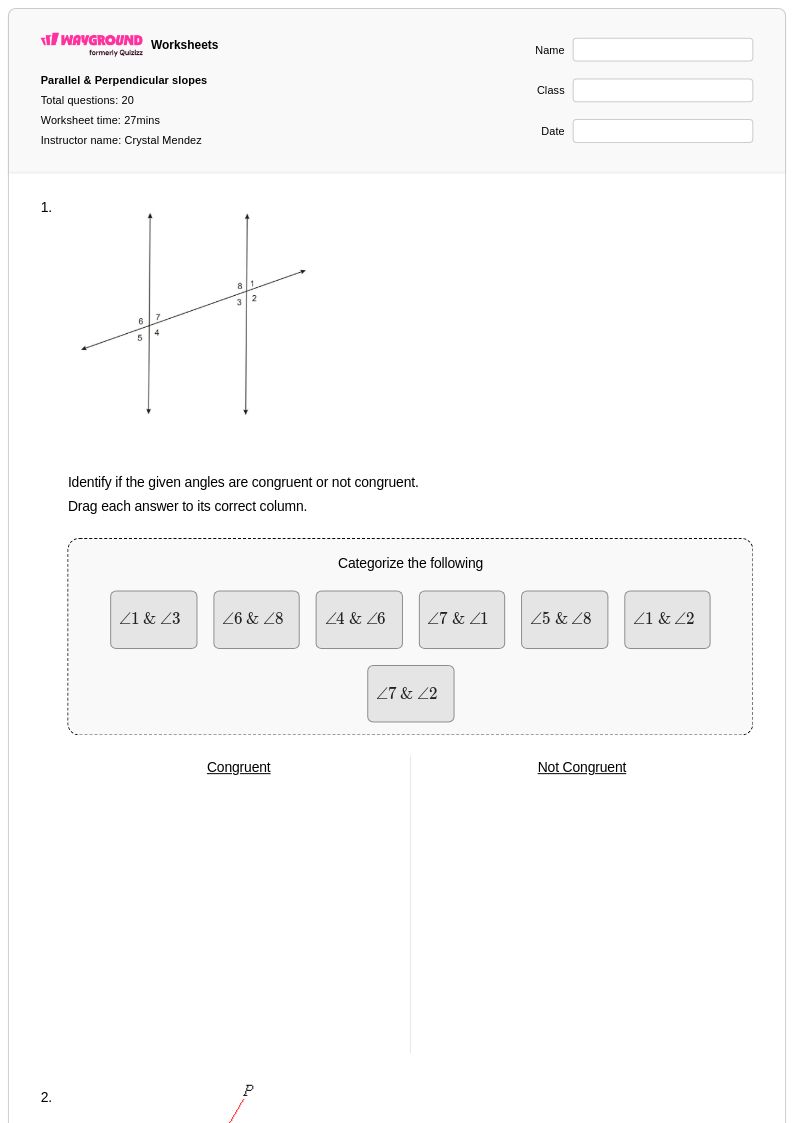
20 คิว
10th
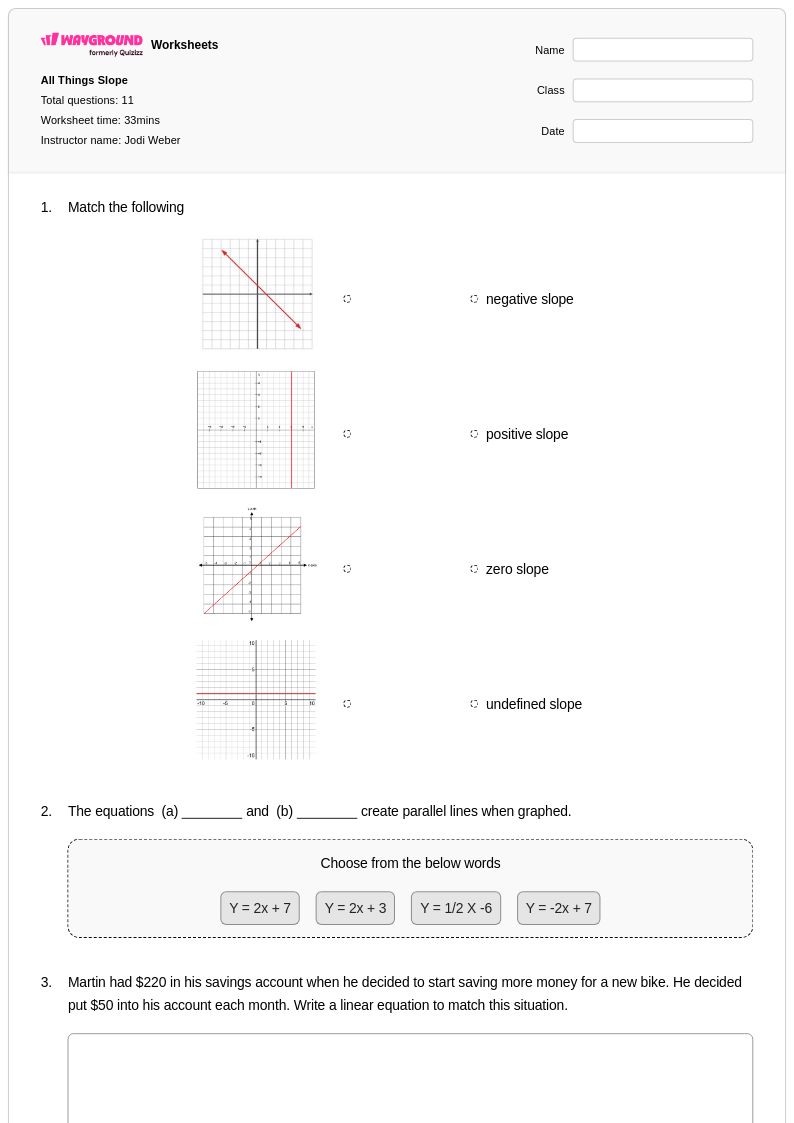
11 คิว
8th
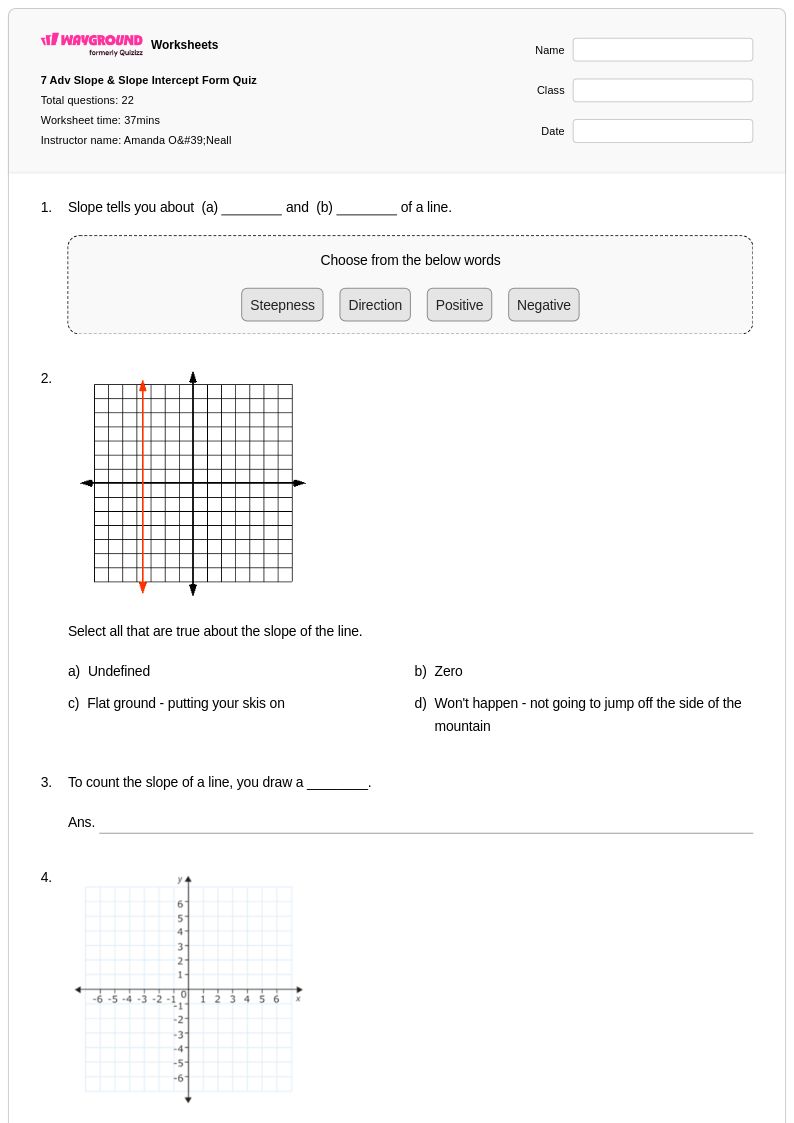
22 คิว
7th
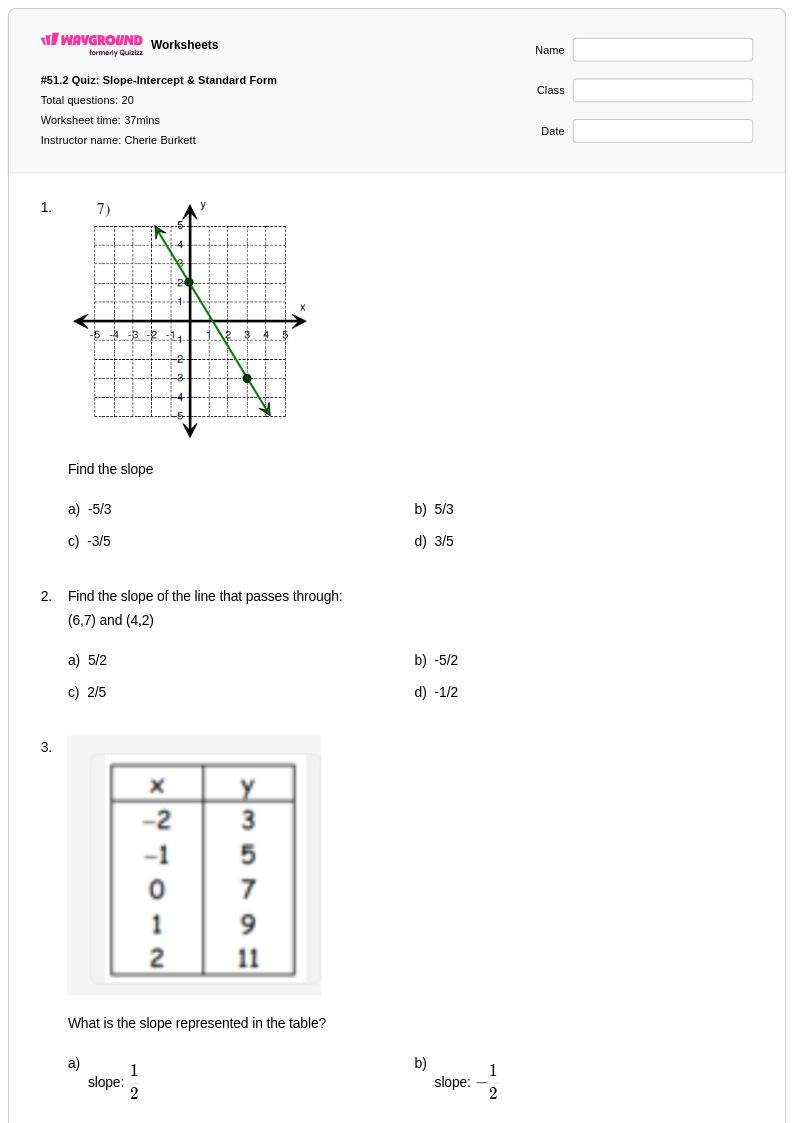
20 คิว
9th
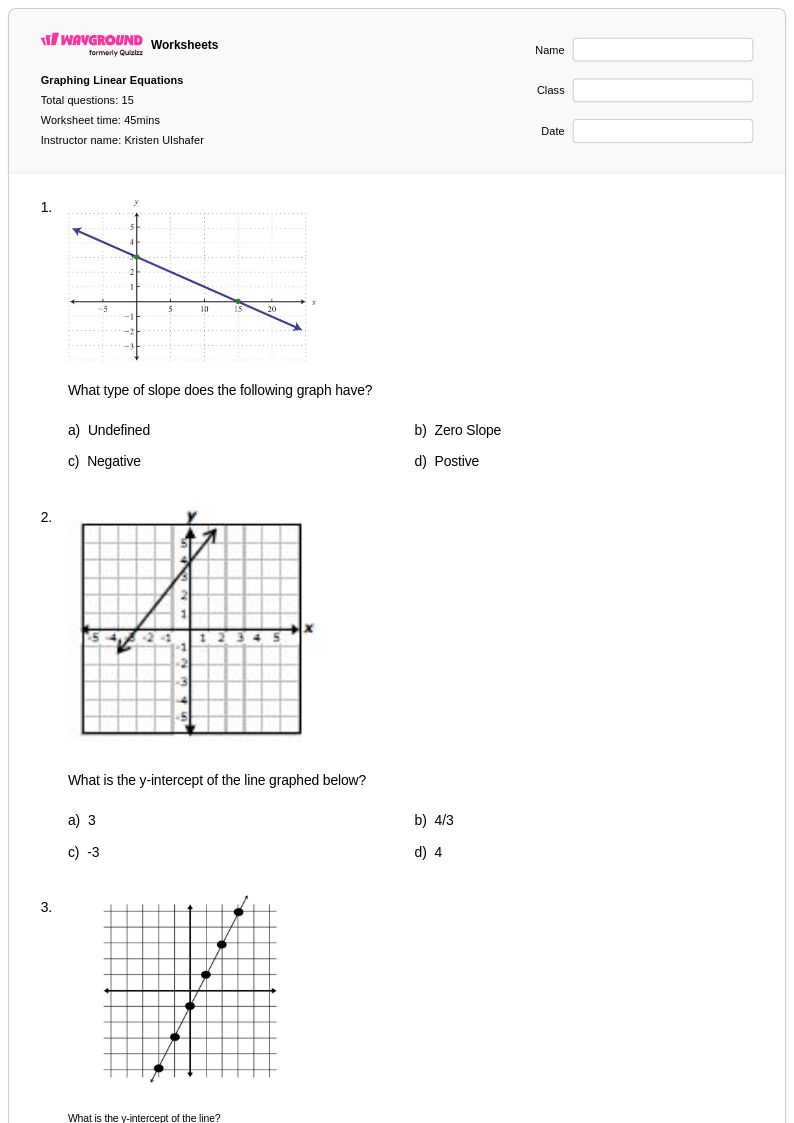
15 คิว
8th

14 คิว
12th
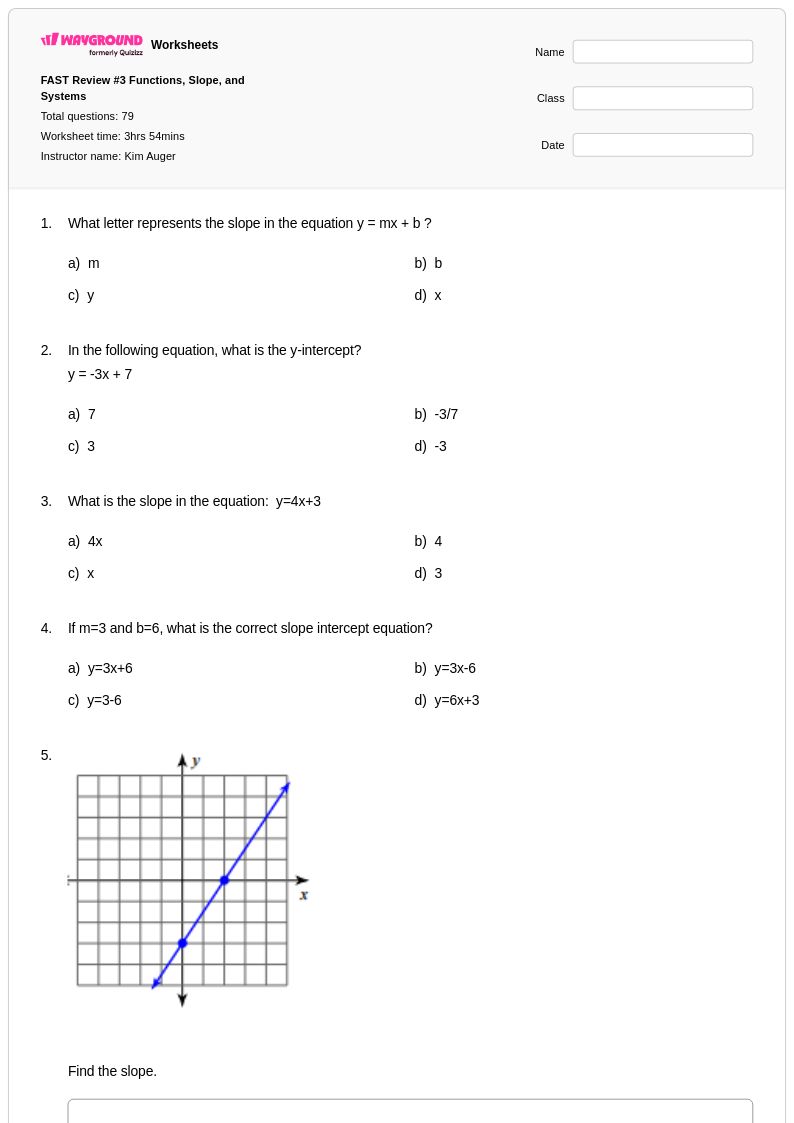
79 คิว
8th
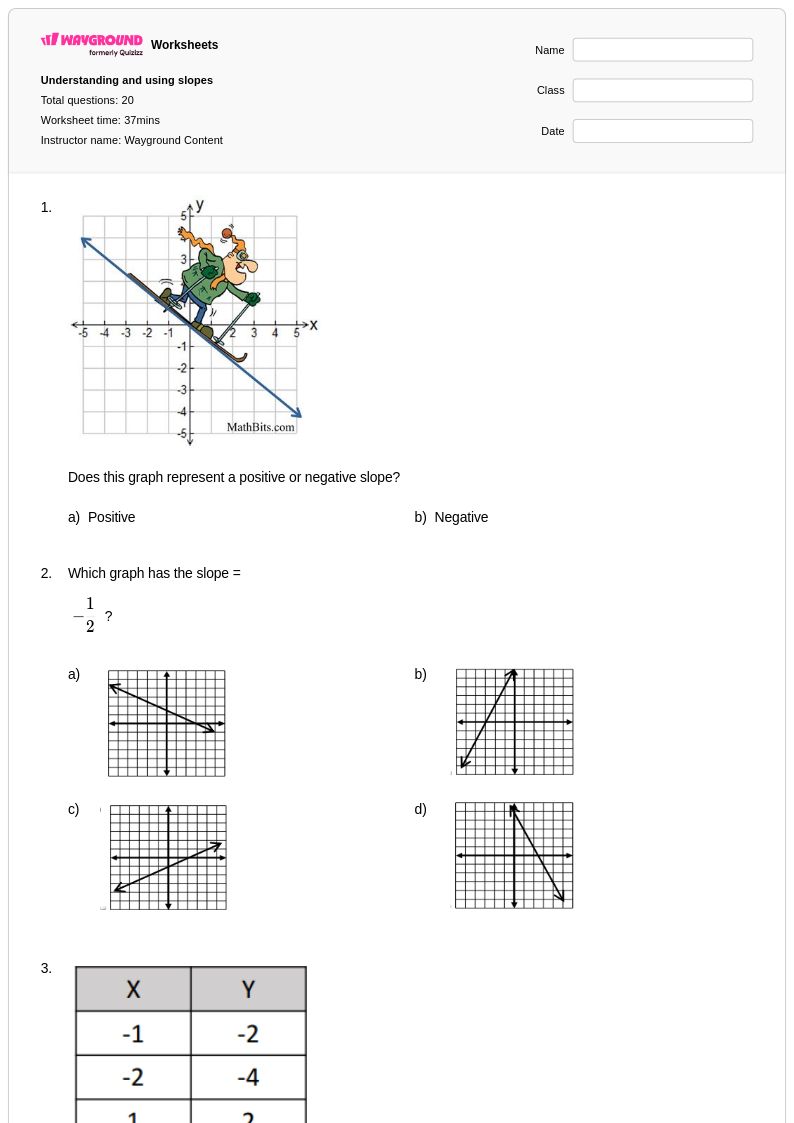
20 คิว
8th
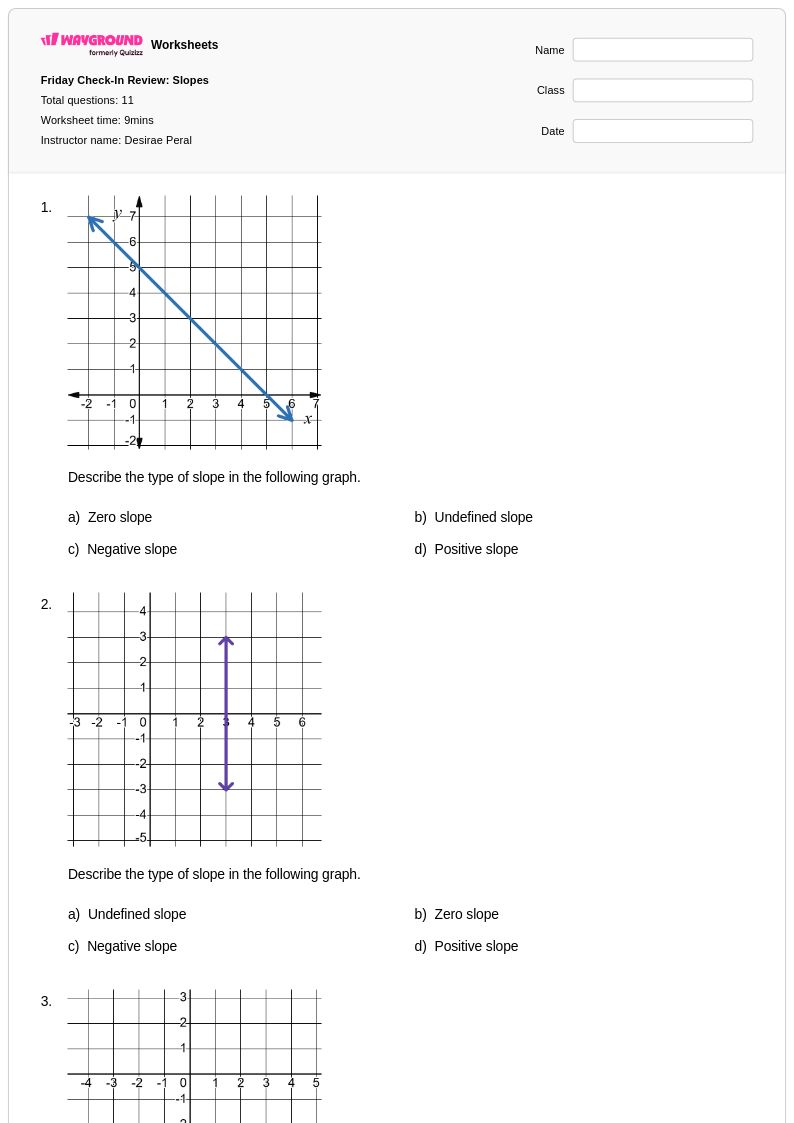
11 คิว
9th

10 คิว
8th
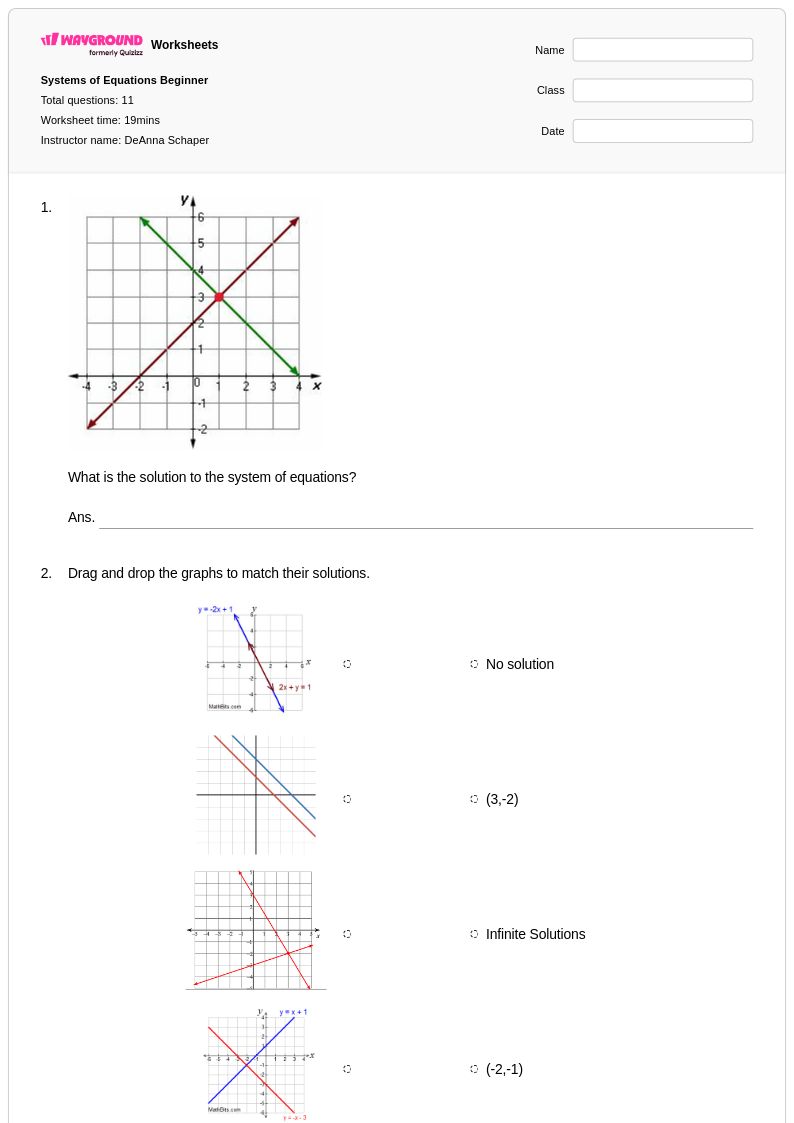
11 คิว
9th

17 คิว
8th

10 คิว
8th

21 คิว
9th - 12th
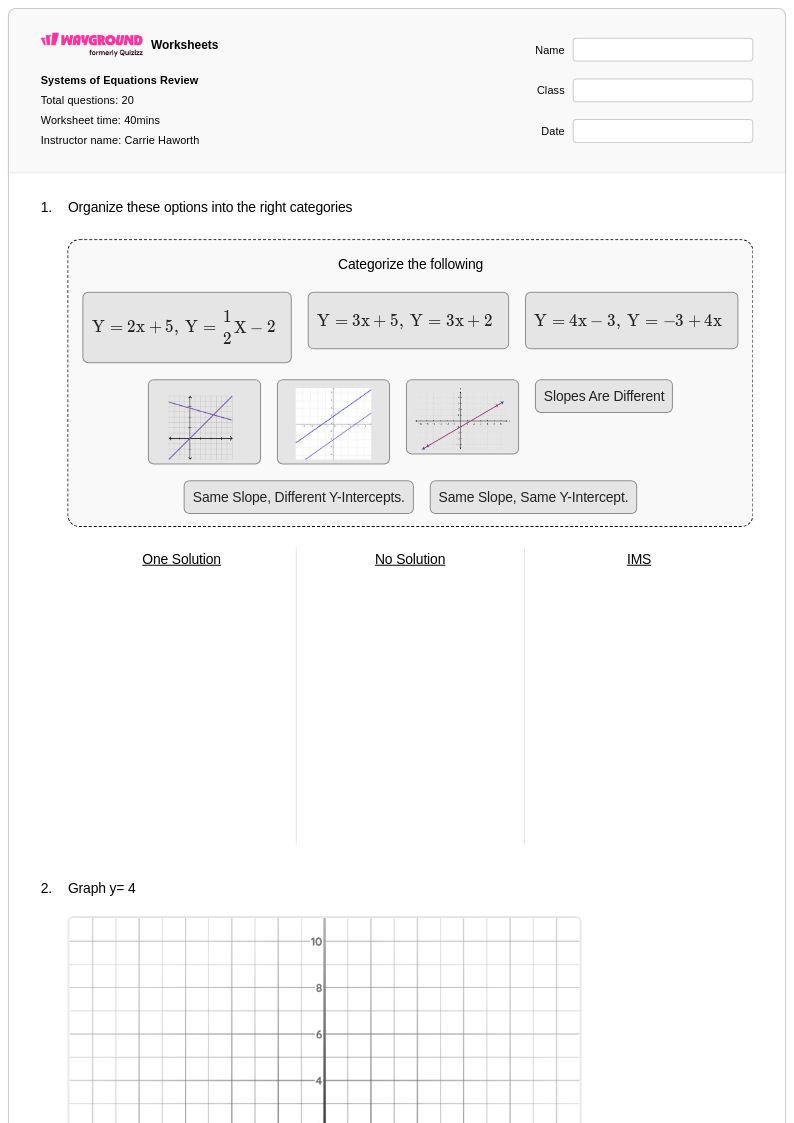
20 คิว
8th
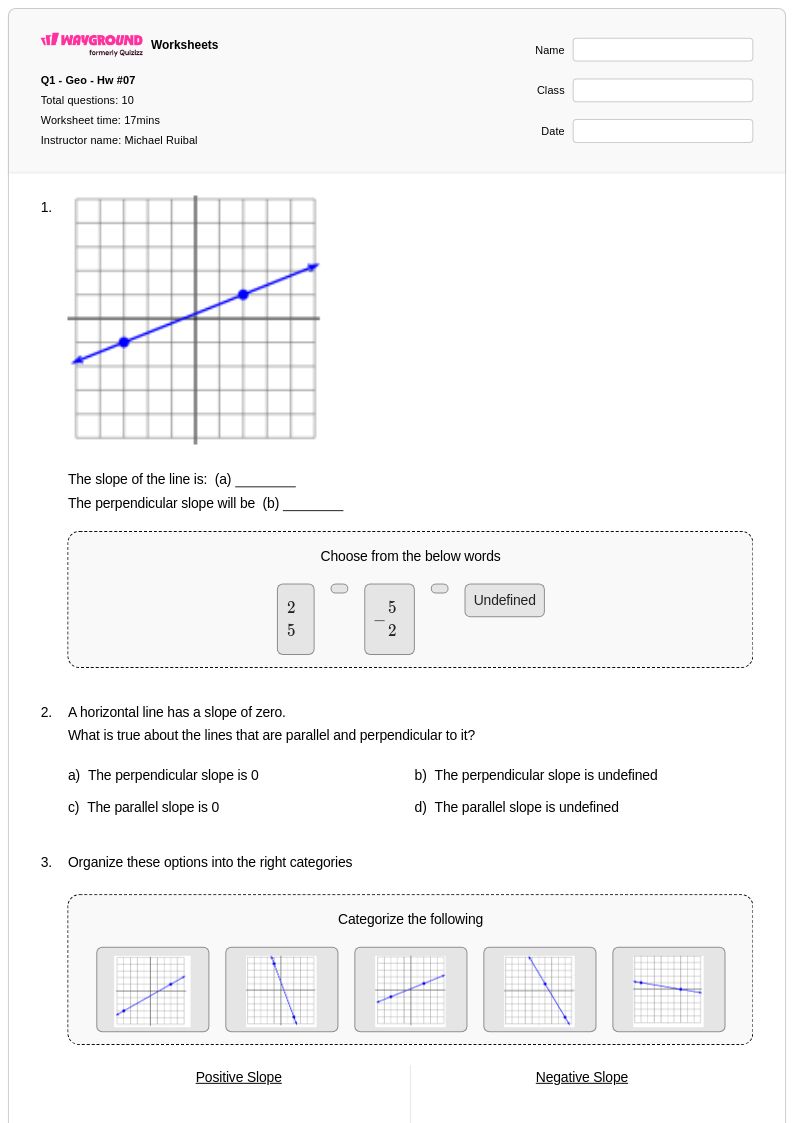
10 คิว
12th
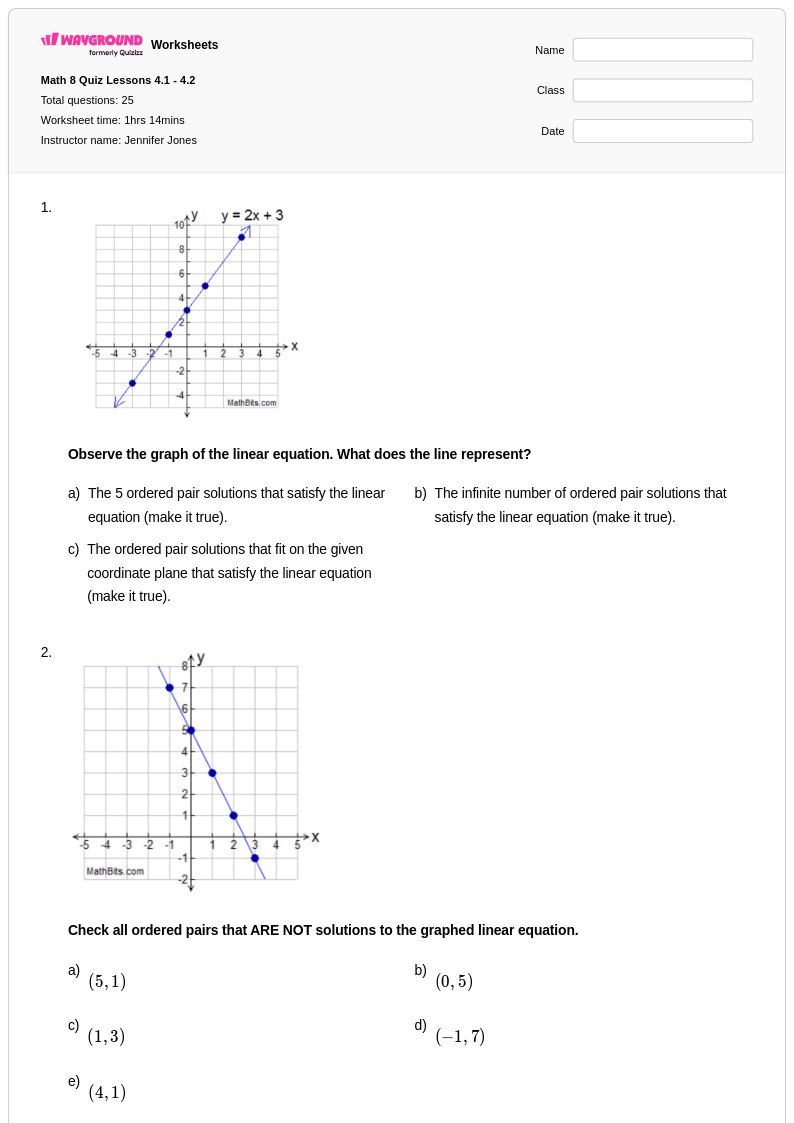
25 คิว
8th

6 คิว
7th
สำรวจแผ่นงานตามหัวเรื่อง
สำรวจแผ่นงาน สนามความลาดชัน ที่พิมพ์ได้
แบบฝึกหัดเรื่องสนามความชัน (Slope Field) จาก Wayground (เดิมคือ Quizizz) เป็นแบบฝึกหัดที่ครอบคลุมเกี่ยวกับแนวคิดที่เห็นภาพและเข้าใจง่ายที่สุดอย่างหนึ่งในวิชาแคลคูลัสสำหรับการทำความเข้าใจสมการเชิงอนุพันธ์ แบบฝึกหัดที่ออกแบบมาอย่างพิถีพิถันนี้จะแนะนำนักเรียนผ่านกระบวนการร่างสนามทิศทาง การตีความเส้นโค้งคำตอบ และการเชื่อมโยงการแสดงผลกราฟิกกับสมการเชิงอนุพันธ์พื้นฐาน นักเรียนจะพัฒนาทักษะการวิเคราะห์ที่สำคัญโดยการทำงานกับโจทย์ฝึกหัดที่หลากหลาย ตั้งแต่การสร้างสนามความชันขั้นพื้นฐานไปจนถึงการประยุกต์ใช้ขั้นสูงที่เกี่ยวข้องกับคำตอบสมดุลและภาพเฟส แบบฝึกหัดแต่ละชุดมีเฉลยคำตอบโดยละเอียดที่ช่วยให้นักเรียนตรวจสอบการตีความกราฟิกและเข้าใจความเข้าใจผิดทั่วไป ในขณะที่รูปแบบ PDF ที่พิมพ์ได้ฟรีช่วยให้เข้าถึงได้ทั้งสำหรับการเรียนการสอนในห้องเรียนและการศึกษาด้วยตนเอง
Wayground (เดิมคือ Quizizz) ช่วยเสริมศักยภาพให้กับครูผู้สอนคณิตศาสตร์ด้วยแหล่งข้อมูลสนามความชันนับล้านรายการที่สร้างโดยครูผู้สอน ซึ่งช่วยลดความยุ่งยากในการวางแผนบทเรียนและเพิ่มความเข้าใจของนักเรียนเกี่ยวกับสมการเชิงอนุพันธ์ แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานแคลคูลัสเฉพาะได้อย่างรวดเร็ว ไม่ว่าจะเป็นการเน้นที่ฟิลด์ทิศทางสำหรับสมการอิสระ หรือระบบที่ซับซ้อนกว่าอย่างระบบที่ไม่เป็นอิสระ เครื่องมือการปรับระดับความยากง่ายช่วยให้ผู้สอนสามารถปรับระดับความยากและประเภทของปัญหาให้เหมาะสมกับความต้องการในการเรียนรู้ที่หลากหลาย สนับสนุนทั้งการแก้ไขปัญหาสำหรับนักเรียนที่เรียนรู้ช้า และโอกาสในการเสริมสร้างความรู้สำหรับผู้เรียนที่มีความสามารถสูง แบบฝึกหัดเหล่านี้มีให้เลือกทั้งแบบพิมพ์ได้และแบบดิจิทัล รวมถึงไฟล์ PDF ที่ดาวน์โหลดได้ ช่วยให้สามารถนำไปใช้ได้อย่างยืดหยุ่นในสภาพแวดล้อมห้องเรียนแบบดั้งเดิมและห้องเรียนที่ใช้เทคโนโลยี ช่วยให้มั่นใจได้ว่านักเรียนจะได้รับการฝึกฝนทักษะที่ตรงเป้าหมาย ซึ่งช่วยเชื่อมช่องว่างระหว่างทฤษฎีสมการเชิงอนุพันธ์นามธรรมและการให้เหตุผลทางคณิตศาสตร์เชิงภาพ
