
21 Hỏi
2nd - Uni

10 Hỏi
6th

10 Hỏi
6th

9 Hỏi
6th
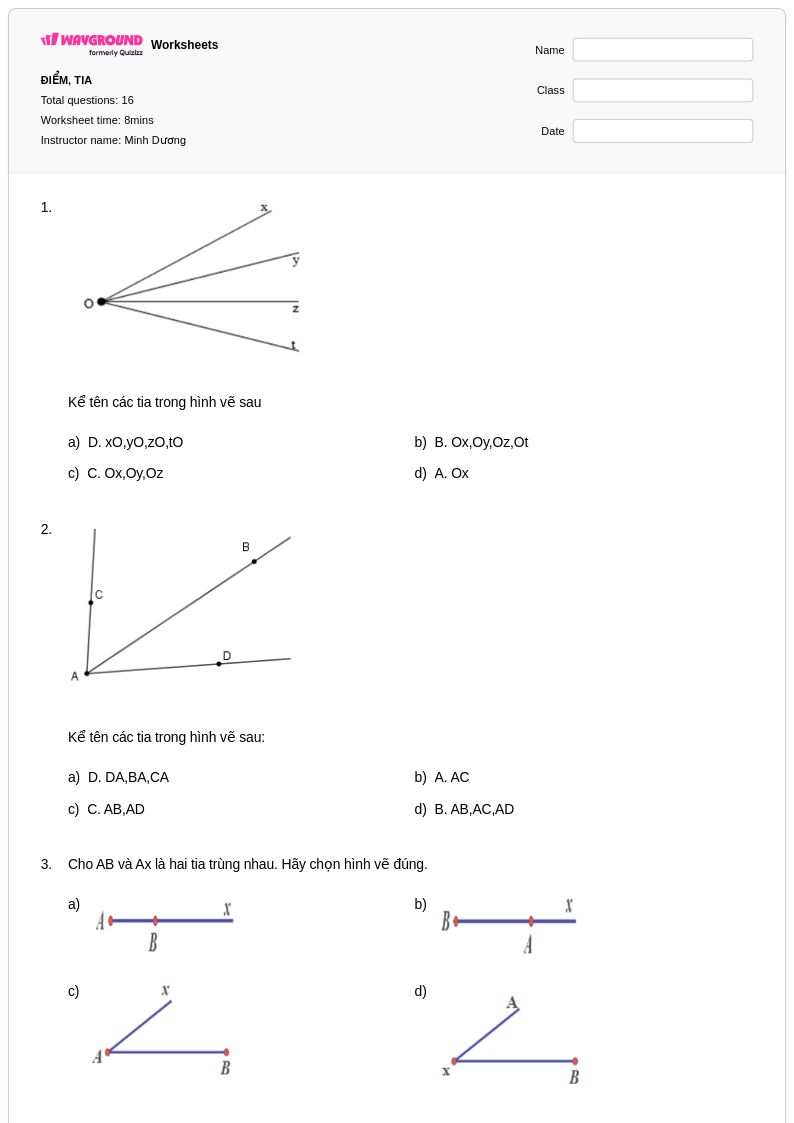
16 Hỏi
6th

10 Hỏi
6th

23 Hỏi
3rd - Uni

23 Hỏi
6th

24 Hỏi
KG - PD

7 Hỏi
6th

12 Hỏi
1st - 12th

10 Hỏi
6th

10 Hỏi
6th

10 Hỏi
6th

10 Hỏi
6th

10 Hỏi
6th

6 Hỏi
6th

10 Hỏi
6th

13 Hỏi
6th

10 Hỏi
6th
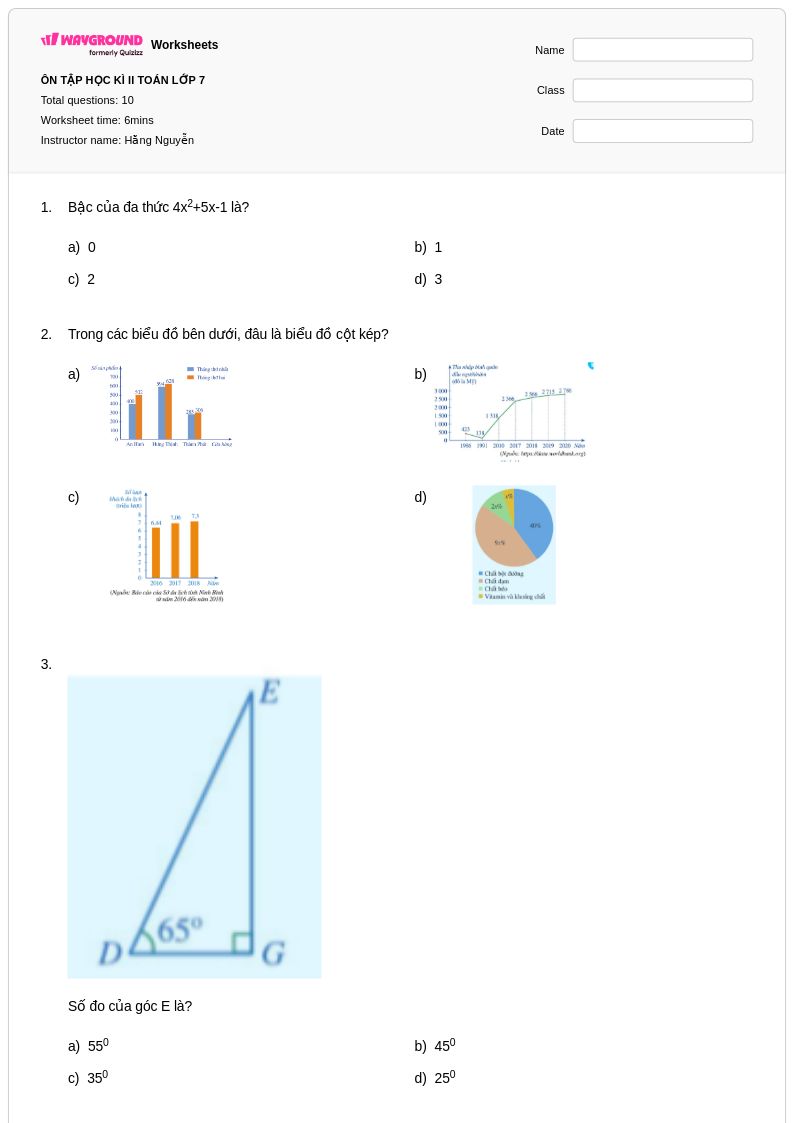
10 Hỏi
6th - 8th

8 Hỏi
6th

10 Hỏi
6th

10 Hỏi
6th
Khám phá các bảng tính chủ đề khác cho lớp 6
Khám phá các trang tính Suy luận quy nạp có thể in được cho Lớp 6
Các bài tập suy luận quy nạp dành cho học sinh lớp 6 có sẵn trên Wayground (trước đây là Quizizz) cung cấp bài tập thực hành thiết yếu để phát triển kỹ năng tư duy logic, nền tảng của các khái niệm đại số. Những tài liệu toàn diện này hướng dẫn học sinh lớp 6 thông qua quá trình quan sát các mẫu, đưa ra giả thuyết và rút ra kết luận tổng quát từ các ví dụ cụ thể—những kỹ năng quan trọng chuẩn bị cho các em tư duy toán học nâng cao hơn. Các bài tập thực hành xây dựng một cách có hệ thống khả năng của học sinh trong việc xác định các mẫu số, dãy số hình học và các mối quan hệ đại số, đồng thời củng cố khả năng diễn đạt tư duy toán học của các em. Mỗi bài tập đều bao gồm đáp án chi tiết hỗ trợ cả việc tự học và giảng dạy trên lớp, với định dạng PDF có thể in miễn phí, đảm bảo khả năng tiếp cận cho nhiều môi trường học tập khác nhau.
Wayground (trước đây là Quizizz) cung cấp cho các nhà giáo dục hàng triệu tài nguyên suy luận quy nạp do giáo viên tạo ra, được thiết kế đặc biệt cho việc giảng dạy toán học lớp 6. Khả năng tìm kiếm và lọc mạnh mẽ của nền tảng cho phép giáo viên nhanh chóng tìm thấy các bài tập phù hợp với tiêu chuẩn chương trình giảng dạy, đồng thời sử dụng các công cụ phân hóa để đáp ứng nhu cầu đa dạng của học sinh. Các tùy chọn tùy chỉnh linh hoạt cho phép các nhà giáo dục sửa đổi các tài liệu hiện có hoặc tạo các bộ bài tập thực hành có mục tiêu cho các hoạt động bổ trợ và nâng cao. Có sẵn cả ở dạng in và kỹ thuật số, bao gồm cả các tệp PDF có thể tải xuống, các tài liệu này giúp đơn giản hóa việc lập kế hoạch bài học đồng thời cung cấp nhiều phương pháp thực hành kỹ năng, cho dù học sinh đang nỗ lực để nắm vững khả năng nhận diện mẫu cơ bản hay mở rộng hiểu biết của mình sang các thử thách tư duy đại số phức tạp hơn.
