Understanding Definite Integrals and Area Calculation

The video tutorial explains how to find the area of a shaded region using a definite integral. It begins by introducing the concept of definite integrals for continuous and nonnegative functions over a closed interval. The tutorial identifies the interval and the linear function, then calculates the slope and forms the equation of the line. It proceeds to calculate the area of the shaded region, which is a trapezoid, using the area formula. Finally, the video summarizes the process and confirms the area calculation as 20.

What is the condition for using a definite integral to find the area under a function?

• The function must be continuous and nonnegative.

• The function must be linear.

• The function must be quadratic.

• The function must be discontinuous.

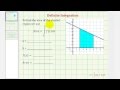
What are the values of 'A' and 'B' for the definite integral in this problem?

• A = 3, B = 7

• A = 1, B = 5

• A = 2, B = 6

• A = 0, B = 10

What is the y-intercept of the linear function used in this problem?

• 5

• 6

• 7

• 8

Tags

CCSS.8.EE.B.5

How is the slope of the linear function determined?

• By using the quadratic formula.

• By calculating the area under the curve.

• By finding the change in y over the change in x.

• By using the midpoint formula.

Tags

CCSS.8.F.B.4

CCSS.HSF.LE.A.2

What is the equation of the linear function derived in the video?

• f(x) = x + 7

• f(x) = -1/2x + 7

• f(x) = 2x + 5

• f(x) = -x + 6

Tags

CCSS.6.G.A.1

What shape is the shaded region whose area is being calculated?

• Rectangle

• Circle

• Trapezoid

• Triangle

What are the lengths of the two bases of the trapezoid?

• 6 units and 4 units

• 5 units and 3 units

• 7 units and 2 units

• 8 units and 1 unit

Tags

CCSS.6.G.A.1

What is the height of the trapezoid used in the area calculation?

• 3 units

• 6 units

• 5 units

• 4 units

What is the final calculated area of the shaded region?

• 18

• 20

• 22

• 15

What is the definite integral of the function from 2 to 6?

• 18

• 15

• 22

• 20