Temas recomendados para ti
- Kąt depresji
- Kąt elewacji i depresji
- Twierdzenie odwrotne Pitagorasa
- Funkcja cosekans
- Cotangens
- Tożsamości podwójne i połówkowe kąta
- Tożsamości podwójnego kąta
- Wykres sinusa i cosinusa
- Odwrotne funkcje trygonometryczne
- Odwrotne stosunki trygonometryczne
- Prawo cosinusów
- Prawo sinusów
- Tożsamości pitagorejskie
- Twierdzenie Pitagorasa
- Miara radianowa
- Radiany i długość łuku
- Radiany i stopnie
- Kąt odniesienia
- Zadania tekstowe dotyczące trójkąta prostokątnego
- Równania sinusów i cosinusów
- Wykresy sinusów i cosinusów
- Prawo sinusoidalne – przypadek niejednoznaczny
- Współczynnik sinusoidalny
- Tożsamości sum i różnic
- Funkcja tangensowa
- Równania trygonometryczne
- Funkcje trygonometryczne
- Wykresy trygonometryczne
- Tożsamości trygonometryczne
- Dowody tożsamości trygonometrycznej
- Dowody trygonometryczne
- Stosunki trygonometryczne Sin, Cos, Tan, Csc, Sec i Cot
- Koło jednostkowe
7Q
10th - 12th
11Q
9th - 12th

16Q
9th - 12th
19Q
9th - 12th

10Q
9th - Uni

15Q
11th
21Q
11th

16Q
11th
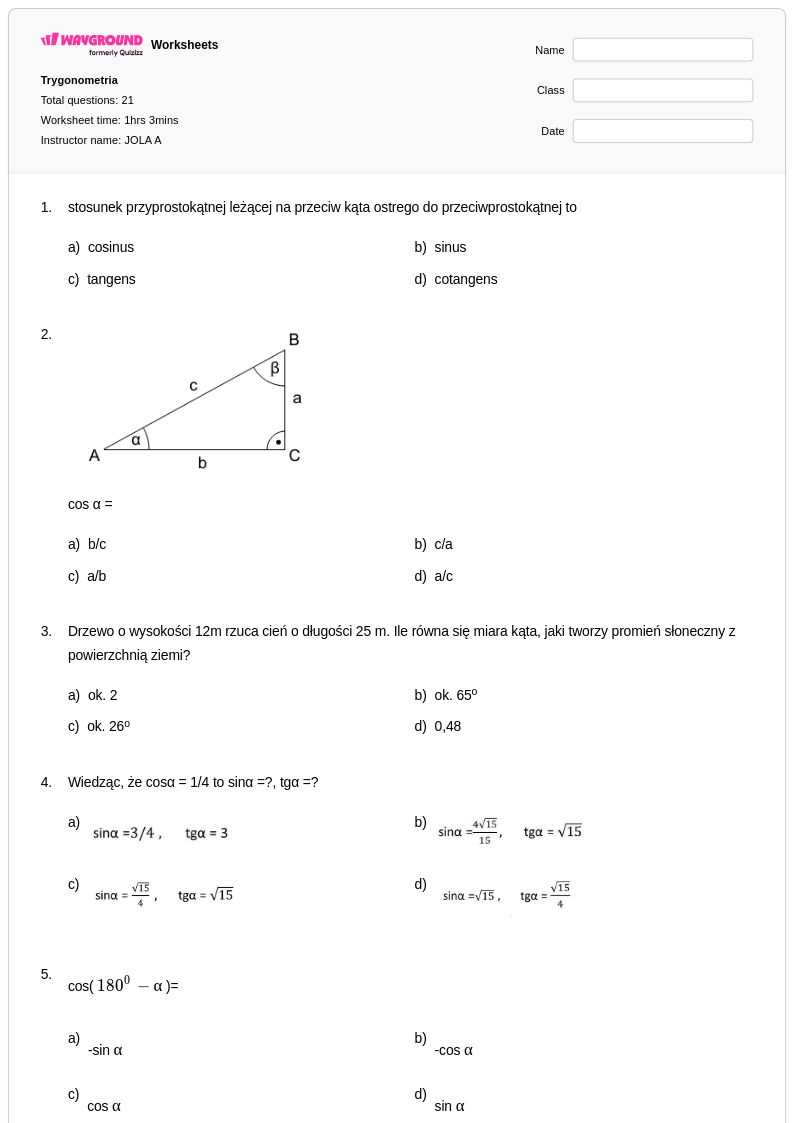
21Q
11th

21Q
11th
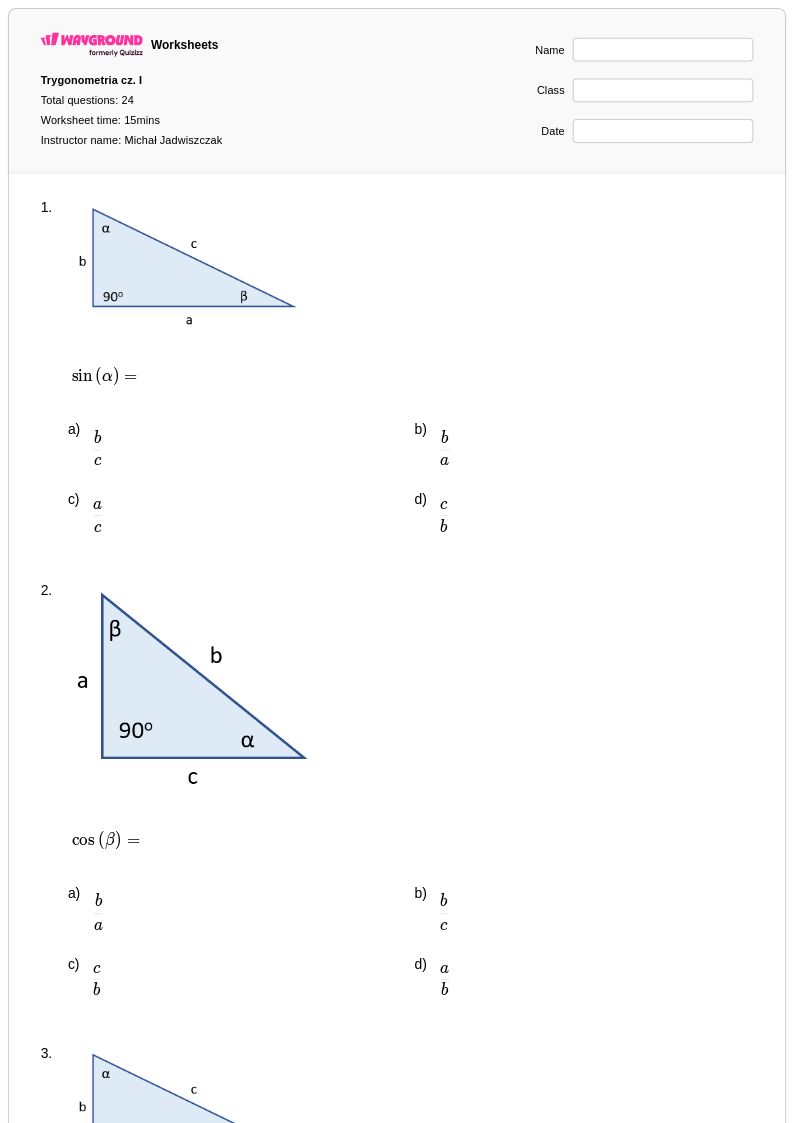
24Q
6th - 12th

11Q
10th - 12th

9Q
10th - 12th
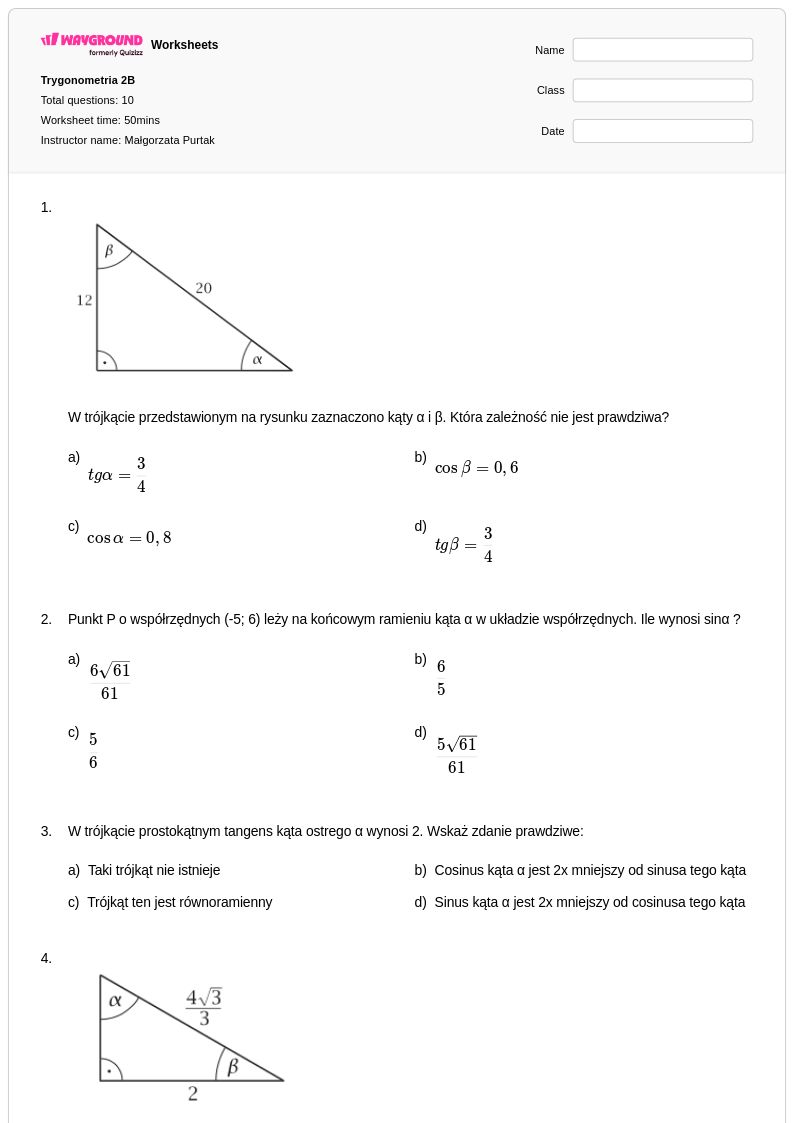
10Q
9th - 11th

8Q
9th - 12th

10Q
11th

10Q
9th - 12th
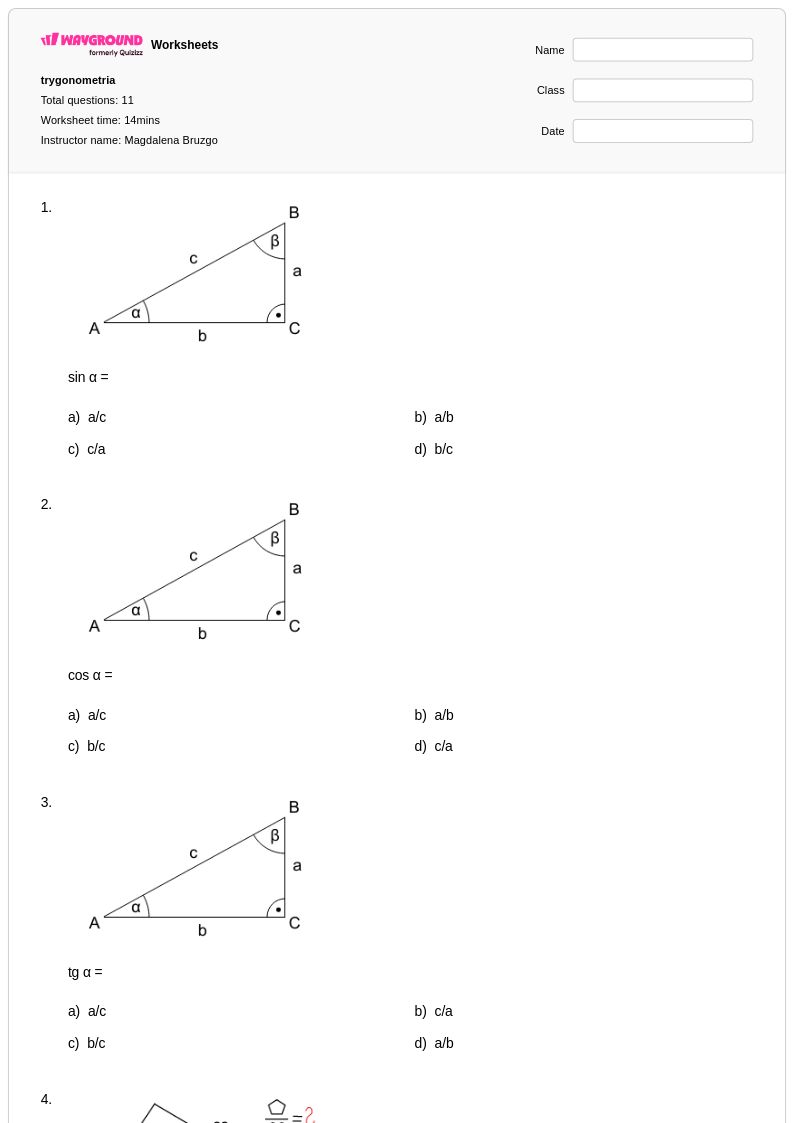
11Q
4th - 12th
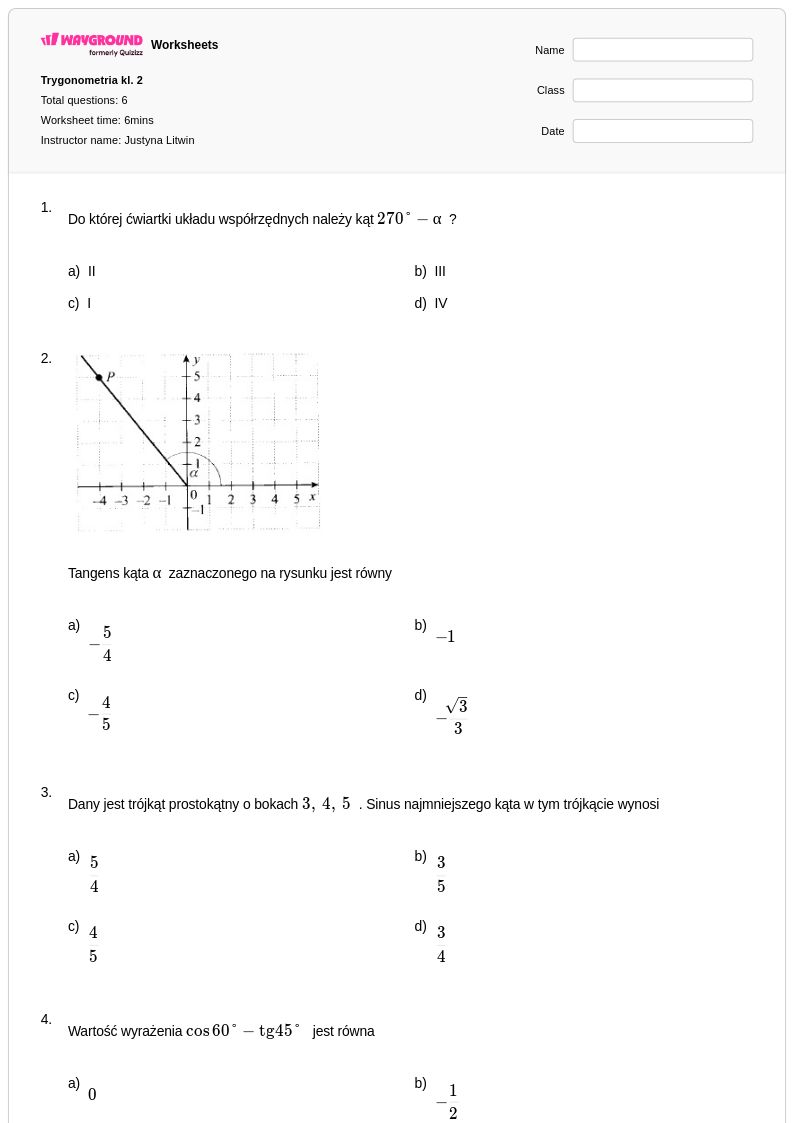
6Q
11th

23Q
KG - PD
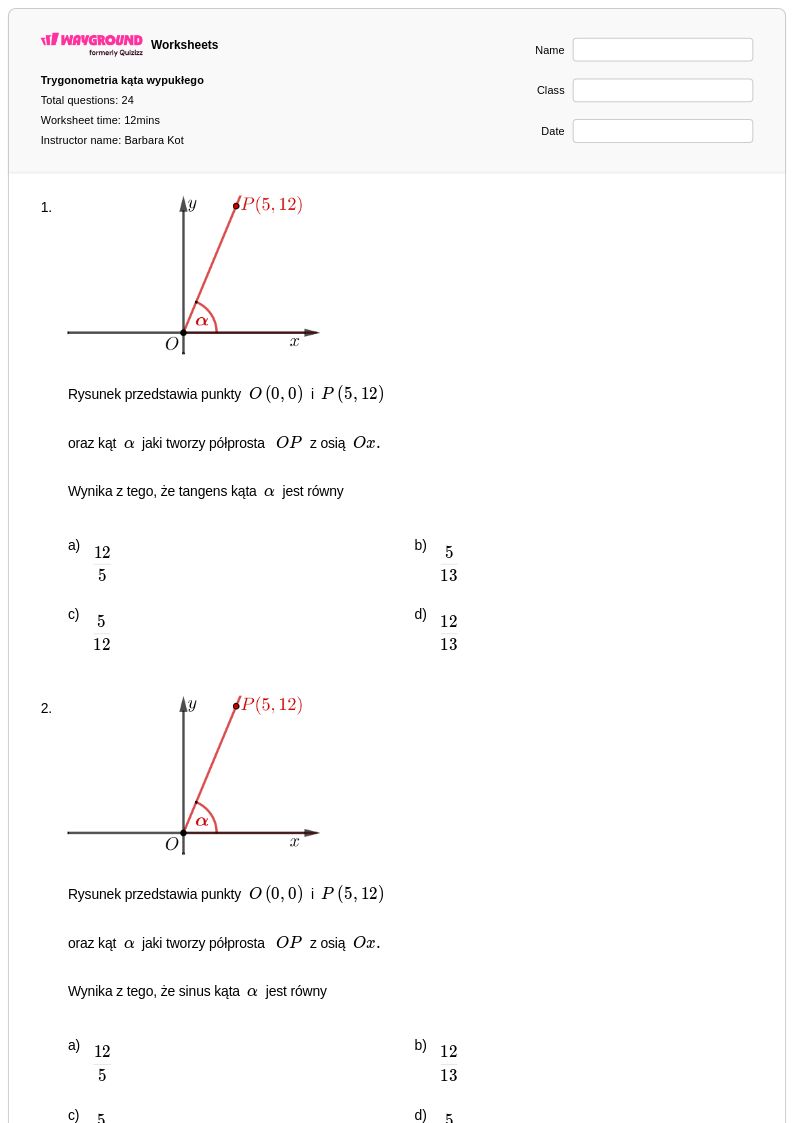
24Q
9th - 12th
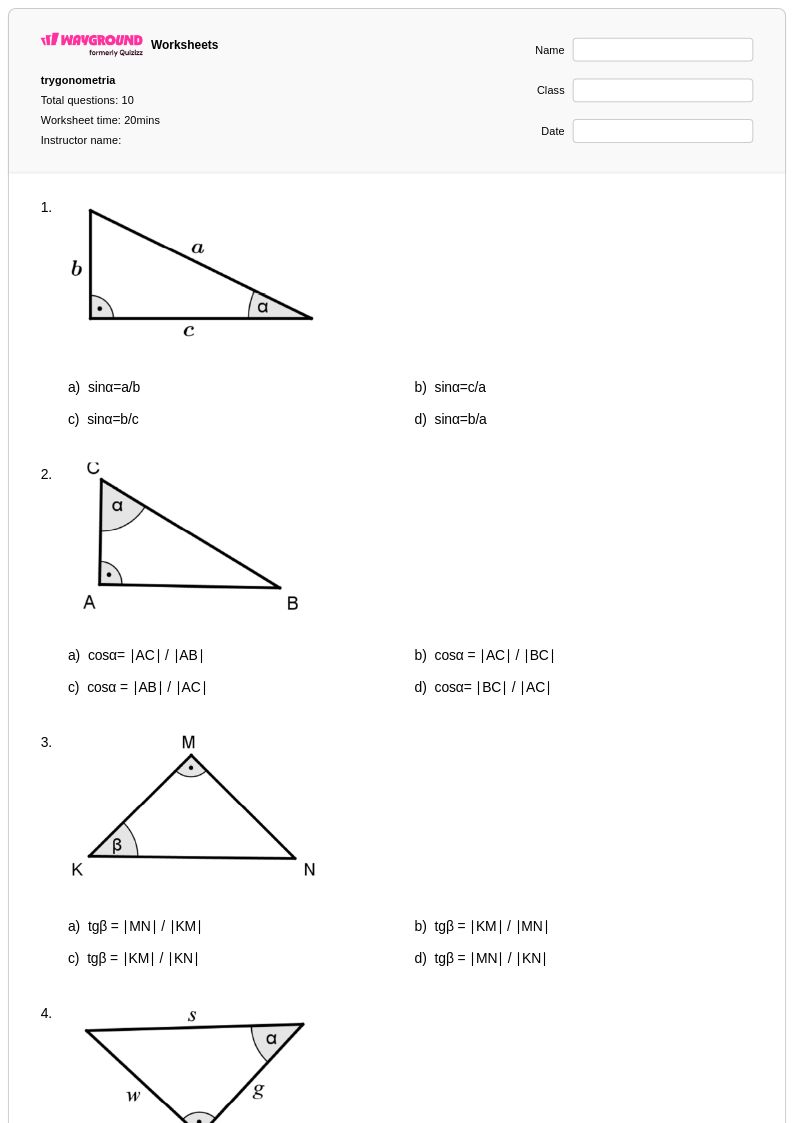
10Q
9th - 12th
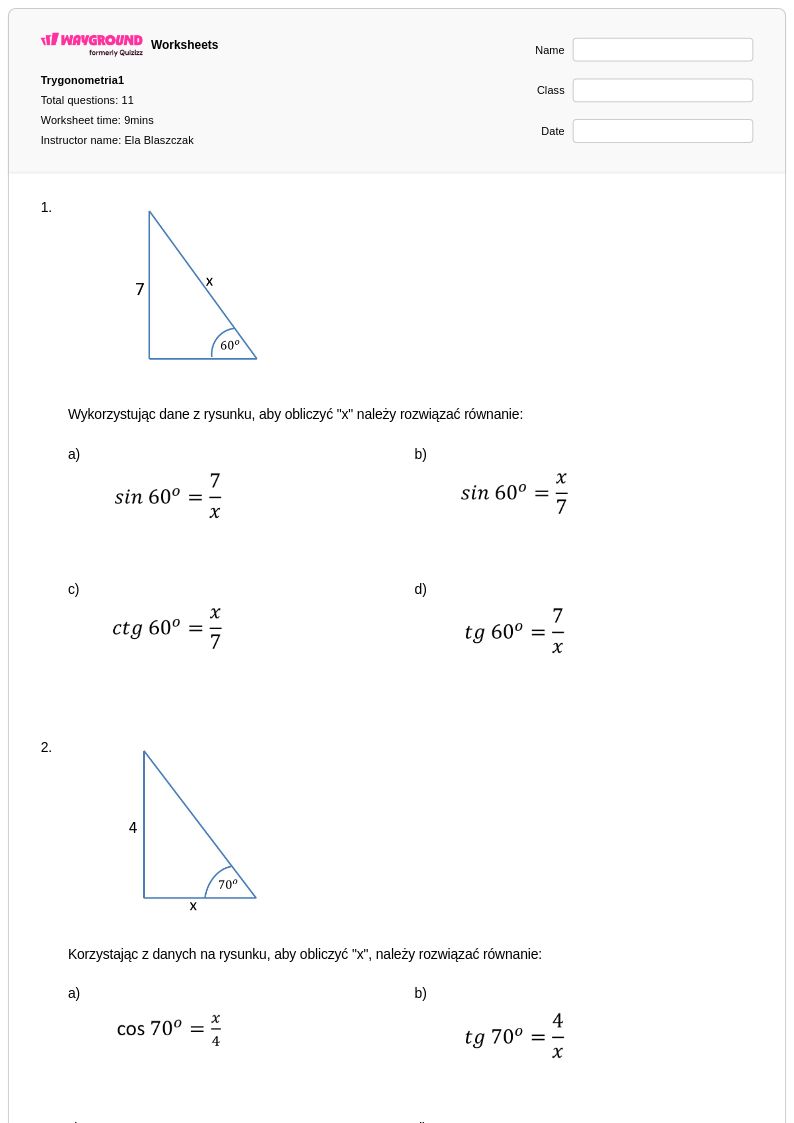
11Q
10th - 12th
20Q
11th
Explorar Trygonometria hojas de trabajo por grados
Explorar Trygonometria Hojas de trabajo para klasa 11 por Tema
- Kąt depresji
- Kąt elewacji i depresji
- Twierdzenie odwrotne Pitagorasa
- Funkcja cosekans
- Cotangens
- Tożsamości podwójne i połówkowe kąta
- Tożsamości podwójnego kąta
- Wykres sinusa i cosinusa
- Odwrotne funkcje trygonometryczne
- Odwrotne stosunki trygonometryczne
- Prawo cosinusów
- Prawo sinusów
- Tożsamości pitagorejskie
- Twierdzenie Pitagorasa
- Miara radianowa
- Radiany i długość łuku
- Radiany i stopnie
- Kąt odniesienia
- Zadania tekstowe dotyczące trójkąta prostokątnego
- Równania sinusów i cosinusów
Explore otras hojas de trabajo de materias para klasa 11
Przeglądaj arkusze Trygonometria do wydrukowania dla Klasa 11
Karty pracy z trygonometrii dla uczniów klasy 11, dostępne w Wayground (dawniej Quizizz), zapewniają kompleksowe ćwiczenia z podstawowymi pojęciami, takimi jak sinus, cosinus i tangens, tożsamości trygonometryczne, zależności między okręgami jednostkowymi oraz zaawansowane zastosowania w rozwiązywaniu problemów praktycznych. Te starannie zaprojektowane karty pracy wzmacniają umiejętności uczniów w zakresie analizowania funkcji okresowych, rozwiązywania równań trygonometrycznych, pracy z odwrotnymi funkcjami trygonometrycznymi oraz stosowania twierdzenia sinusów i cosinusów do złożonych problemów geometrycznych. Każdy zbiór kart pracy zawiera szczegółowe klucze odpowiedzi, które wspierają samodzielną naukę i samoocenę, a darmowy format do druku zapewnia dostępność dla wszystkich uczniów. Zadania praktyczne systematycznie przechodzą od podstawowych zależności między kątami do zaawansowanych zastosowań obejmujących modelowanie i analizę trygonometryczną, pomagając uczniom budować pewność siebie i biegłość w tej trudnej dziedzinie matematyki.
Wayground (dawniej Quizizz) oferuje nauczycielom dostęp do milionów zasobów trygonometrycznych stworzonych przez nauczycieli, dostosowanych do standardów matematyki dla klasy 11., oferując rozbudowane funkcje wyszukiwania i filtrowania, które pozwalają nauczycielom na lokalizowanie materiałów według konkretnych celów nauczania, poziomów trudności lub pojęć trygonometrycznych. Narzędzia różnicujące dostępne na platformie umożliwiają nauczycielom dostosowywanie arkuszy ćwiczeń do zróżnicowanych potrzeb edukacyjnych, zapewniając zarówno wsparcie w zakresie korepetycji dla uczniów mających trudności, jak i możliwości wzbogacenia wiedzy dla uczniów zaawansowanych. Te elastyczne zasoby są dostępne zarówno w formacie PDF do druku, jak i w interaktywnych wersjach cyfrowych, usprawniając planowanie lekcji i wspierając zróżnicowane metody nauczania, od tradycyjnych zadań domowych po wspólne zajęcia w klasie. Obszerny zbiór ułatwia ukierunkowane ćwiczenie umiejętności w takich obszarach, jak wykresy funkcji trygonometrycznych, rozwiązywanie zadań aplikacyjnych oraz rozwijanie biegłości proceduralnej w zakresie przekształceń i tożsamości trygonometrycznych.
