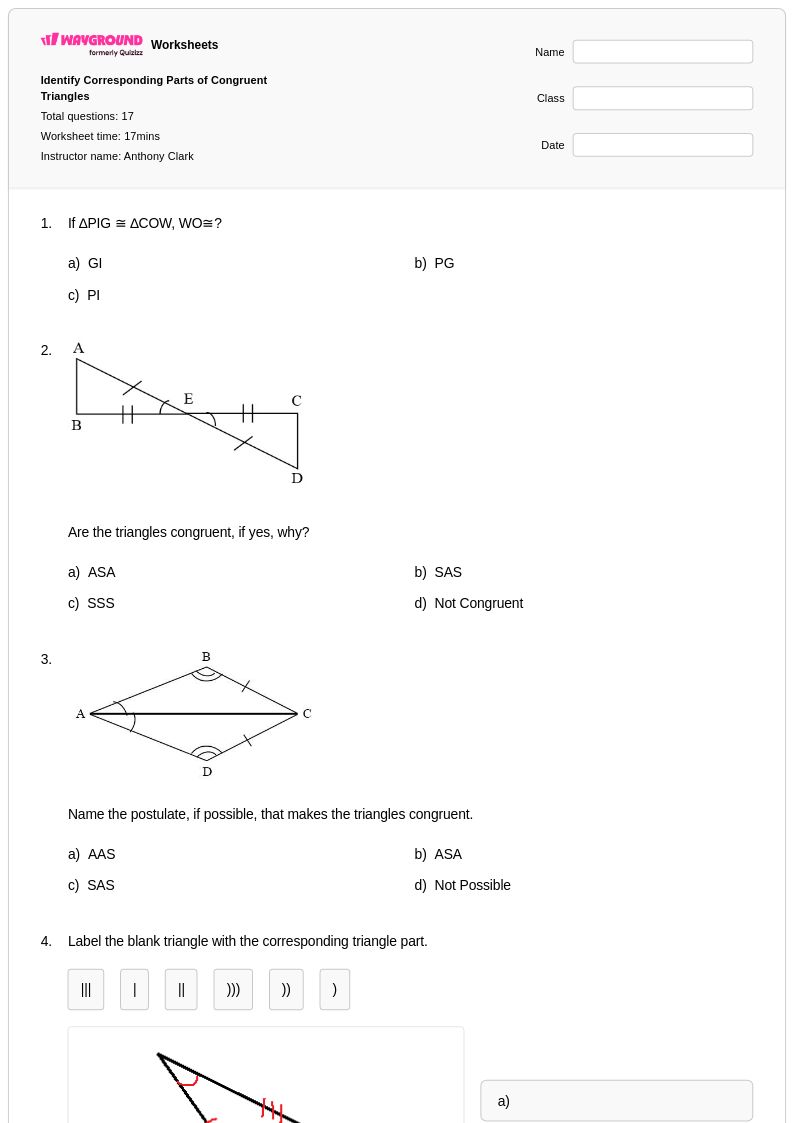
17 คิว
10th - Uni
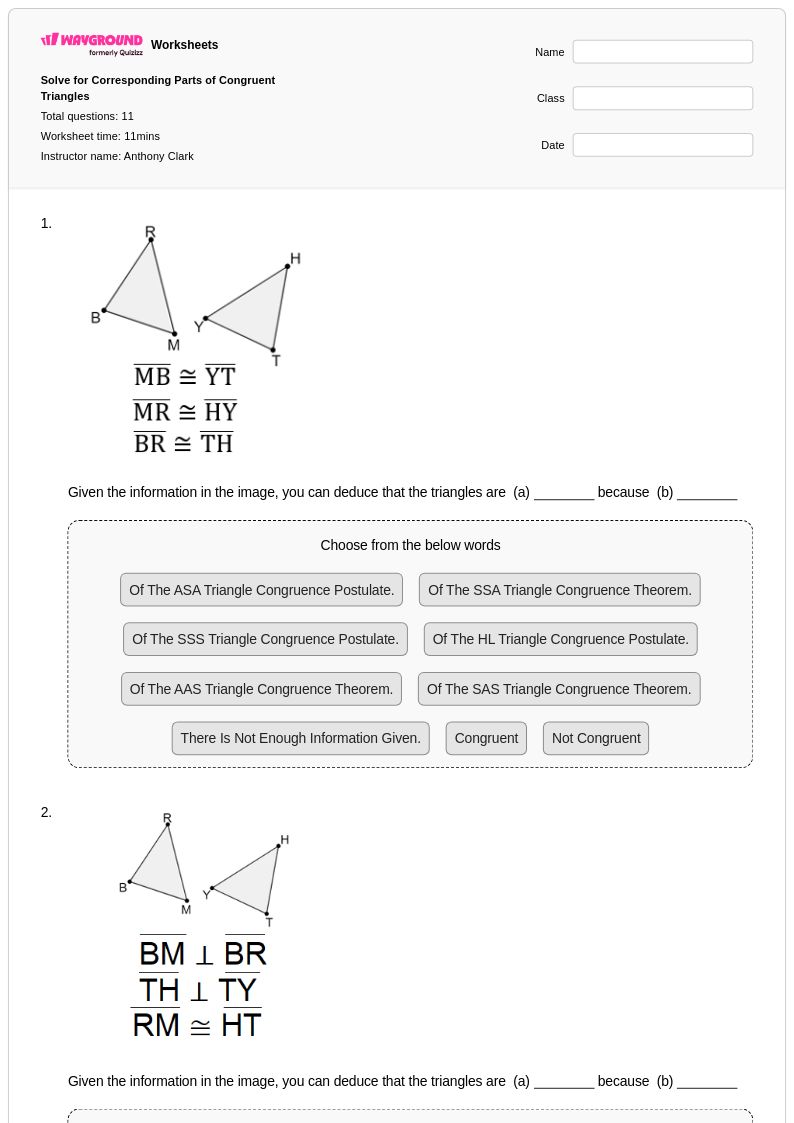
11 คิว
10th - Uni

20 คิว
9th - 12th

12 คิว
9th - 12th
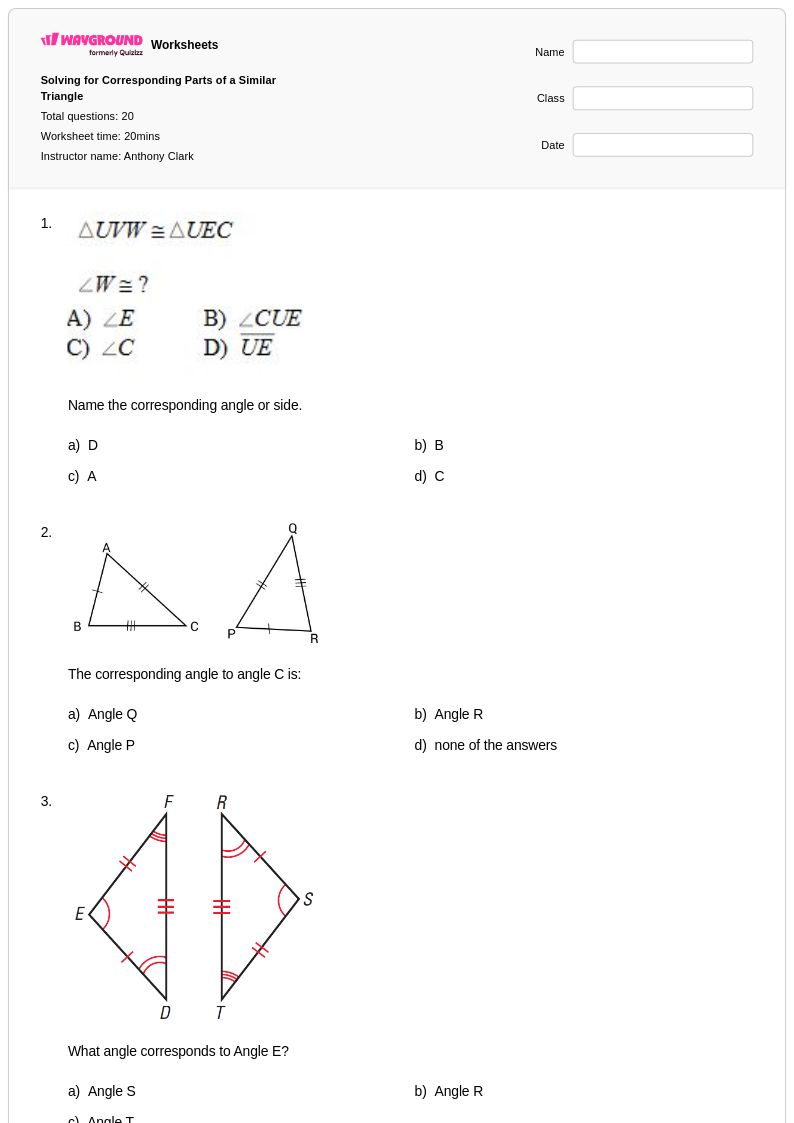
20 คิว
10th - Uni
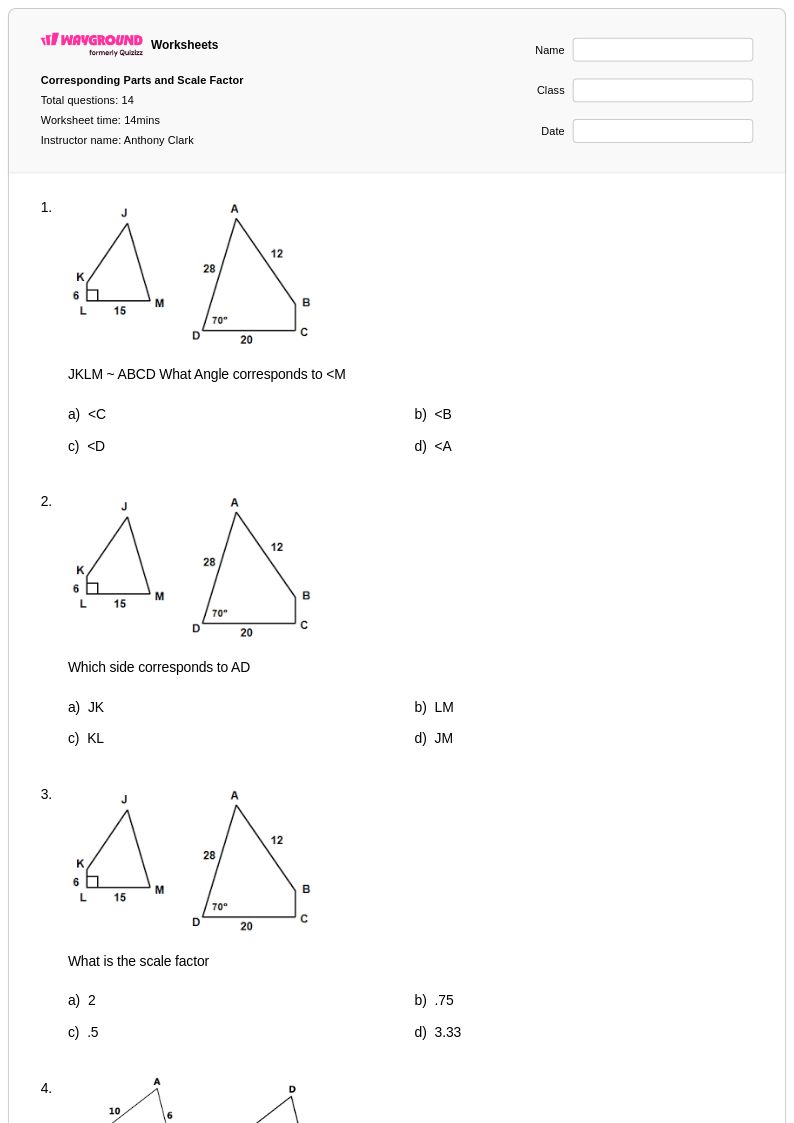
14 คิว
7th - Uni

20 คิว
8th - Uni
15 คิว
10th - Uni

10 คิว
10th - 12th
18 คิว
9th - Uni

15 คิว
6th - 12th

10 คิว
9th - 12th

27 คิว
9th - 12th
5 คิว
9th - 12th
10 คิว
10th - Uni
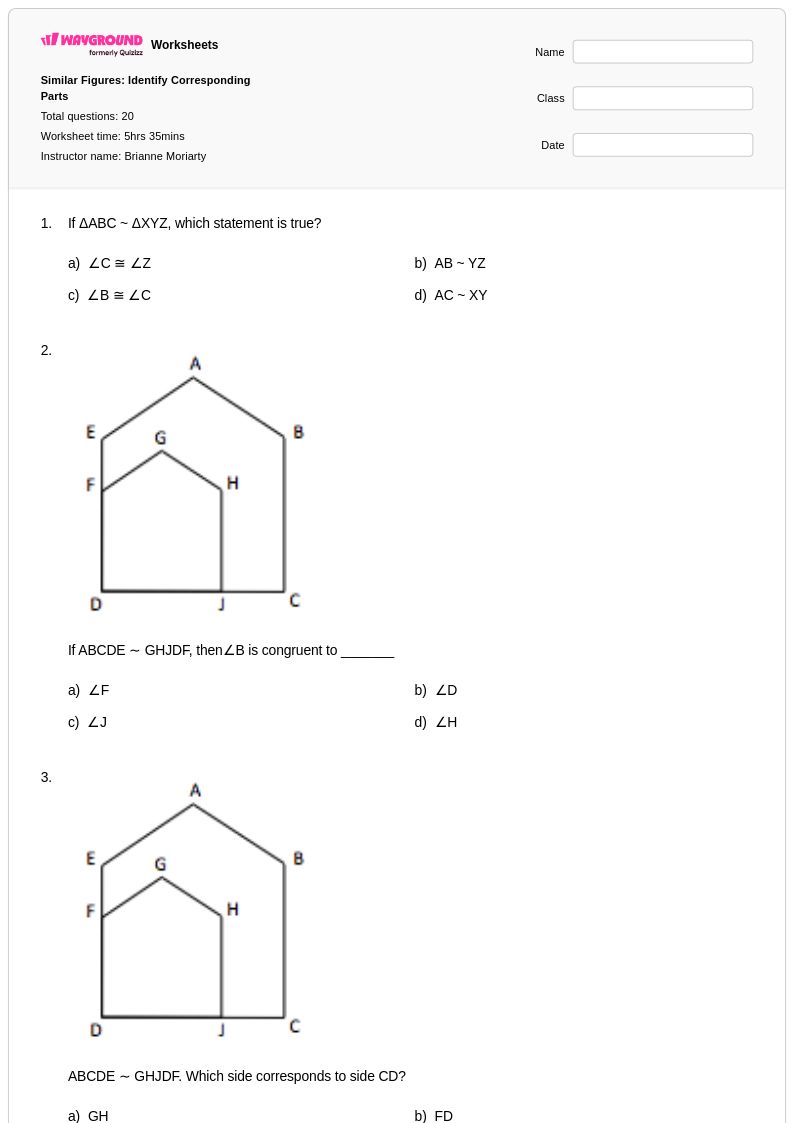
20 คิว
9th - 12th
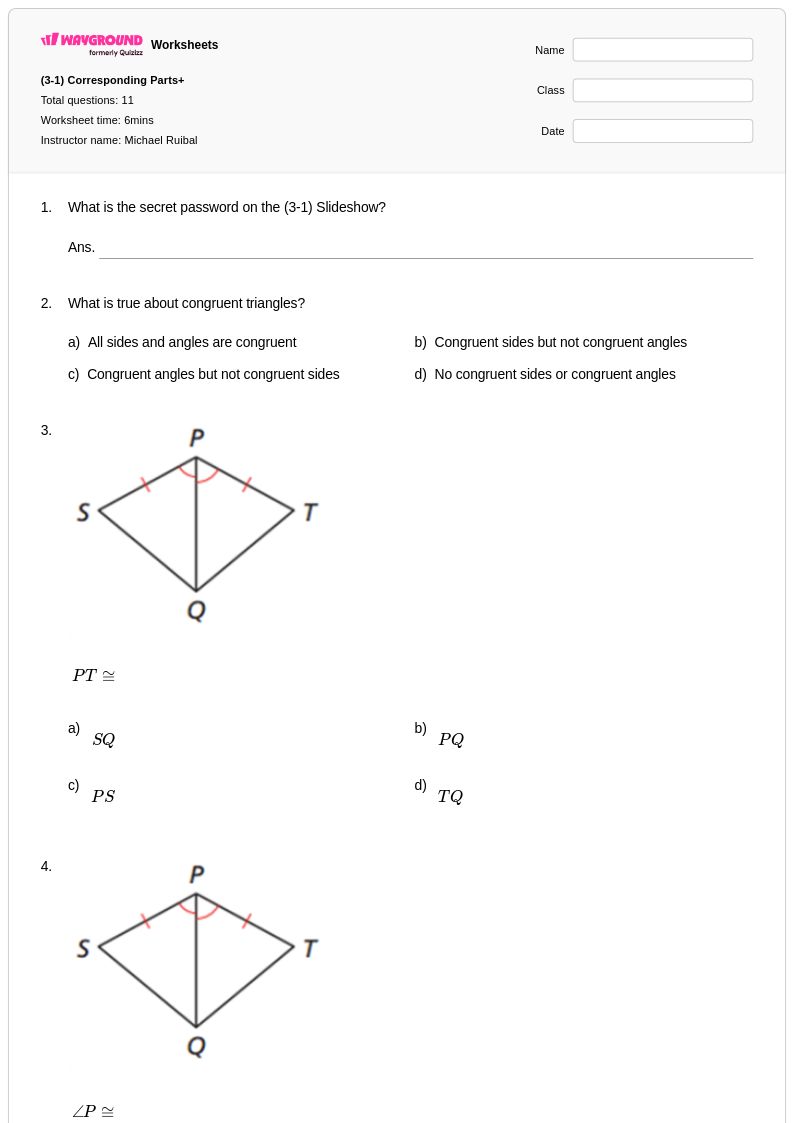
11 คิว
10th - 12th
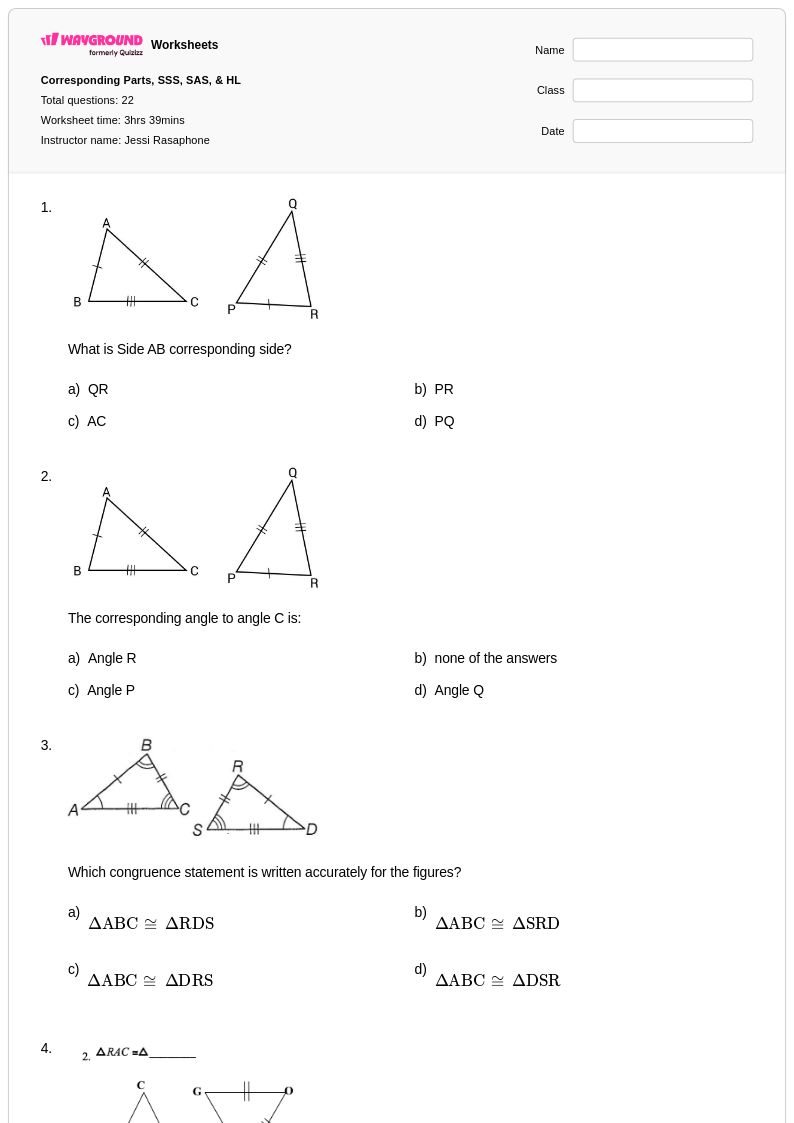
22 คิว
9th - 12th

10 คิว
9th - 12th
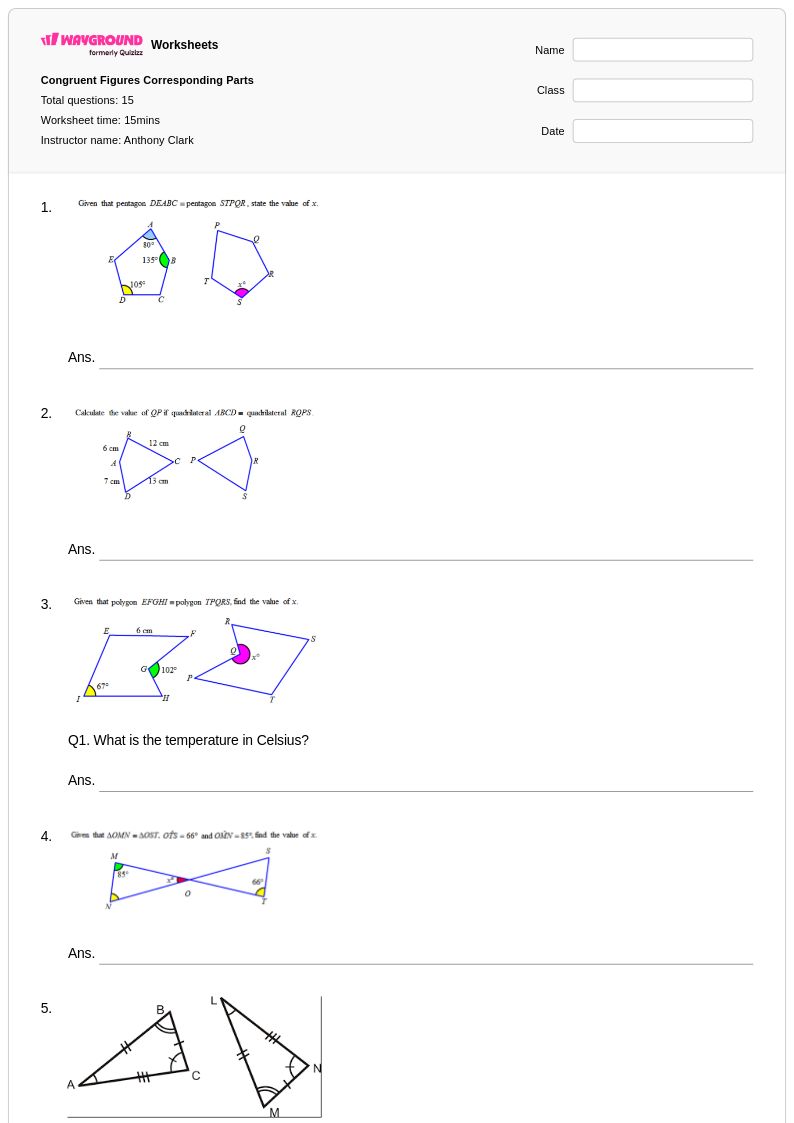
15 คิว
10th - Uni
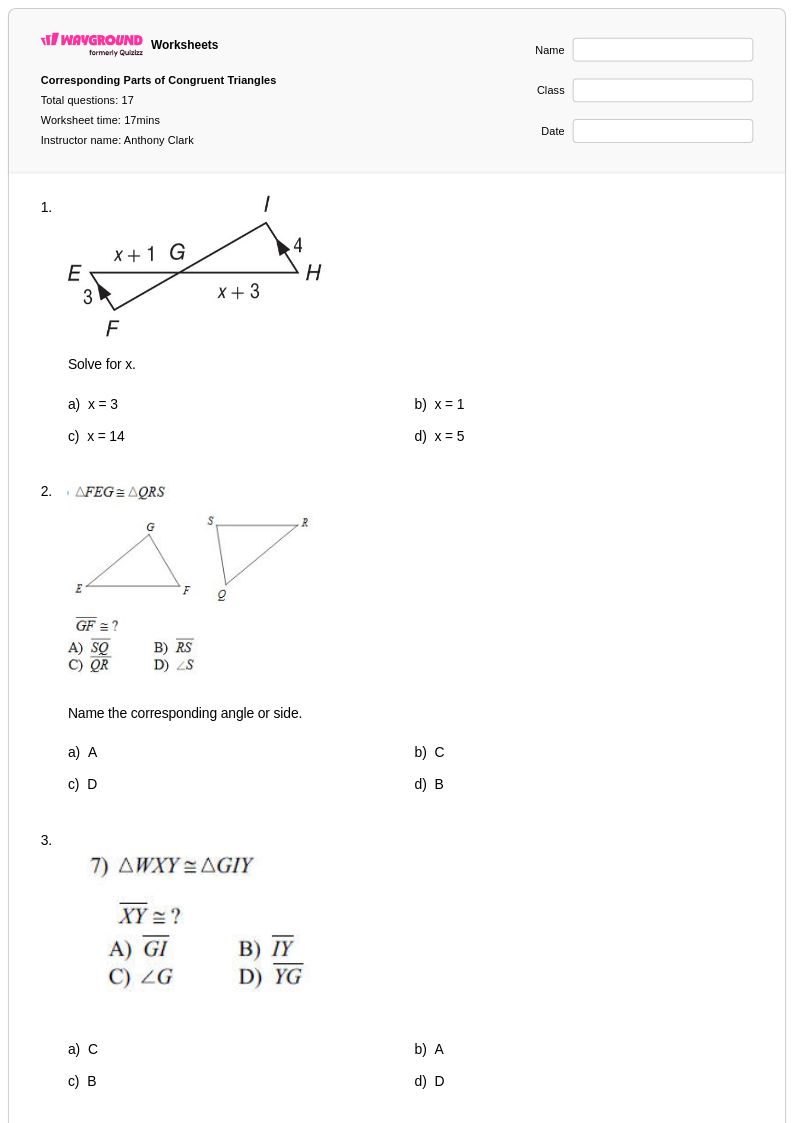
17 คิว
10th - Uni
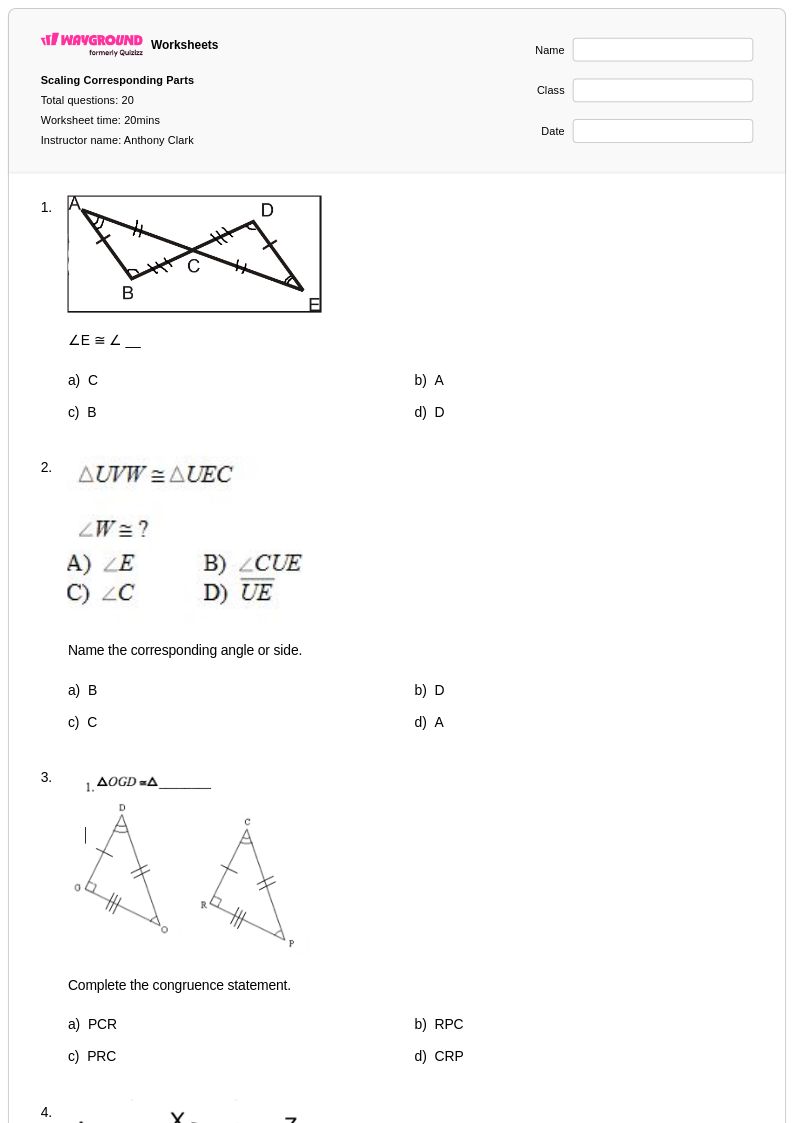
20 คิว
10th - Uni
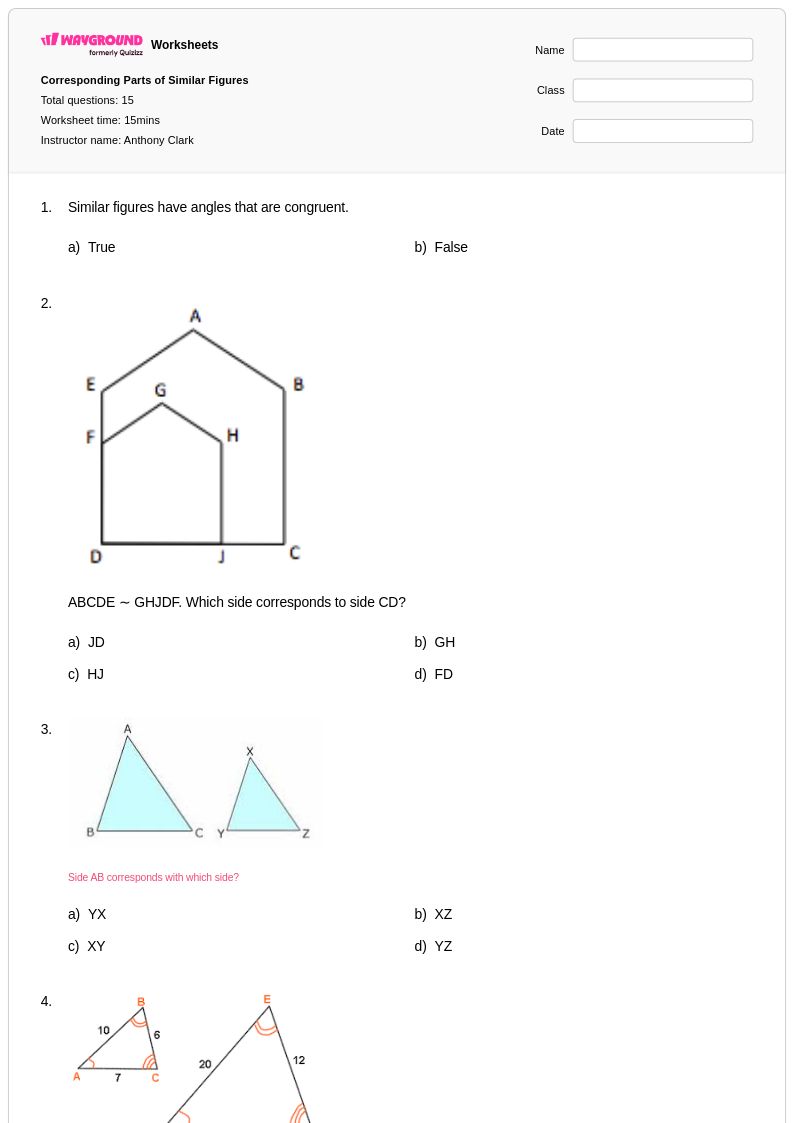
15 คิว
10th - Uni
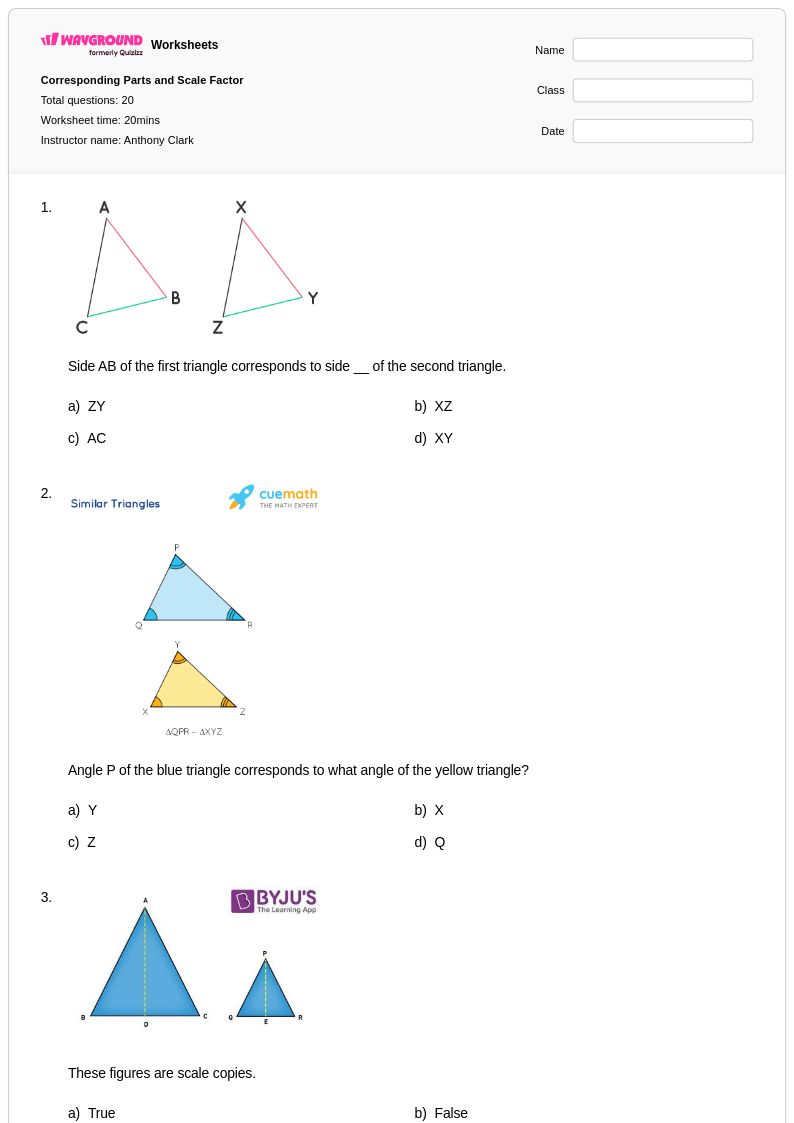
20 คิว
7th - Uni
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 12
สำรวจแผ่นงาน ชิ้นส่วนที่สอดคล้องกัน ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 12
แบบฝึกหัดเรื่องส่วนประกอบที่สอดคล้องกันสำหรับเรขาคณิตระดับชั้น ม.6 ช่วยให้นักเรียนระดับสูงได้ฝึกฝนทักษะการระบุและการทำงานกับส่วนของเส้นตรง มุม และองค์ประกอบทางเรขาคณิตอื่นๆ ที่เท่ากันทุกประการในรูปทรงที่ซับซ้อน แบบฝึกหัดที่ครอบคลุมเหล่านี้ช่วยเสริมสร้างทักษะการวิเคราะห์ที่สำคัญโดยท้าทายให้นักเรียนรู้จักจุดยอด ด้าน และมุมที่สอดคล้องกันในรูปสามเหลี่ยม รูปหลายเหลี่ยม และรูปทรงสามมิติที่เท่ากันทุกประการ พร้อมทั้งประยุกต์ใช้ทฤษฎีบทและสัจพจน์ขั้นสูง แบบฝึกหัดจะค่อยๆ ยากขึ้นเรื่อยๆ ตั้งแต่แบบฝึกหัดการระบุขั้นพื้นฐานไปจนถึงงานเขียนพิสูจน์ที่ซับซ้อน ซึ่งต้องการให้นักเรียนอธิบายเหตุผลโดยใช้ภาษาเรขาคณิตที่เป็นทางการ แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียด และมีให้ดาวน์โหลดเป็นไฟล์ PDF ฟรี ช่วยให้นักเรียนได้ฝึกฝนสถานการณ์ที่ท้าทายมากขึ้นเรื่อยๆ เกี่ยวกับส่วนประกอบที่สอดคล้องกันในการแปลงรูป ความสัมพันธ์แบบคล้ายคลึงกัน และการสร้างรูปทรงเรขาคณิตที่ซับซ้อน
Wayground (เดิมชื่อ Quizizz) สนับสนุนครูคณิตศาสตร์ด้วยคลังแบบฝึกหัดเรื่องส่วนประกอบที่สอดคล้องกันที่สร้างโดยครูหลายล้านชุด ซึ่งออกแบบมาโดยเฉพาะสำหรับการสอนเรขาคณิตระดับชั้น ม.6 แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูสามารถค้นหาแหล่งข้อมูลที่สอดคล้องกับมาตรฐานหลักสูตรเฉพาะและตรงกับระดับทักษะของนักเรียนได้อย่างรวดเร็ว ในขณะที่เครื่องมือการปรับระดับความยากง่ายช่วยให้สามารถปรับระดับความยากและความซับซ้อนของเนื้อหาได้อย่างราบรื่น ครูสามารถเข้าถึงสื่อเหล่านี้ได้ทั้งในรูปแบบไฟล์ PDF ที่พิมพ์ได้และเวอร์ชันดิจิทัลแบบโต้ตอบ ซึ่งให้ความยืดหยุ่นสำหรับการสอนในห้องเรียน การบ้าน และการเรียนรู้ด้วยตนเอง ชุดแบบฝึกหัดที่ครอบคลุมนี้มีประโยชน์ต่อการเรียนการสอนหลายด้าน ตั้งแต่การฝึกฝนทักษะและการเสริมสร้างแนวคิด ไปจนถึงการสนับสนุนการแก้ไขปัญหาสำหรับผู้เรียนที่ประสบปัญหา และโอกาสในการเสริมสร้างความรู้สำหรับนักเรียนที่มีความสามารถสูงที่พร้อมจะรับมือกับความท้าทายด้านการให้เหตุผลทางเรขาคณิตที่ซับซ้อนยิ่งขึ้น
