
20 คิว
5th - Uni

16 คิว
7th - 8th

20 คิว
5th - Uni
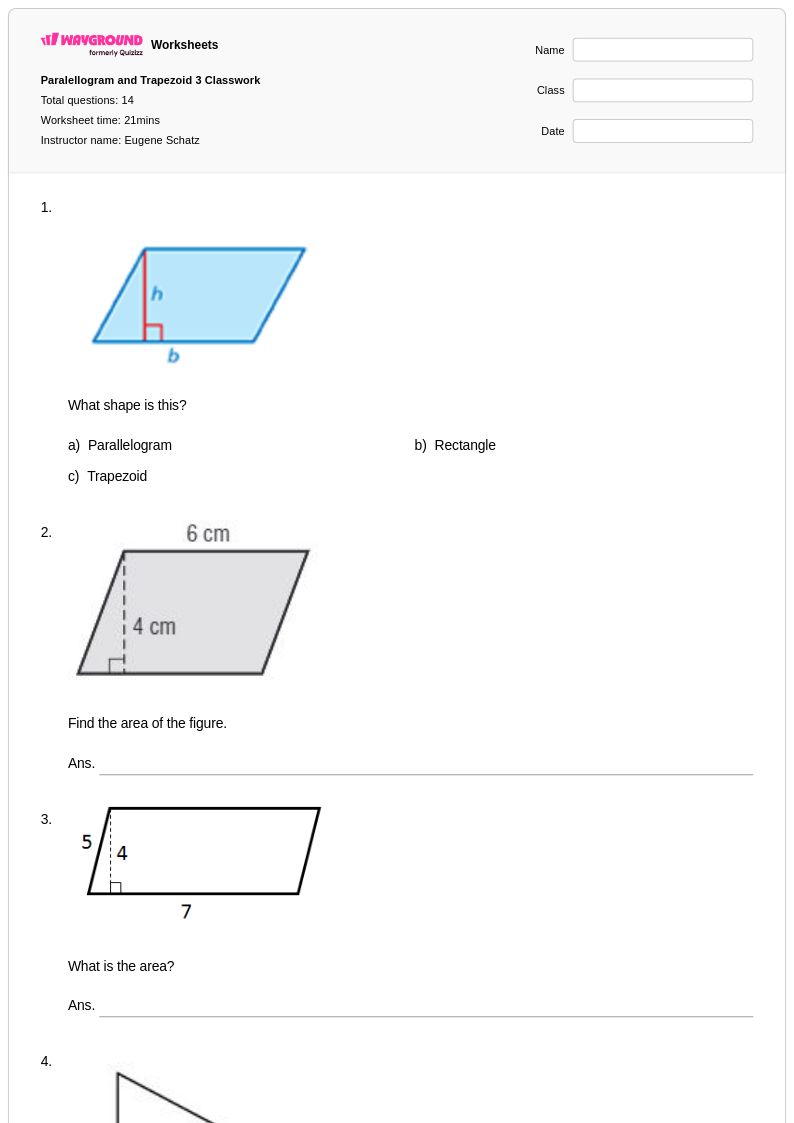
14 คิว
7th
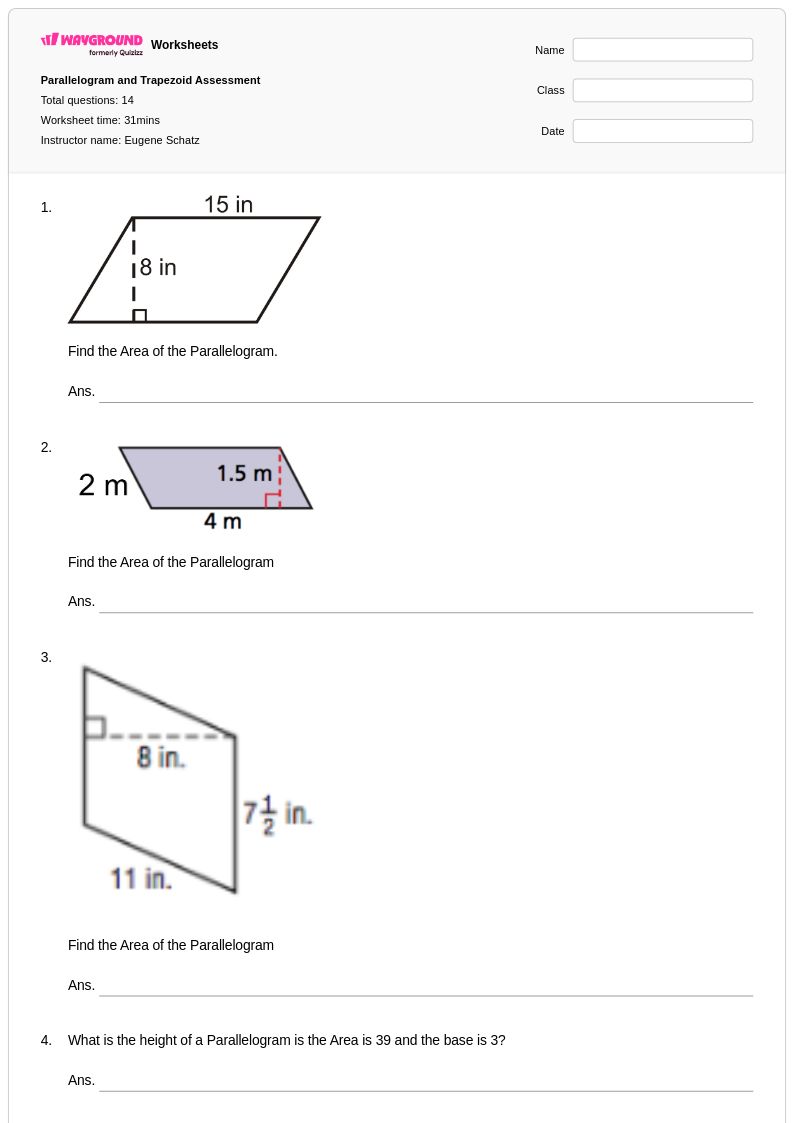
14 คิว
7th
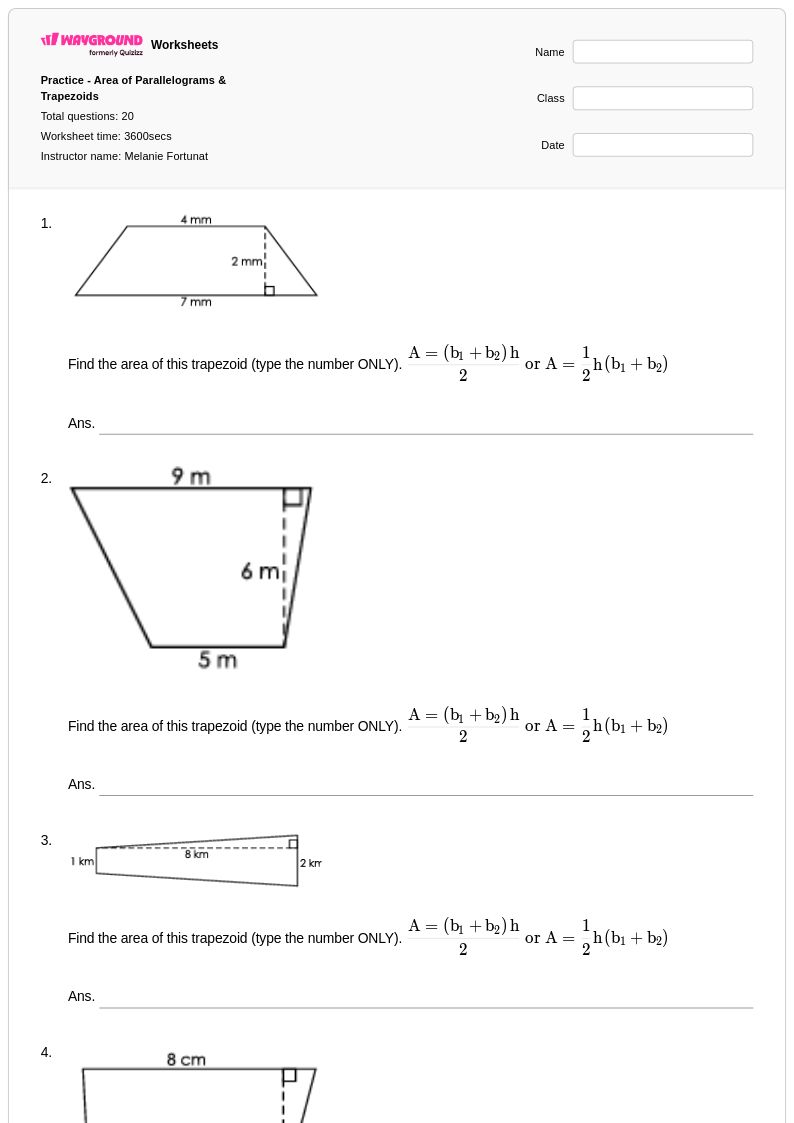
20 คิว
7th

15 คิว
6th - 7th

15 คิว
6th - 7th

17 คิว
6th - Uni
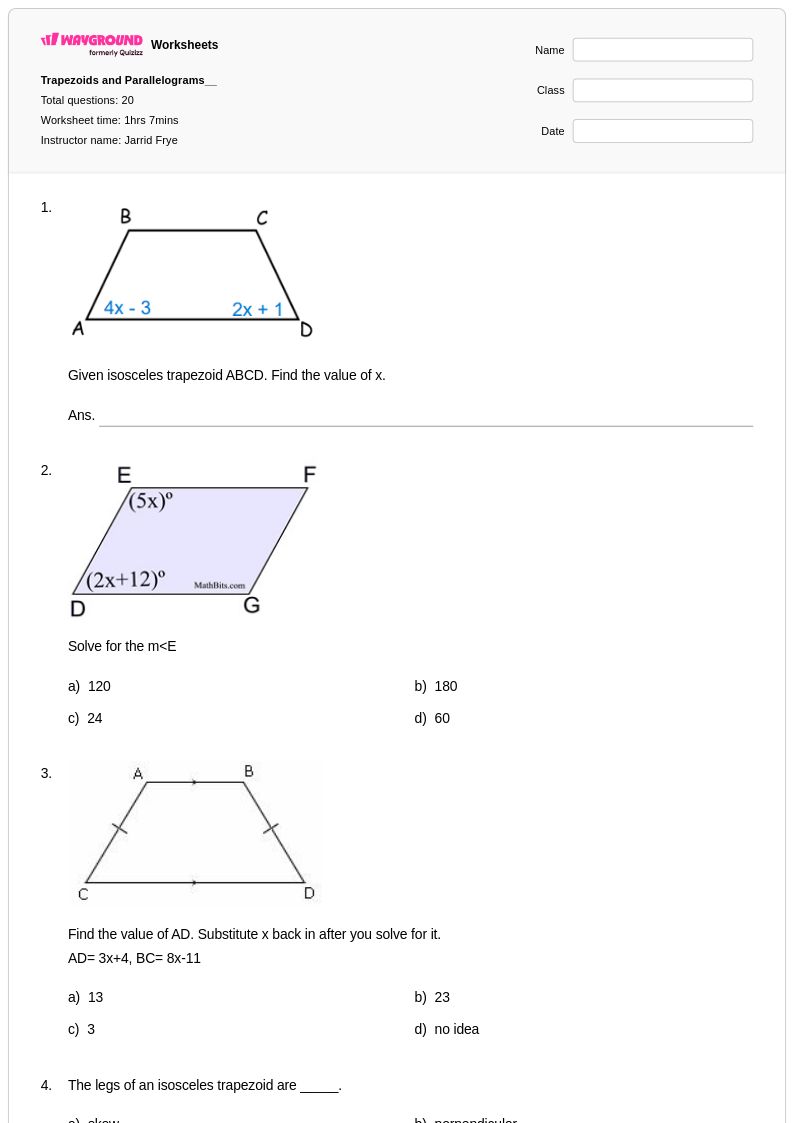
20 คิว
6th - 8th

15 คิว
6th - Uni
20 คิว
7th - Uni

20 คิว
7th - 9th
22 คิว
6th - 8th

8 คิว
6th - Uni

20 คิว
3rd - Uni
20 คิว
5th - Uni
42 คิว
7th
20 คิว
6th - 8th
20 คิว
5th - Uni

18 คิว
7th
19 คิว
3rd - Uni

21 คิว
6th - 8th
20 คิว
5th - Uni
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 7
สำรวจแผ่นงาน ทฤษฎีบทส่วนกลางรูปสี่เหลี่ยมคางหมู ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 7
แบบฝึกหัดทฤษฎีบทส่วนกลางของรูปสี่เหลี่ยมคางหมูสำหรับนักเรียนชั้น ม.1 จาก Wayground เป็นแบบฝึกหัดที่ครอบคลุมเกี่ยวกับหนึ่งในแนวคิดพื้นฐานที่สำคัญที่สุดของเรขาคณิต แหล่งข้อมูลที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยให้นักเรียนเข้าใจหลักการที่ว่า ส่วนกลางของรูปสี่เหลี่ยมคางหมูนั้นขนานกับฐานทั้งสองและมีความยาวเท่ากับค่าเฉลี่ยของความยาวฐานทั้งสอง แบบฝึกหัดเหล่านี้เสริมสร้างทักษะทางคณิตศาสตร์ที่สำคัญ ได้แก่ การให้เหตุผลทางเรขาคณิต การประยุกต์ใช้เรขาคณิตพิกัด การแก้ปัญหาพีชคณิต และการสร้างบทพิสูจน์ ผ่านแบบฝึกหัดที่หลากหลาย ตั้งแต่แบบฝึกหัดการระบุพื้นฐานไปจนถึงการคำนวณหลายขั้นตอนที่ซับซ้อน แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียดและมีให้ดาวน์โหลดเป็นไฟล์ PDF ที่สะดวกต่อการพิมพ์ฟรี ทำให้มั่นใจได้ว่านักเรียนสามารถฝึกฝนแก้ปัญหาได้อย่างเป็นระบบ ในขณะที่ครูสามารถประเมินความเข้าใจและให้ข้อเสนอแนะที่ตรงเป้าหมายได้อย่างมีประสิทธิภาพ
คอลเลกชันแหล่งข้อมูลเกี่ยวกับทฤษฎีบทส่วนกลางของรูปสี่เหลี่ยมคางหมูของ Wayground มาจากสื่อที่สร้างโดยครูหลายล้านคน ทำให้ครูผู้สอนมีฟังก์ชันการค้นหาและการกรองที่มีประสิทธิภาพ เพื่อค้นหาแบบฝึกหัดที่ตรงกับความต้องการในการสอนและข้อกำหนดด้านมาตรฐานได้อย่างแม่นยำ เครื่องมือการปรับระดับความยากง่ายของแพลตฟอร์มนี้ช่วยให้ครูสามารถปรับแต่งระดับความยากง่ายของเนื้อหาได้ ทำให้แหล่งข้อมูลเหล่านี้มีคุณค่าอย่างยิ่งสำหรับการแก้ไขปัญหาการเรียนรู้ของนักเรียนที่อ่อนล้า และการเสริมสร้างความรู้สำหรับนักเรียนที่มีความสามารถสูงที่ต้องการความท้าทายทางเรขาคณิตเพิ่มเติม ชุดแบบฝึกหัดเหล่านี้มีให้เลือกทั้งในรูปแบบไฟล์ PDF ที่สามารถพิมพ์ได้ และเวอร์ชันดิจิทัลแบบโต้ตอบ ช่วยสนับสนุนการวางแผนบทเรียนที่ยืดหยุ่น ในขณะเดียวกันก็มอบโอกาสในการฝึกฝนอย่างต่อเนื่องที่นักเรียนต้องการเพื่อพัฒนาความคล่องแคล่วในการคำนวณส่วนกลาง การประยุกต์ใช้ระนาบพิกัด และเทคนิคการพิสูจน์ทางเรขาคณิต ครูสามารถบูรณาการแหล่งข้อมูลเหล่านี้เข้ากับหลักสูตรได้อย่างราบรื่นเพื่อเสริมการเรียนการสอนในห้องเรียนและเพื่อให้แน่ใจว่านักเรียนสร้างทักษะการให้เหตุผลเชิงพื้นที่ที่จำเป็นต่อความสำเร็จในแนวคิดเรขาคณิตขั้นสูง
