หัวข้อแนะนำสำหรับคุณ

20 คิว
6th - 8th

13 คิว
6th - 8th

10 คิว
7th - 9th

10 คิว
1st - 10th

8 คิว
6th - 8th

11 คิว
6th - 8th

30 คิว
6th - 8th

20 คิว
1st - 12th
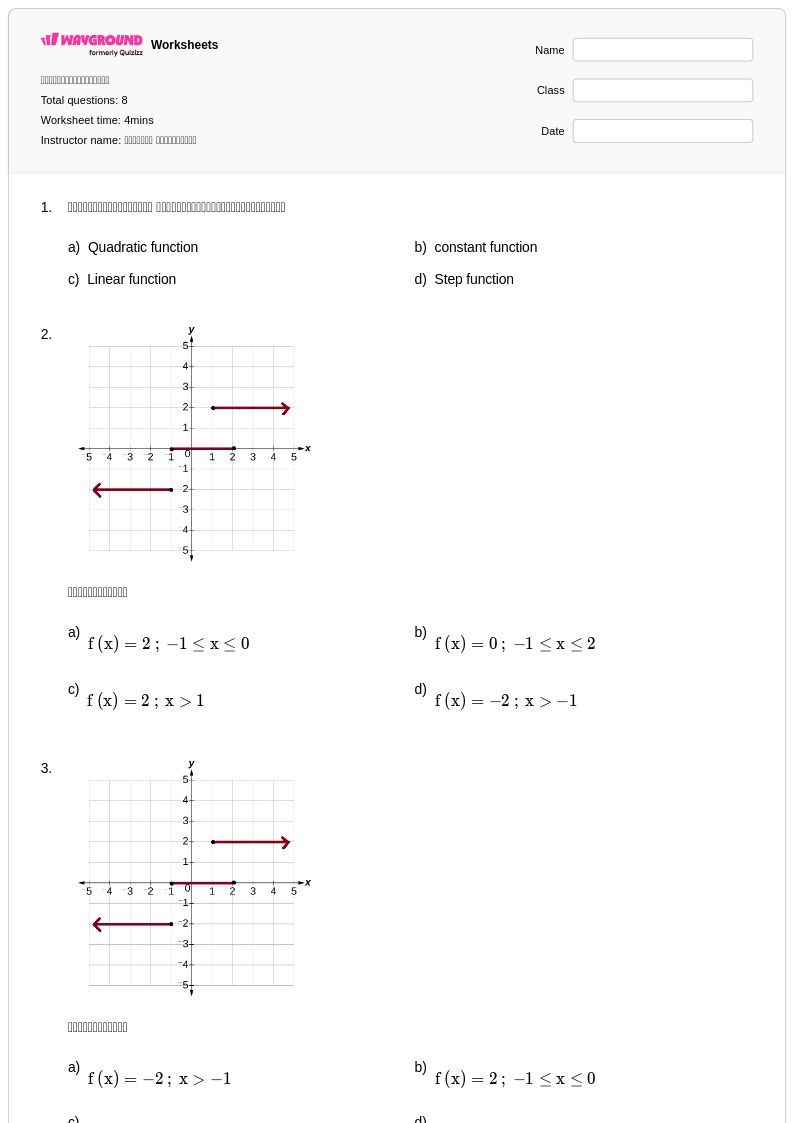
8 คิว
6th - 8th

20 คิว
6th - 8th

30 คิว
7th - 9th
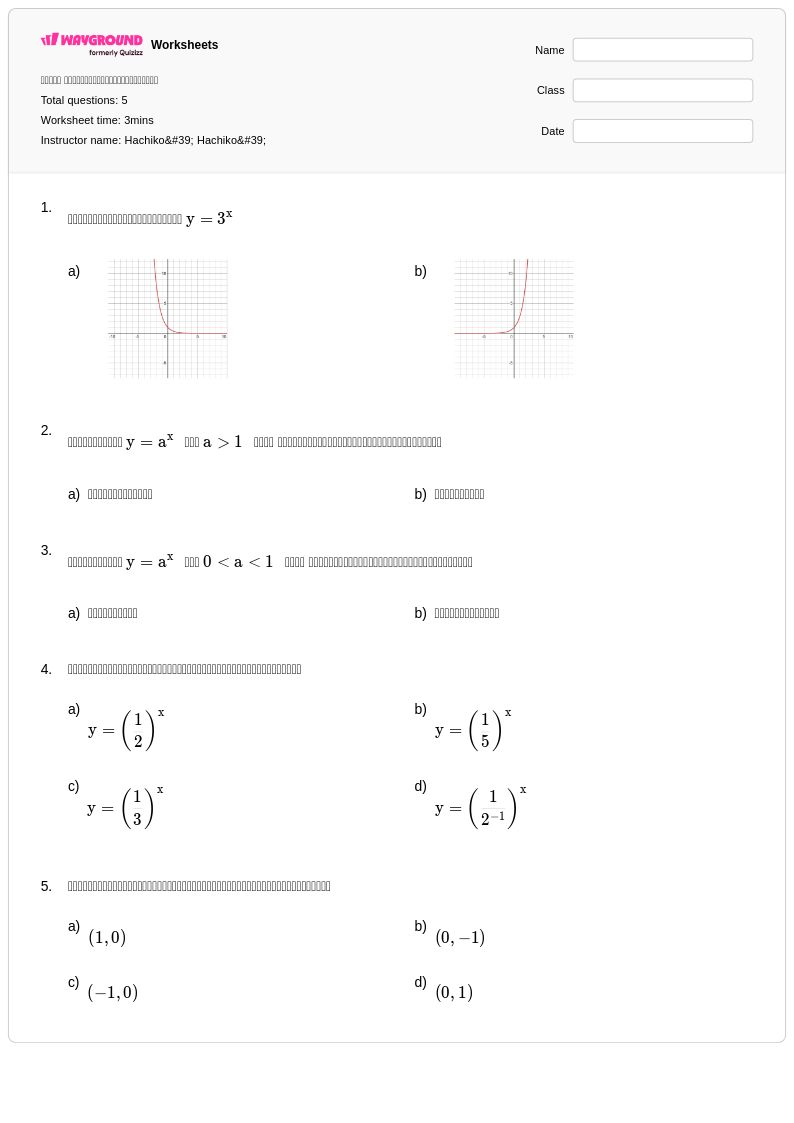
5 คิว
KG - 11th

45 คิว
1st - 12th

30 คิว
6th - 8th
สำรวจแผ่นงาน ฟังก์ชั่น สำหรับ ระดับ 7 ตามหัวข้อ
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 7
สำรวจแผ่นงาน ฟังก์ชั่น ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 7
แบบฝึกหัดเรื่องฟังก์ชันสำหรับนักเรียนชั้น ม.1 (เกรด 7) จาก Wayground (เดิมคือ Quizizz) มอบโอกาสในการฝึกฝนอย่างครอบคลุมสำหรับนักเรียนที่เริ่มต้นศึกษาความสัมพันธ์เชิงฟังก์ชันในวิชาพีชคณิตอย่างเป็นทางการ แบบฝึกหัดที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยเสริมสร้างทักษะที่สำคัญ ได้แก่ การระบุฟังก์ชันจากตาราง กราฟ และสมการ การหาโดเมนและเรนจ์ การประเมินสัญลักษณ์ฟังก์ชัน และการแยกแยะรูปแบบเชิงเส้นและไม่เชิงเส้น นักเรียนจะได้ทำแบบฝึกหัดที่สร้างความเข้าใจเชิงแนวคิดว่าค่าอินพุตสอดคล้องกับค่าเอาต์พุตที่ไม่ซ้ำกันอย่างไร พร้อมทั้งพัฒนาความคล่องแคล่วในการใช้คำศัพท์และสัญลักษณ์ฟังก์ชัน แบบฝึกหัดแต่ละชุดมีเฉลยคำตอบครบถ้วนและมีให้ดาวน์โหลดเป็นไฟล์ PDF ที่พิมพ์ได้ฟรี ทำให้ครูผู้สอนสามารถประเมินความก้าวหน้าของนักเรียนและให้ข้อเสนอแนะที่ตรงเป้าหมายเกี่ยวกับแนวคิดพื้นฐานทางพีชคณิตนี้ได้อย่างง่ายดาย
Wayground (เดิมคือ Quizizz) สนับสนุนครูผู้สอนวิชาคณิตศาสตร์ด้วยแหล่งข้อมูลที่สร้างโดยครูผู้สอนนับล้านรายการ ซึ่งเน้นเฉพาะการสอนเรื่องฟังก์ชันสำหรับนักเรียนชั้น ม.1 ความสามารถในการค้นหาและกรองข้อมูลที่แข็งแกร่งของแพลตฟอร์มช่วยให้ครูผู้สอนสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานการเรียนรู้เฉพาะและปรับระดับความยากง่ายได้ตามระดับทักษะต่างๆ ในห้องเรียนได้อย่างรวดเร็ว ครูสามารถปรับแต่งแบบฝึกหัดที่มีอยู่แล้วหรือสร้างแบบฝึกหัดใหม่ได้โดยใช้เครื่องมือดิจิทัลที่ยืดหยุ่น จากนั้นจึงแจกจ่ายสื่อการเรียนการสอนได้อย่างราบรื่นทั้งในรูปแบบไฟล์ PDF ที่พิมพ์ได้และเวอร์ชันดิจิทัลแบบโต้ตอบ เพื่อรองรับความต้องการในการเรียนรู้ที่หลากหลาย คลังทรัพยากรที่ครอบคลุมนี้ช่วยให้การวางแผนบทเรียนมีประสิทธิภาพ ในขณะเดียวกันก็มอบแบบฝึกหัดที่ตรงเป้าหมายสำหรับการแก้ไขจุดอ่อน การเสริมสร้างทักษะ และกิจกรรมเสริมที่ช่วยให้นักเรียนเชี่ยวชาญในการเปลี่ยนผ่านที่สำคัญจากการคิดเชิงพีชคณิตขั้นพื้นฐานไปสู่ความเข้าใจความสัมพันธ์เชิงฟังก์ชัน
