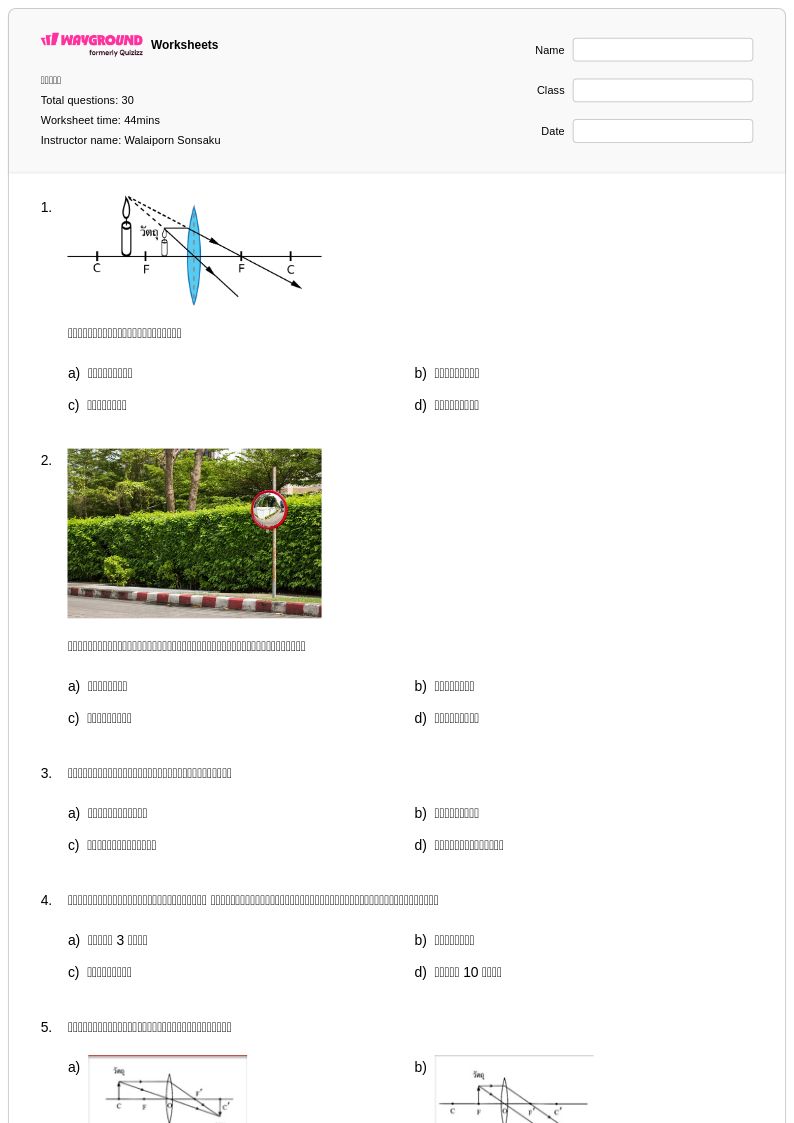
30 คิว
8th

31 คิว
6th - 8th

16 คิว
7th

15 คิว
6th

10 คิว
8th

10 คิว
12th

20 คิว
9th
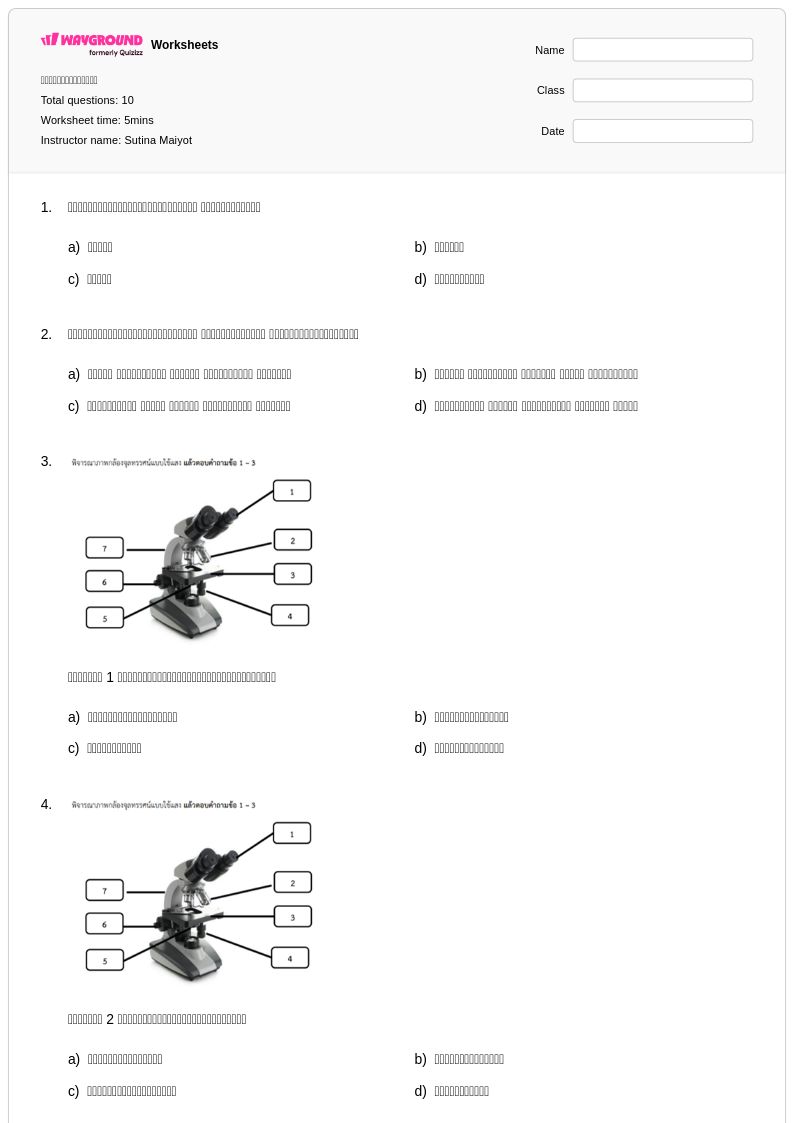
10 คิว
7th

10 คิว
8th
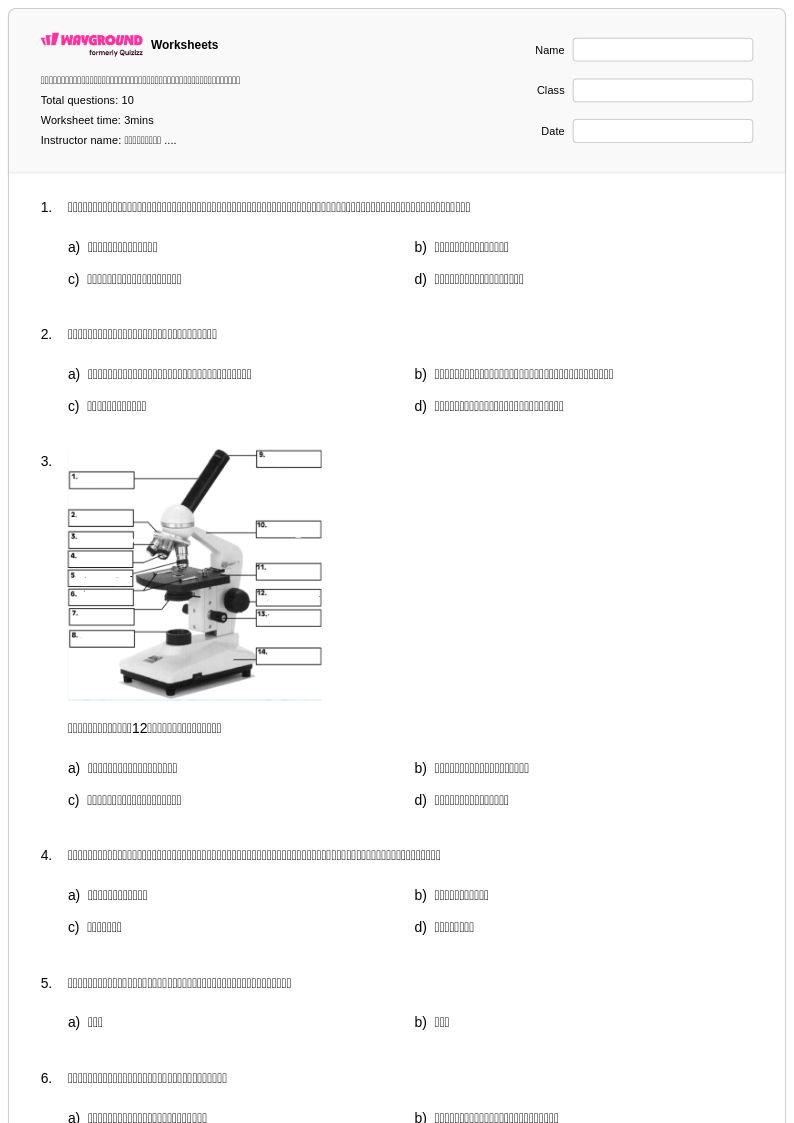
10 คิว
9th

25 คิว
9th

20 คิว
9th - 12th
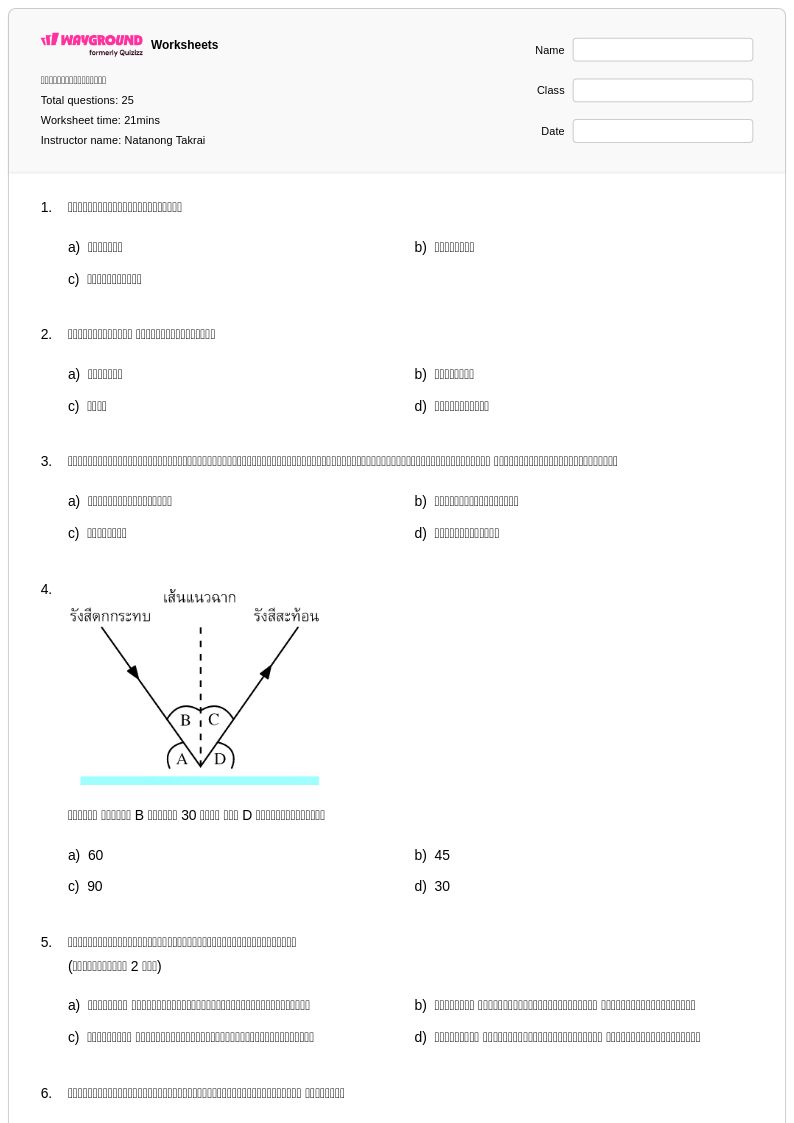
25 คิว
9th - 12th

10 คิว
7th

7 คิว
9th - 12th

41 คิว
1st
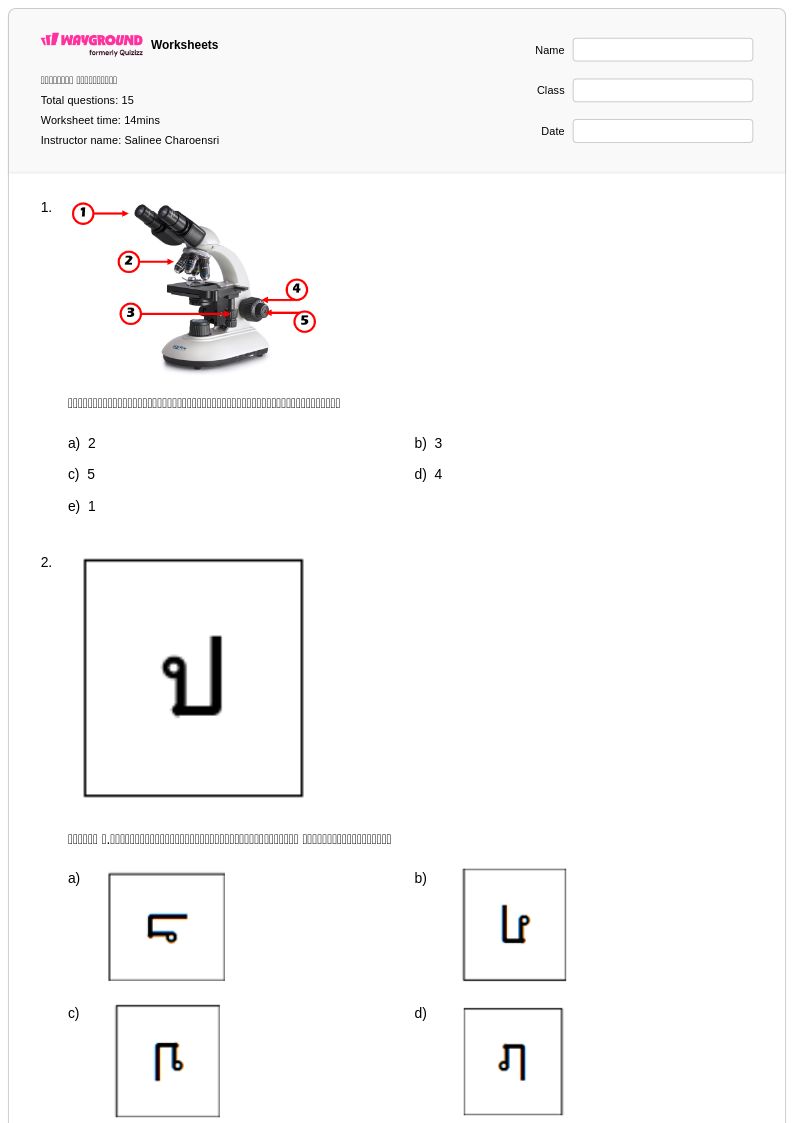
15 คิว
7th
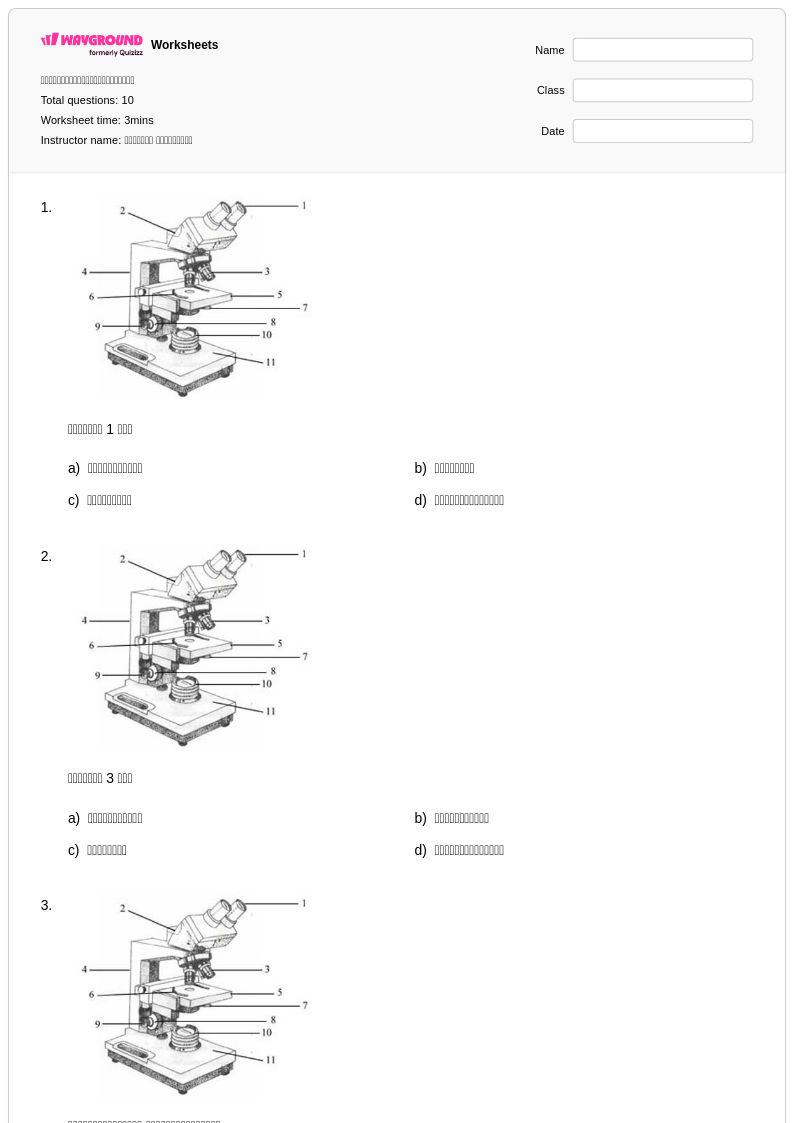
10 คิว
7th
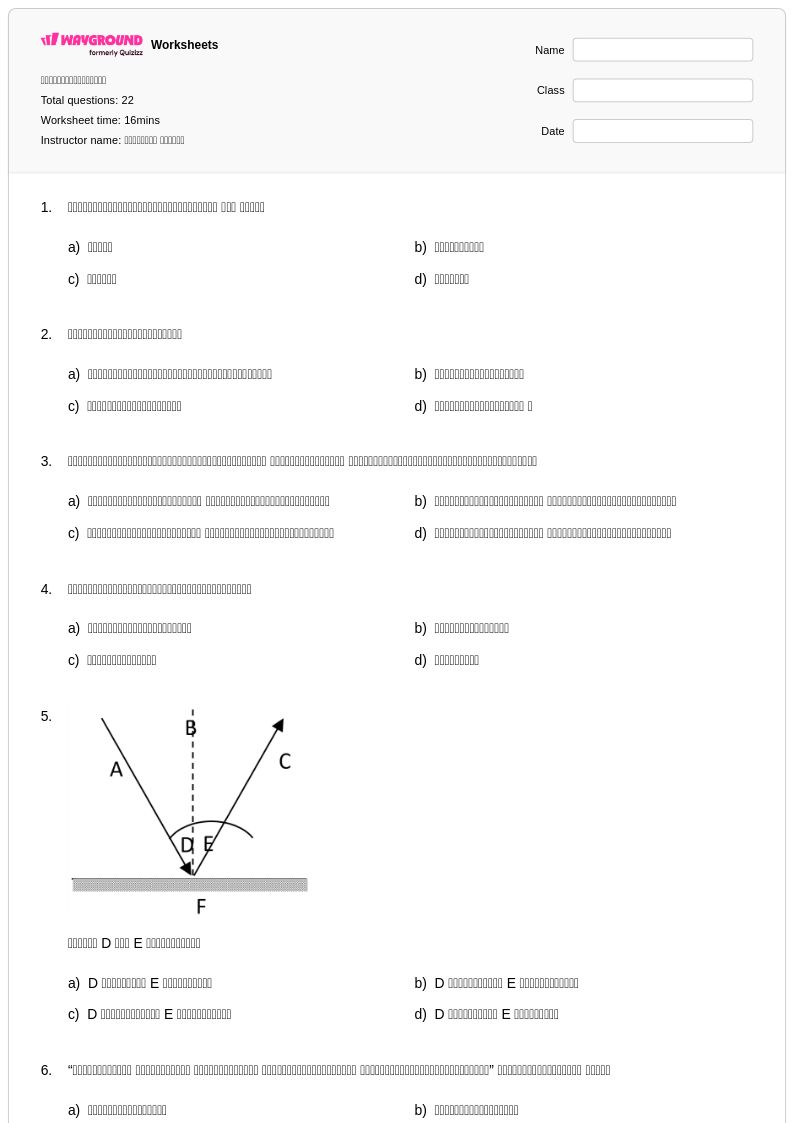
22 คิว
8th

35 คิว
7th

15 คิว
7th

25 คิว
3rd

20 คิว
9th

20 คิว
4th
สำรวจแผ่นงานตามหัวเรื่อง
สำรวจแผ่นงาน เลนส์ ที่พิมพ์ได้
แบบฝึกหัดเรื่องเลนส์จาก Wayground (เดิมคือ Quizizz) มีแบบฝึกหัดที่ครอบคลุมสำหรับนักเรียนที่ต้องการศึกษาหลักการพื้นฐานของทัศนศาสตร์เชิงเรขาคณิต แหล่งข้อมูลทางการศึกษาเหล่านี้เน้นที่แนวคิดสำคัญเกี่ยวกับเลนส์ ได้แก่ เลนส์รวมแสงและเลนส์กระจายแสง การคำนวณความยาวโฟกัส แผนภาพรังสี การสร้างภาพ และหลักการขยาย แบบฝึกหัดเหล่านี้ช่วยเสริมสร้างทักษะการวิเคราะห์เชิงวิพากษ์ผ่านแบบฝึกหัดที่เป็นระบบ ซึ่งจะนำนักเรียนไปสู่การประยุกต์ใช้สมการเลนส์ ความสัมพันธ์ระหว่างระยะห่างของวัตถุและภาพ และความแตกต่างระหว่างภาพจริงและภาพเสมือน แหล่งข้อมูลแต่ละชุดมีเฉลยคำตอบโดยละเอียดเพื่อสนับสนุนการเรียนรู้ด้วยตนเองและการประเมินตนเอง ในขณะที่รูปแบบไฟล์ PDF ที่พิมพ์ได้ฟรีช่วยให้เข้าถึงได้ทั้งสำหรับการเรียนการสอนในห้องเรียนและการศึกษาที่บ้าน สื่อการฝึกฝนเหล่านี้เชื่อมโยงความเข้าใจเชิงทฤษฎีกับความสามารถในการแก้ปัญหาเชิงปฏิบัติได้อย่างมีประสิทธิภาพ ซึ่งจำเป็นต่อการเรียนรู้หลักการของทัศนศาสตร์เชิงเรขาคณิต
Wayground (เดิมคือ Quizizz) สนับสนุนนักการศึกษาด้วยชุดแบบฝึกหัดเรื่องเลนส์ที่สร้างโดยครูหลายล้านชุด ซึ่งช่วยให้การวางแผนบทเรียนและการสอนที่แตกต่างกันเป็นไปอย่างราบรื่น แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูสามารถค้นหาแหล่งข้อมูลที่สอดคล้องกับมาตรฐานการเรียนรู้และระดับทักษะเฉพาะได้อย่างรวดเร็ว ตั้งแต่แนวคิดเบื้องต้นเกี่ยวกับเลนส์ไปจนถึงการคำนวณทางแสงขั้นสูง เครื่องมือปรับแต่งช่วยให้ครูสามารถแก้ไขแบบฝึกหัดที่มีอยู่หรือสร้างแบบฝึกหัดที่ปรับให้เหมาะสมกับความต้องการของนักเรียนแต่ละคน สนับสนุนทั้งการแก้ไขปัญหาสำหรับนักเรียนที่เรียนรู้ช้าและโอกาสในการเสริมสร้างความรู้สำหรับนักเรียนที่เรียนรู้สูง แหล่งข้อมูลอเนกประสงค์เหล่านี้มีให้เลือกทั้งในรูปแบบไฟล์ PDF ที่สามารถพิมพ์ได้และแบบดิจิทัล ช่วยให้สามารถบูรณาการเข้ากับสภาพแวดล้อมการสอนต่างๆ ได้อย่างราบรื่น พร้อมทั้งมอบโอกาสในการฝึกฝนทักษะและการประเมินผลอย่างต่อเนื่องในการศึกษาด้านทัศนศาสตร์เชิงเรขาคณิต
