
20 คิว
5th - Uni

20 คิว
8th

20 คิว
5th - Uni

11 คิว
8th

9 คิว
8th - Uni
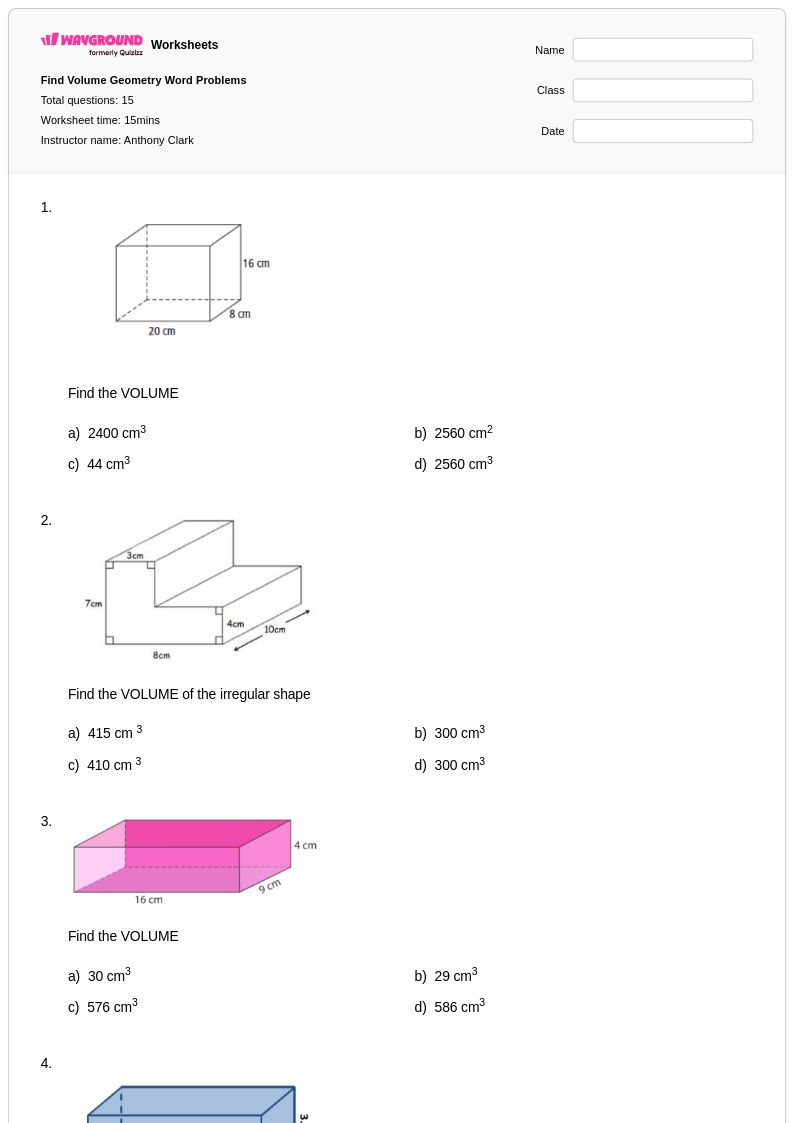
15 คิว
5th - Uni

15 คิว
5th - Uni
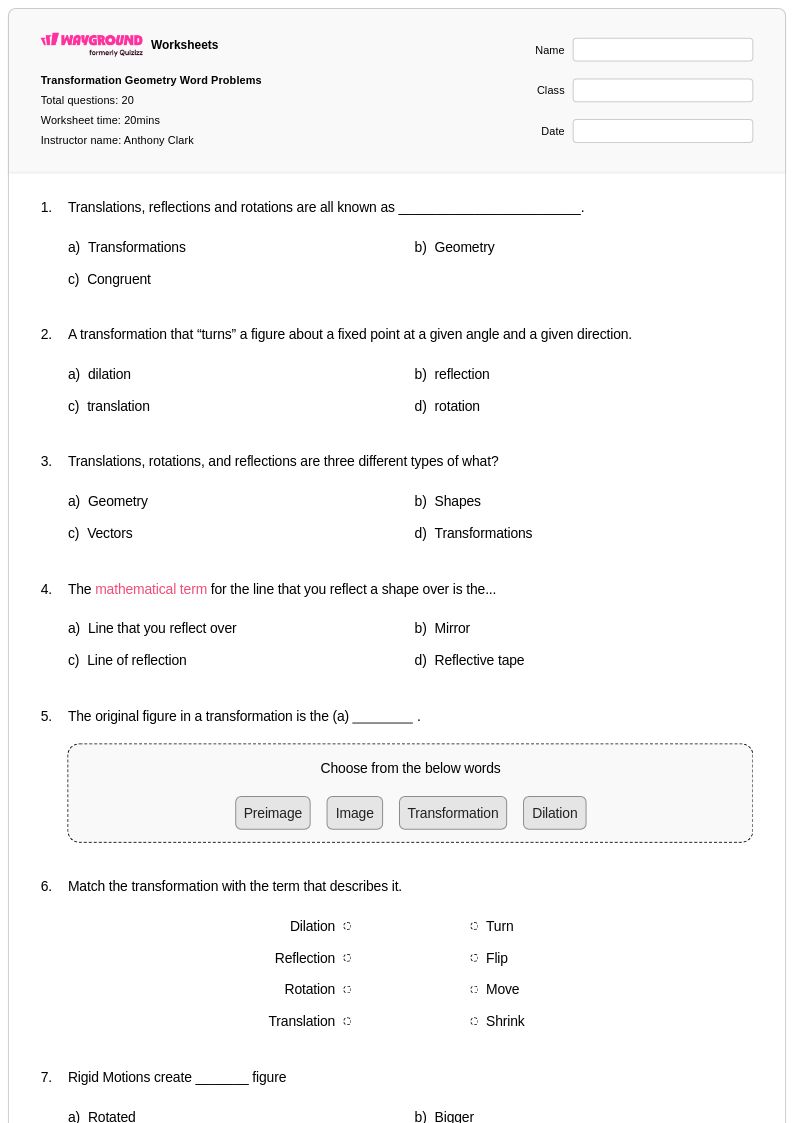
20 คิว
8th - Uni

15 คิว
8th

9 คิว
8th - Uni

28 คิว
8th

20 คิว
8th - Uni

12 คิว
8th

17 คิว
1st - PD
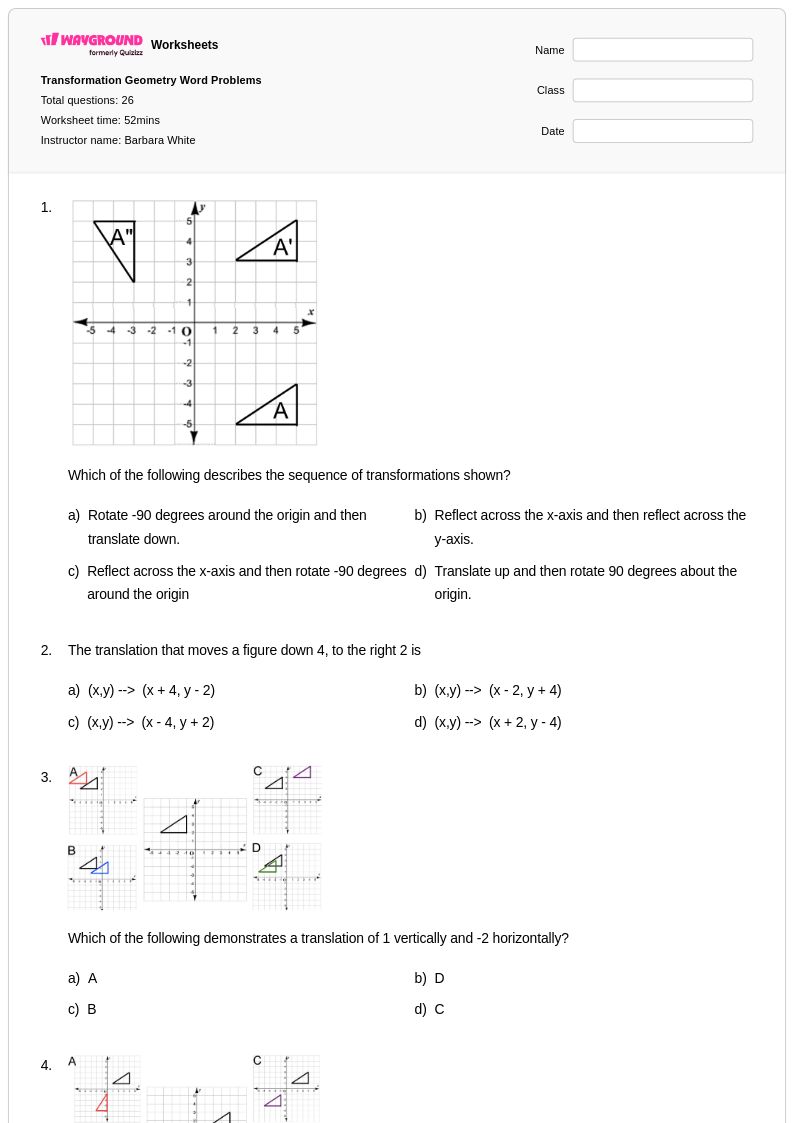
26 คิว
8th - 10th

17 คิว
8th
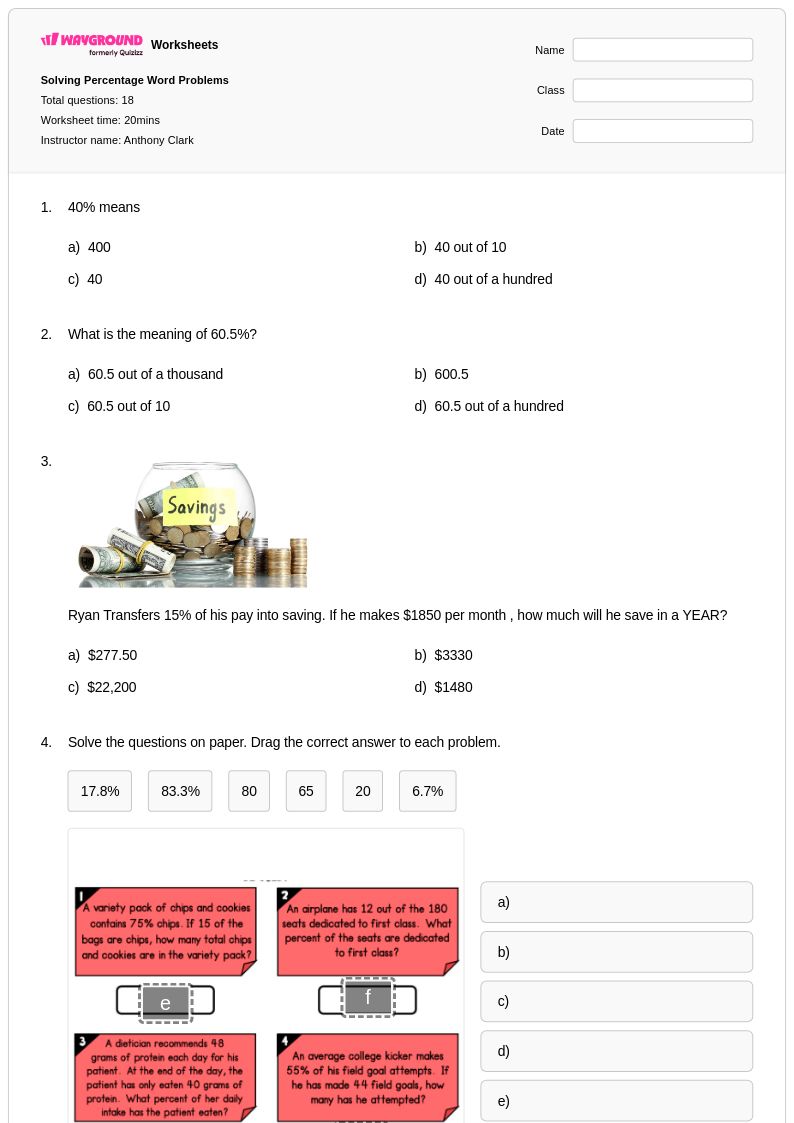
20 คิว
7th - Uni

10 คิว
7th - 10th

10 คิว
8th
20 คิว
5th - Uni

20 คิว
7th - Uni
10 คิว
5th - Uni

20 คิว
8th
10 คิว
7th - 8th
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 8
สำรวจแผ่นงาน โจทย์ปัญหาเรขาคณิต ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 8
แบบฝึกหัดเรขาคณิตระดับชั้น ม.2 (เกรด 8) จาก Wayground (เดิมคือ Quizizz) ช่วยให้นักเรียนได้ฝึกฝนการประยุกต์ใช้แนวคิดทางเรขาคณิตกับสถานการณ์ในชีวิตจริงและสถานการณ์ทางคณิตศาสตร์อย่างครอบคลุม แบบฝึกหัดเหล่านี้ช่วยเสริมสร้างทักษะการคิดเชิงวิเคราะห์ โดยให้นักเรียนตีความโจทย์ปัญหาที่ซับซ้อน ระบุความสัมพันธ์ทางเรขาคณิตที่เกี่ยวข้อง และประยุกต์ใช้สูตรสำหรับพื้นที่ ปริมาตร เส้นรอบวง และการวัดมุมในบริบทเชิงปฏิบัติ นักเรียนจะได้แก้โจทย์ปัญหาหลายขั้นตอนที่เกี่ยวข้องกับรูปสามเหลี่ยม รูปสี่เหลี่ยม วงกลม และรูปสามมิติ พร้อมทั้งพัฒนาความสามารถในการมองเห็นความสัมพันธ์ทางเรขาคณิตและแปลงคำอธิบายเป็นสูตรคำนวณทางคณิตศาสตร์ แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียดและวิธีแก้ปัญหาทีละขั้นตอน ทำให้แบบฝึกหัดเหล่านี้เป็นแหล่งข้อมูลที่มีค่าสำหรับการฝึกฝนด้วยตนเองและการเรียนการสอนในห้องเรียนคณิตศาสตร์ระดับชั้น ม.2
Wayground (เดิมคือ Quizizz) สนับสนุนครูผู้สอนคณิตศาสตร์ด้วยแบบฝึกหัดเรขาคณิตที่สร้างโดยครูจำนวนมาก ซึ่งสามารถค้นหา กรอง และปรับแต่งได้ง่ายเพื่อให้ตรงกับความต้องการของห้องเรียนที่หลากหลาย แพลตฟอร์มนี้มีแหล่งข้อมูลนับล้านรายการ รวมถึงสื่อการเรียนการสอนที่สอดคล้องกับมาตรฐานหลักสูตรคณิตศาสตร์ระดับชั้น ม.2 ช่วยให้ครูสามารถค้นหาเนื้อหาที่เหมาะสมสำหรับการวางแผนบทเรียน การแก้ไขทักษะ และกิจกรรมเสริมสร้างความรู้ได้อย่างรวดเร็ว ครูสามารถเข้าถึงสื่อเหล่านี้ได้ทั้งในรูปแบบ PDF ที่พิมพ์ได้ และในรูปแบบดิจิทัลแบบโต้ตอบ ทำให้สามารถนำไปใช้ได้อย่างยืดหยุ่นในสภาพแวดล้อมการเรียนรู้และวิธีการสอนที่แตกต่างกัน เครื่องมือการปรับระดับความยากง่ายที่ทรงประสิทธิภาพช่วยให้ครูสามารถปรับความซับซ้อนของโจทย์ ปรับจุดเน้นของเนื้อหา และสร้างชุดแบบฝึกหัดที่ตรงเป้าหมายเพื่อแก้ไขช่องว่างการเรียนรู้ของนักเรียนแต่ละคน พร้อมทั้งสร้างความมั่นใจในกลยุทธ์การแก้ปัญหาทางเรขาคณิต
