
15Q
9th

20Q
9th

12Q
9th

6Q
9th

113Q
3rd - Uni
![[Toán 9] Kiểm tra tuần 2 tháng 10 - Imprimible Hợp-lý-hóa-những-người-cấp-tiến Phiếu-bài-tập Lớp 9 - Quizizz](https://quizizz-static.s3.amazonaws.com/_media/worksheets-new/651fe8d2a23f4c3fa6849ea5-[toán-9]-kiểm-tra-tuần-2-tháng-10)
20Q
9th

22Q
9th

21Q
9th
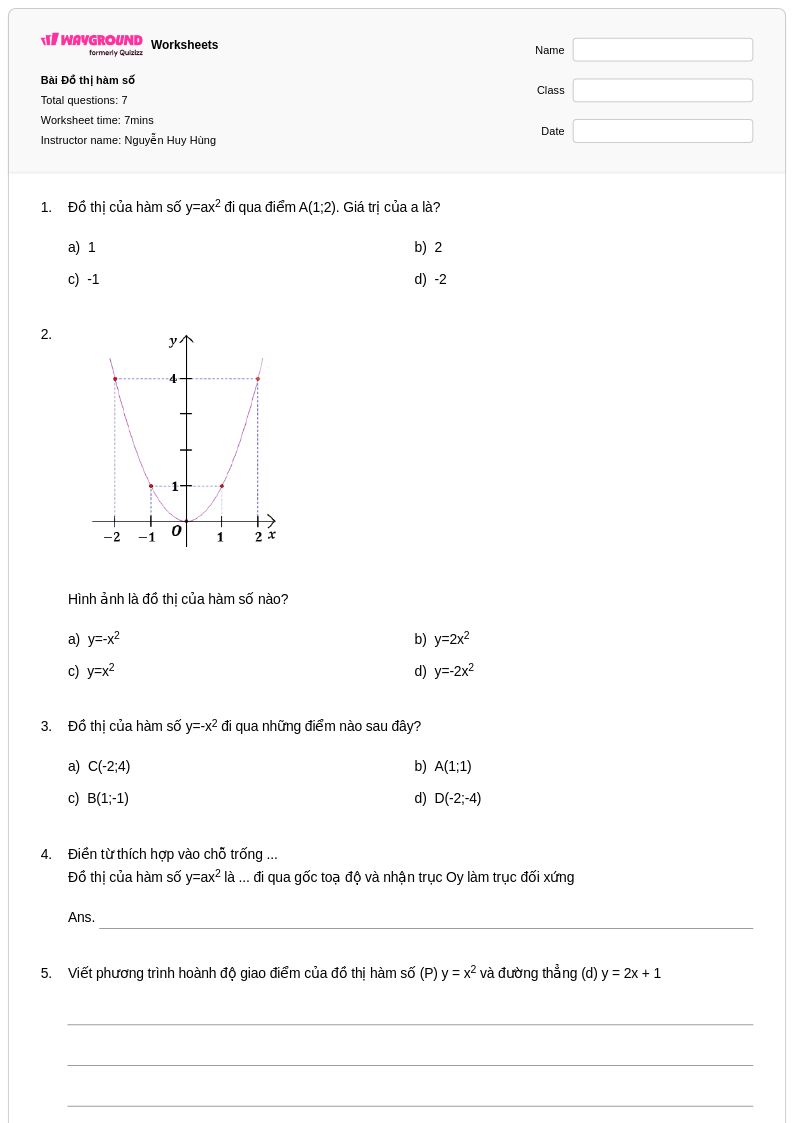
7Q
9th

20Q
7th - 12th

20Q
3rd - Uni

30Q
1st - Uni

10Q
9th

20Q
KG - 10th

10Q
4th - Uni

10Q
4th - Uni

20Q
3rd - Uni

10Q
4th - Uni

282Q
1st - 12th

10Q
9th - 12th
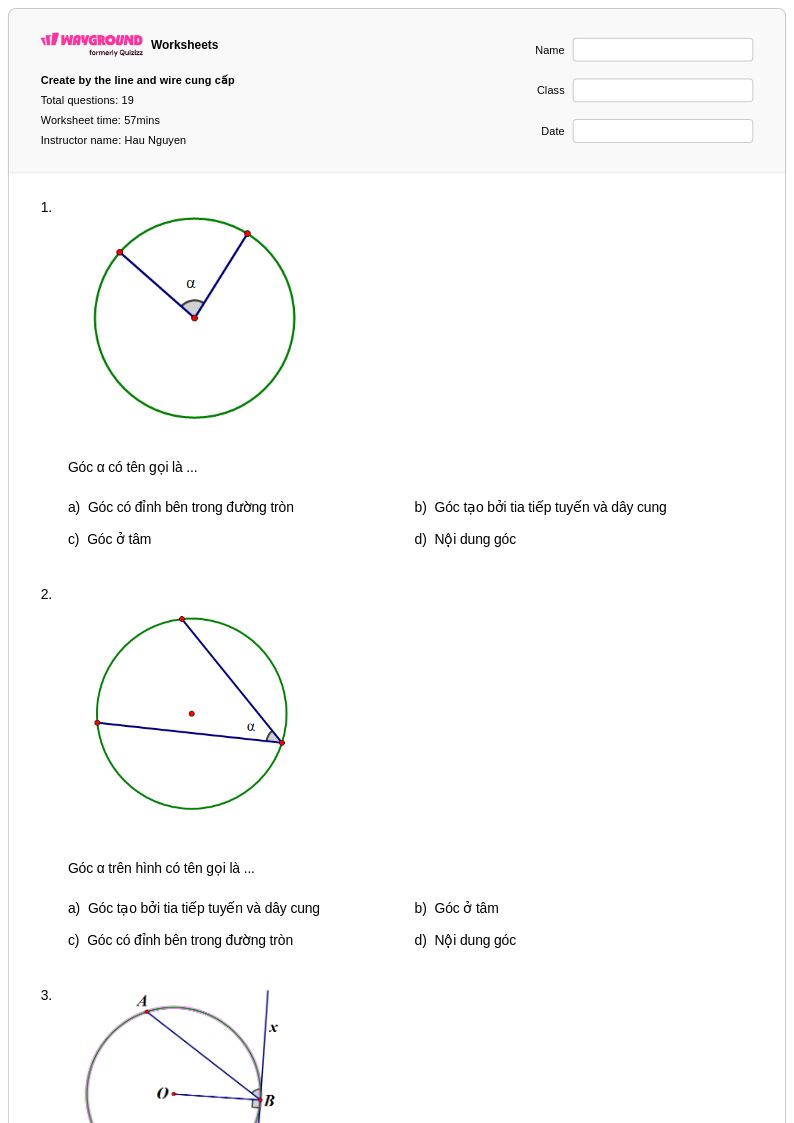
19Q
9th

20Q
3rd - Uni

11Q
1st - Uni

10Q
KG - 10th
Explore otras hojas de trabajo de materias para lớp 9
Khám phá các trang tính Hợp lý hóa những người cấp tiến có thể in được cho Lớp 9
Trục căn thức là một kỹ năng đại số cơ bản mà học sinh lớp 9 cần nắm vững để tự tin tiến bộ trong các môn toán cao cấp hơn. Bộ sưu tập bài tập trục căn thức toàn diện của Wayground cung cấp các bài tập thực hành có cấu trúc với các kỹ thuật thiết yếu bao gồm nhân với số liên hợp, đơn giản hóa biểu thức căn thức ở mẫu số và chuyển đổi mẫu số vô tỷ thành dạng hữu tỷ. Những bài toán thực hành được thiết kế cẩn thận này củng cố sự hiểu biết của học sinh về các tính chất của căn thức đồng thời xây dựng khả năng tính toán thành thạo với các phép toán phân số phức tạp. Mỗi bài tập đều bao gồm đáp án đầy đủ và có sẵn dưới dạng tệp PDF miễn phí để tải xuống, giúp các nhà giáo dục dễ dàng cung cấp sự củng cố kỹ năng có mục tiêu thông qua các bài tập in được nhằm giải quyết các quan niệm sai lầm phổ biến và các lỗi về quy trình.
Thư viện rộng lớn của Wayground, được xây dựng từ hàng triệu tài nguyên do giáo viên tạo ra, cung cấp cho các nhà giáo dục những công cụ mạnh mẽ để phân biệt việc giảng dạy trục căn thức cho học sinh lớp 9 đa dạng. Khả năng tìm kiếm và lọc nâng cao của nền tảng cho phép giáo viên nhanh chóng tìm thấy các bài tập phù hợp với các tiêu chuẩn chương trình giảng dạy và mức độ khó cụ thể, trong khi các tính năng tùy chỉnh cho phép sửa đổi các tài liệu hiện có để phù hợp với nhu cầu của từng lớp học. Các tài liệu này có sẵn ở cả định dạng PDF có thể in và phiên bản kỹ thuật số tương tác, hỗ trợ việc lập kế hoạch bài học linh hoạt cho dù là giảng dạy toàn lớp, ôn tập nhóm nhỏ hay các hoạt động nâng cao độc lập. Giáo viên có thể hỗ trợ việc học của học sinh một cách hiệu quả bằng cách lựa chọn từ các bài tập được sắp xếp một cách có hệ thống, từ việc đơn giản hóa căn bậc hai cơ bản đến việc khử căn bậc hai phức tạp hơn liên quan đến mẫu số nhị thức và căn bậc hai bậc cao hơn.
