
18 Q
4th

19 Q
4th - 7th

22 Q
1st - 3rd

10 Q
4th

20 Q
4th - 5th

20 Q
4th

21 Q
4th

20 Q
8th

7 Q
5th

6 Q
11th

12 Q
2nd
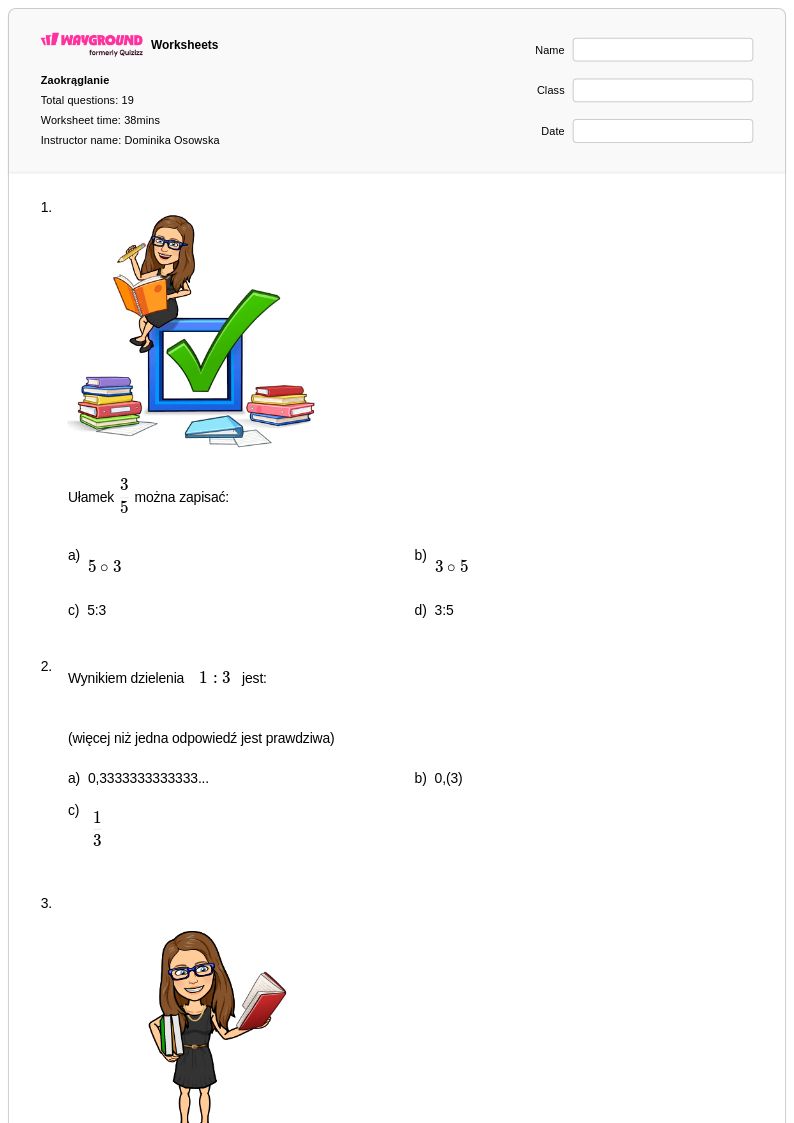
19 Q
5th - 6th

16 Q
8th

14 Q
4th - 5th

8 Q
1st - 3rd

17 Q
8th

24 Q
5th

13 Q
1st - 5th

20 Q
6th

20 Q
1st

10 Q
1st - 6th
11 Q
2nd - 6th

9 Q
4th

8 Q
3rd - 4th
Explore Worksheets by Subjects
Przeglądaj arkusze robocze Dzielenie radykałów do wydrukowania
Arkusze ćwiczeń z pierwiastków dzielonych dostępne w Wayground (dawniej Quizizz) zapewniają uczniom wszechstronne możliwości praktycznego opanowania tej fundamentalnej umiejętności algebraicznej. Te starannie zaprojektowane zasoby koncentrują się na podstawowych technikach, takich jak racjonalizowanie mianowników, upraszczanie wyrażeń pierwiastkowych za pomocą współczynników oraz stosowanie reguły ilorazu dla pierwiastków. Uczniowie pracują nad systematycznymi zadaniami praktycznymi, które stopniowo budują ich wiedzę na temat dzielenia pierwiastków kwadratowych, sześciennych i pierwiastków wyższego rzędu, zachowując jednocześnie matematyczną dokładność. Każdy zbiór arkuszy ćwiczeń zawiera szczegółowe klucze odpowiedzi i rozwiązania krok po kroku, dzięki czemu te bezpłatne materiały do druku w formacie PDF są nieocenione zarówno do samodzielnej nauki, jak i do nauczania w klasie.
Wayground (dawniej Quizizz) oferuje nauczycielom matematyki bogatą bibliotekę milionów stworzonych przez nich arkuszy ćwiczeń z pierwiastków dzielonych, które usprawniają planowanie lekcji i zróżnicowane nauczanie. Rozbudowane funkcje wyszukiwania i filtrowania platformy pozwalają nauczycielom szybko znaleźć zasoby dostosowane do określonych standardów matematycznych i poziomów umiejętności, zapewniając odpowiedni poziom trudności dla zróżnicowanych uczniów. Nauczyciele mogą bezproblemowo dostosowywać istniejące arkusze ćwiczeń lub tworzyć nowe wersje, aby sprostać indywidualnym potrzebom uczniów, zarówno w celu utrwalenia podstawowych pojęć radykalnych, jak i w celu wzbogacenia materiału o złożone wyrażenia radykalne. Te wszechstronne zasoby są dostępne zarówno w formacie do druku, jak i cyfrowym, co umożliwia elastyczne wdrażanie w tradycyjnych i wspomaganych technologicznie środowiskach edukacyjnych, a jednocześnie wspiera systematyczny rozwój umiejętności i ocenę w zakresie rozwiązywania problemów algebraicznych.
