
8Q
1st - 5th

14Q
1st - 7th

18Q
1st - 5th

16Q
3rd

11Q
1st - 5th

15Q
1st - 6th

7Q
1st - 6th

10Q
1st - 6th
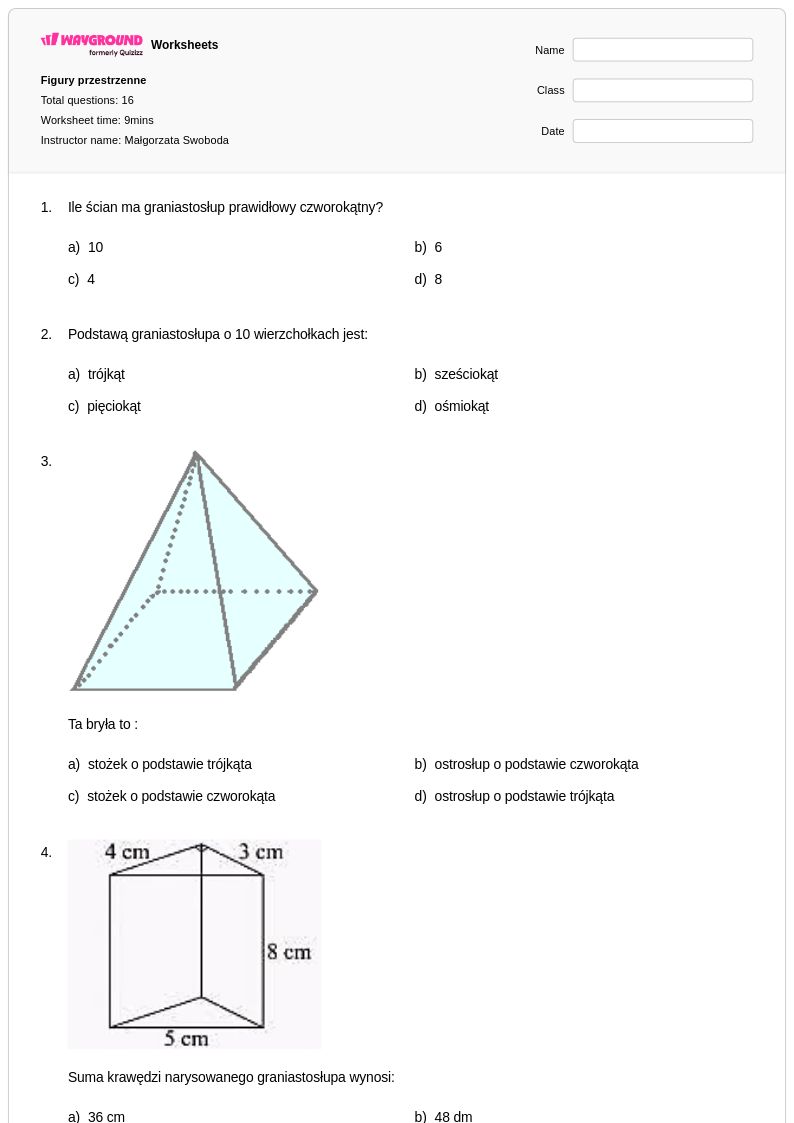
16Q
2nd - 5th

10Q
1st - 5th

6Q
1st - 6th

12Q
1st - 6th
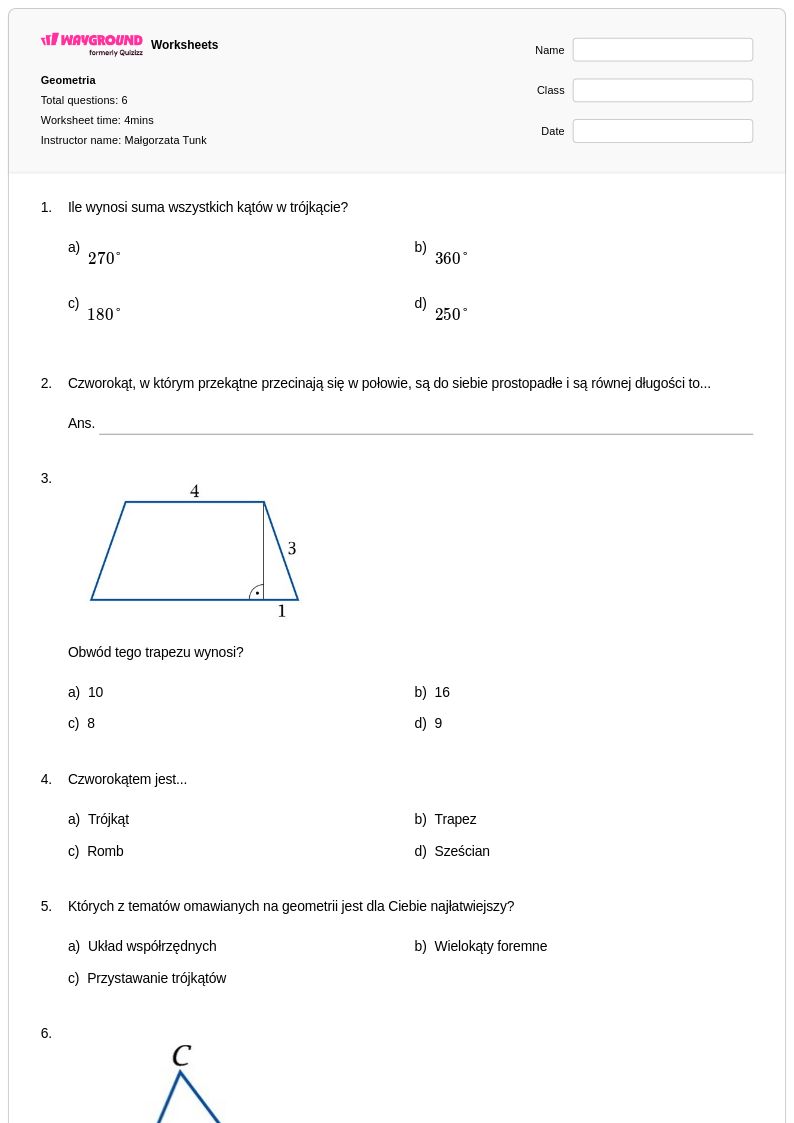
6Q
1st - 6th
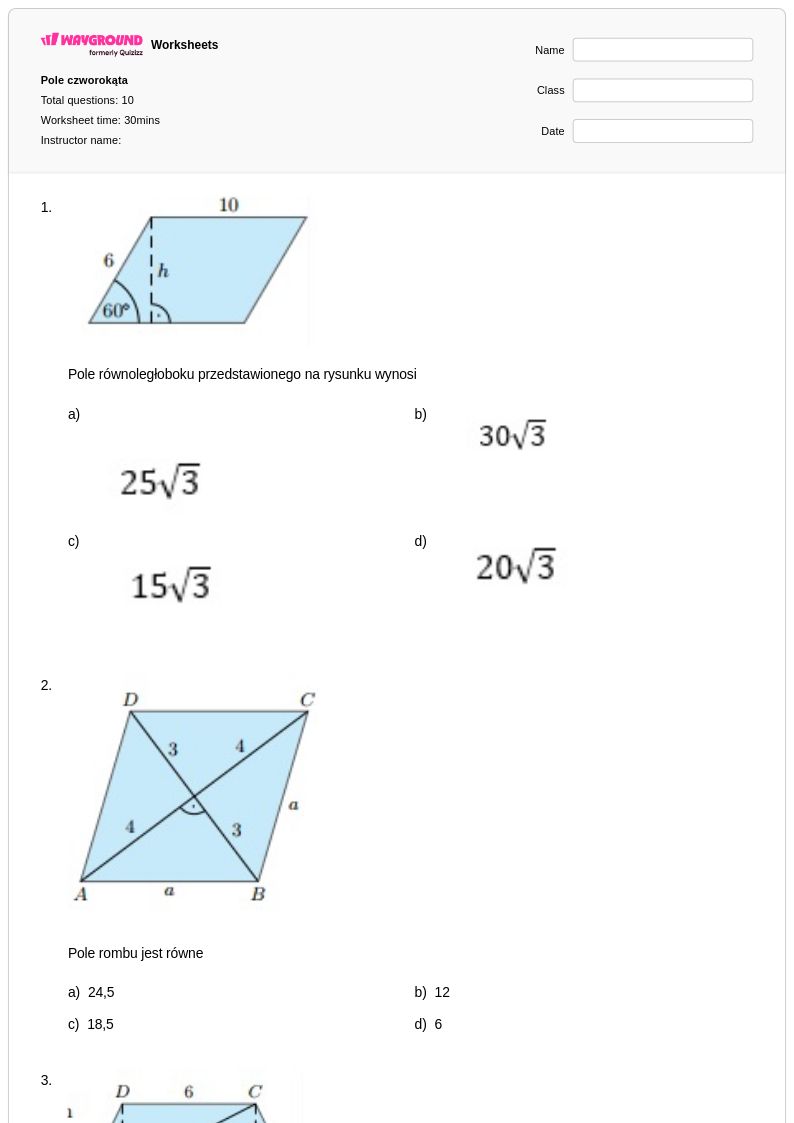
10Q
1st - 5th

18Q
1st - 6th
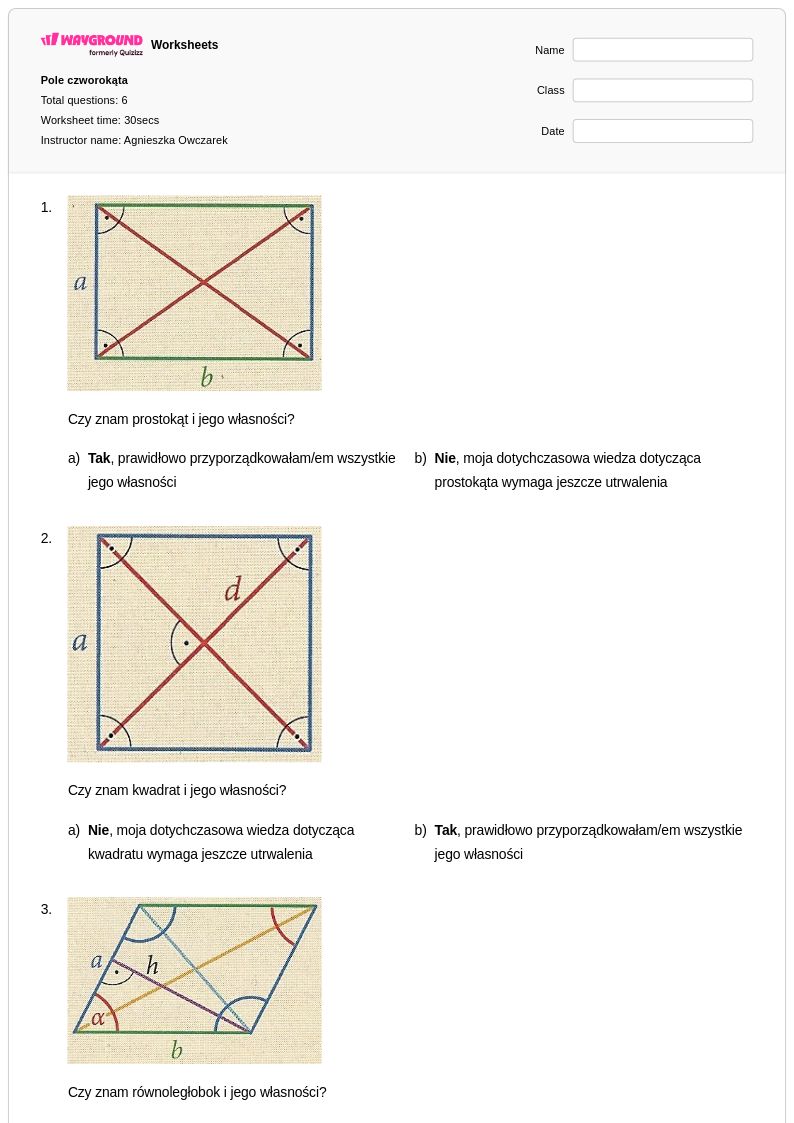
6Q
3rd

7Q
1st - 4th
15Q
1st - 6th

7Q
1st - 5th

15Q
1st - 12th

21Q
1st - 6th

10Q
1st - 5th
18Q
1st - 5th

19Q
1st - 5th
Explore otras hojas de trabajo de materias para klasa 3
Przeglądaj arkusze Pole trapezu do wydrukowania dla Klasa 3
Arkusze ćwiczeń z pola trapezu dla klasy 3, dostępne w Wayground (dawniej Quizizz), zapewniają niezbędne ćwiczenia praktyczne dla uczniów uczących się obliczania objętości wewnątrz czworokątów o jednej parze boków równoległych. Te kompleksowe arkusze ćwiczeń wzmacniają podstawowe umiejętności geometryczne, prowadząc uczniów przez metody rozwiązywania problemów krok po kroku, pomagając im zrozumieć, jak identyfikować równoległe podstawy, mierzyć wysokości i stosować wzór na pole trapezu w kontekście odpowiednim do wieku. Każdy zbiór arkuszy ćwiczeń zawiera szczegółowe klucze odpowiedzi i jest dostępny w wygodnym formacie PDF, oferując bezpłatne materiały do wydruku, które zawierają starannie opracowane zadania praktyczne, od podstawowej identyfikacji trapezów po bardziej złożone obliczenia pola powierzchni z wykorzystaniem prostych liczb całkowitych, odpowiednie dla uczniów klasy 3.
Wayground (dawniej Quizizz) oferuje nauczycielom bogatą bibliotekę milionów zasobów stworzonych przez nauczycieli, specjalnie zaprojektowanych do wspierania nauczania pola trapezu na poziomie klasy 3. Rozbudowane funkcje wyszukiwania i filtrowania platformy pozwalają nauczycielom szybko znaleźć arkusze ćwiczeń zgodne ze standardami matematycznymi i dopasowane do specyficznych potrzeb klasy, a wbudowane narzędzia różnicujące umożliwiają dostosowanie do różnych poziomów nauczania w ramach tej samej klasy. Te elastyczne zasoby są dostępne zarówno w formatach PDF do druku, jak i w interaktywnych wersjach cyfrowych, co czyni je nieocenionymi w planowaniu lekcji, ukierunkowanych działaniach korepetycyjnych dla uczniów mających trudności, zajęciach wzbogacających dla uczniów zaawansowanych oraz w regularnym ćwiczeniu umiejętności, które utrwalają pojęcia geometryczne poprzez powtarzalne zastosowania i wizualne strategie uczenia się.
