
13 P
5th - 10th

20 P
6th

11 P
8th

7 P
5th

9 P
5th
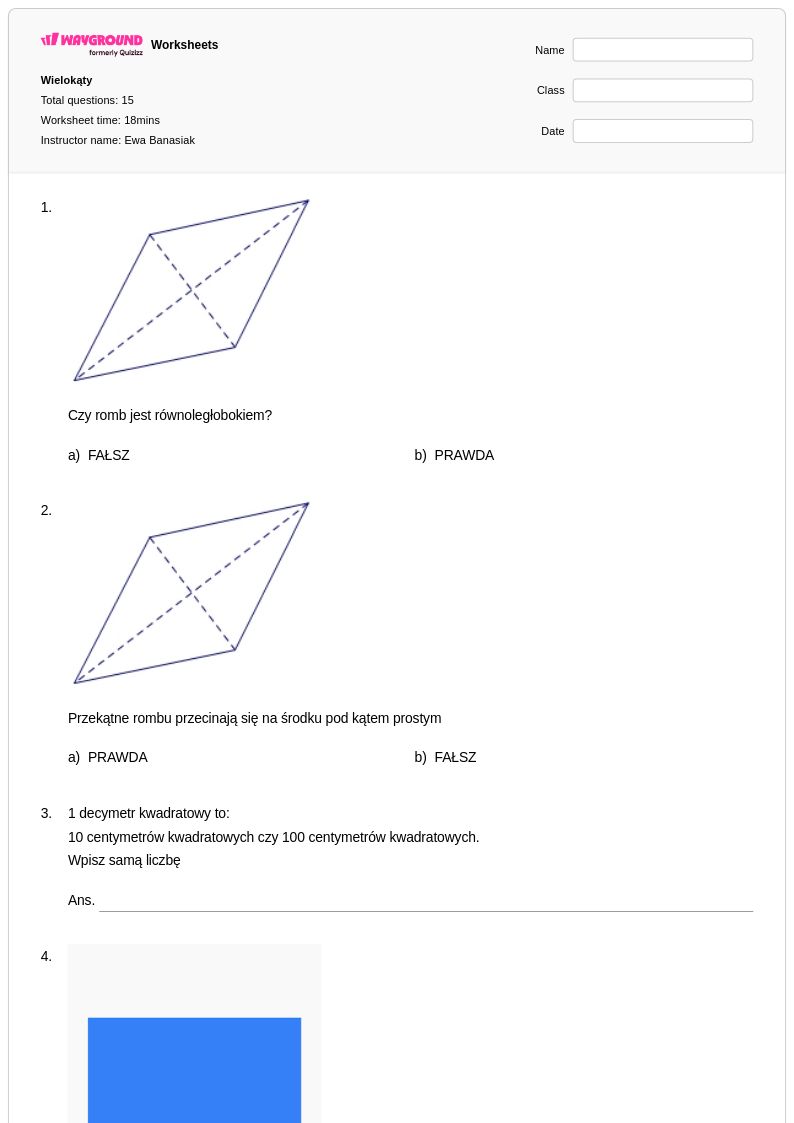
15 P
5th

16 P
KG

30 P
6th
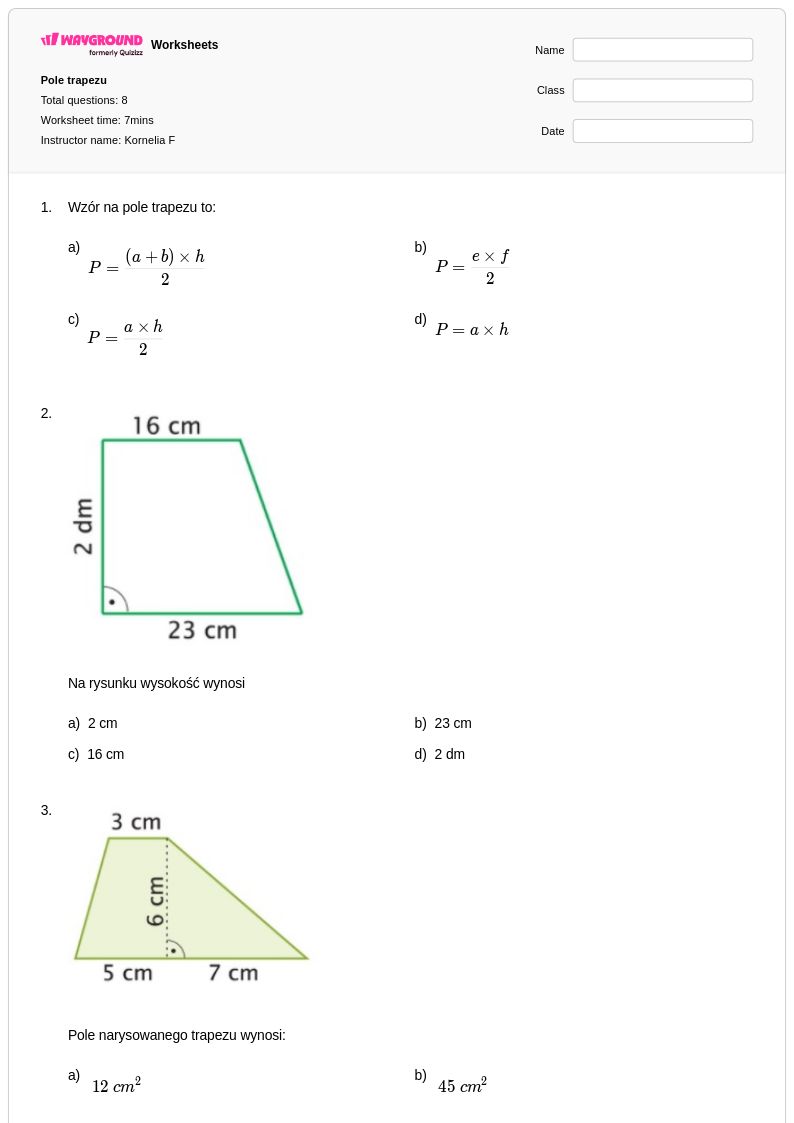
8 P
5th - Uni

14 P
6th

14 P
7th

12 P
5th

6 P
5th - 8th
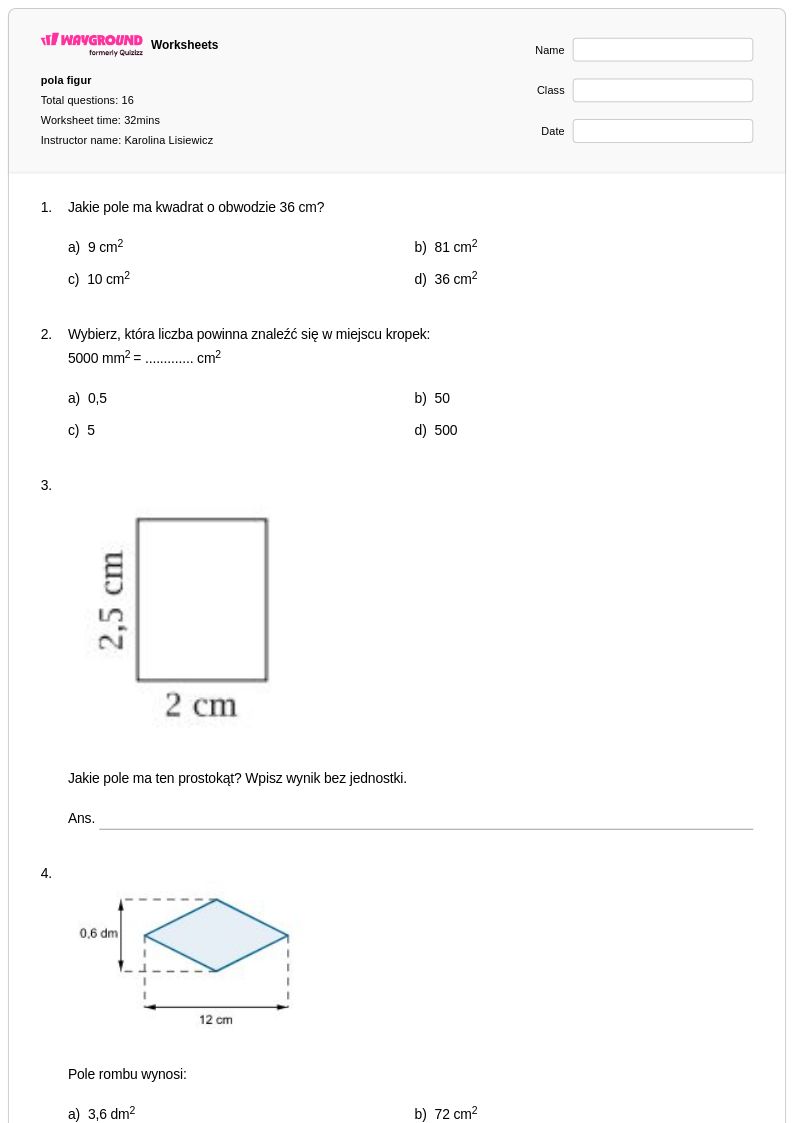
16 P
7th

12 P
1st - 4th
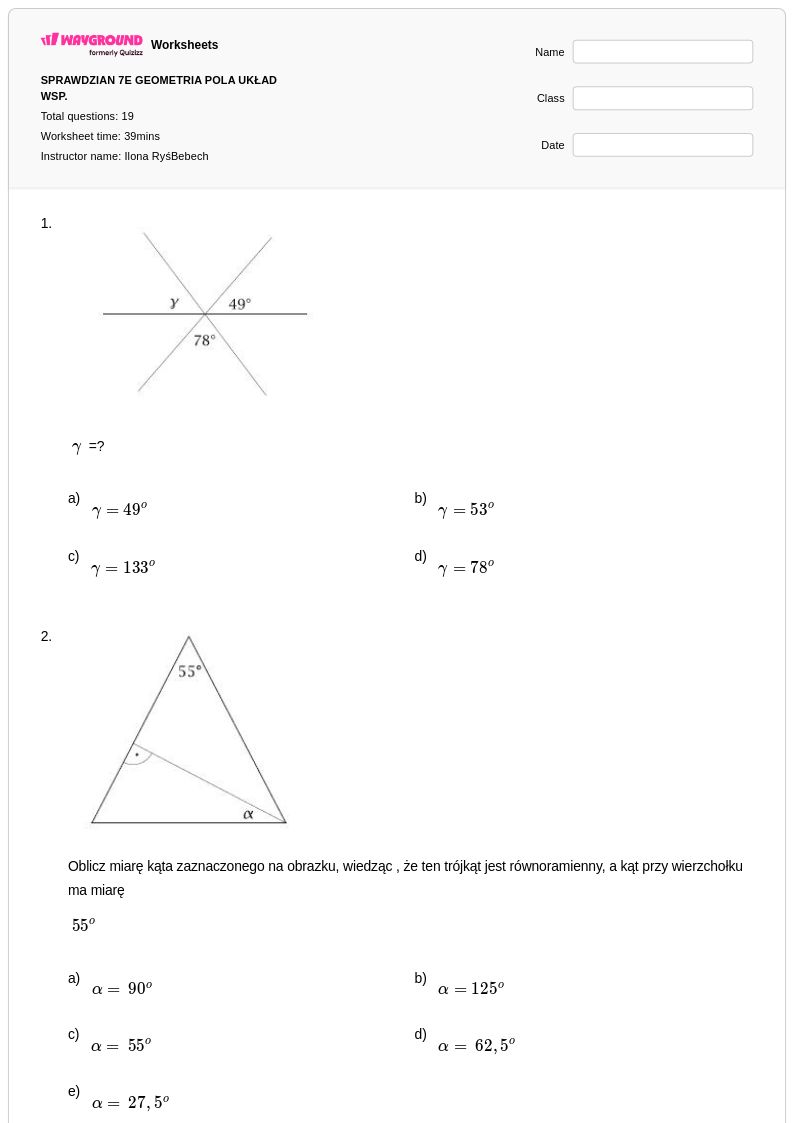
19 P
7th - 8th

20 P
6th

16 P
5th

15 P
5th
10 P
5th

13 P
6th
13 P
6th

16 P
KG - PD
15 P
7th
Przeglądaj arkusze według tematów
Przeglądaj arkusze robocze Pole trapezu do wydrukowania
Arkusze ćwiczeń z pola trapezu dostępne w Wayground (dawniej Quizizz) zapewniają uczniom wszechstronne możliwości praktycznego opanowania tego podstawowego obliczenia geometrycznego. Te profesjonalnie zaprojektowane zasoby koncentrują się na rozwijaniu umiejętności stosowania wzoru na pole trapezu, który wymaga od uczniów identyfikowania boków równoległych, mierzenia wysokości i wykonywania dokładnych obliczeń z wykorzystaniem równania A = ½(a + b)h. Zbiory arkuszy ćwiczeń wzmacniają kluczowe umiejętności matematyczne, takie jak stosowanie wzorów, interpretacja pomiarów i manipulacje algebraiczne, jednocześnie budując zrozumienie pojęciowe związku własności trapezu z obliczeniami pola. Każdy zasób zawiera szczegółowe klucze odpowiedzi i rozwiązania krok po kroku, a wiele z nich jest dostępnych w postaci darmowych plików PDF do wydruku, które nauczyciele mogą bezproblemowo włączyć do programu nauczania geometrii, aby rozwiązywać konkretne zadania praktyczne i utrwalać umiejętności.
Wayground (dawniej Quizizz) udostępnia nauczycielom bogatą bibliotekę milionów arkuszy ćwiczeń z pola trapezu stworzonych przez nauczycieli, które usprawniają nauczanie i ocenę geometrii. Rozbudowane funkcje wyszukiwania i filtrowania platformy pozwalają nauczycielom szybko znaleźć zasoby zgodne z określonymi standardami matematycznymi i celami nauczania, a wbudowane narzędzia różnicujące pozwalają na dostosowanie do zróżnicowanych potrzeb i poziomów umiejętności uczniów. Te elastyczne zbiory arkuszy ćwiczeń są dostępne zarówno w formacie do druku, jak i cyfrowym, w tym w formacie PDF do pobrania, dzięki czemu idealnie nadają się do nauczania w klasie, zadań domowych, sesji naprawczych i zajęć dodatkowych. Nauczyciele mogą sprawnie modyfikować zadania, dostosowywać poziomy trudności i tworzyć ukierunkowane zestawy ćwiczeń, które wspierają postępy poszczególnych uczniów, zarówno utrwalając podstawowe pojęcia dotyczące trapezów, jak i stawiając przed zaawansowanymi uczniami wyzwanie w postaci skomplikowanych, wieloetapowych obliczeń pola powierzchni.
