
19 P
10th - 12th
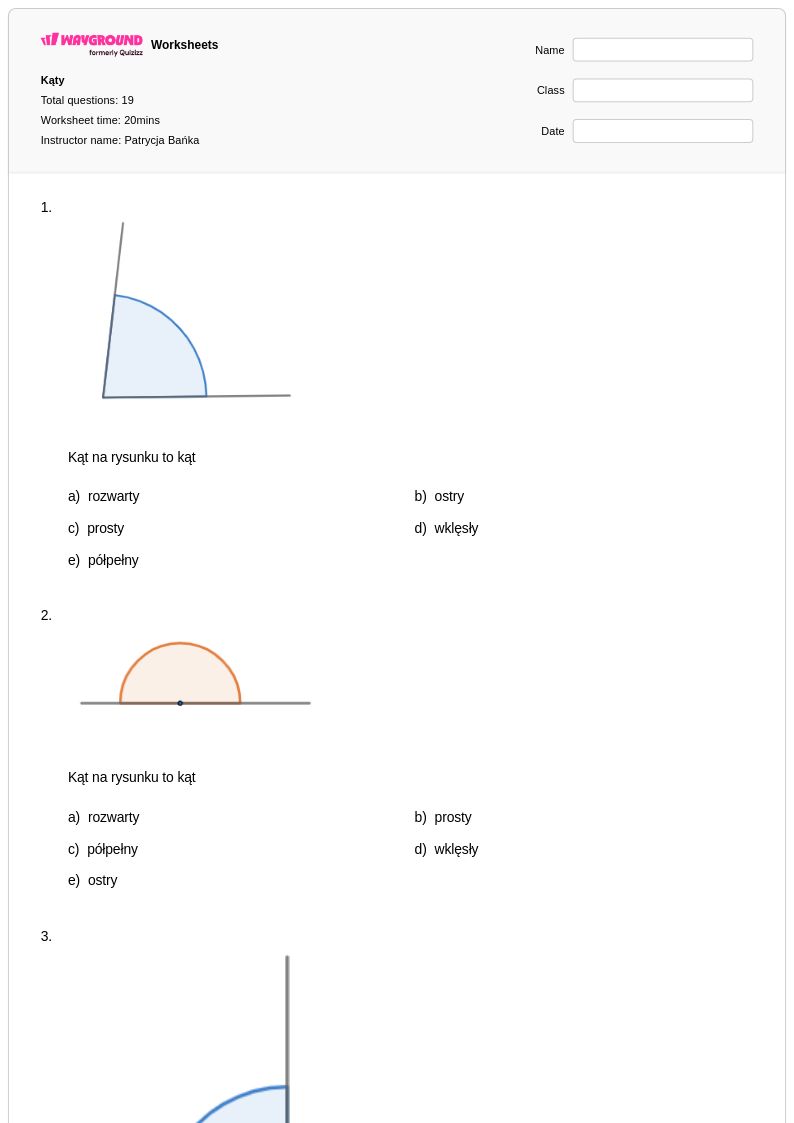
19 P
5th
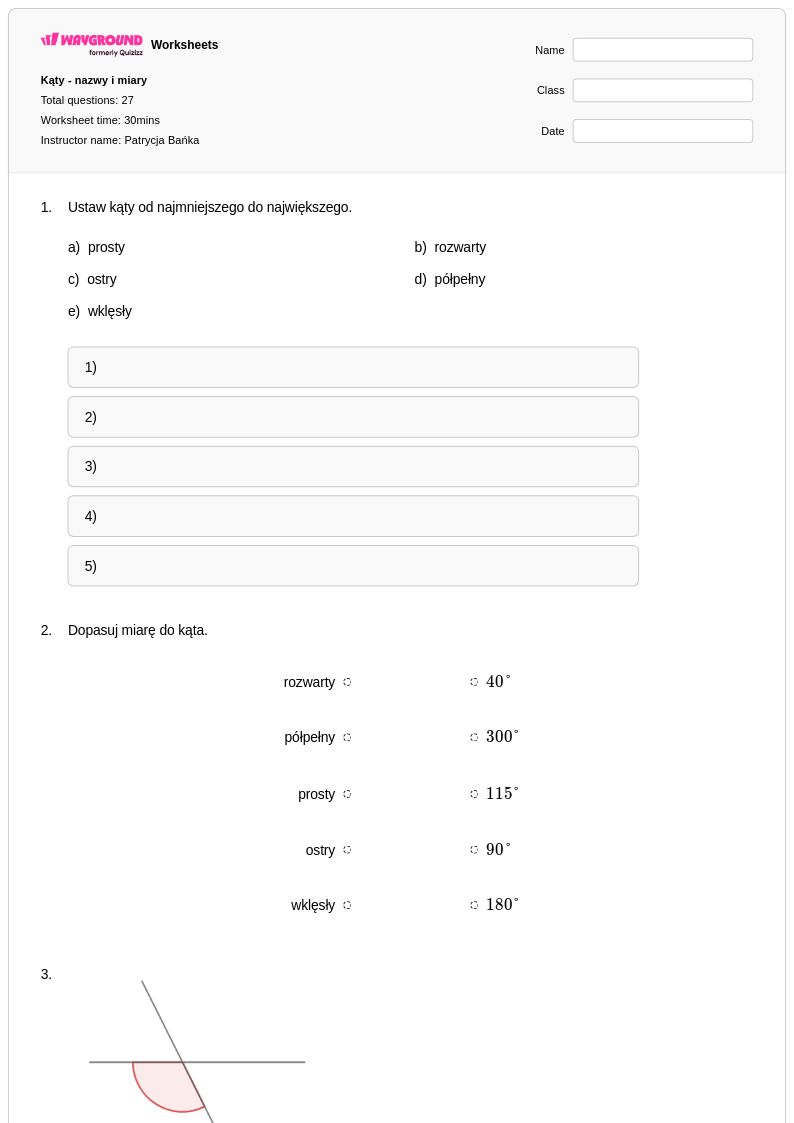
27 P
6th

10 P
2nd
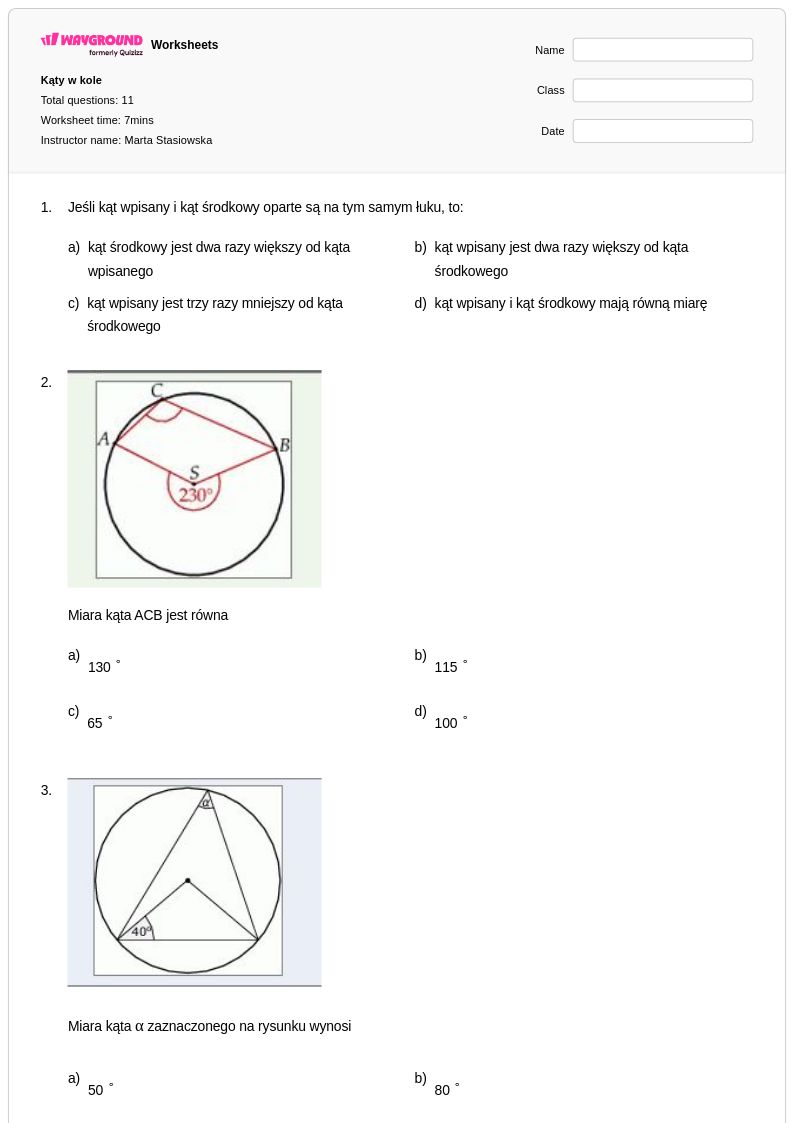
11 P
10th - 12th

21 P
9th - 12th

17 P
4th
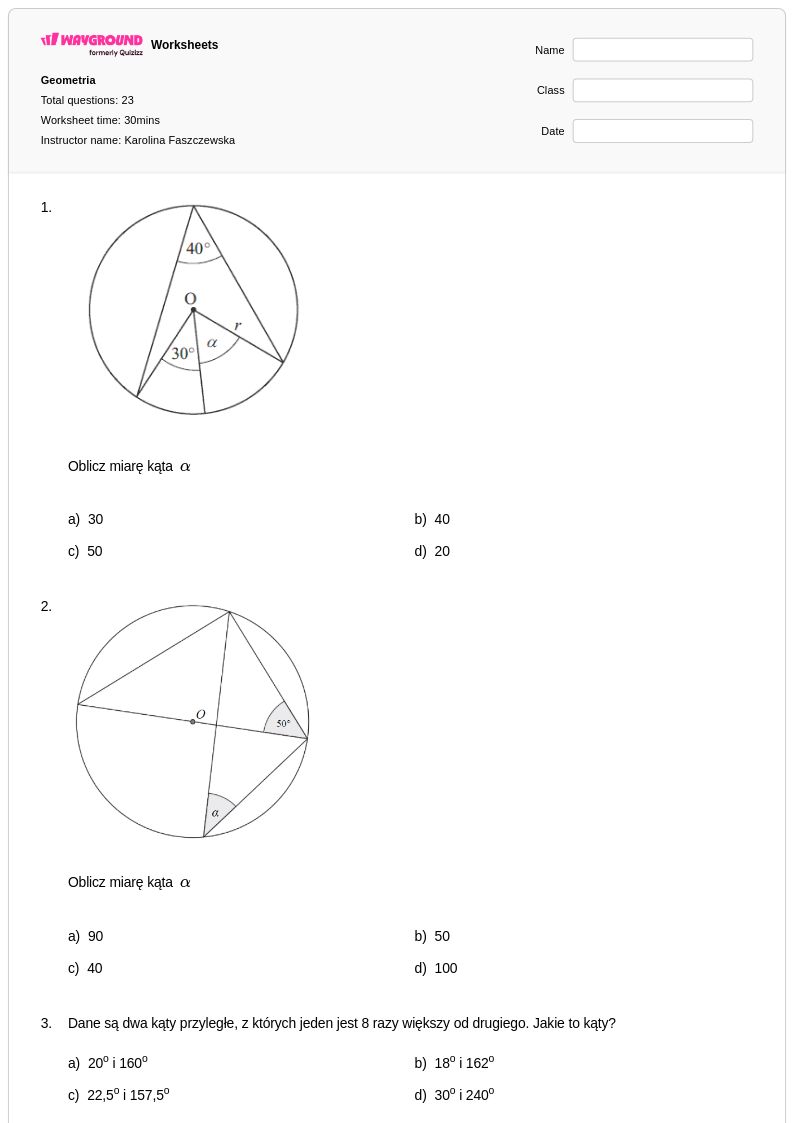
23 P
10th
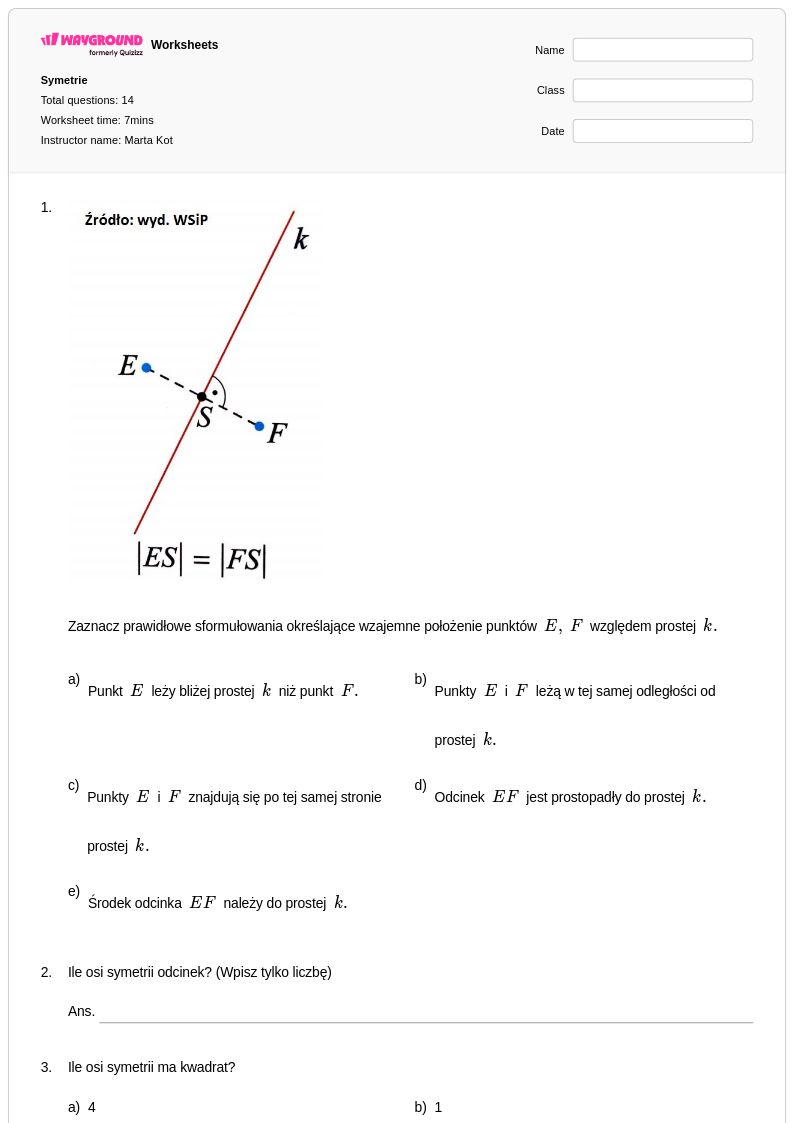
14 P
8th

16 P
7th
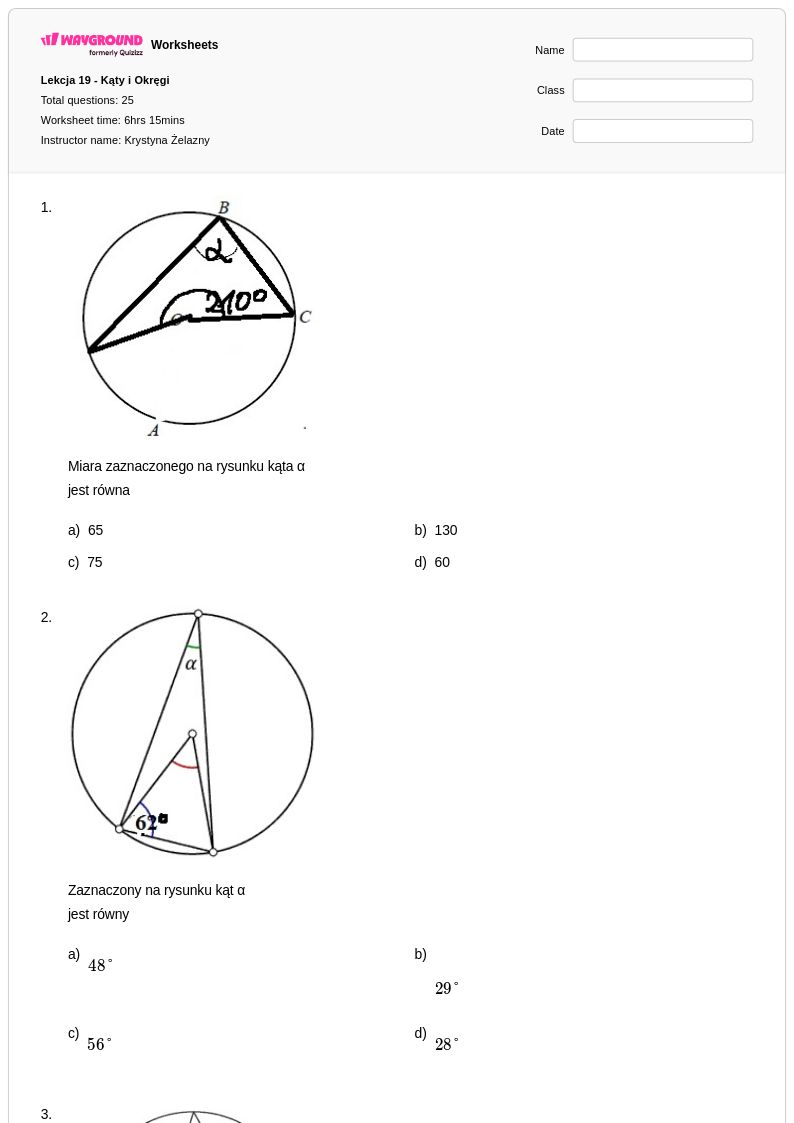
25 P
12th
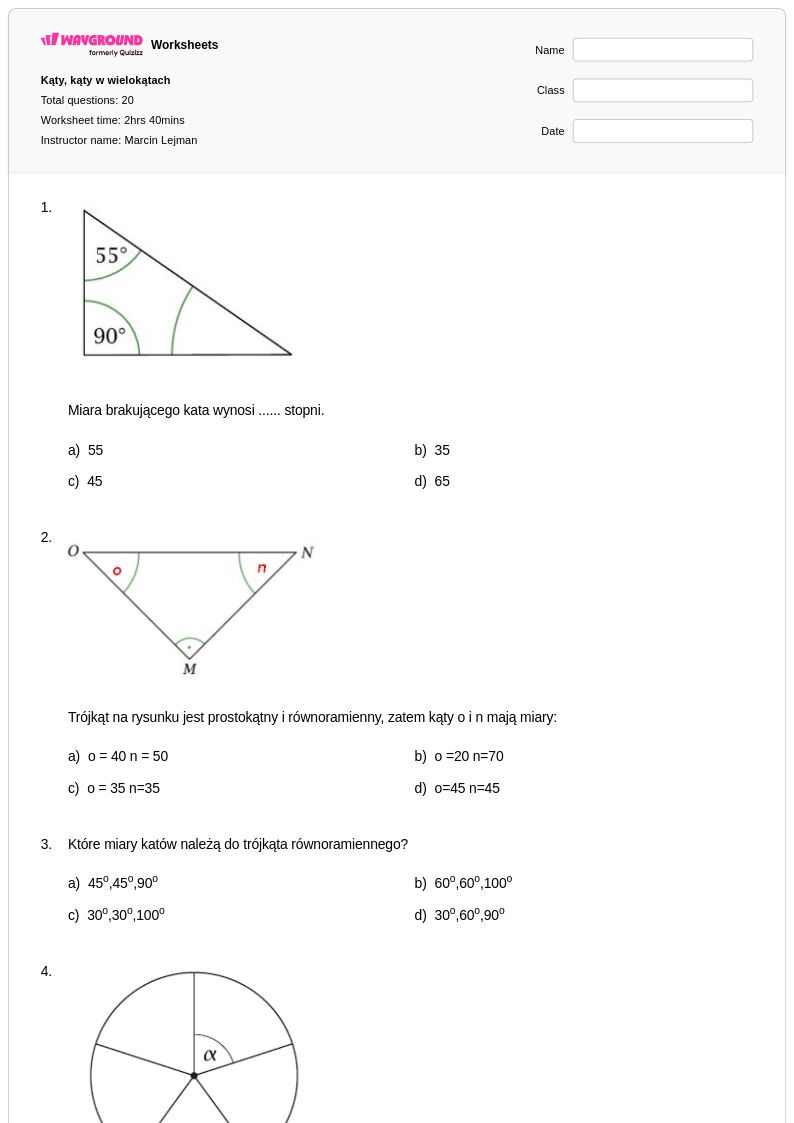
20 P
7th
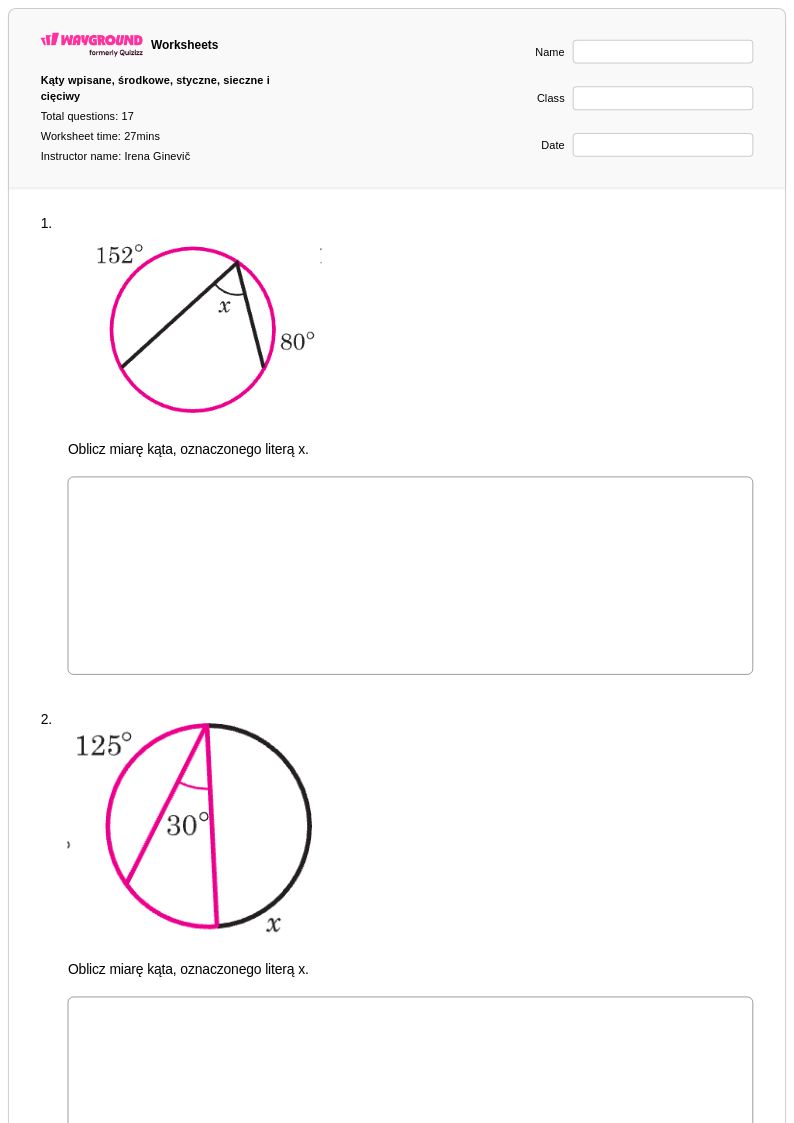
17 P
9th

23 P
12th
22 P
7th
12 P
5th - 6th

15 P
5th
8 P
1st

18 P
5th

20 P
5th

15 P
1st

19 P
7th
20 P
5th
20 P
1st
Przeglądaj arkusze według tematów
Przeglądaj arkusze robocze Kąty wpisane do wydrukowania
Arkusze ćwiczeń dotyczące kątów wpisanych dostępne w Wayground (dawniej Quizizz) dostarczają kompleksowych materiałów ćwiczeniowych, które pomagają uczniom opanować tę fundamentalną koncepcję geometrii. Arkusze te koncentrują się na rozwijaniu u uczniów rozumienia kątów utworzonych przez dwie cięciwy przecinające się na okręgu, wzmacniając ich umiejętność obliczania miar kątów za pomocą twierdzenia o kącie wpisanym i powiązanych własności. Zadania praktyczne prowadzą uczniów przez różne scenariusze obejmujące kąty wpisane, kąty środkowe i łuki, budując biegłość w rozpoznawaniu tych zależności w geometrii okręgu. Każdy arkusz ćwiczeń zawiera szczegółowe klucze odpowiedzi, które wspierają samodzielną naukę i samoocenę, a darmowy format do druku w formacie PDF sprawia, że zasoby te są łatwo dostępne do wykorzystania w klasie i do zadań domowych.
Wayground (dawniej Quizizz) wspiera nauczycieli matematyki bogatą kolekcją arkuszy ćwiczeń dotyczących kątów wpisanych, stworzonych przez nauczycieli i zaczerpniętych z milionów zasobów edukacyjnych. Zaawansowane funkcje wyszukiwania i filtrowania platformy pozwalają nauczycielom szybko znaleźć materiały zgodne z określonymi standardami programowymi i dopasowane do poziomu umiejętności ich uczniów. Te narzędzia różnicujące pozwalają nauczycielom dostosowywać poziom trudności arkuszy ćwiczeń i obszary tematyczne, zapewniając odpowiedni poziom trudności w ramach zajęć korekcyjnych, standardowych ćwiczeń lub zajęć wzbogacających. Elastyczne opcje formatu obejmują zarówno wersje PDF do druku, przeznaczone do tradycyjnej pracy na papierze i ołówku, jak i formaty cyfrowe, które płynnie integrują się z nowoczesną technologią nauczania, zapewniając nauczycielom wszechstronność niezbędną do efektywnego nauczania geometrii i kompleksowego planowania lekcji w zakresie twierdzeń o okręgach i zależnościach kątowych.
