
10 P
Uni - University

15 P
8th

10 P
8th

19 P
9th - 12th

10 P
7th - 8th
20 P
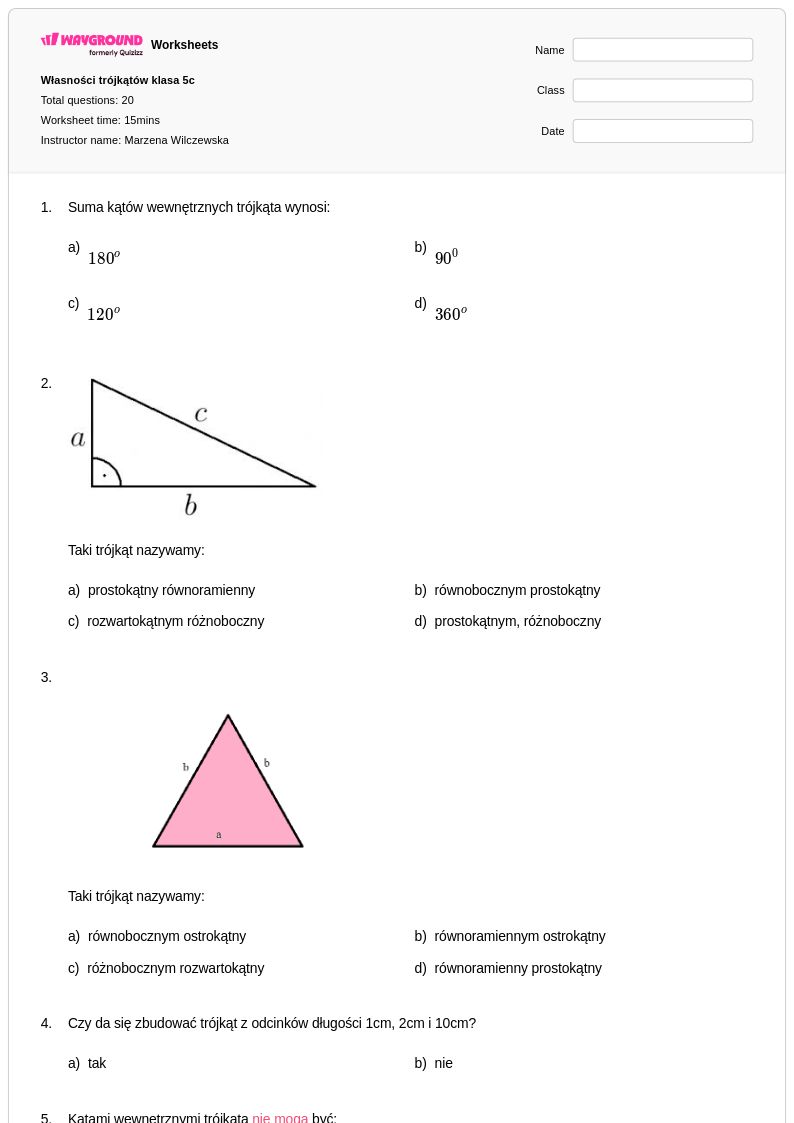
5th

18 P
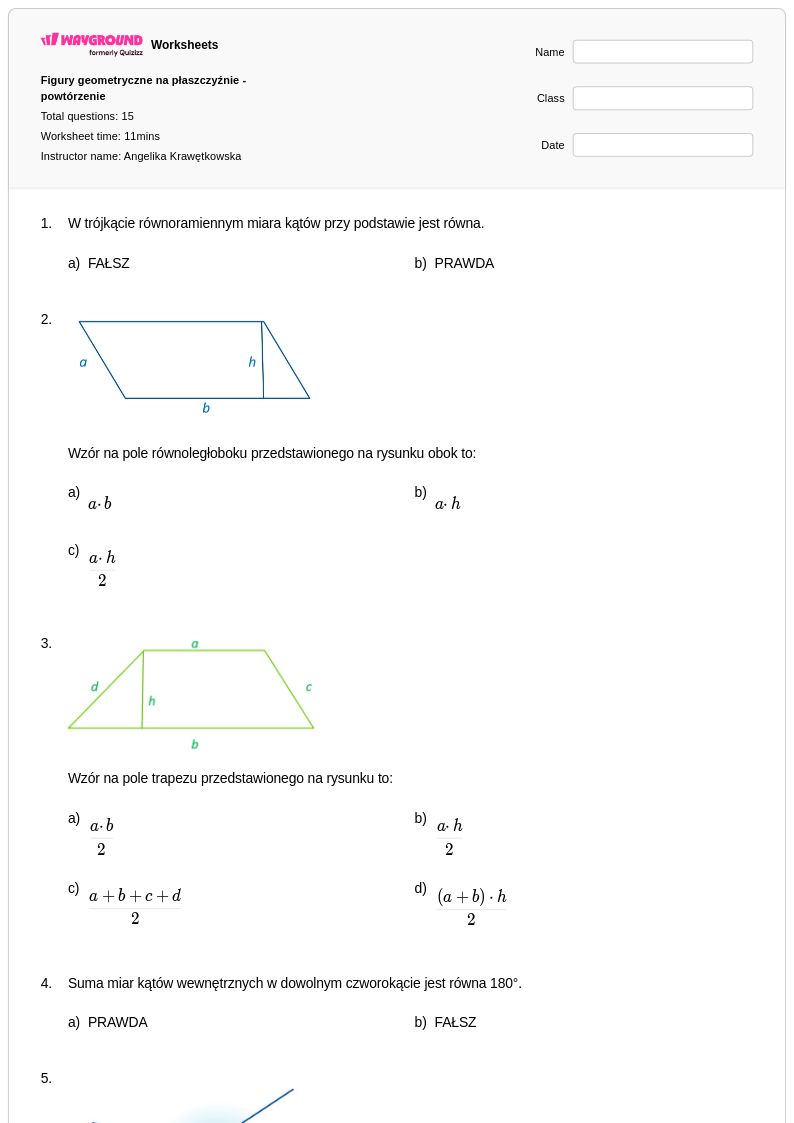
7th - 8th
15 P
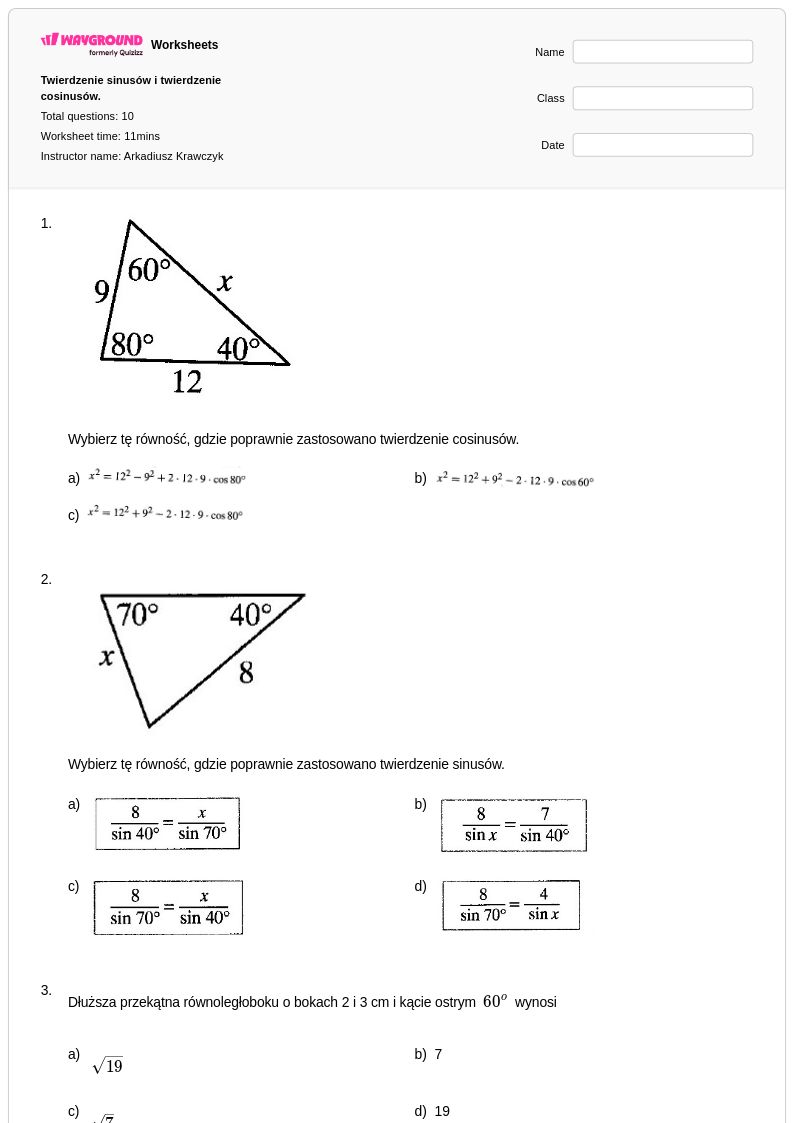
8th
10 P
KG

20 P
1st - 5th

20 P
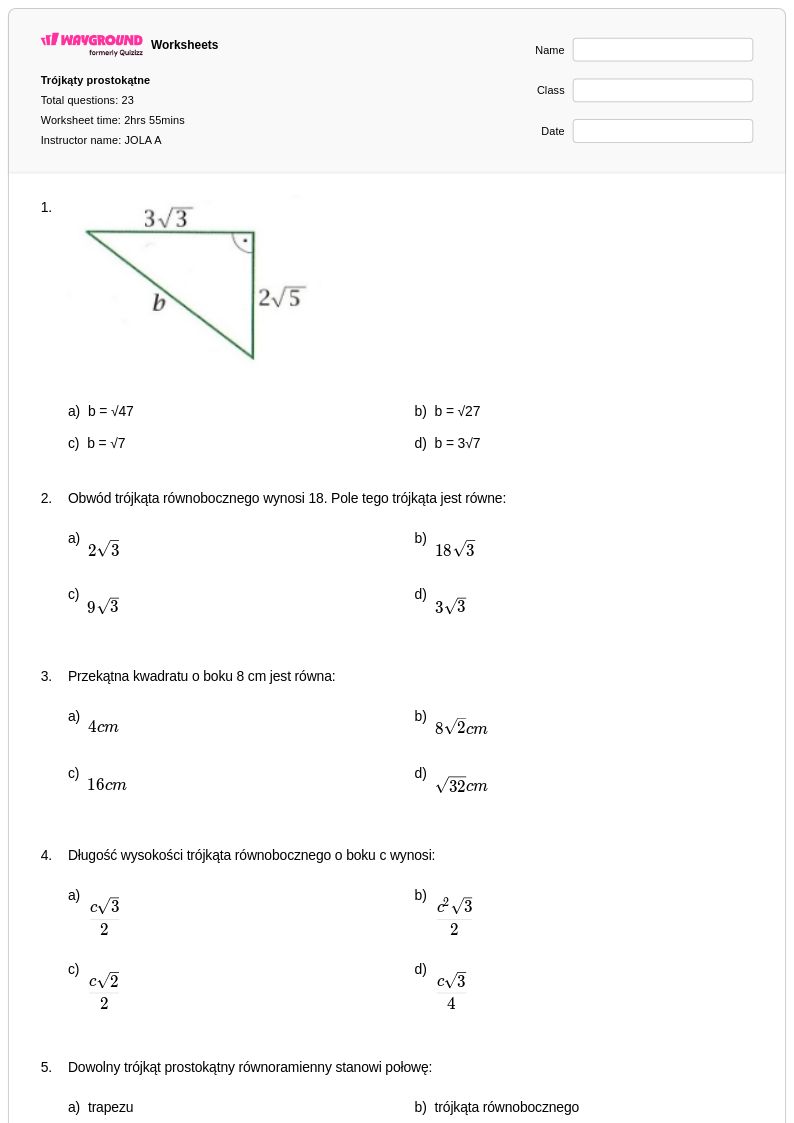
5th
23 P
7th

16 P
6th

25 P
3rd - 8th

14 P
6th

20 P
7th
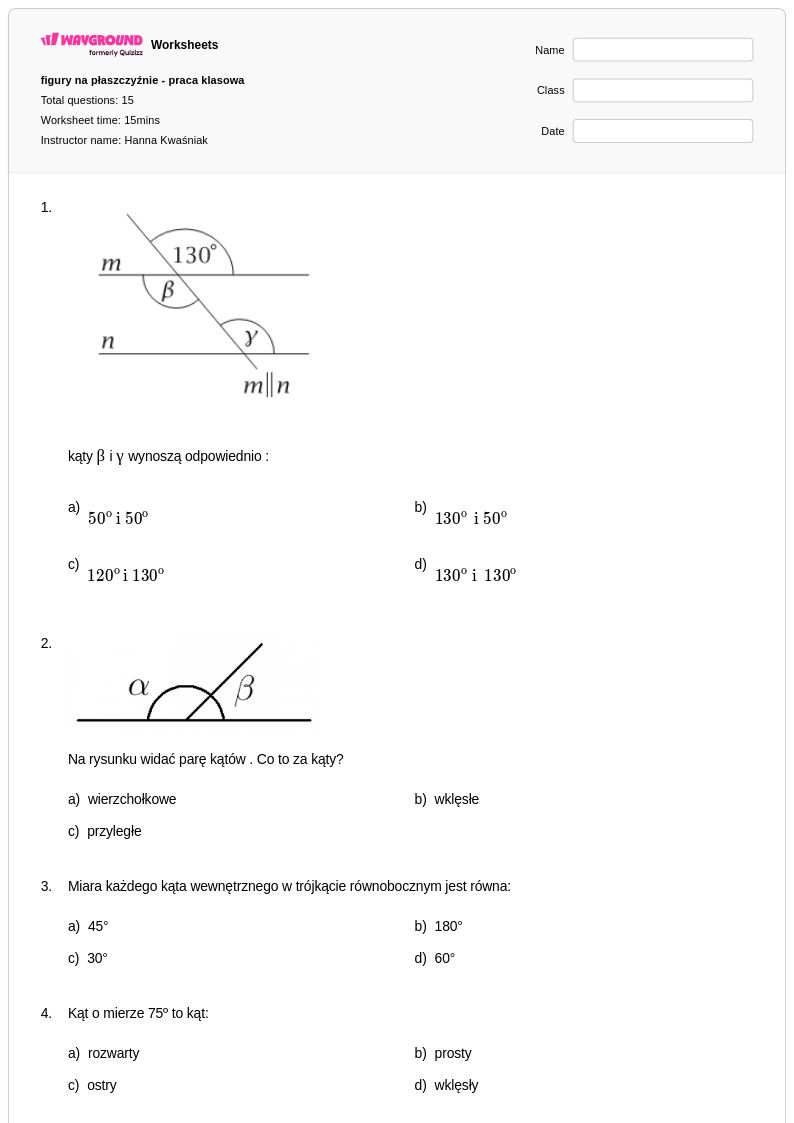
15 P
5th

15 P
7th

10 P
7th

24 P
6th

15 P
5th - 6th

13 P
1st - 5th
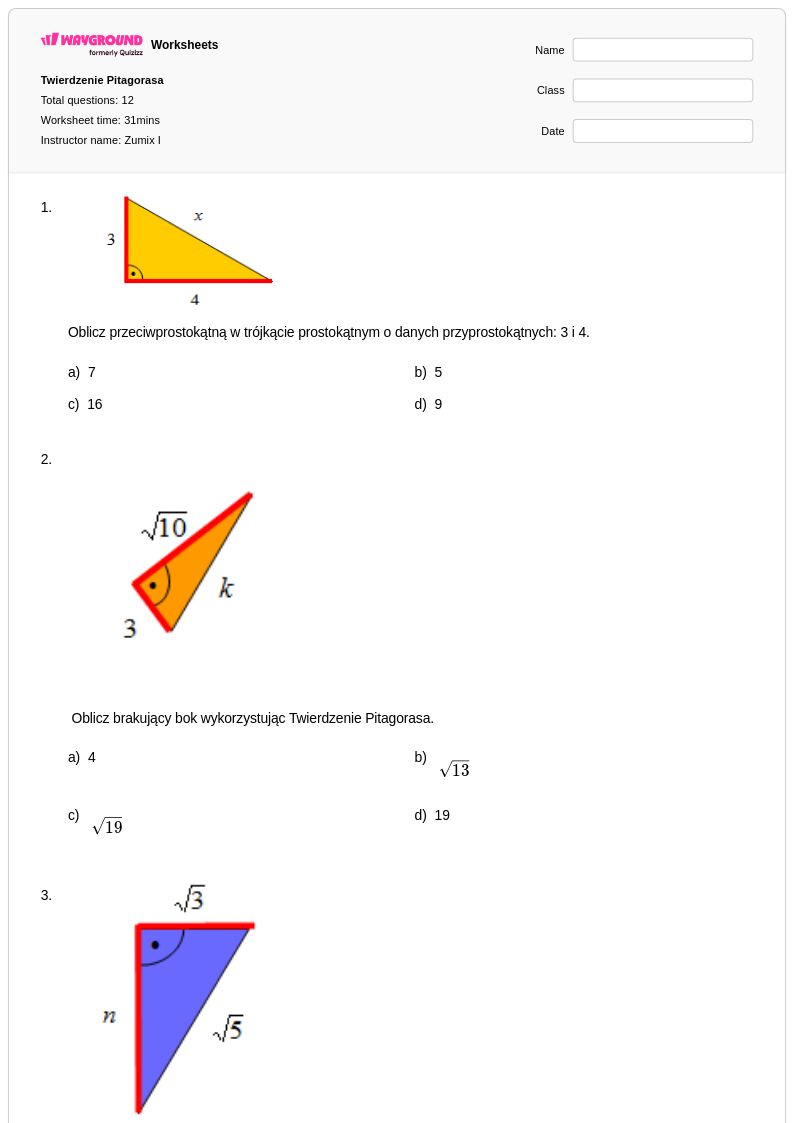
12 P
8th

93 P
8th
Przeglądaj arkusze według tematów
Przeglądaj arkusze robocze Twierdzenie o trójkącie równoramiennym do wydrukowania
Arkusze ćwiczeń z twierdzenia o trójkącie równoramiennym dostępne w Wayground (dawniej Quizizz) zapewniają uczniom wszechstronne możliwości praktycznego opanowania jednej z fundamentalnych zasad geometrii. Te starannie zaprojektowane zasoby pomagają uczniom zrozumieć, że kąty przy podstawie trójkąta równoramiennego są przystające, a jednocześnie rozwijają niezbędne umiejętności w zakresie pomiaru kątów, klasyfikacji trójkątów i konstruowania dowodów geometrycznych. Zbiór arkuszy ćwiczeń zawiera różnorodne zadania praktyczne, od podstawowej identyfikacji kątów po złożone, wieloetapowe dowody, a każdy materiał do druku zawiera szczegółowe klucze odpowiedzi, wspierające samodzielną naukę i samoocenę. Uczniowie pracują z bezpłatnymi, dostępnymi do pobrania ćwiczeniami, które wzmacniają zastosowanie twierdzenia w rzeczywistych kontekstach, budując pewność siebie w rozumowaniu geometrycznym, a jednocześnie wzmacniając umiejętność rozpoznawania i stosowania tej kluczowej zależności w różnych sytuacjach matematycznych.
Wayground (dawniej Quizizz) udostępnia nauczycielom miliony stworzonych przez nauczycieli zasobów dotyczących twierdzenia o trójkącie równoramiennym, które usprawniają planowanie lekcji i podnoszą jakość nauczania. Rozbudowane funkcje wyszukiwania i filtrowania platformy pozwalają nauczycielom szybko znaleźć arkusze ćwiczeń zgodne z określonymi standardami matematycznymi, a narzędzia różnicujące umożliwiają płynne dostosowanie do zróżnicowanych potrzeb edukacyjnych i poziomów umiejętności. Te obszerne zbiory są dostępne zarówno w formatach PDF do druku, jak i w interaktywnych wersjach cyfrowych, zapewniając elastyczność w nauczaniu w klasie, zadawaniu prac domowych i przygotowywaniu się do testów. Nauczyciele wykorzystują te wszechstronne zasoby do ukierunkowanego ćwiczenia umiejętności, wsparcia w nauce dla uczniów mających trudności oraz możliwości wzbogacenia wiedzy dla uczniów zaawansowanych, zapewniając każdemu uczniowi możliwość opanowania tej istotnej koncepcji geometrycznej poprzez odpowiednio wymagające i angażujące doświadczenia matematyczne.
