
13 Q
12th

21 Q
12th

10 Q
5th

12 Q
8th

12 Q
12th

11 Q
KG

20 Q
8th

10 Q
4th

12 Q
4th

16 Q
2nd

19 Q
8th

20 Q
7th
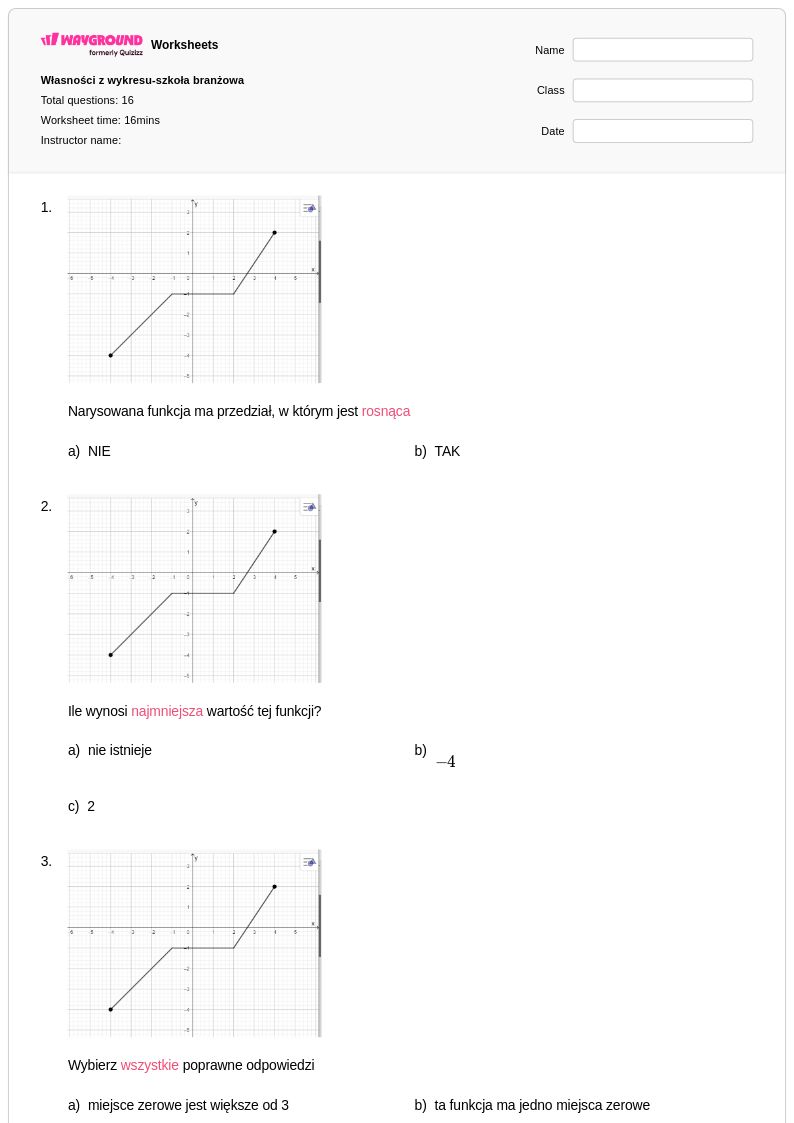
16 Q
10th
11 Q
5th

8 Q
3rd - 4th

33 Q
3rd - 5th

20 Q
6th

10 Q
7th - 8th

15 Q
6th - 8th

23 Q
12th

13 Q
6th - 8th

20 Q
12th

10 Q
1st
Explore Worksheets by Subjects
Przeglądaj arkusze robocze Dowody z równoległobokami do wydrukowania
Dowody z wykorzystaniem równoległoboków stanowią fundamentalny element rozumowania geometrycznego, wymagając od uczniów stosowania własności boków równoległych, przystających kątów przeciwległych i dwusiecznych przekątnych w celu konstruowania logicznych argumentów matematycznych. Obszerny zbiór arkuszy ćwiczeń Wayground koncentruje się na dowodach równoległoboków, oferując uczniom ustrukturyzowane zadania praktyczne, które rozwijają ich umiejętność identyfikowania podanych informacji, stosowania odpowiednich twierdzeń i konstruowania spójnych uzasadnień krok po kroku. Te bezpłatne, do druku materiały wzmacniają umiejętności krytycznego myślenia poprzez ćwiczenia obejmujące dowody geometrii współrzędnych, demonstracje w formacie dwukolumnowym i konstruowanie dowodów akapitowych. Każdy arkusz ćwiczeń zawiera szczegółowy klucz odpowiedzi, który pomaga uczniom zrozumieć prawidłowe rozumowanie matematyczne i konwencje notacji.
Solidna platforma Wayground zapewnia nauczycielom matematyki dostęp do milionów zasobów stworzonych przez nauczycieli, specjalnie zaprojektowanych do nauczania dowodzenia geometrycznego, oferując zaawansowane funkcje wyszukiwania i filtrowania, które umożliwiają szybką identyfikację materiałów dotyczących własności równoległoboków i technik dowodzenia. Zgodność platformy ze standardami gwarantuje, że zbiory arkuszy roboczych spełniają wymagania programowe, oferując jednocześnie narzędzia dywersyfikacyjne, dostosowane do różnych poziomów gotowości uczniów poprzez zmodyfikowaną złożoność problemów i zróżnicowane metody nauczania. Nauczyciele mogą dostosowywać te zasoby cyfrowe i PDF do konkretnych ćwiczeń umiejętności, wsparcia korekcyjnego dla uczniów mających trudności z logicznym rozumowaniem lub ćwiczeń wzbogacających dla uczniów zaawansowanych, gotowych do radzenia sobie ze złożonymi, wieloetapowymi dowodami, co sprawia, że planowanie lekcji jest bardziej efektywne i dostosowane do zróżnicowanych potrzeb klasy.
