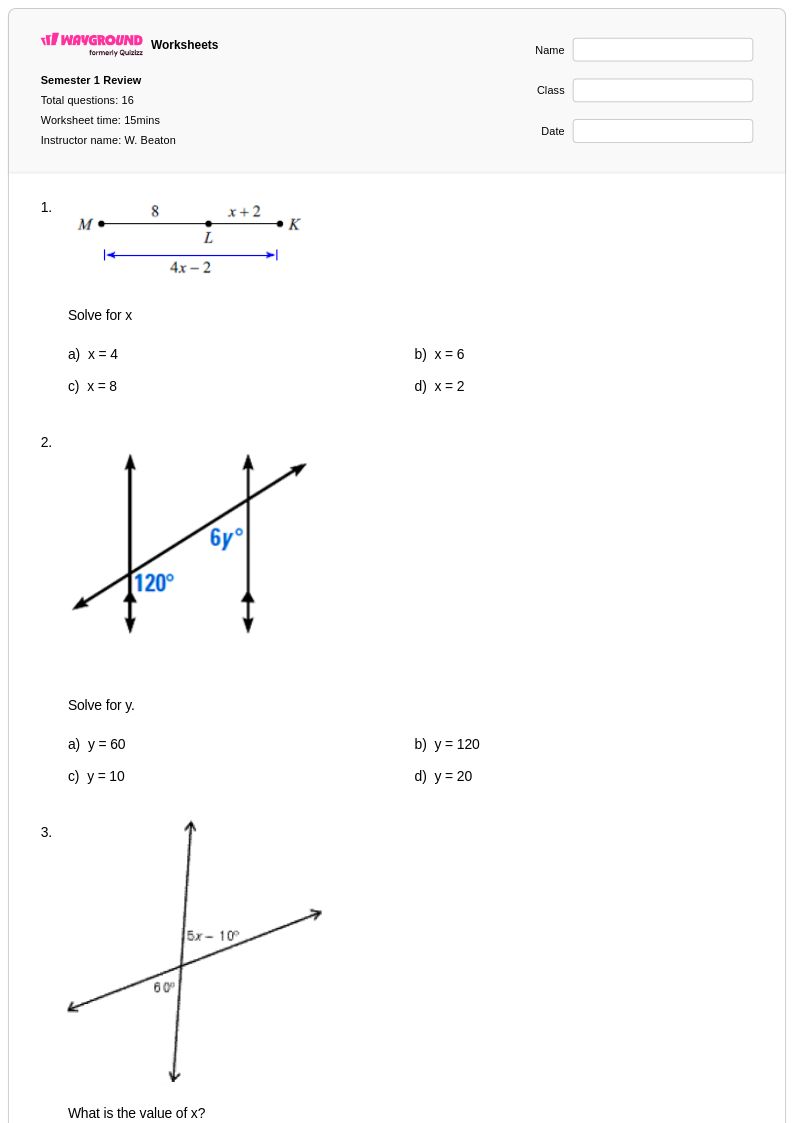
16 คิว
8th

24 คิว
7th - 11th

66 คิว
8th - 10th

243 คิว
8th
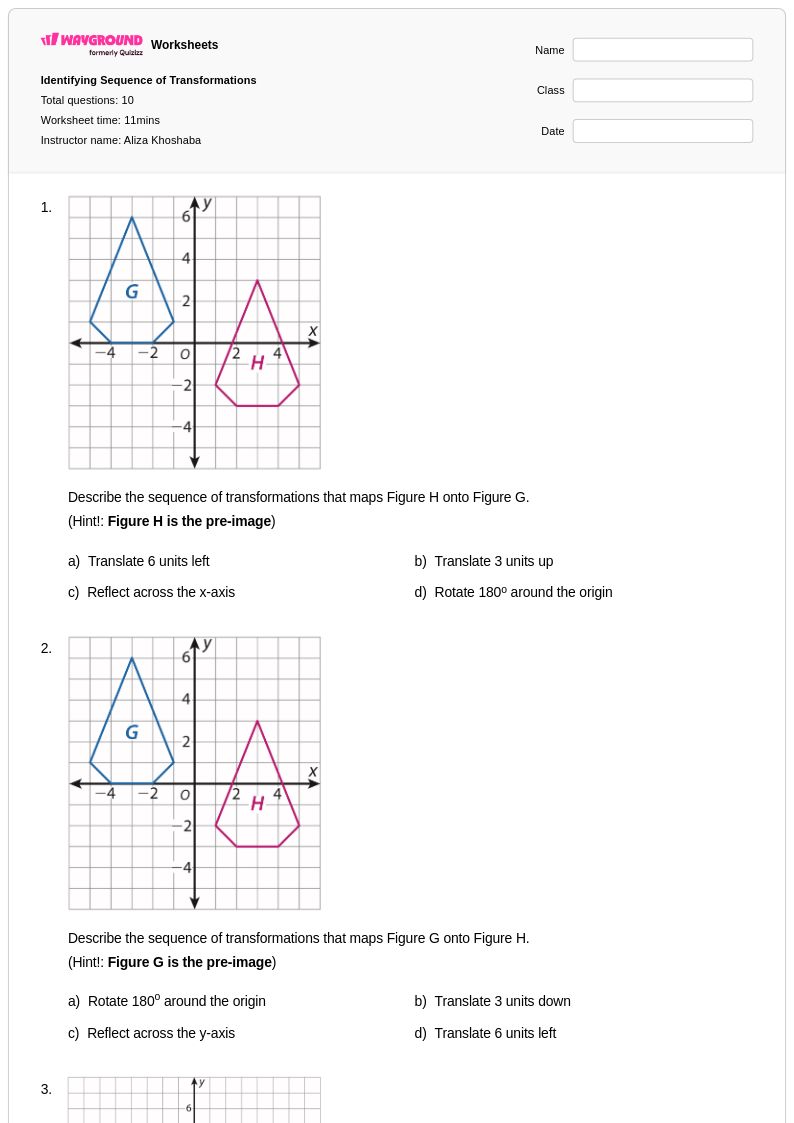
10 คิว
8th

13 คิว
8th

21 คิว
8th

16 คิว
7th - 12th

15 คิว
8th

30 คิว
8th - 10th

50 คิว
8th

20 คิว
8th

15 คิว
8th

11 คิว
8th - 12th
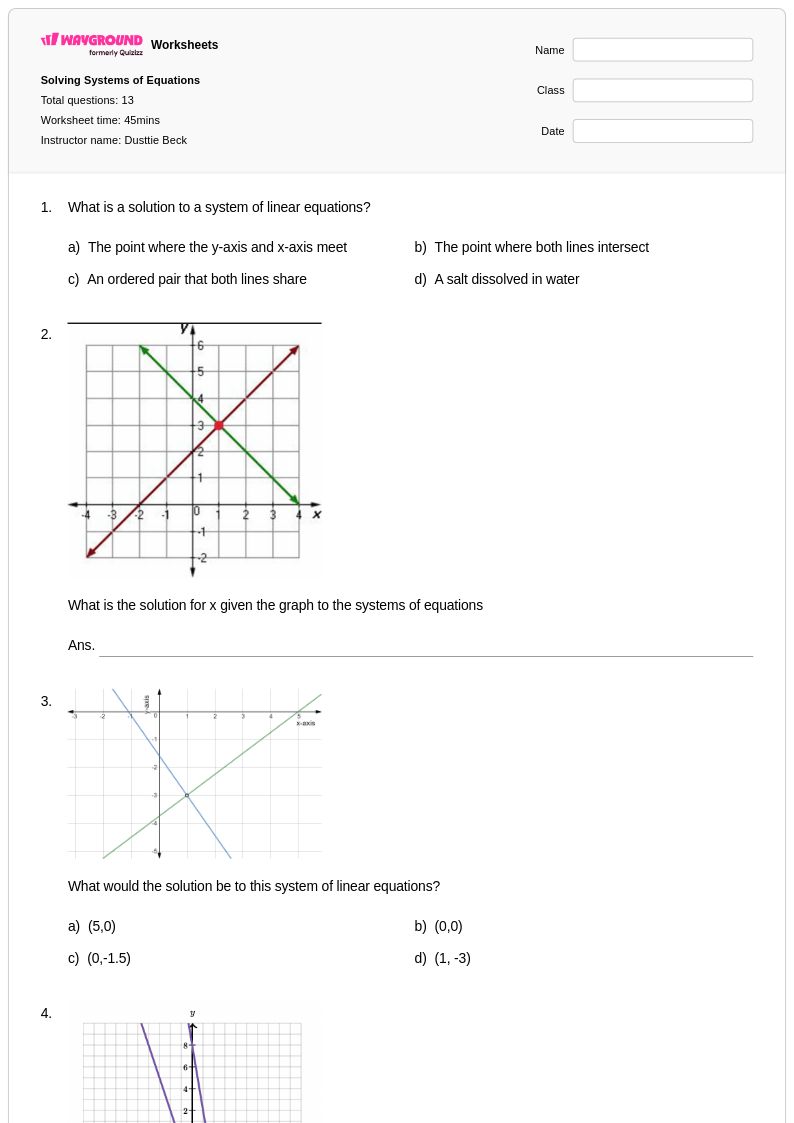
13 คิว
8th
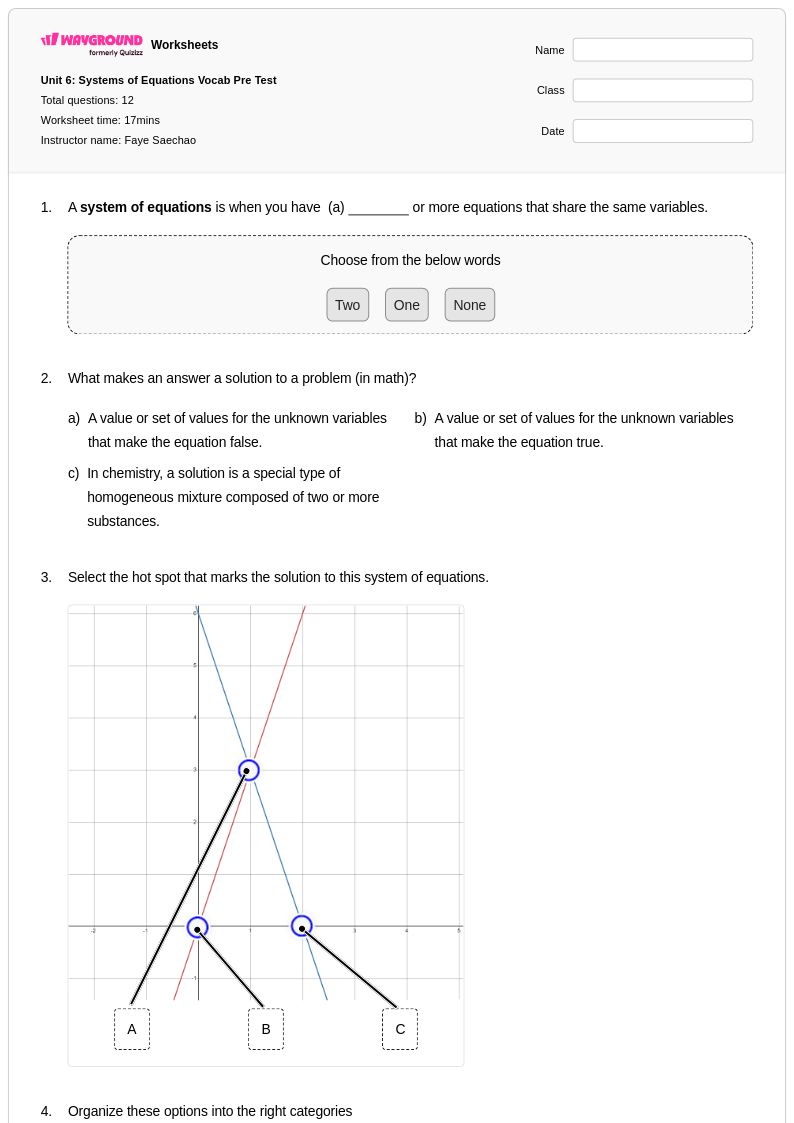
12 คิว
8th
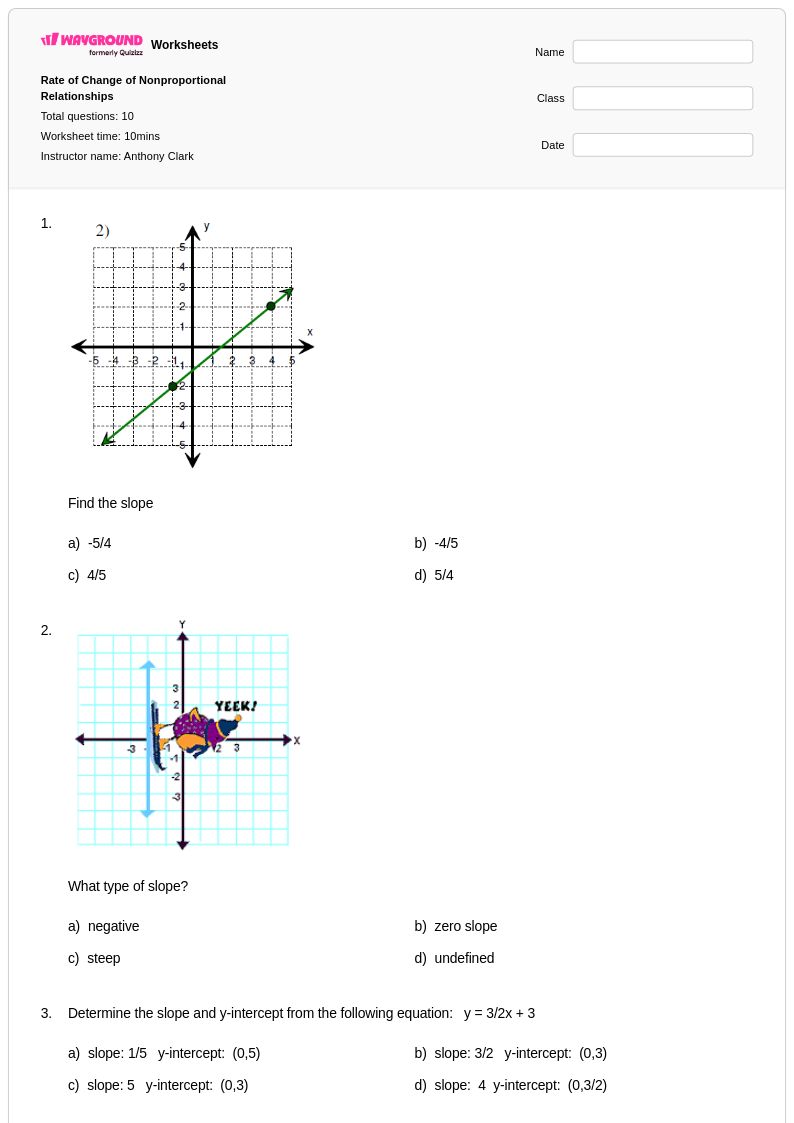
10 คิว
8th - Uni

25 คิว
8th - 12th

20 คิว
8th - Uni

12 คิว
8th - Uni
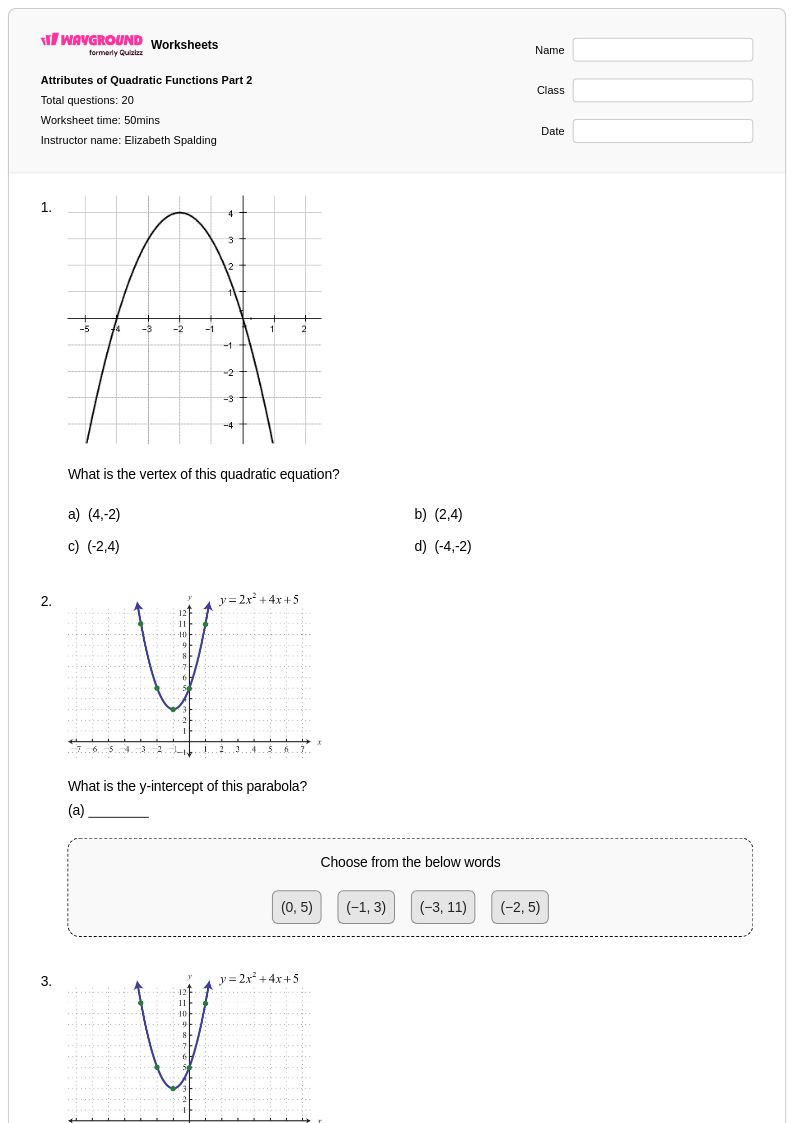
20 คิว
8th
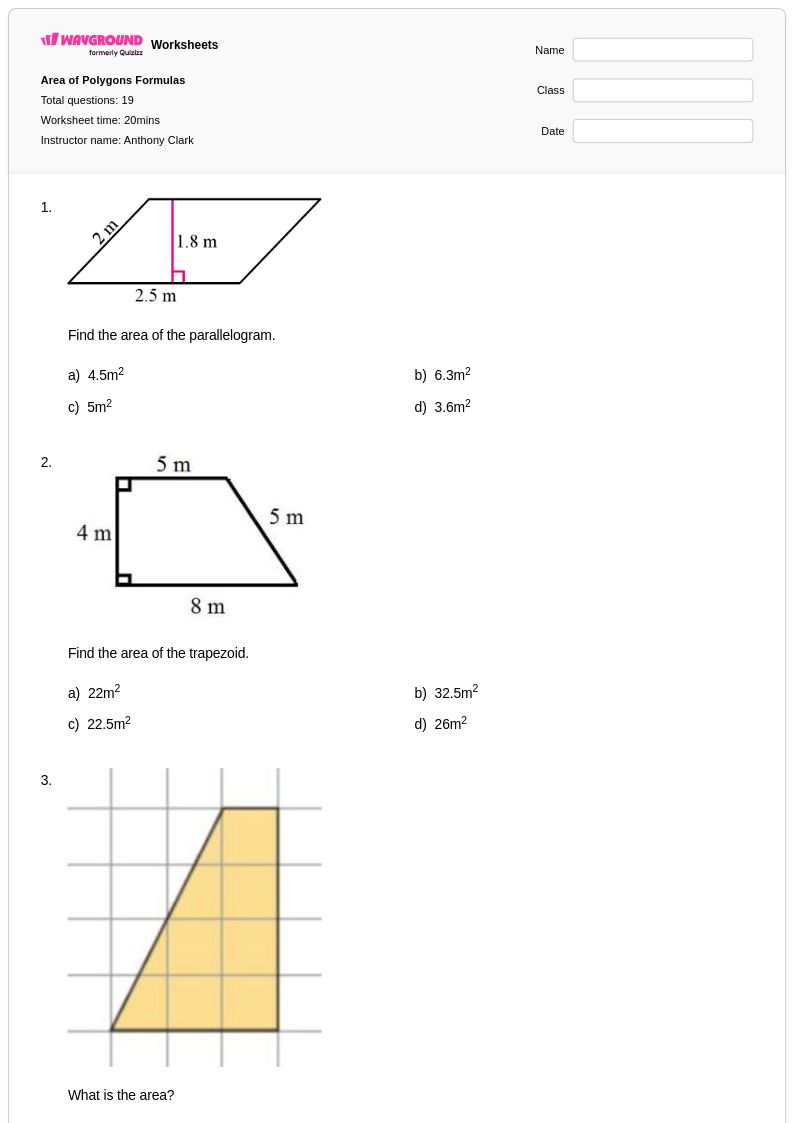
20 คิว
6th - Uni

29 คิว
8th - 10th
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 8
สำรวจแผ่นงาน กฎแห่งการไม่ยึดติด ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 8
แบบฝึกหัดกฎการแยกส่วน (Law of Detachment) สำหรับนักเรียนชั้น ม.2 จาก Wayground ให้การฝึกฝนอย่างครอบคลุมเกี่ยวกับหลักการพื้นฐานของการให้เหตุผลเชิงตรรกะในวิชาคณิตศาสตร์ แหล่งข้อมูลที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยให้นักเรียนเชี่ยวชาญทักษะการสรุปผลที่ถูกต้องจากประโยคเงื่อนไขและข้อสมมติที่กำหนดให้ เสริมสร้างความสามารถในการสร้างข้อโต้แย้งเชิงตรรกะและตระหนักถึงรูปแบบการให้เหตุผลแบบนิรนัยที่ถูกต้อง แบบฝึกหัดมีโจทย์ฝึกฝนหลากหลายรูปแบบที่ช่วยแนะนำนักเรียนในการระบุสมมติฐานและข้อสรุปในประโยคเงื่อนไข จากนั้นจึงนำกฎการแยกส่วนไปใช้เพื่อให้ได้ข้อสรุปเชิงตรรกะ แบบฝึกหัดแต่ละชุดมีเฉลยคำตอบโดยละเอียดที่ช่วยให้นักเรียนตรวจสอบกระบวนการให้เหตุผลของตนเองทีละขั้นตอน ในขณะที่รูปแบบไฟล์ PDF ที่พิมพ์ได้ฟรีทำให้แหล่งข้อมูลเหล่านี้เข้าถึงได้ง่ายสำหรับการใช้งานในห้องเรียน การบ้าน หรือการเรียนรู้ด้วยตนเอง
Wayground สนับสนุนครูผู้สอนคณิตศาสตร์ด้วยแหล่งข้อมูลกฎการแยกส่วนที่สร้างโดยครูหลายล้านรายการ ซึ่งสามารถค้นหาได้ง่ายผ่านความสามารถในการค้นหาและกรองข้อมูลที่มีประสิทธิภาพซึ่งออกแบบมาโดยเฉพาะสำหรับการสอนตรรกะและการให้เหตุผลในชั้น ม.2 แพลตฟอร์มนี้มีแบบฝึกหัดมากมายที่ช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานหลักสูตร และปรับการสอนให้เหมาะสมกับความต้องการของนักเรียนแต่ละคน ไม่ว่าจะเป็นการแก้ไขปัญหาสำหรับนักเรียนที่เรียนอ่อน หรือกิจกรรมเสริมสำหรับนักเรียนที่เรียนเก่ง ครูสามารถปรับแต่งแบบฝึกหัดที่มีอยู่ หรือสร้างแบบฝึกหัดใหม่ให้ตรงกับวัตถุประสงค์ของบทเรียนได้ โดยมีตัวเลือกที่ยืดหยุ่นทั้งสำหรับการบูรณาการในห้องเรียนดิจิทัลและรูปแบบ PDF ที่พิมพ์ได้แบบดั้งเดิม เครื่องมือที่ครอบคลุมเหล่านี้ช่วยให้การวางแผนบทเรียนง่ายขึ้น ในขณะเดียวกันก็มอบการฝึกฝนทักษะที่ตรงเป้าหมาย ซึ่งช่วยให้นักเรียนพัฒนาความสามารถในการคิดเชิงวิเคราะห์และความเชี่ยวชาญด้านการให้เหตุผลทางคณิตศาสตร์ผ่านการเรียนรู้โครงสร้างการโต้แย้งเชิงตรรกะอย่างเป็นระบบ
