10 คิว
3rd - 12th

11 คิว
3rd - 4th
14 คิว
3rd
25 คิว
3rd

20 คิว
3rd

11 คิว
3rd - 4th

11 คิว
3rd - 4th
17 คิว
2nd - 11th

11 คิว
3rd - 4th

13 คิว
3rd - 5th

8 คิว
3rd - 5th
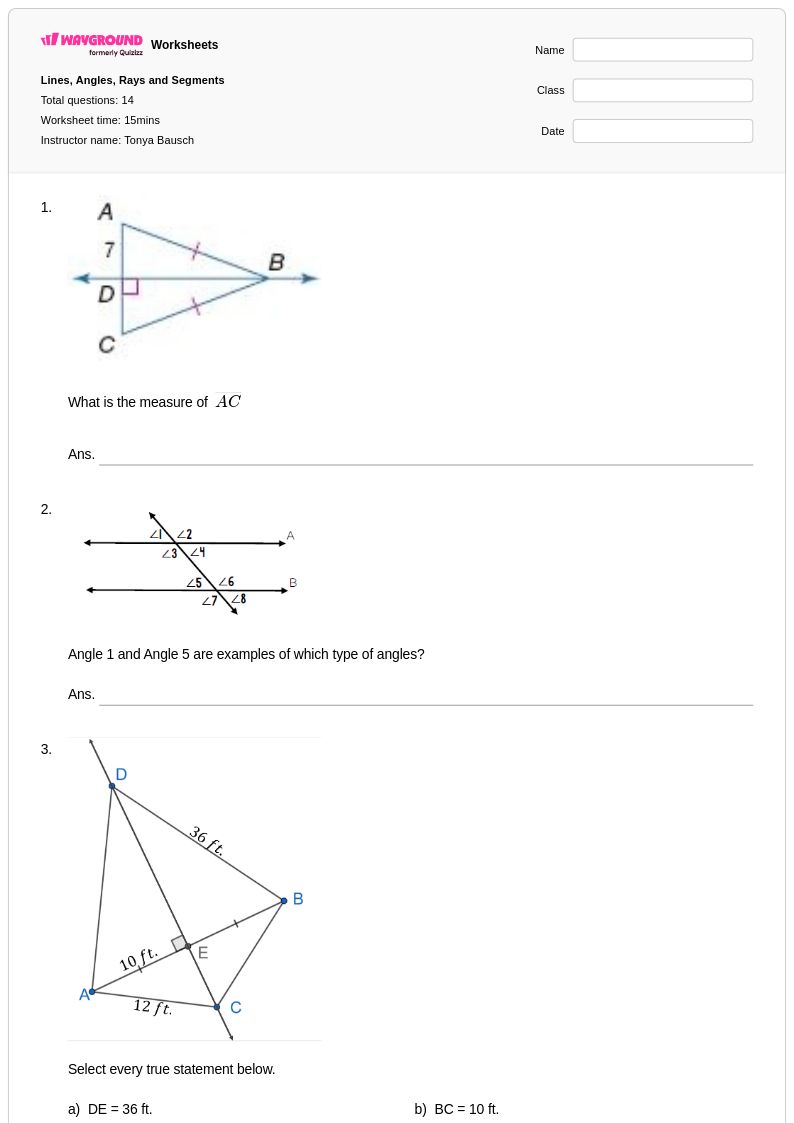
14 คิว
3rd
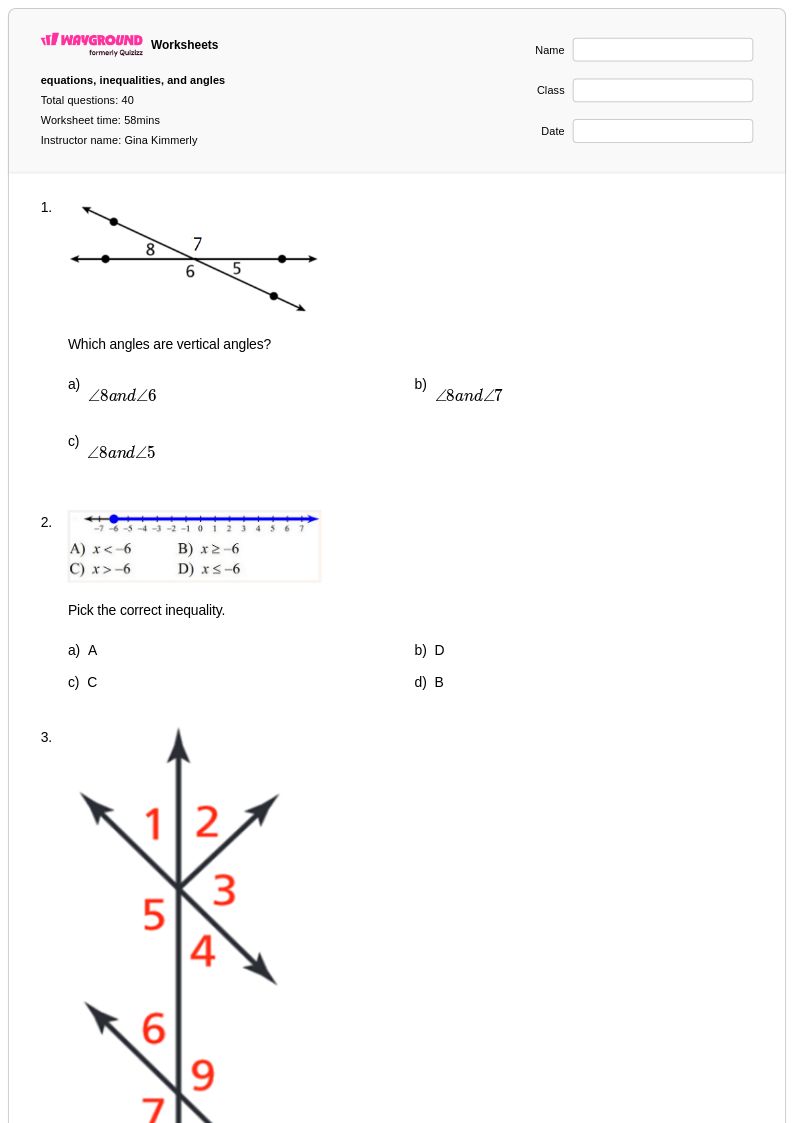
40 คิว
1st - 5th
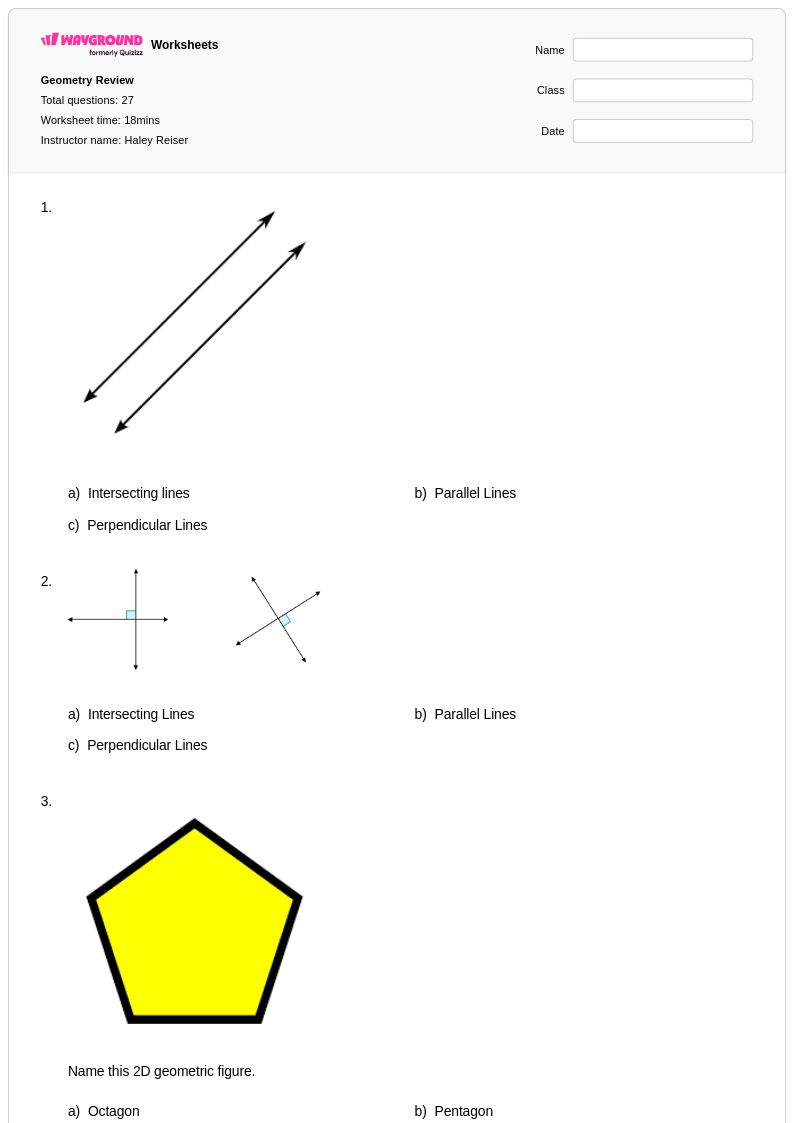
27 คิว
3rd
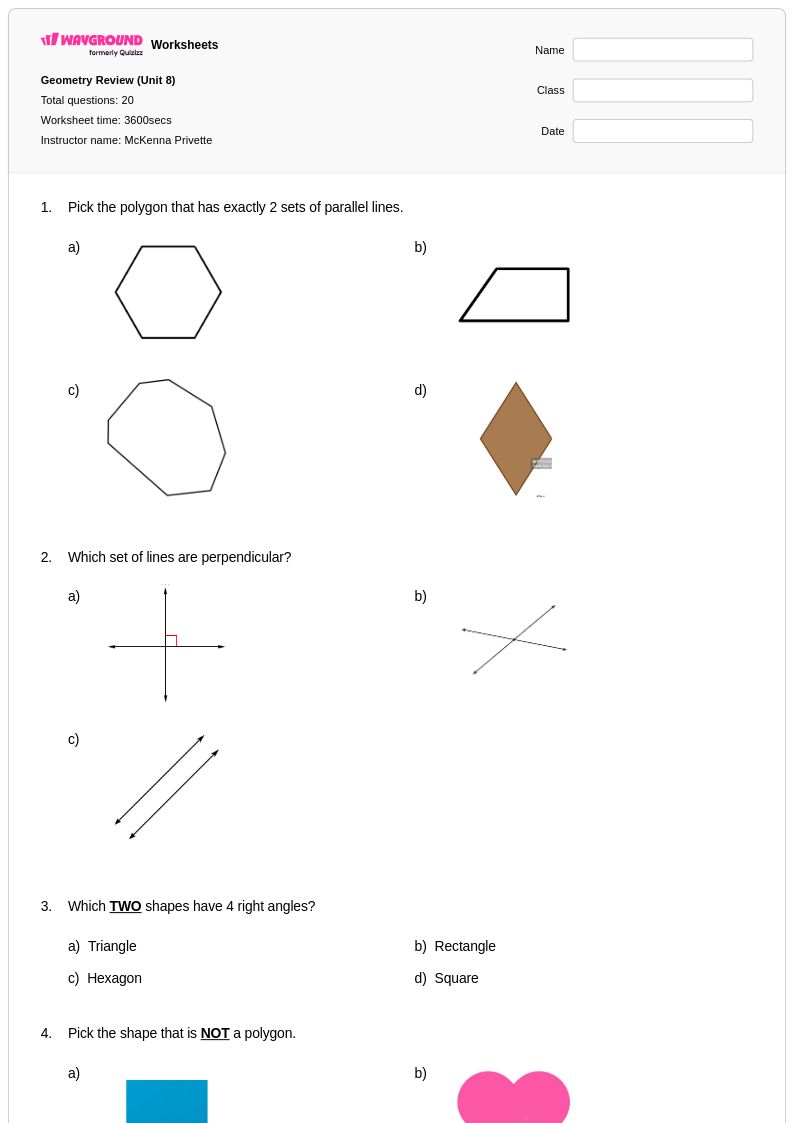
20 คิว
3rd
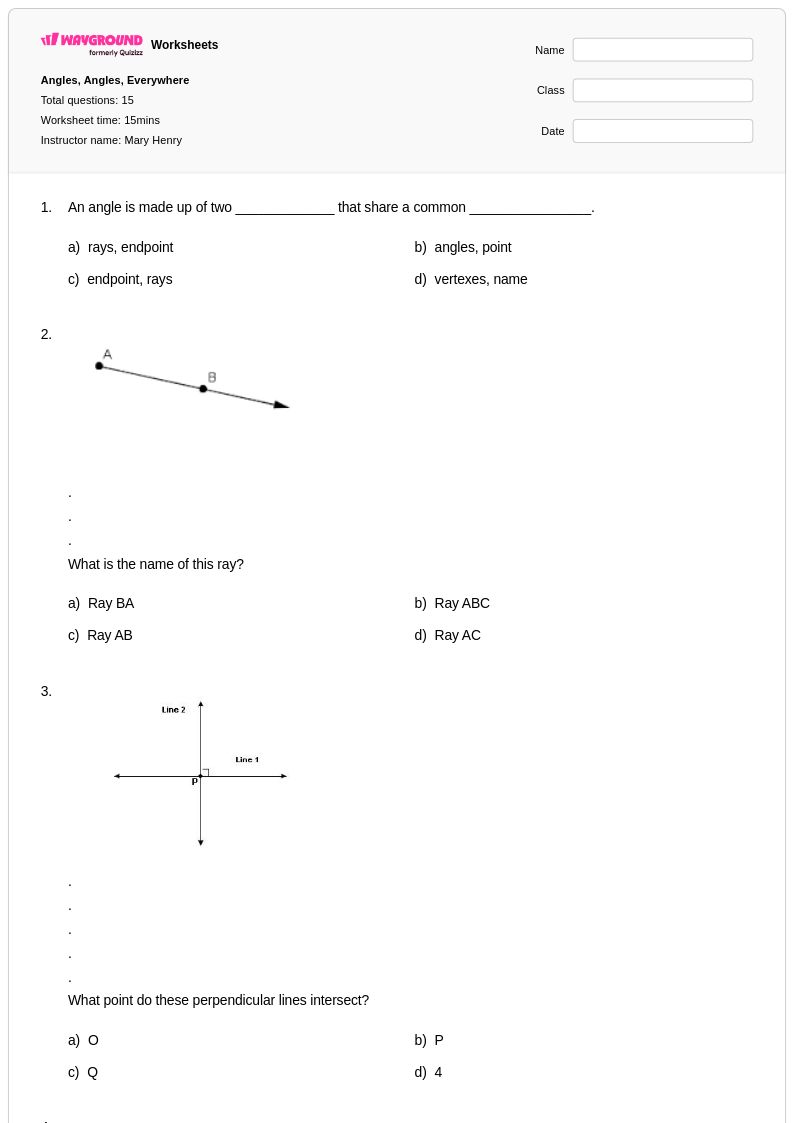
15 คิว
3rd - 4th
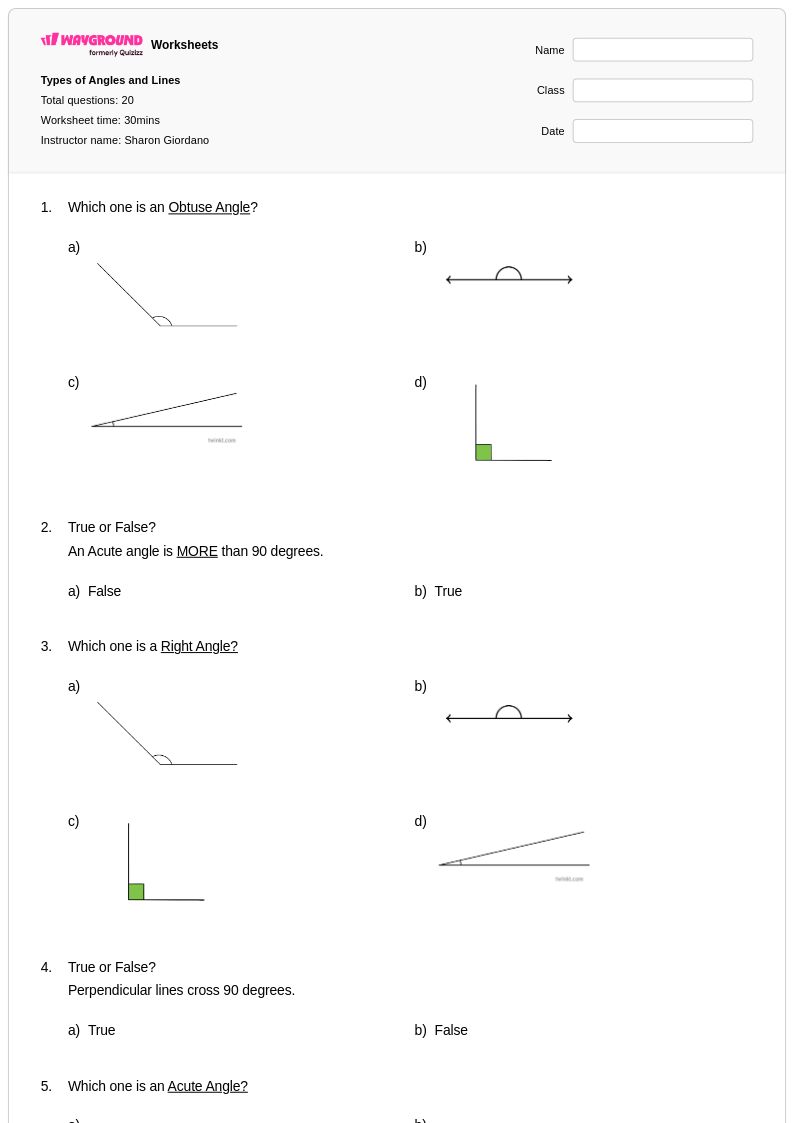
20 คิว
3rd
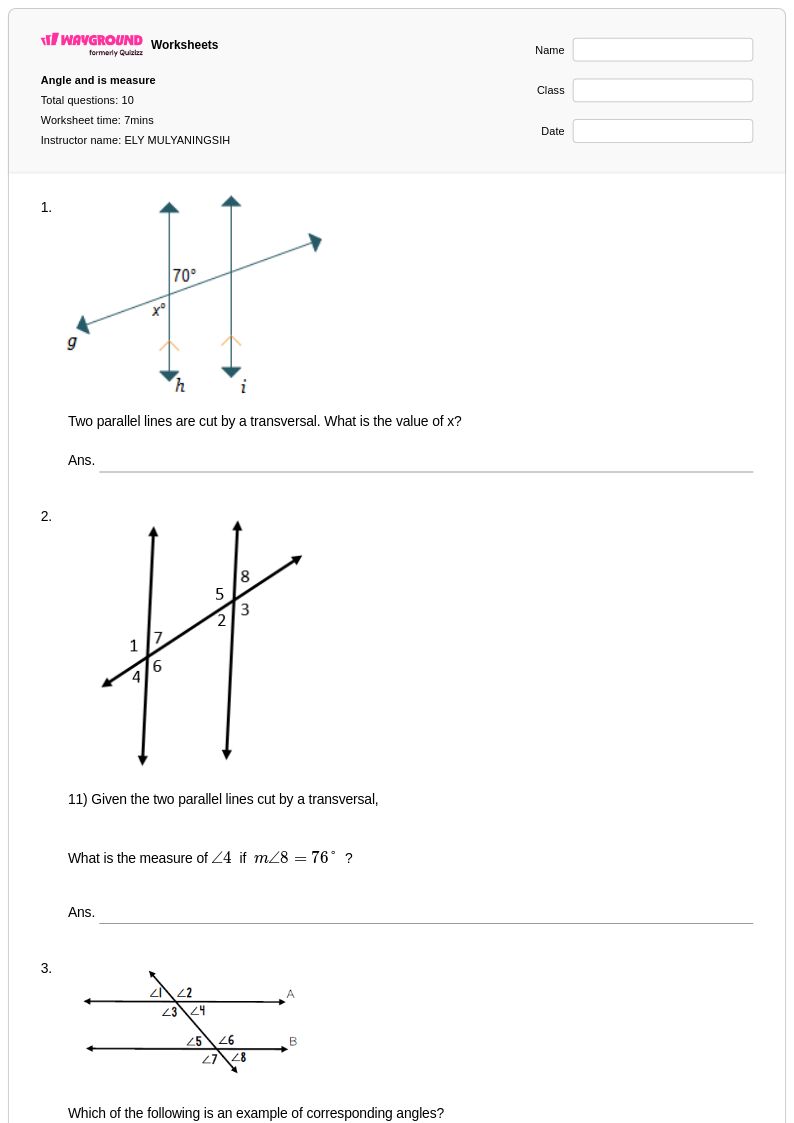
10 คิว
1st - 5th

20 คิว
1st - 5th

11 คิว
3rd - 4th

11 คิว
3rd - 4th
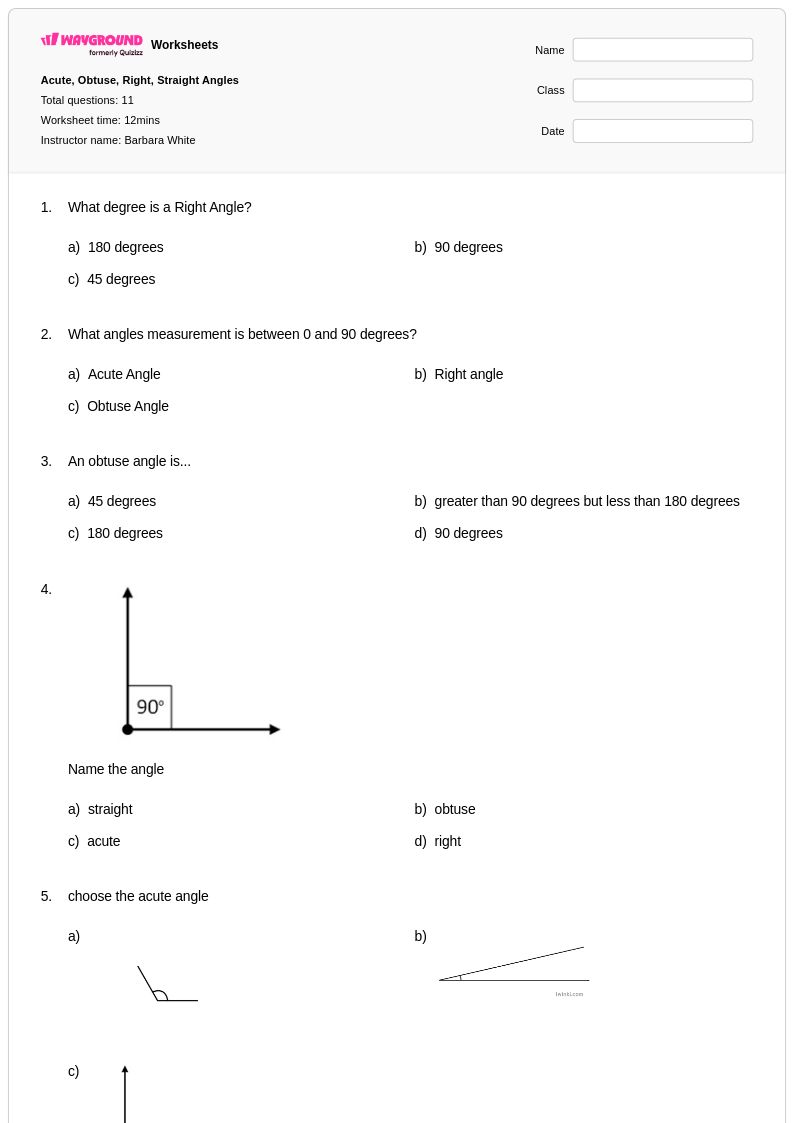
11 คิว
3rd - 4th

20 คิว
3rd - Uni
20 คิว
3rd
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 3
สำรวจแผ่นงาน การระบุมุม ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 3
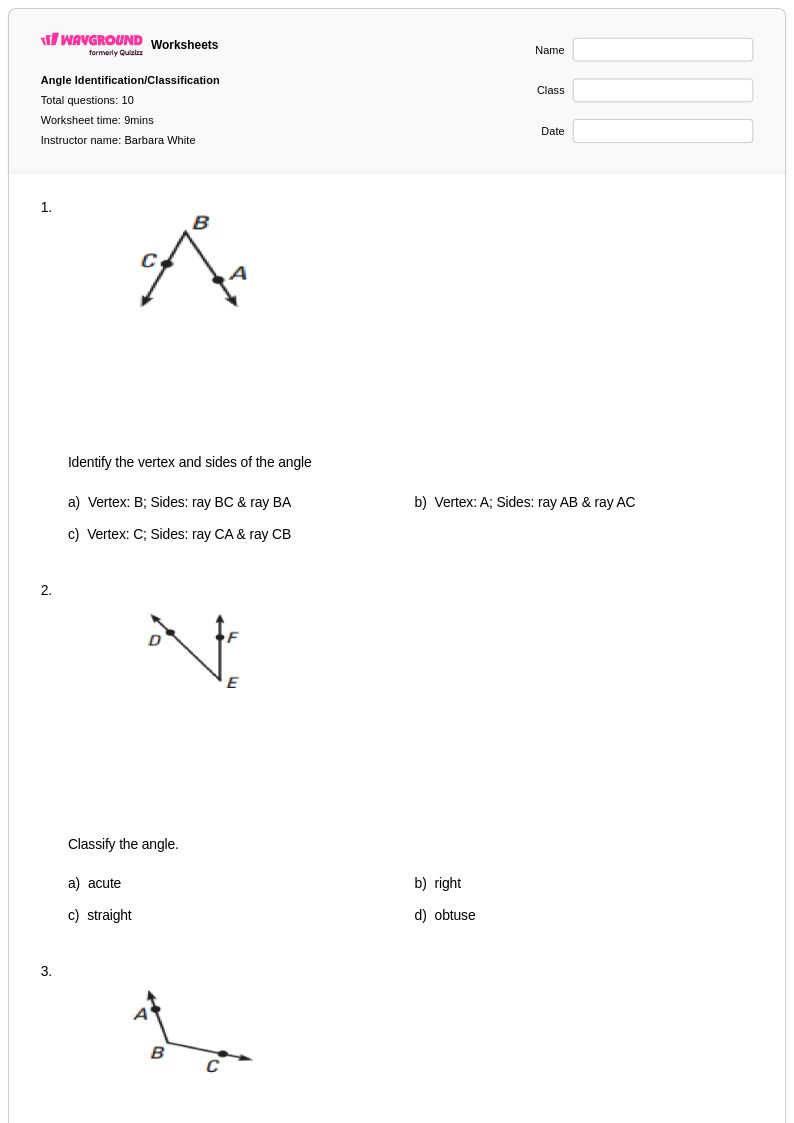
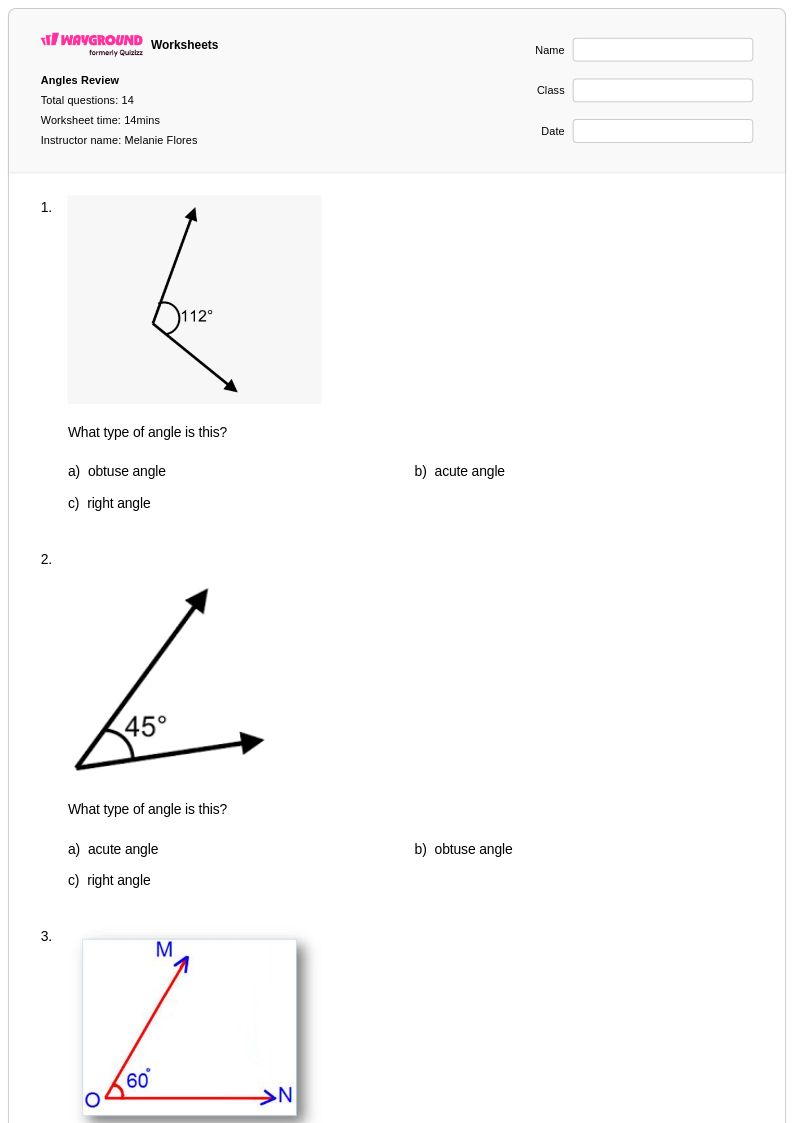
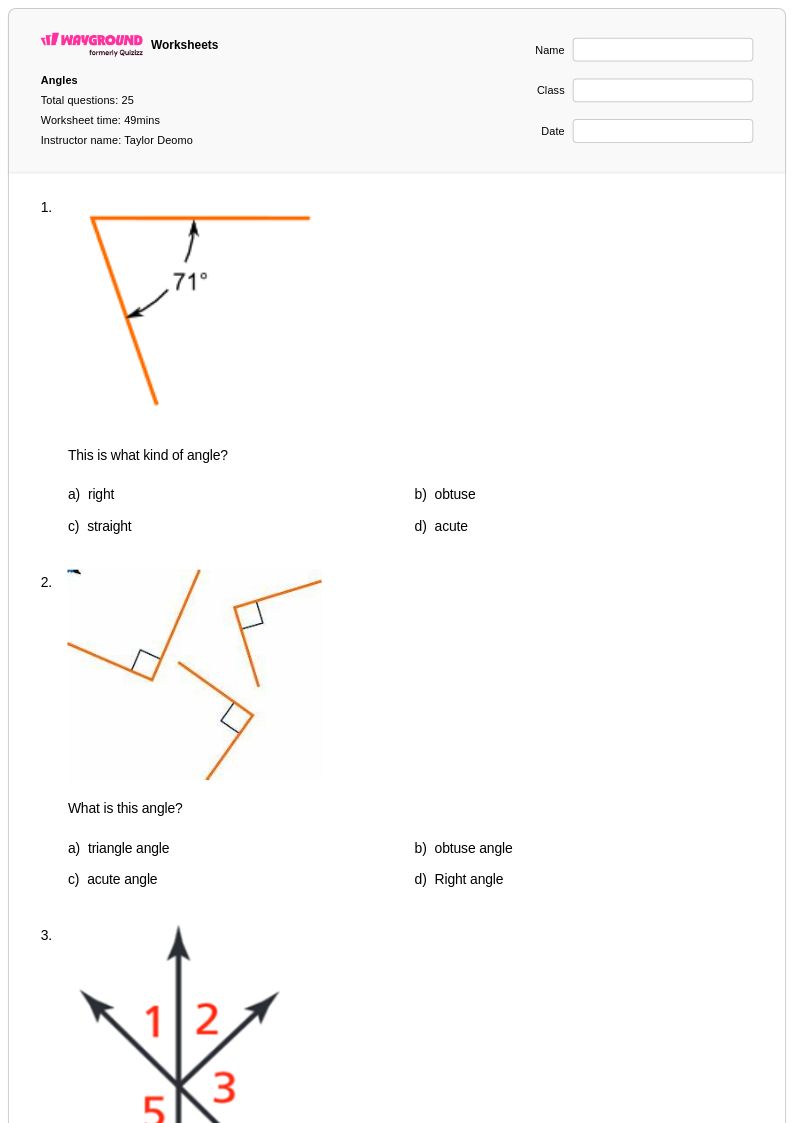
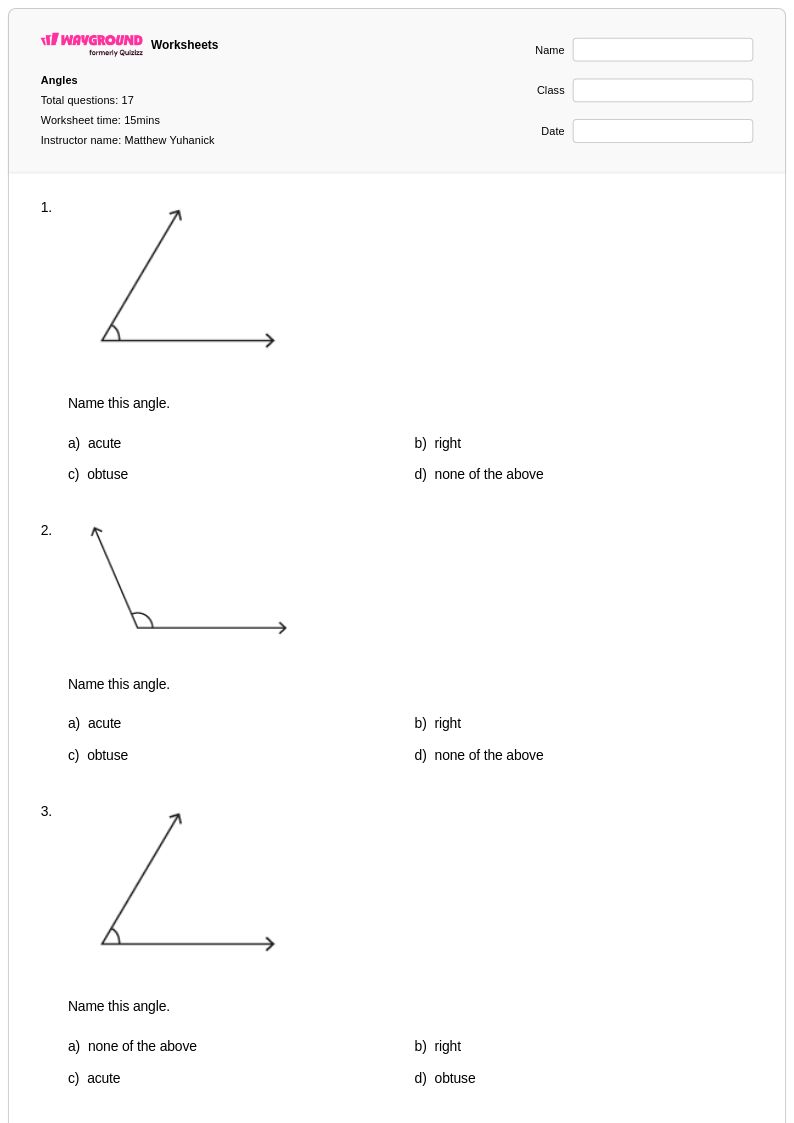
แบบฝึกหัดการระบุมุมสำหรับนักเรียนชั้นประถมศึกษาปีที่ 3 จาก Wayground (เดิมชื่อ Quizizz) เป็นแบบฝึกหัดเรขาคณิตพื้นฐานที่สำคัญ ช่วยพัฒนาการคิดเชิงพื้นที่และคำศัพท์ทางคณิตศาสตร์ แบบฝึกหัดเหล่านี้ได้รับการออกแบบอย่างพิถีพิถันเพื่อแนะนำผู้เรียนรุ่นเยาว์ให้รู้จักและแยกแยะความแตกต่างระหว่างมุมฉาก มุมแหลม และมุมป้าน โดยใช้ตัวอย่างภาพประกอบ วัตถุในชีวิตจริง และรูปทรงเรขาคณิต แบบฝึกหัดแต่ละแผ่นประกอบด้วยโจทย์ฝึกฝนที่ครอบคลุม ซึ่งช่วยสร้างความเข้าใจอย่างค่อยเป็นค่อยไป ตั้งแต่การระบุมุมในภาพวาดอย่างง่าย ไปจนถึงการหามุมในรูปทรงที่ซับซ้อนมากขึ้น และสิ่งของในชีวิตประจำวัน เช่น เข็มนาฬิกา มุมอาคาร และอุปกรณ์ในสนามเด็กเล่น เฉลยคำตอบที่แนบมาช่วยให้สามารถตรวจสอบและแก้ไขข้อผิดพลาดได้ทันที ในขณะที่รูปแบบไฟล์ PDF ฟรีช่วยให้เข้าถึงได้ง่ายทั้งในการเรียนการสอนในห้องเรียนและการฝึกฝนที่บ้าน
Wayground (เดิมชื่อ Quizizz) ช่วยเสริมศักยภาพให้ครูผู้สอนด้วยชุดทรัพยากรการระบุมุมที่สร้างโดยครูผู้สอนนับล้านรายการ ซึ่งสอดคล้องกับมาตรฐานคณิตศาสตร์ชั้นประถมศึกษาปีที่ 3 โดยเฉพาะ แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่ตรงกับความต้องการในการสอนได้อย่างรวดเร็ว ไม่ว่าจะเป็นการแนะนำทักษะเบื้องต้น การแก้ไขปัญหาเฉพาะจุด หรือกิจกรรมเสริมสำหรับผู้เรียนที่มีความสามารถสูง เครื่องมือปรับแต่งที่ยืดหยุ่นช่วยให้ครูสามารถแก้ไขแบบฝึกหัดที่มีอยู่ หรือสร้างแบบฝึกหัดที่แตกต่างกันเพื่อรองรับรูปแบบการเรียนรู้และระดับความสามารถที่หลากหลายในห้องเรียน แบบฝึกหัดเหล่านี้มีให้เลือกทั้งแบบพิมพ์ได้และแบบดิจิทัล สามารถบูรณาการเข้ากับขั้นตอนการวางแผนการสอนได้อย่างราบรื่น สนับสนุนทุกอย่างตั้งแต่การสอนทั้งชั้นเรียนไปจนถึงการฝึกฝนของนักเรียนแต่ละคน การบ้าน และการเตรียมการประเมินผล ในขณะเดียวกันก็รับประกันการพัฒนาทักษะอย่างสม่ำเสมอในแนวคิดทางเรขาคณิตที่สำคัญนี้
