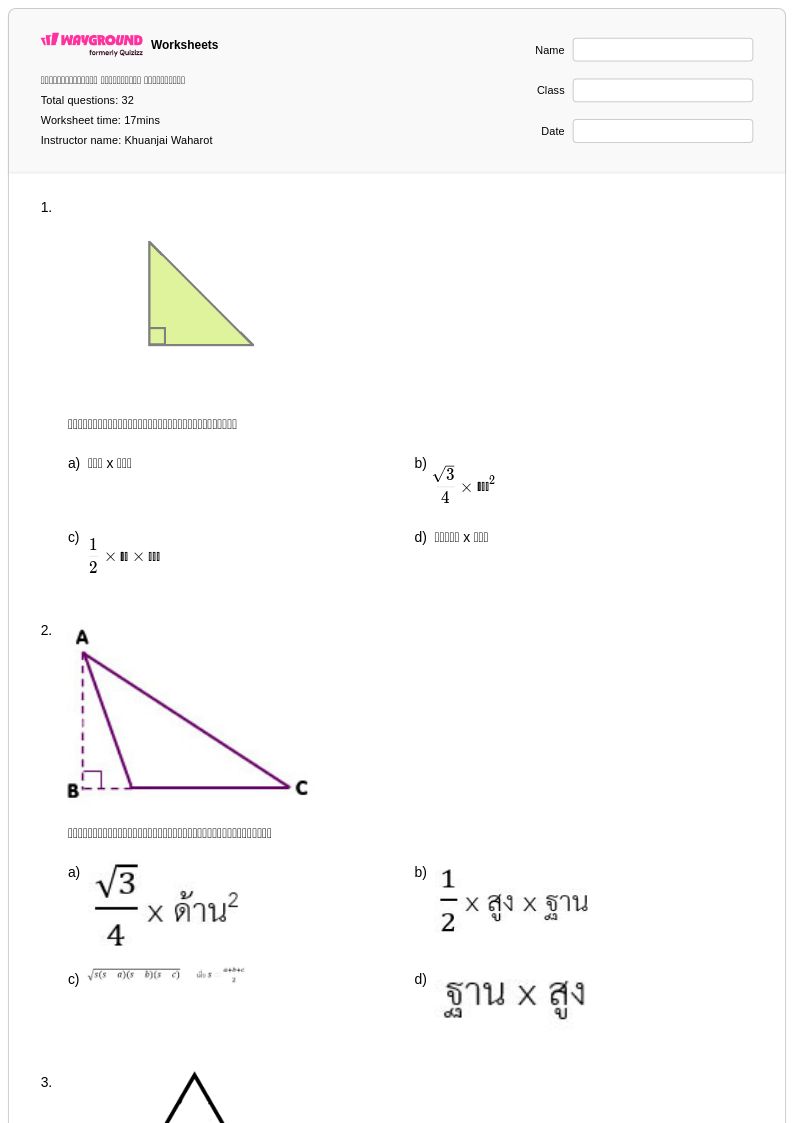
32 P
6th - 8th
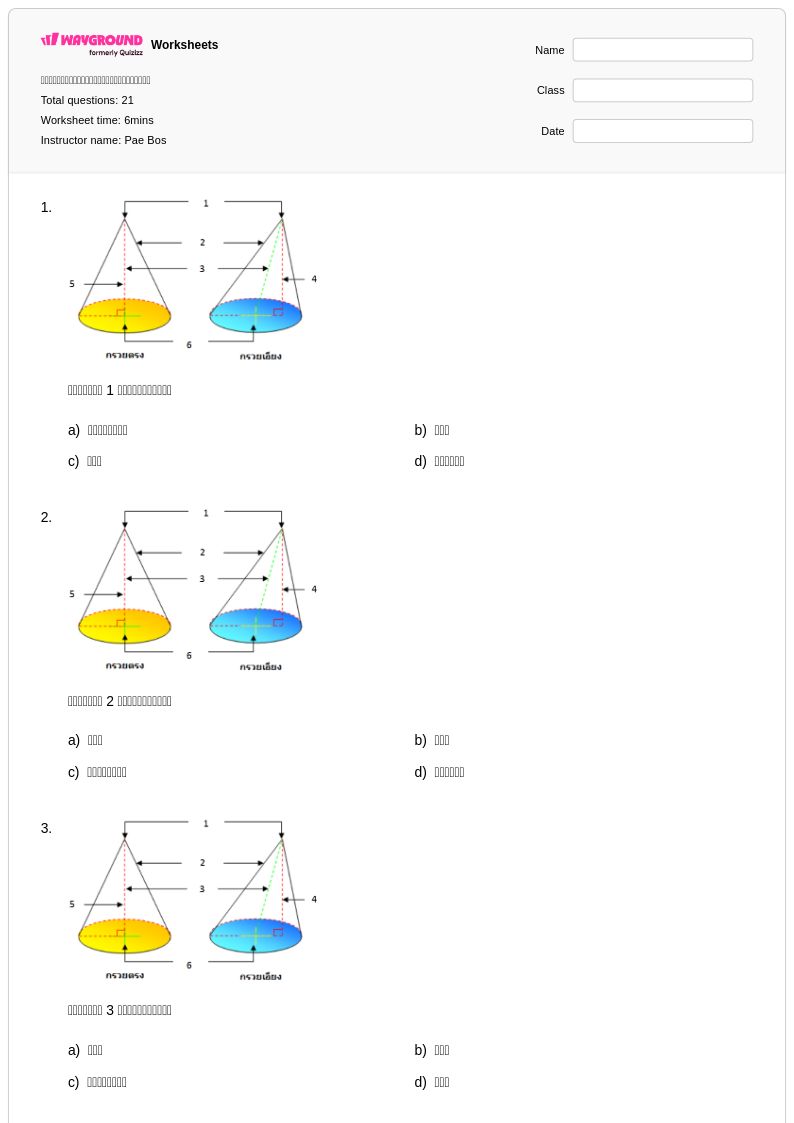
21 P
6th - 8th
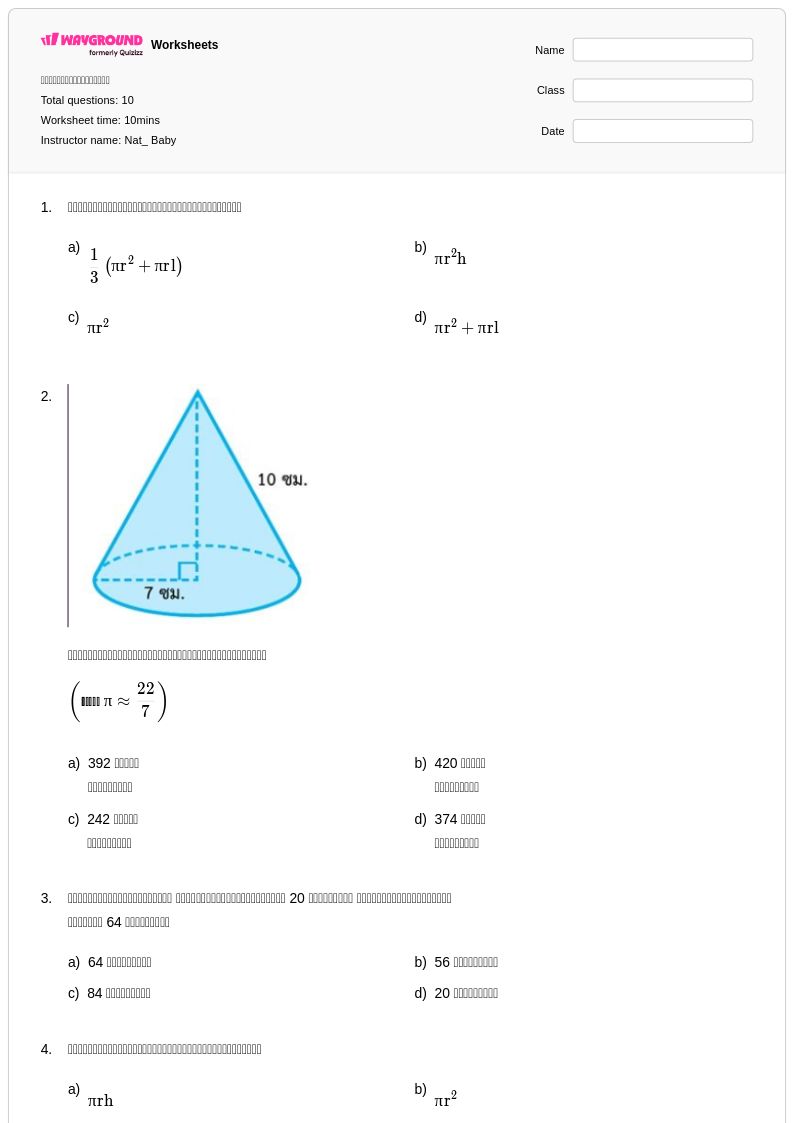
10 P
6th - 8th
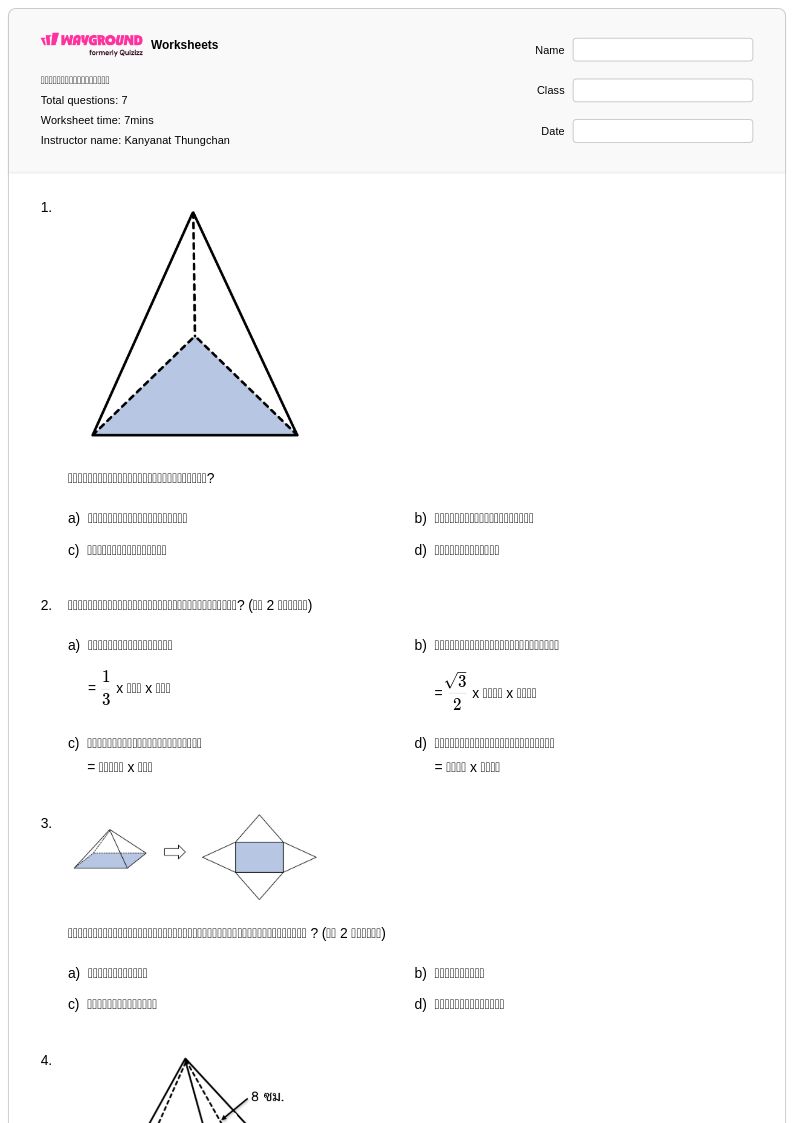
7 P
6th - 8th
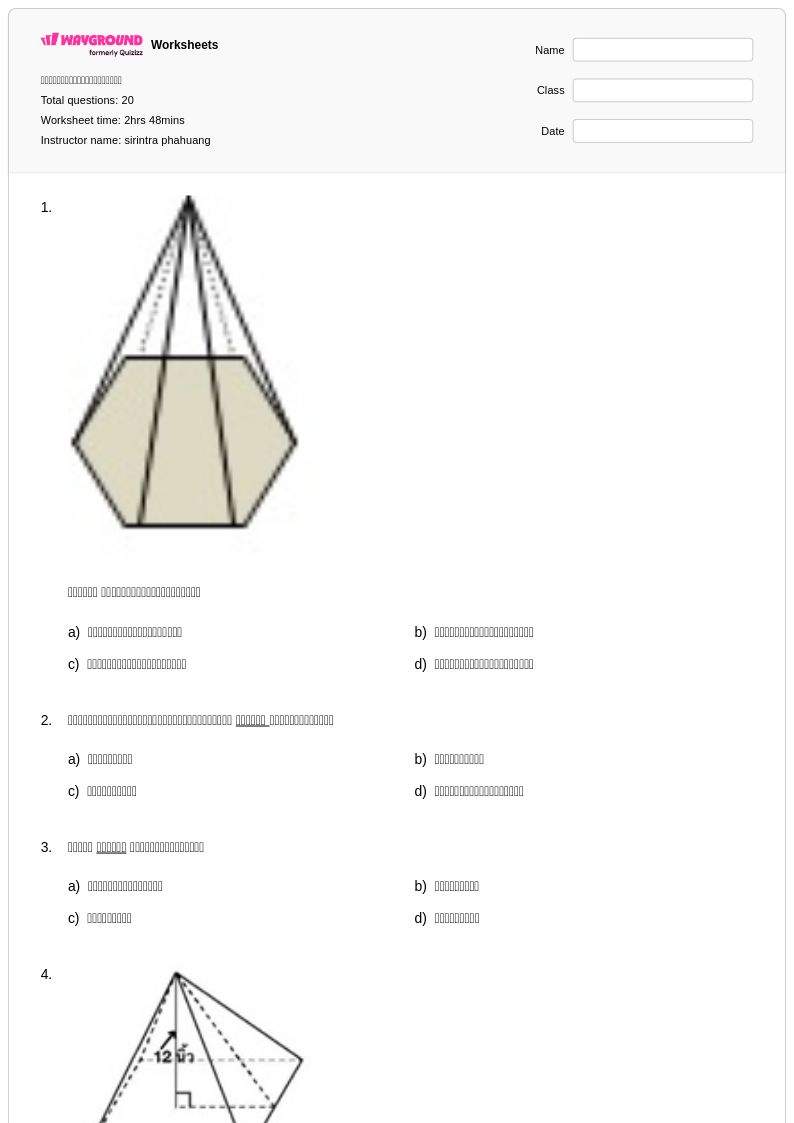
20 P
6th
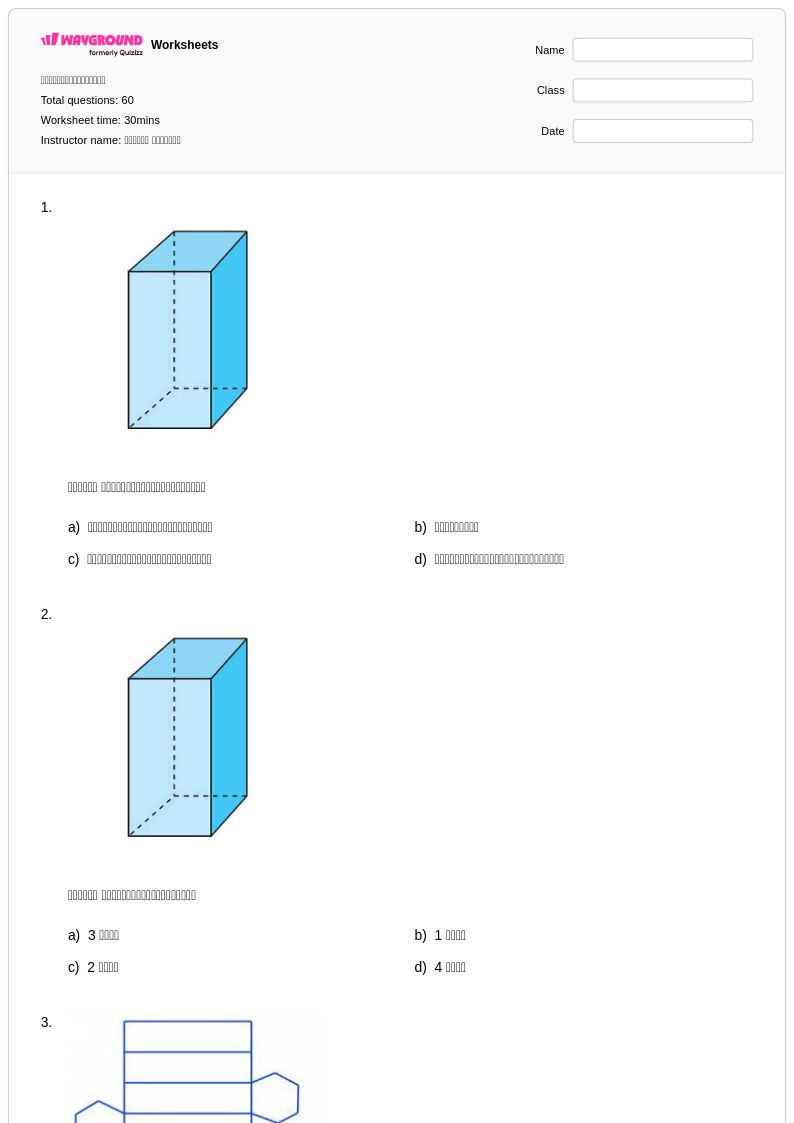
60 P
6th - 12th

10 P
1st - 12th
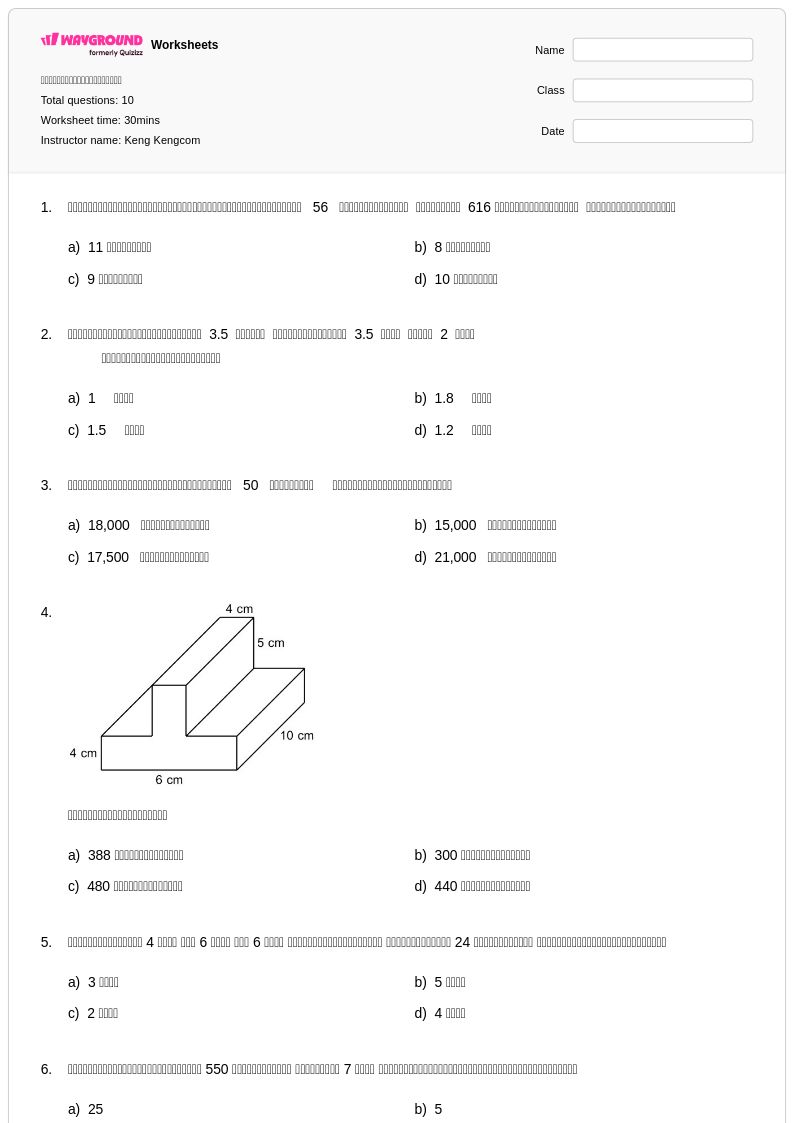
10 P
1st - 12th

7 P
6th - 8th
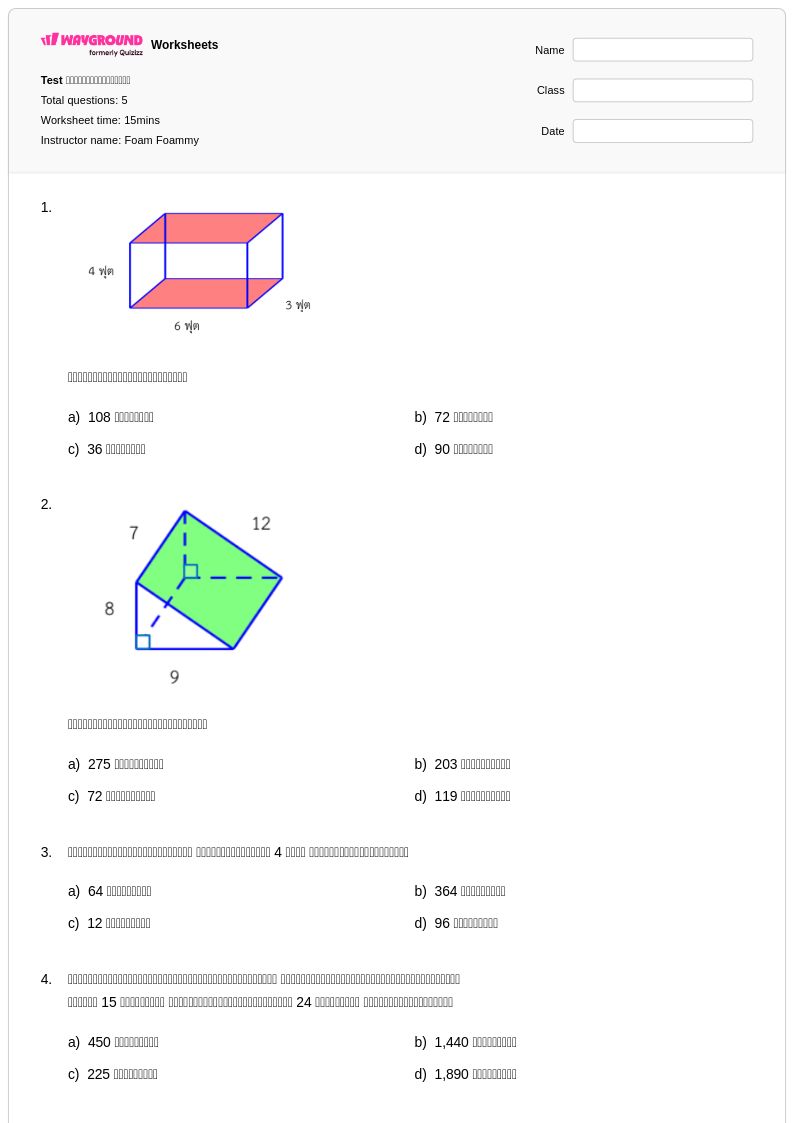
5 P
6th - 8th
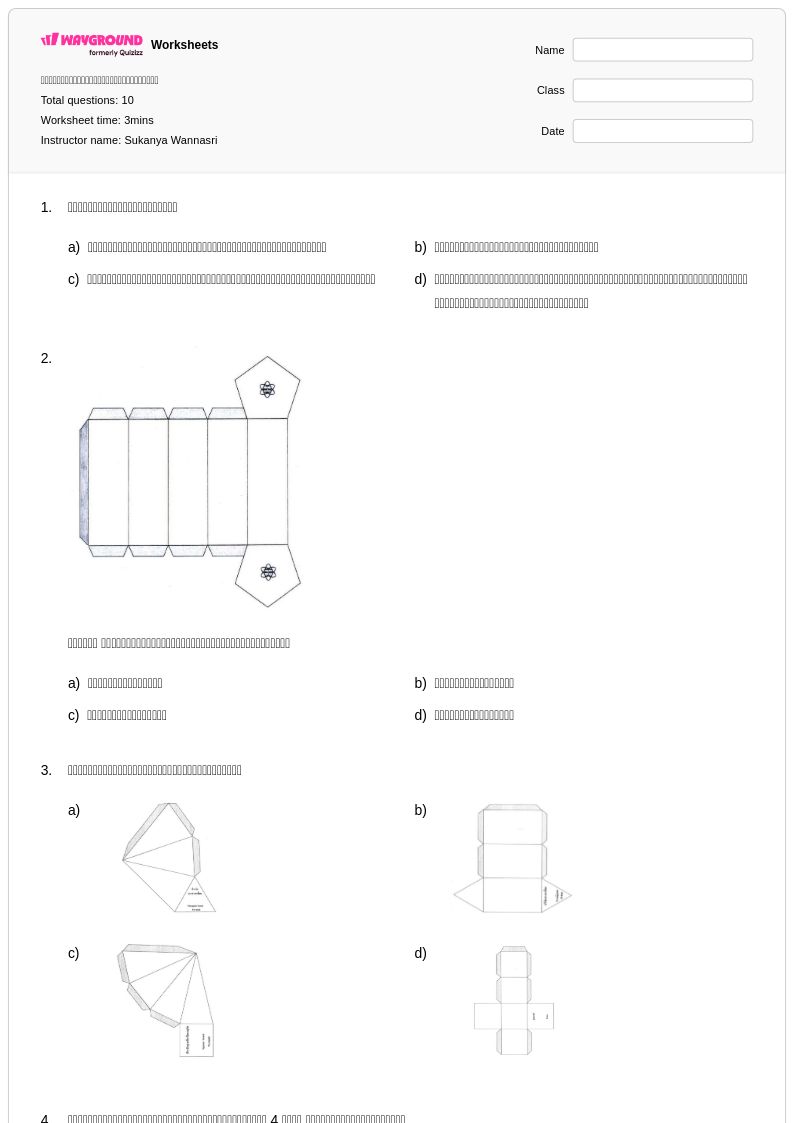
10 P
6th - 8th

10 P
6th - 8th
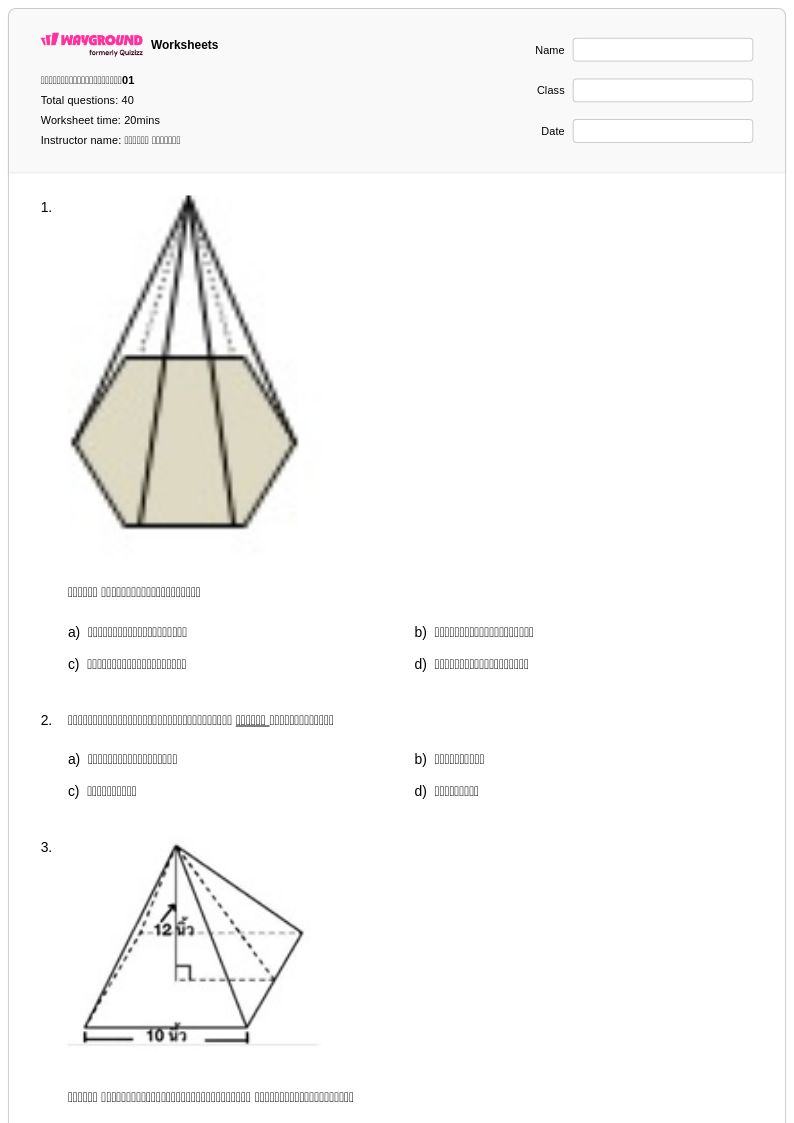
40 P
4th - 8th
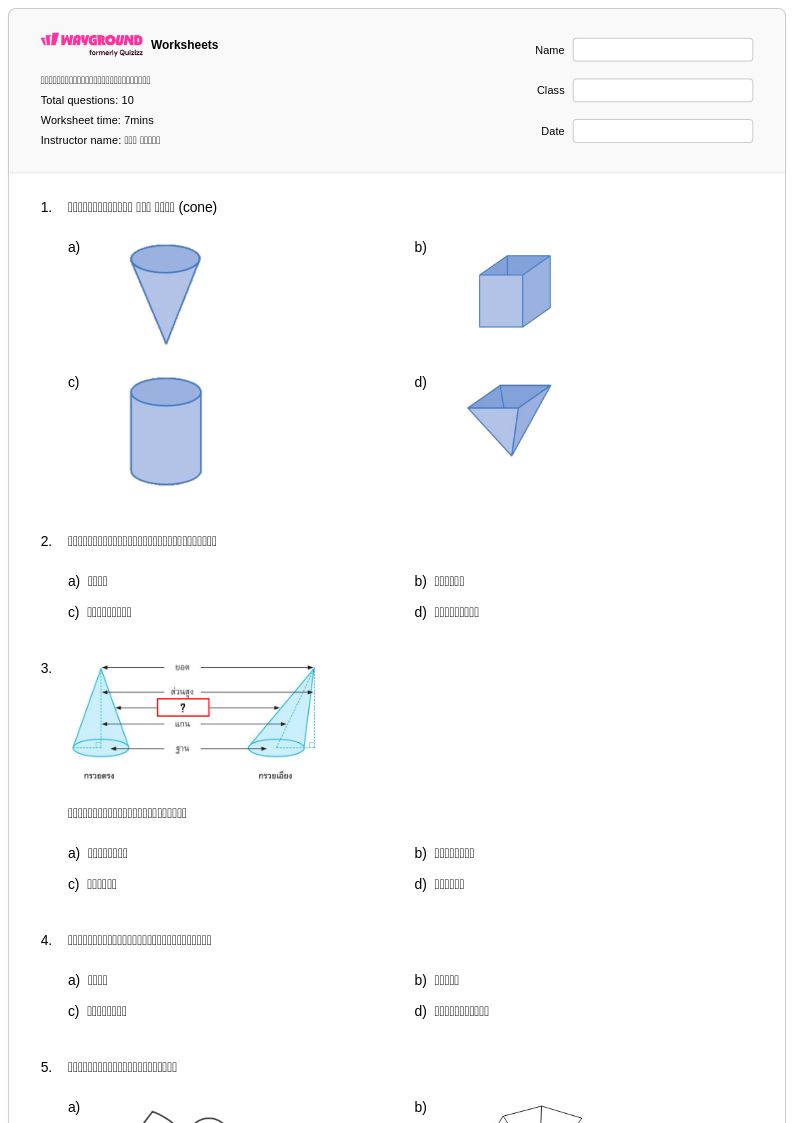
10 P
1st - 9th
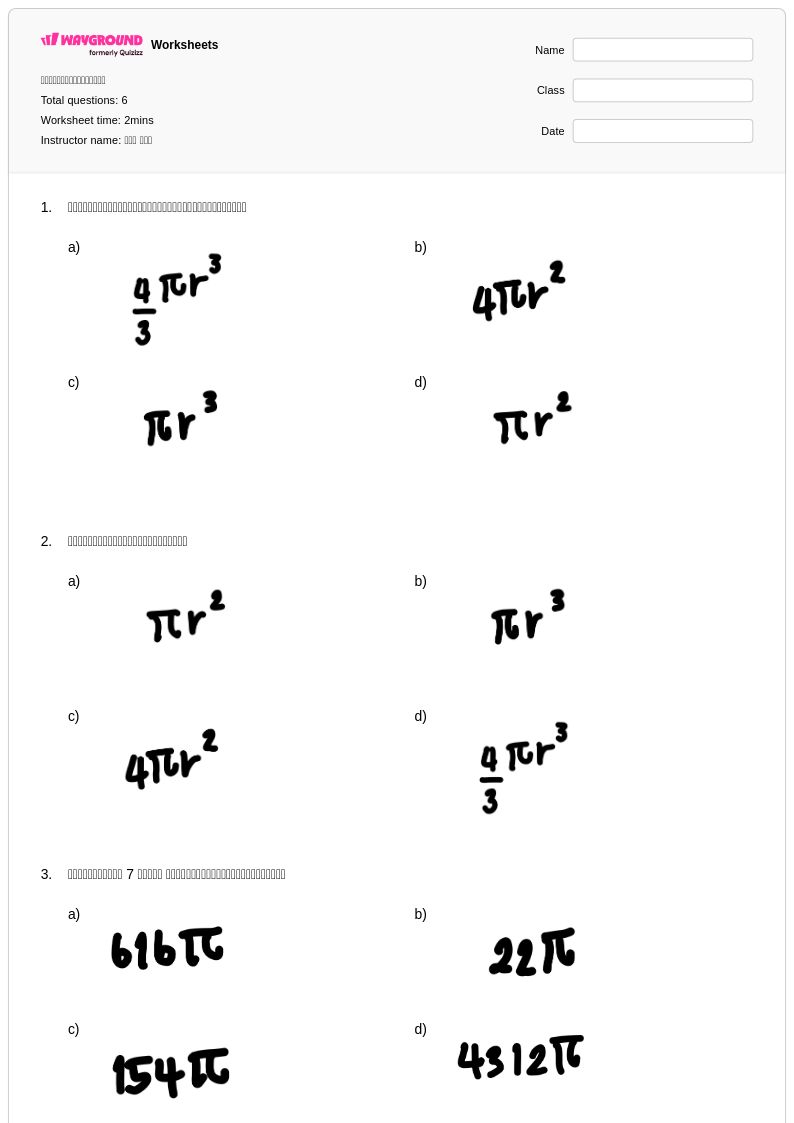
6 P
6th - 12th
Przeglądaj พื้นที่ผิว arkusze ćwiczeń według ocen
Przeglądaj inne arkusze tematyczne dla ระดับ 6
สำรวจแผ่นงาน พื้นที่ผิว ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 6
แบบฝึกหัดพื้นที่ผิวสำหรับนักเรียนชั้นประถมศึกษาปีที่ 6 จาก Wayground (เดิมชื่อ Quizizz) ให้แบบฝึกหัดที่ครอบคลุมเกี่ยวกับการคำนวณพื้นที่ทั้งหมดของรูปทรงสามมิติ รวมถึงปริซึมสี่เหลี่ยม ปริซึมสามเหลี่ยม และพีระมิด แบบฝึกหัดที่ออกแบบมาอย่างเชี่ยวชาญเหล่านี้ช่วยเสริมสร้างทักษะการให้เหตุผลทางเรขาคณิตที่สำคัญ โดยแนะนำนักเรียนผ่านวิธีการที่เป็นระบบในการหาพื้นที่ผิวโดยใช้แบบจำลอง สูตร และกลยุทธ์การแยกส่วนด้วยภาพ แบบฝึกหัดแต่ละชุดประกอบด้วยโจทย์ฝึกหัดโดยละเอียดที่ค่อยๆ ยากขึ้นจากปริซึมสี่เหลี่ยมพื้นฐานไปจนถึงรูปทรงผสมที่ซับซ้อนมากขึ้น พร้อมเฉลยคำตอบที่สมบูรณ์เพื่อสนับสนุนการเรียนรู้ด้วยตนเองและการประเมินตนเอง แบบฝึกหัดเหล่านี้มีให้ใช้งานฟรีในรูปแบบ PDF ที่สะดวก ช่วยให้นักเรียนเชี่ยวชาญแนวคิดพื้นฐานของการวัดพื้นที่ผิวซึ่งมีความสำคัญต่อความสำเร็จในหัวข้อเรขาคณิตขั้นสูง
Wayground (เดิมชื่อ Quizizz) เสริมศักยภาพให้ครูผู้สอนด้วยแบบฝึกหัดพื้นที่ผิวที่สร้างโดยครูหลายล้านรายการ ซึ่งช่วยลดความซับซ้อนในการวางแผนบทเรียนและการสอนที่แตกต่างกันสำหรับห้องเรียนคณิตศาสตร์ชั้นประถมศึกษาปีที่ 6 แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานหลักสูตรและวัตถุประสงค์การเรียนรู้ได้อย่างรวดเร็ว ในขณะที่เครื่องมือปรับแต่งในตัวช่วยให้สามารถปรับเปลี่ยนแบบฝึกหัดได้อย่างราบรื่นเพื่อให้เหมาะกับความต้องการและระดับความสามารถของนักเรียนที่หลากหลาย แบบฝึกหัดที่ครอบคลุมเหล่านี้มีให้เลือกทั้งในรูปแบบไฟล์ PDF ที่สามารถพิมพ์ได้สำหรับการใช้งานในห้องเรียนแบบดั้งเดิม และเวอร์ชันดิจิทัลแบบโต้ตอบที่ให้ผลตอบรับทันที ทำให้มีคุณค่าอย่างยิ่งสำหรับการเรียนเสริม การเสริมสร้างความรู้ และการฝึกฝนทักษะเฉพาะด้าน ครูสามารถจัดระเบียบแบบฝึกหัดเกี่ยวกับพื้นที่ผิวในระดับความยากต่างๆ ได้อย่างมีประสิทธิภาพ ทำให้มั่นใจได้ว่านักเรียนทุกคนจะได้รับความท้าทายและการสนับสนุนที่เหมาะสมในขณะที่สร้างความเข้าใจเชิงแนวคิดเกี่ยวกับเรขาคณิตสามมิติ
