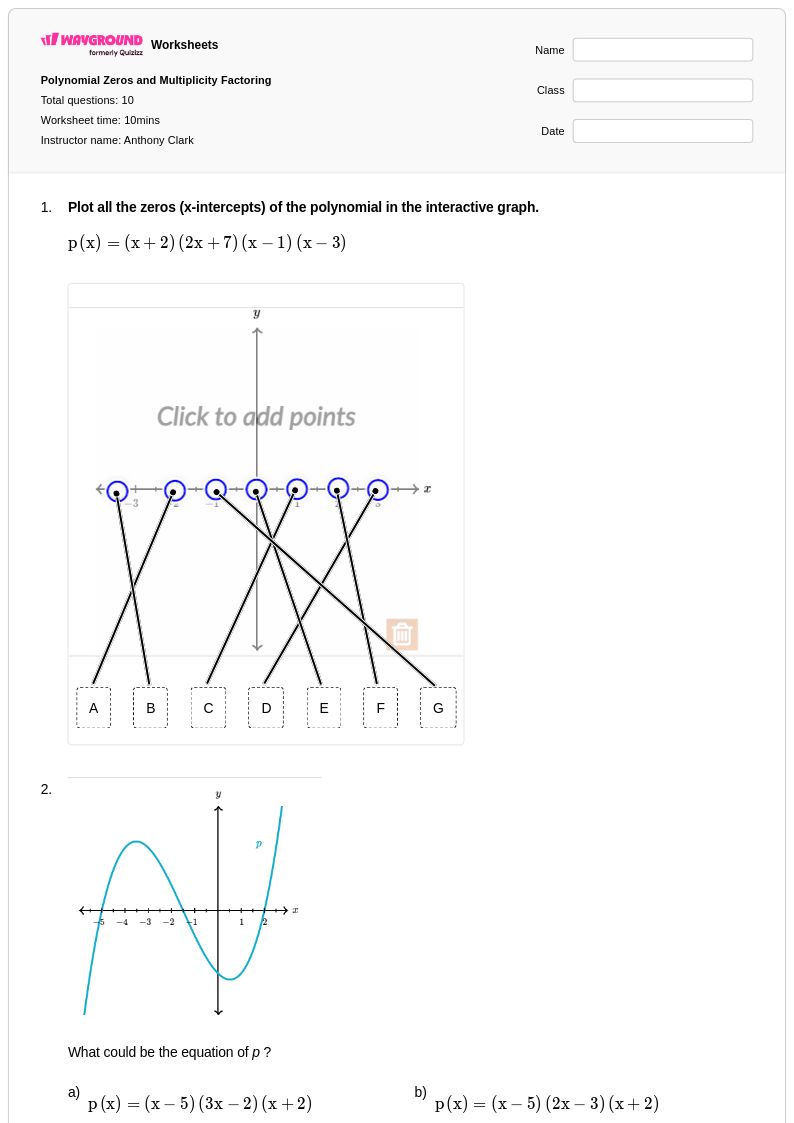
10 คิว
11th - Uni

21 คิว
10th
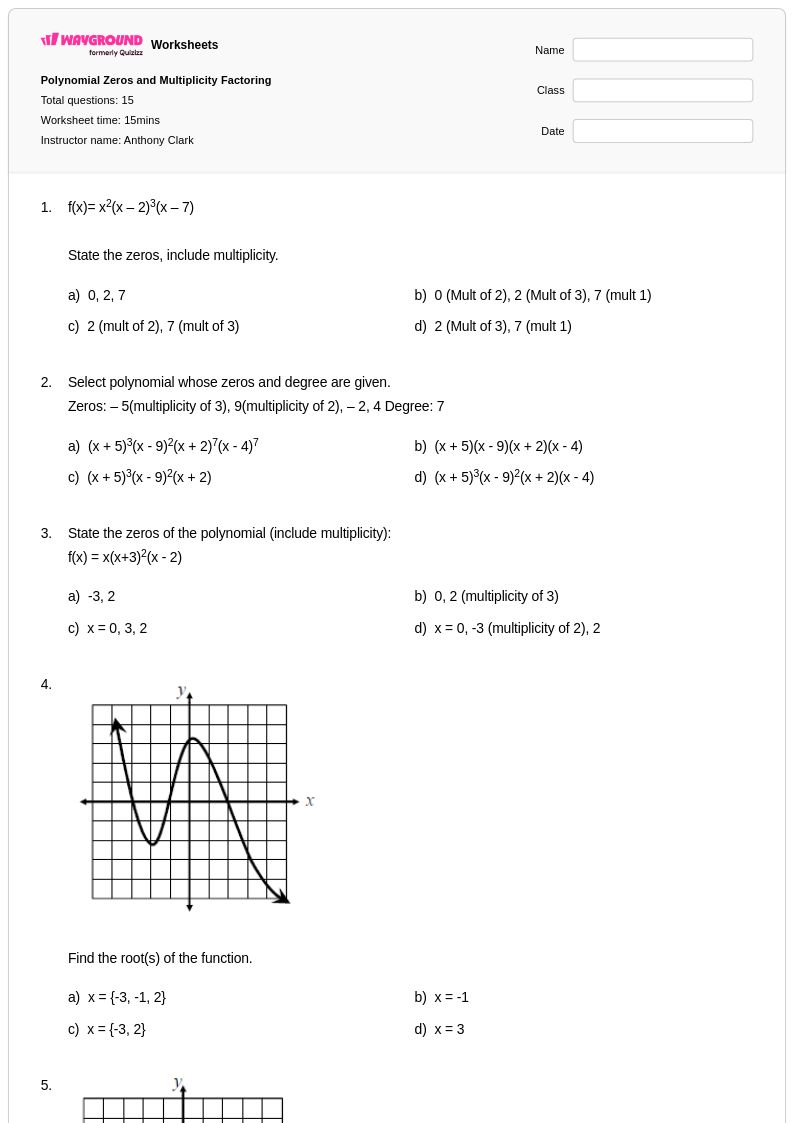
15 คิว
11th - Uni
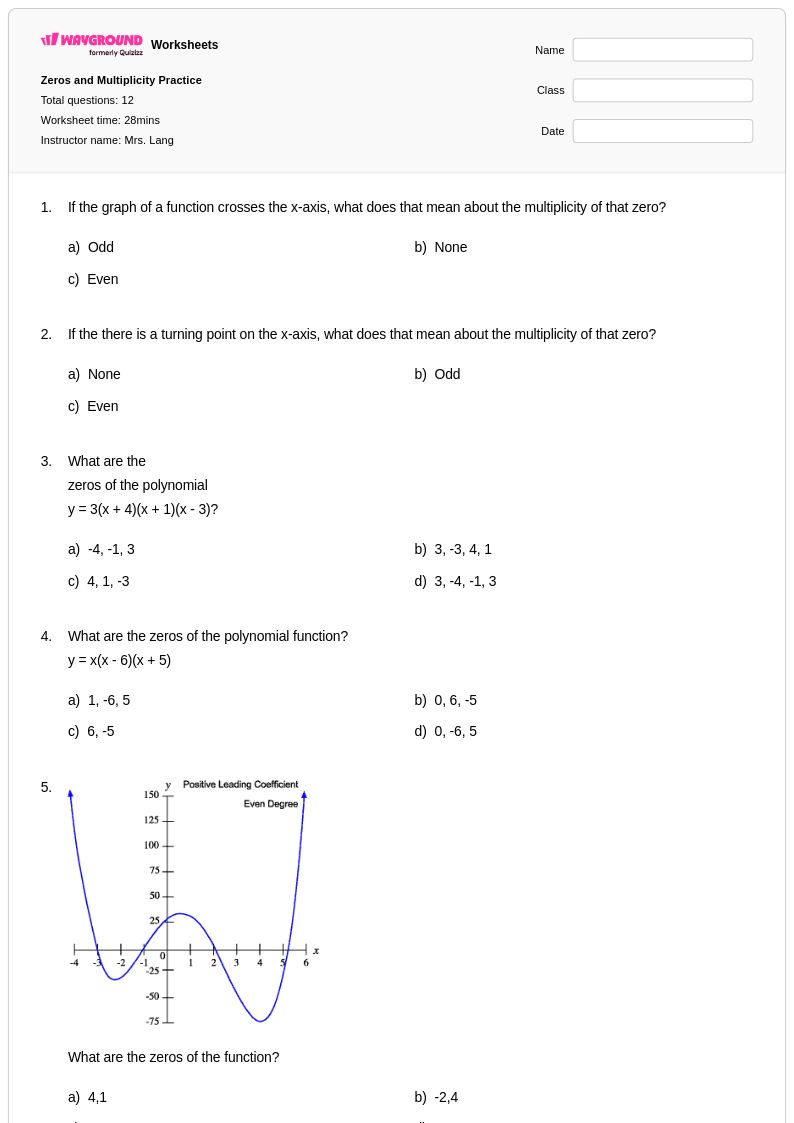
12 คิว
9th - 10th

20 คิว
11th - Uni
38 คิว
9th - Uni

20 คิว
9th - Uni
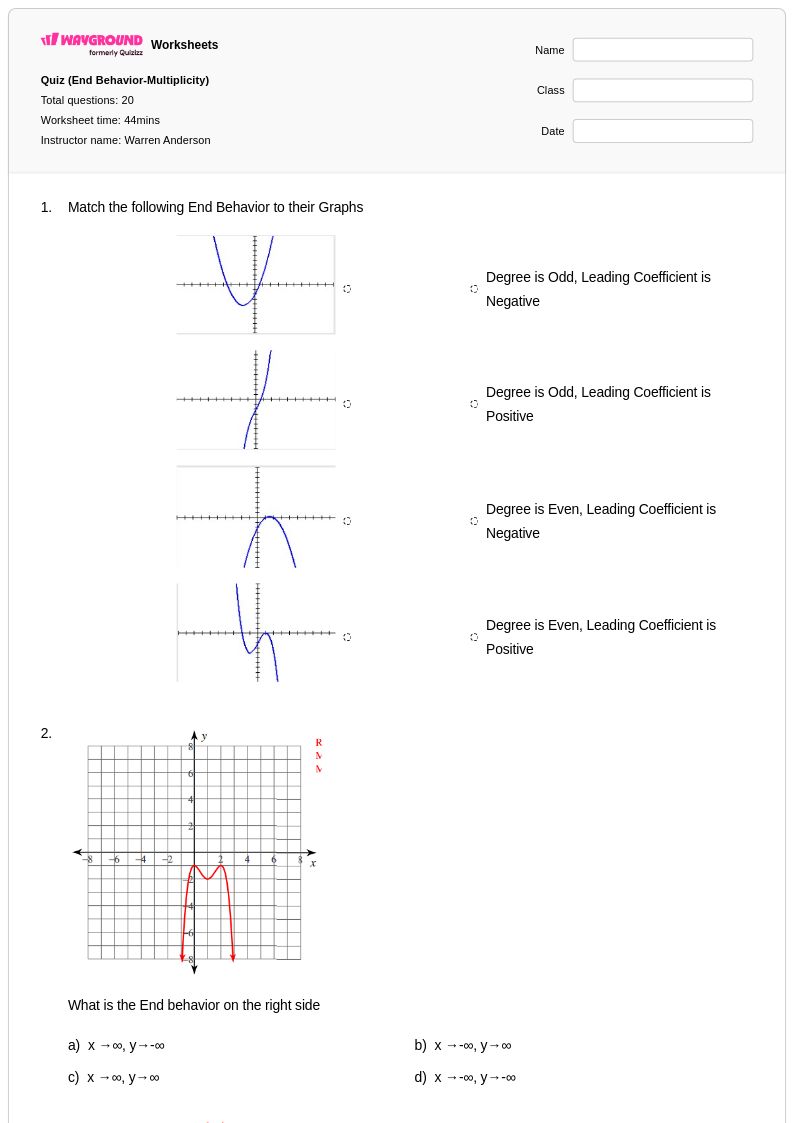
20 คิว
9th - 12th
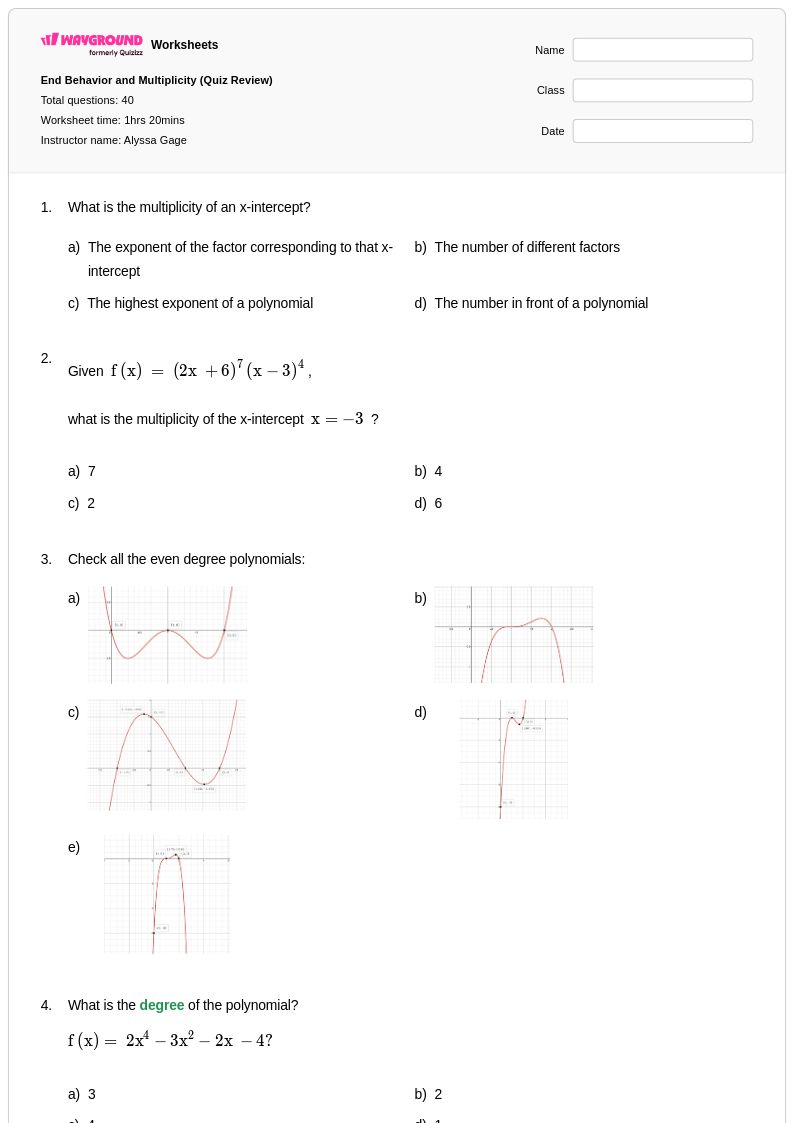
40 คิว
10th
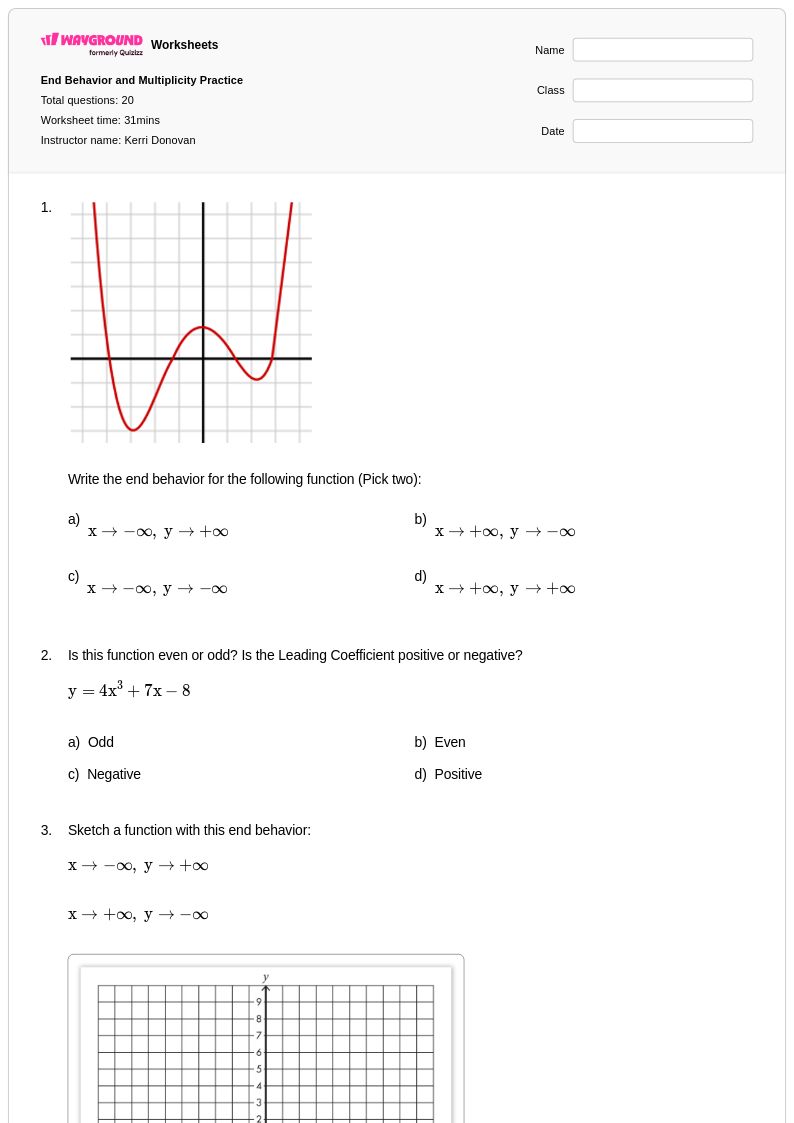
20 คิว
11th
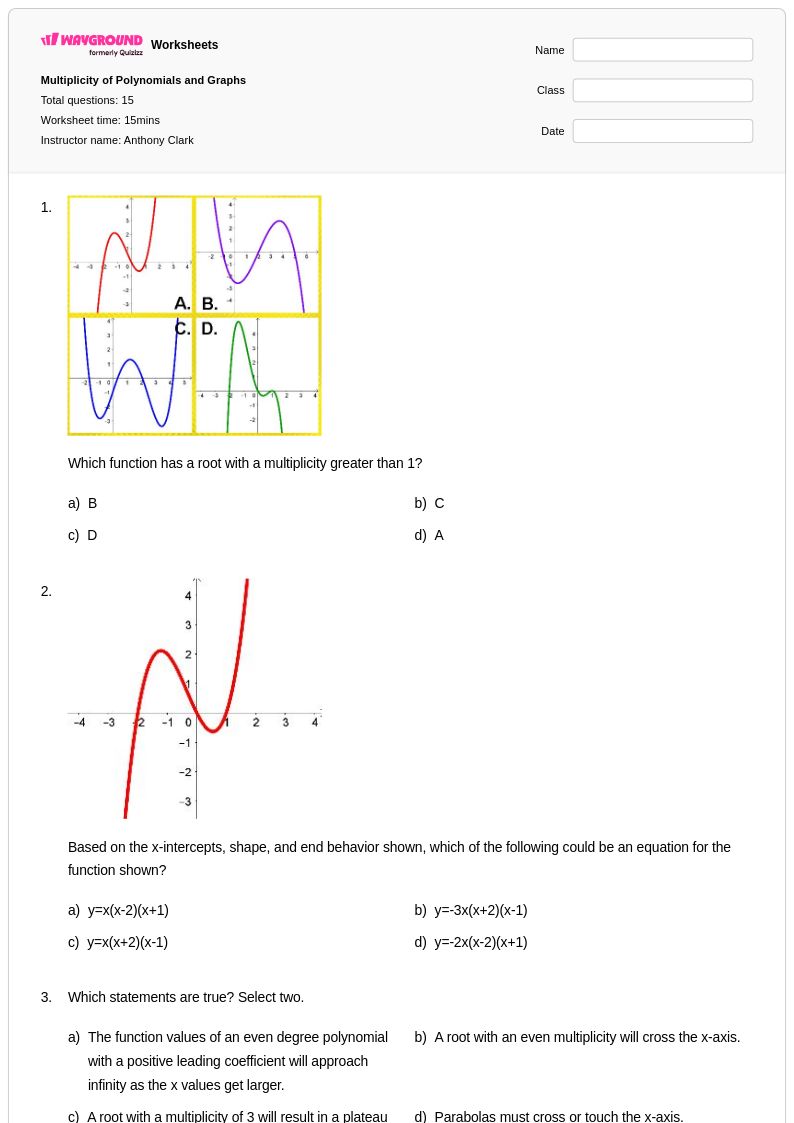
15 คิว
11th - Uni
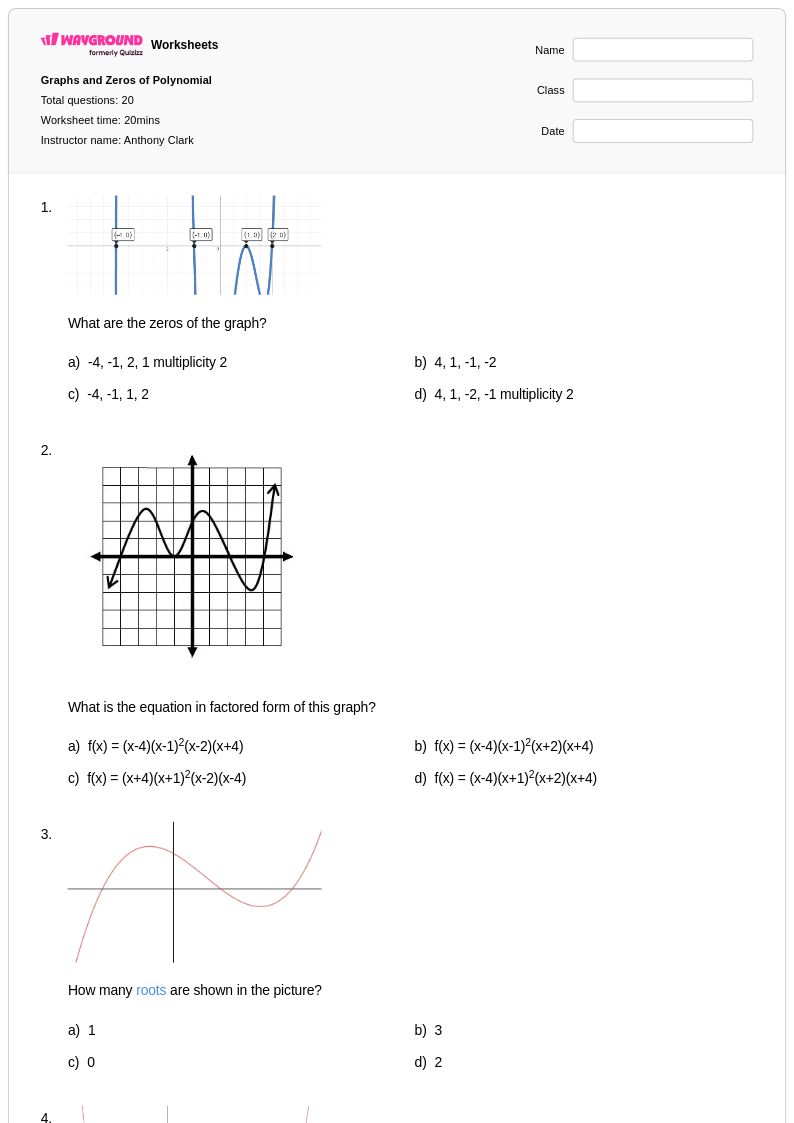
20 คิว
11th - Uni
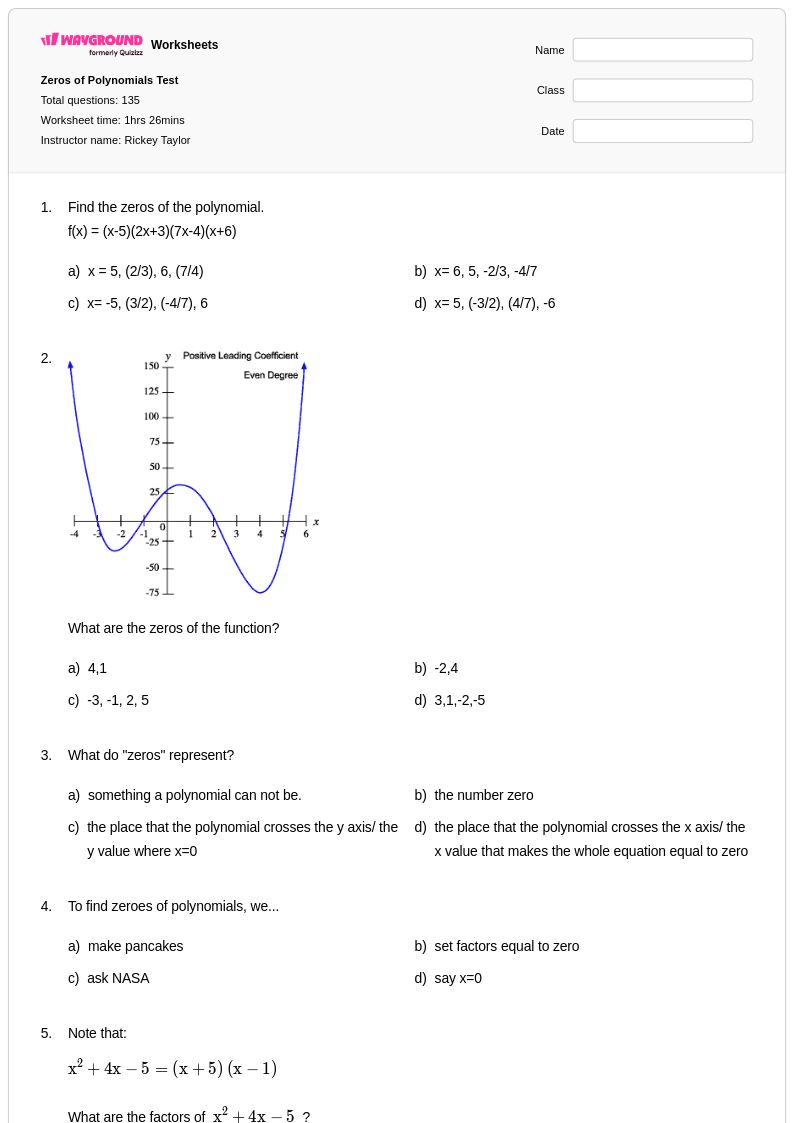
135 คิว
9th - 12th
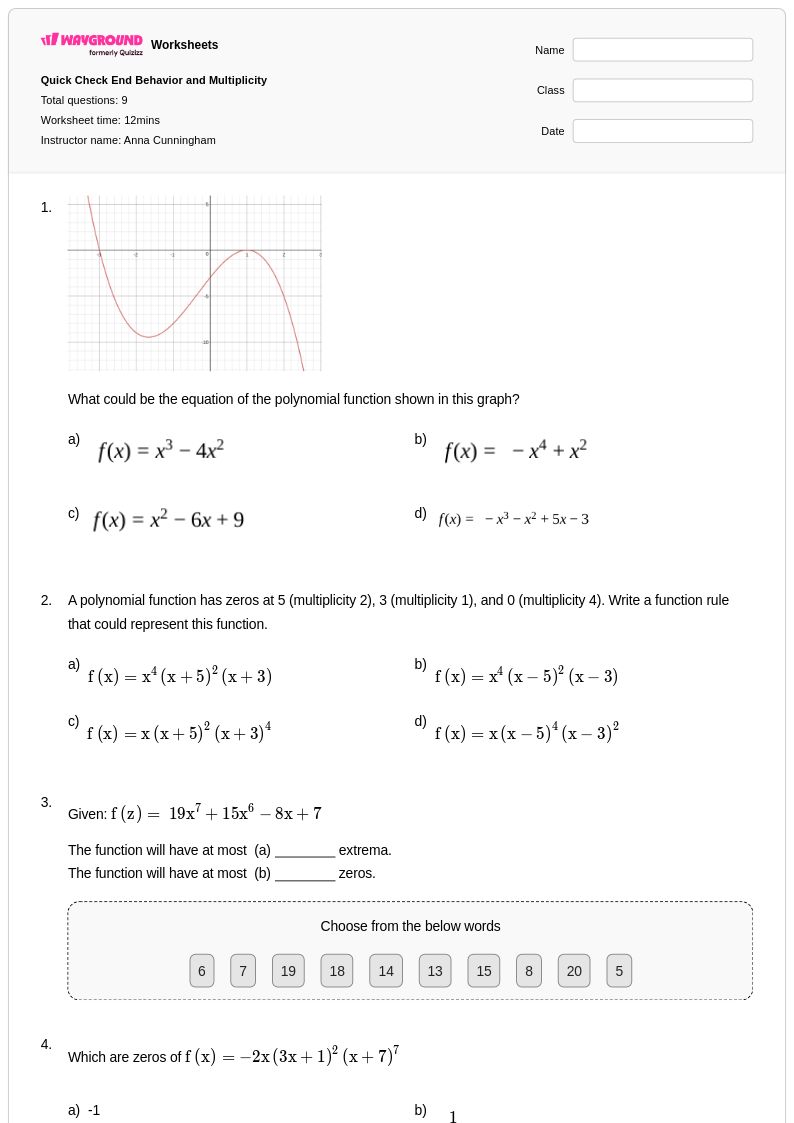
9 คิว
12th
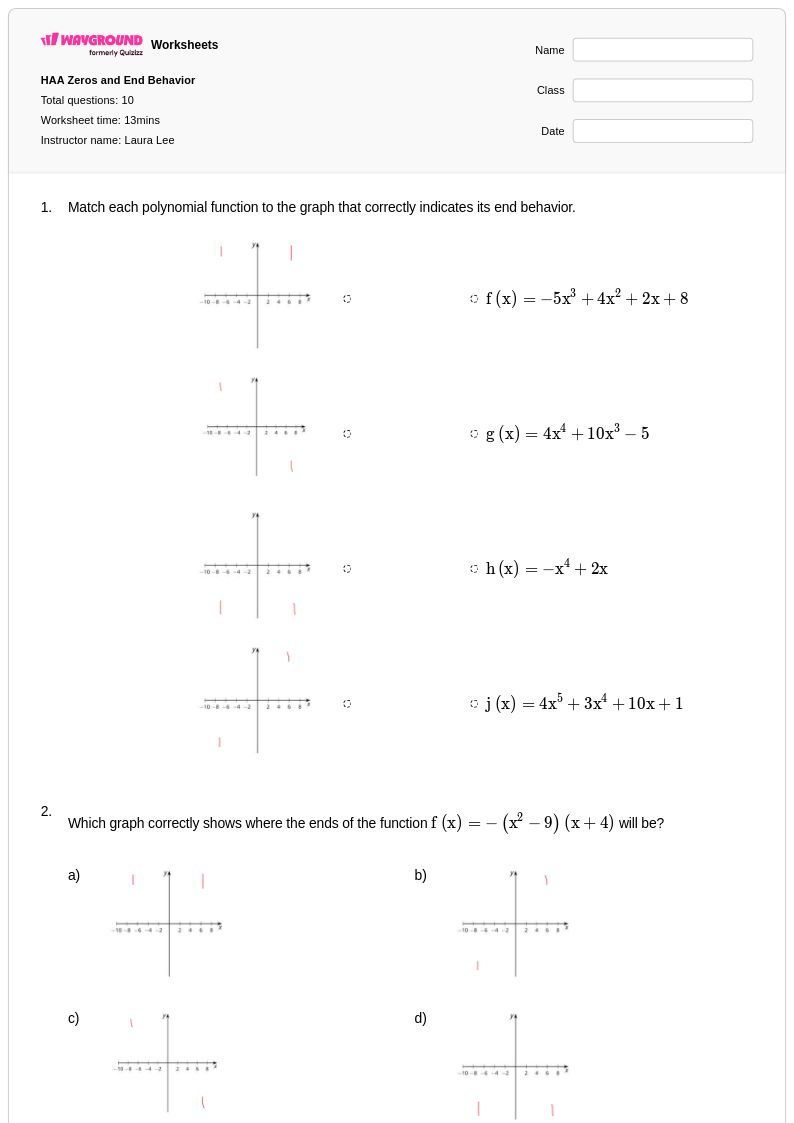
10 คิว
9th - 12th

18 คิว
11th

77 คิว
11th

20 คิว
11th - Uni

15 คิว
12th
20 คิว
11th
12 คิว
11th

20 คิว
11th - Uni
19 คิว
11th
สำรวจแผ่นงานตามหัวเรื่อง
สำรวจแผ่นงาน ศูนย์และความซ้ำซ้อน ที่พิมพ์ได้
แบบฝึกหัดเรื่องศูนย์และความซ้ำซ้อนจาก Wayground (เดิมคือ Quizizz) เป็นแบบฝึกหัดที่ครอบคลุมสำหรับนักเรียนที่กำลังเรียนรู้การระบุและวิเคราะห์พฤติกรรมของฟังก์ชันพหุนามที่จุดตัดแกน x แหล่งข้อมูลที่ออกแบบมาอย่างเชี่ยวชาญเหล่านี้ช่วยให้นักเรียนเข้าใจแนวคิดสำคัญที่ว่า เมื่อพหุนามมีตัวประกอบเป็น (x - a)^n กราฟจะสัมผัสหรือตัดแกน x ที่ x = a โดยมีพฤติกรรมที่คาดการณ์ได้เฉพาะเจาะจงซึ่งกำหนดโดยเลขชี้กำลัง n แบบฝึกหัดในชุดนี้ช่วยสร้างความเข้าใจอย่างเป็นระบบว่า ความซ้ำซ้อนที่เป็นเลขคี่สร้างจุดตัดแกน x ที่กราฟตัดแกน ในขณะที่ความซ้ำซ้อนที่เป็นเลขคู่สร้างจุดที่กราฟสัมผัสแกนและวกกลับ แบบฝึกหัดแต่ละชุดมีเฉลยโดยละเอียดที่ช่วยแนะนำนักเรียนตลอดกระบวนการแยกตัวประกอบพหุนาม การระบุศูนย์ การกำหนดความซ้ำซ้อน และการร่างกราฟที่สอดคล้องกัน พร้อมตัวเลือกไฟล์ PDF ที่พิมพ์ได้ฟรีสำหรับการใช้งานในห้องเรียนและการบ้าน
Wayground (เดิมชื่อ Quizizz) ช่วยเสริมศักยภาพครูคณิตศาสตร์ด้วยแหล่งข้อมูลที่สร้างโดยครูหลายล้านรายการ โดยเน้นเฉพาะเรื่องค่าศูนย์และแนวคิดเรื่องความคูณ มีฟังก์ชันการค้นหาและการกรองที่มีประสิทธิภาพ ช่วยให้ครูค้นหาแบบฝึกหัดที่ตรงกับความต้องการในการสอนได้อย่างแม่นยำ เนื้อหาของแพลตฟอร์มสอดคล้องกับมาตรฐาน ทำให้แบบฝึกหัดพีชคณิตเหล่านี้ตรงตามข้อกำหนดของหลักสูตร พร้อมทั้งมีเครื่องมือสำหรับการปรับวิธีการสอนให้เหมาะสมกับระดับการเรียนรู้ที่หลากหลายในห้องเรียน ครูสามารถปรับแต่งแบบฝึกหัดที่มีอยู่หรือสร้างแบบฝึกหัดใหม่ได้อย่างง่ายดาย ด้วยตัวเลือกที่ยืดหยุ่นทั้งในรูปแบบไฟล์ PDF ที่พิมพ์ได้และแบบฝึกหัดดิจิทัลแบบโต้ตอบที่ช่วยให้ได้รับข้อเสนอแนะและการประเมินผลได้ทันที คุณสมบัติที่ครอบคลุมเหล่านี้ช่วยให้การวางแผนบทเรียนง่ายขึ้น โดยจัดเตรียมสื่อพร้อมใช้งานสำหรับการสอนเบื้องต้น การแก้ไขปัญหาเฉพาะหน้าสำหรับนักเรียนที่ประสบปัญหา และกิจกรรมเสริมสำหรับผู้เรียนที่มีความสามารถสูง ซึ่งท้ายที่สุดแล้วจะช่วยสนับสนุนการฝึกฝนทักษะที่มีประสิทธิภาพซึ่งสร้างความมั่นใจให้กับนักเรียนในการวิเคราะห์พฤติกรรมของฟังก์ชันพหุนามที่ค่าศูนย์
