
14 คิว
7th

20 คิว
7th

16 คิว
7th

20 คิว
7th - 11th

24 คิว
7th
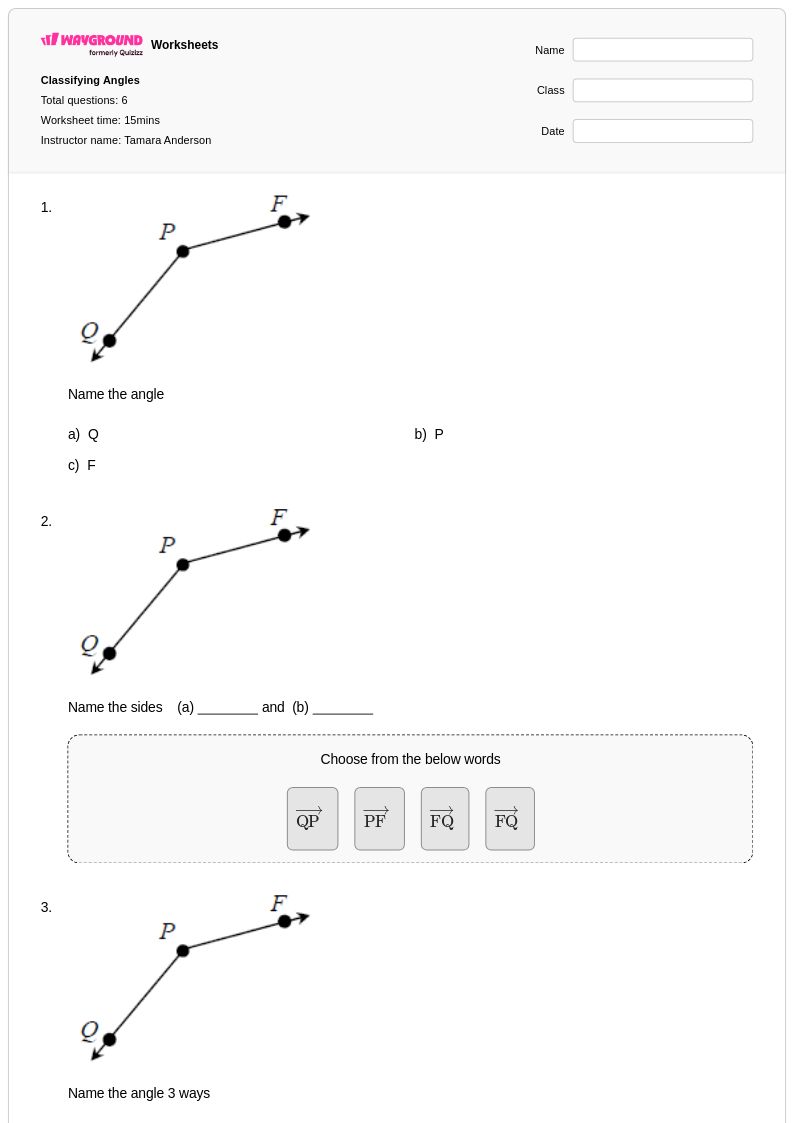
6 คิว
7th

20 คิว
7th
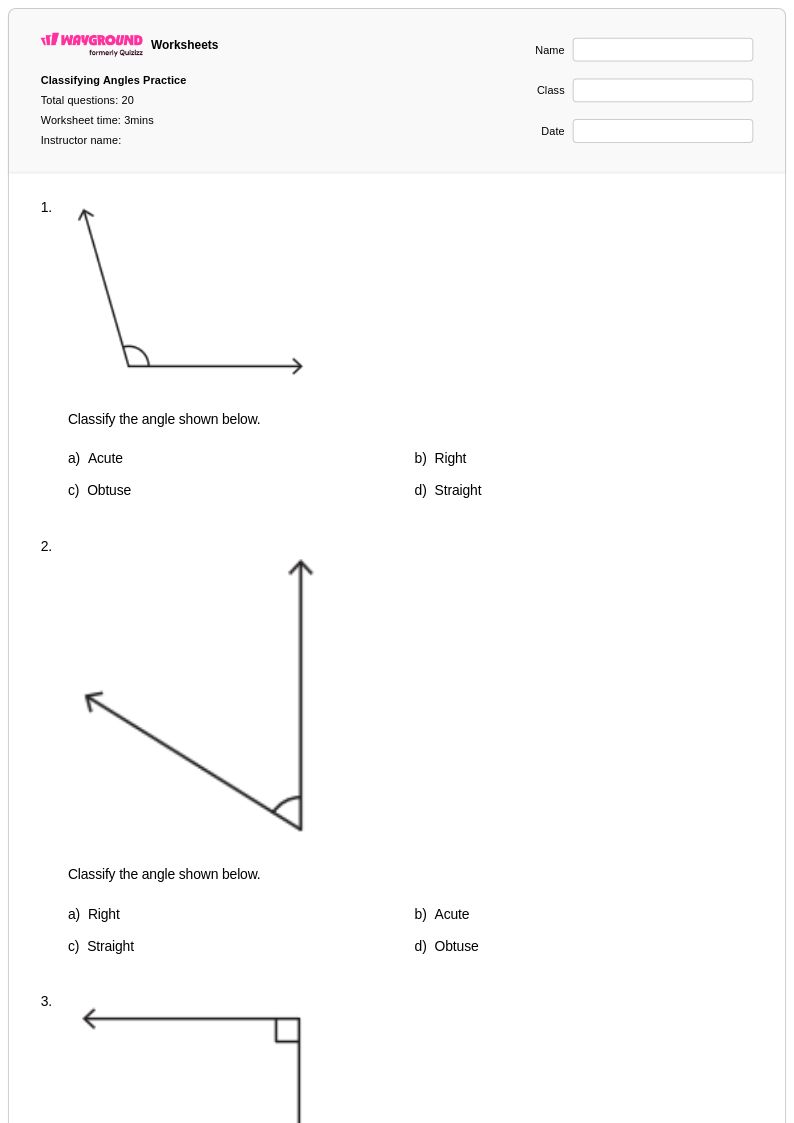
20 คิว
7th - 10th

15 คิว
7th
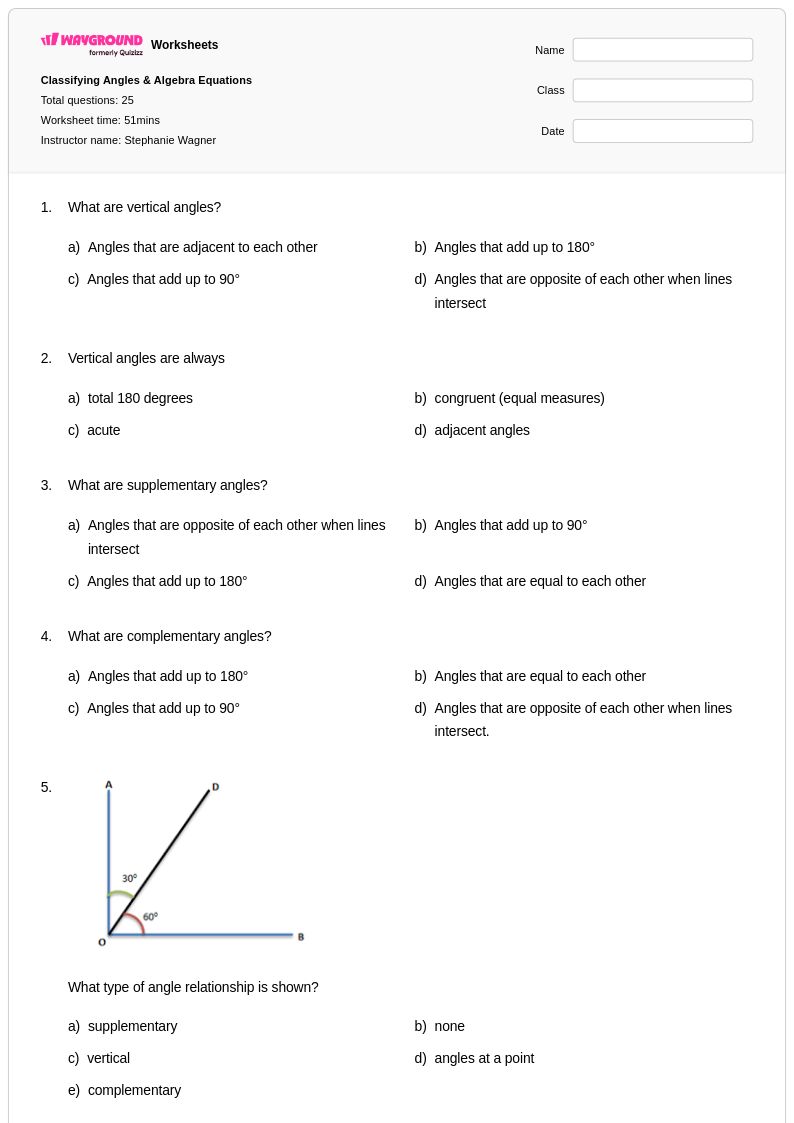
25 คิว
7th
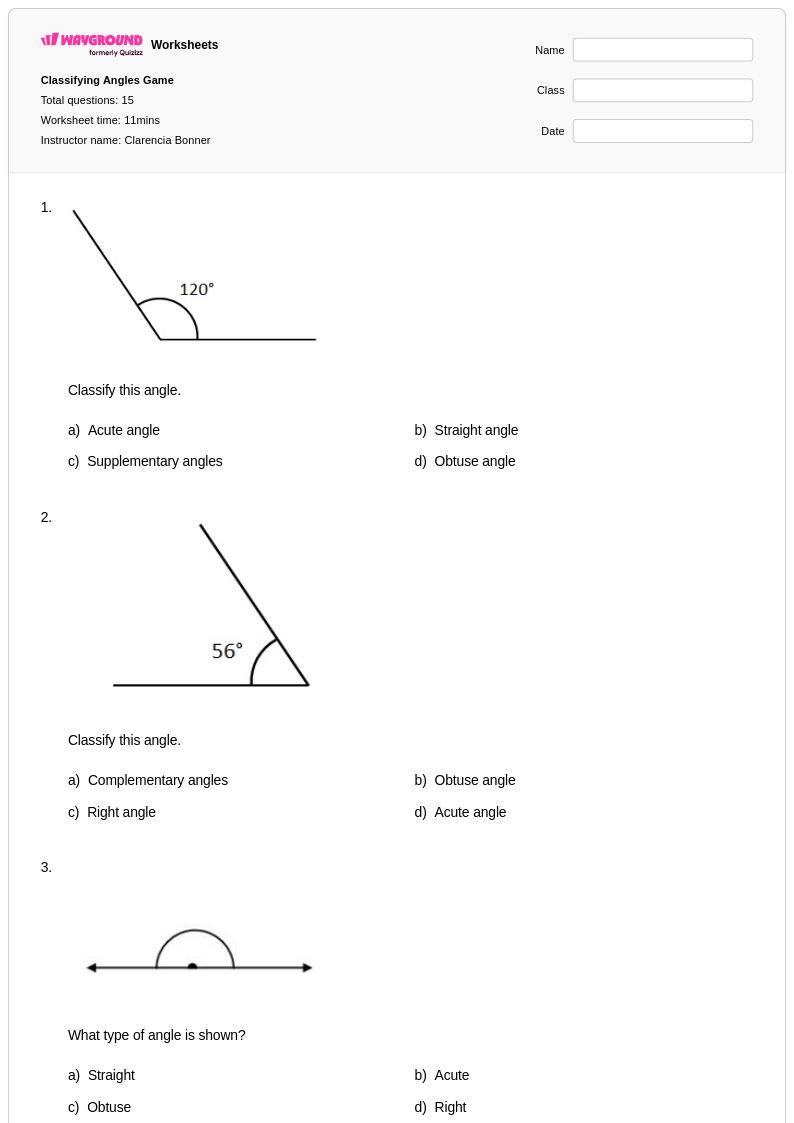
15 คิว
7th
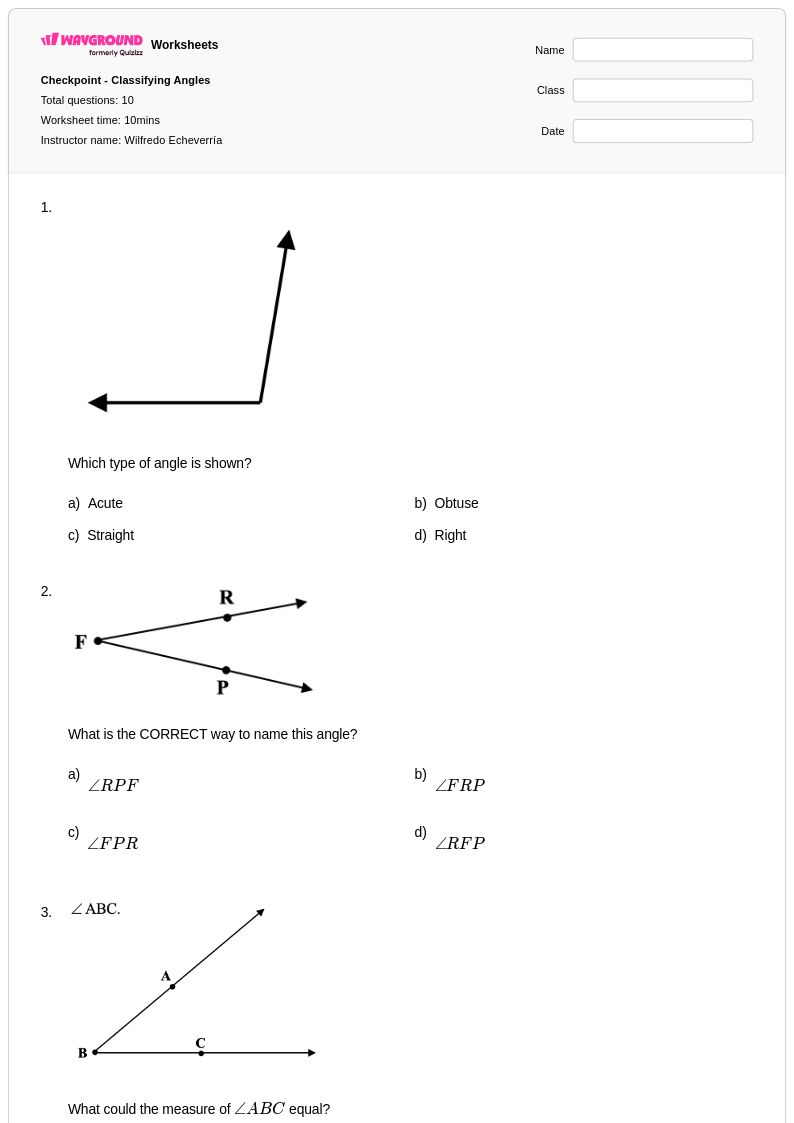
10 คิว
7th
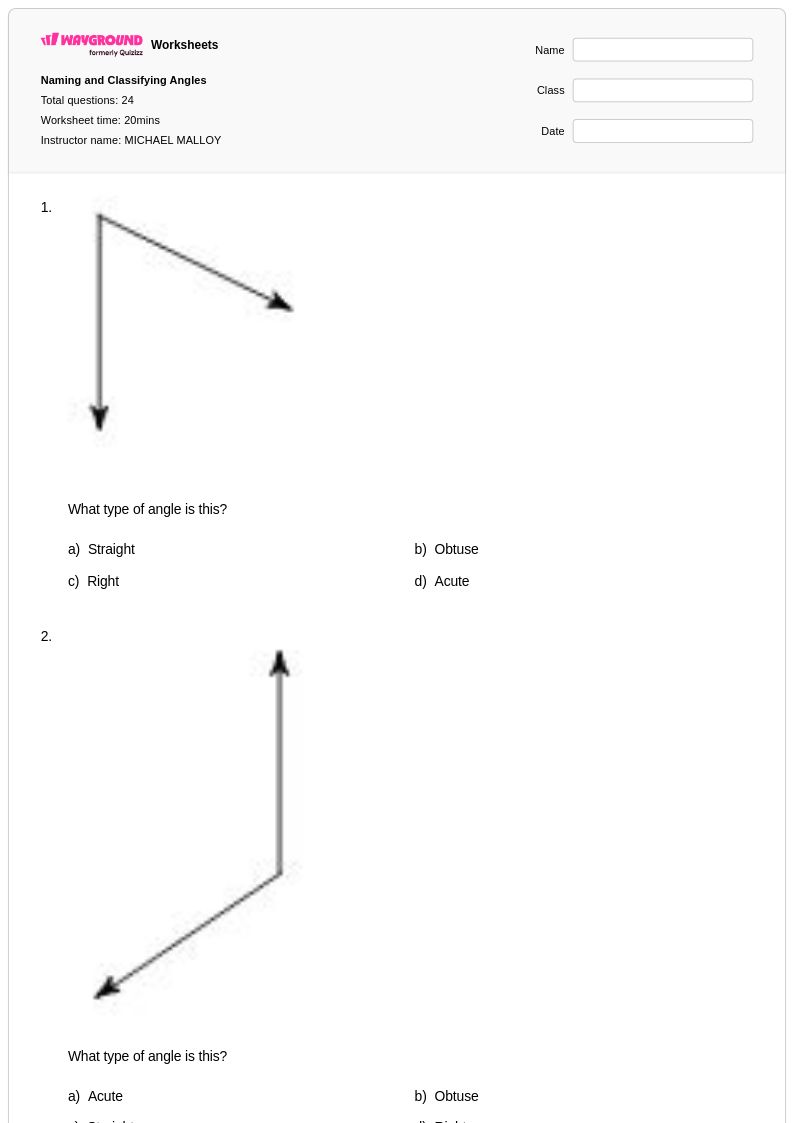
24 คิว
7th
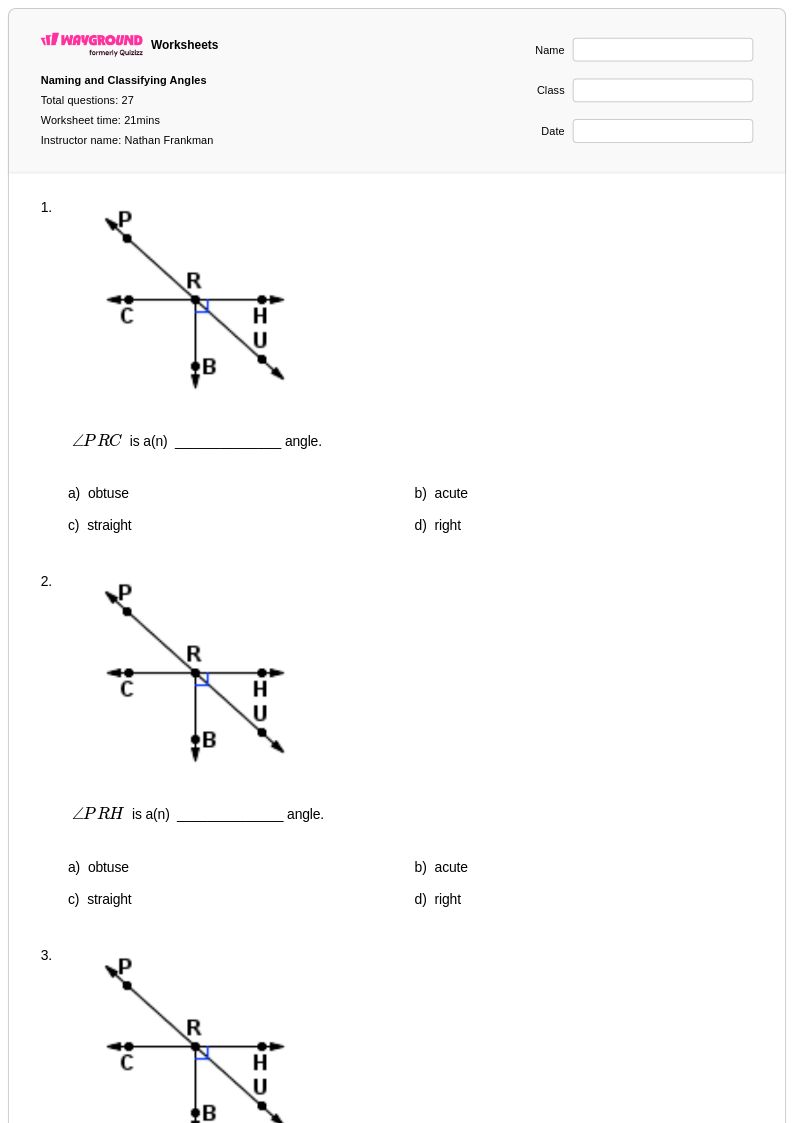
27 คิว
7th - 12th
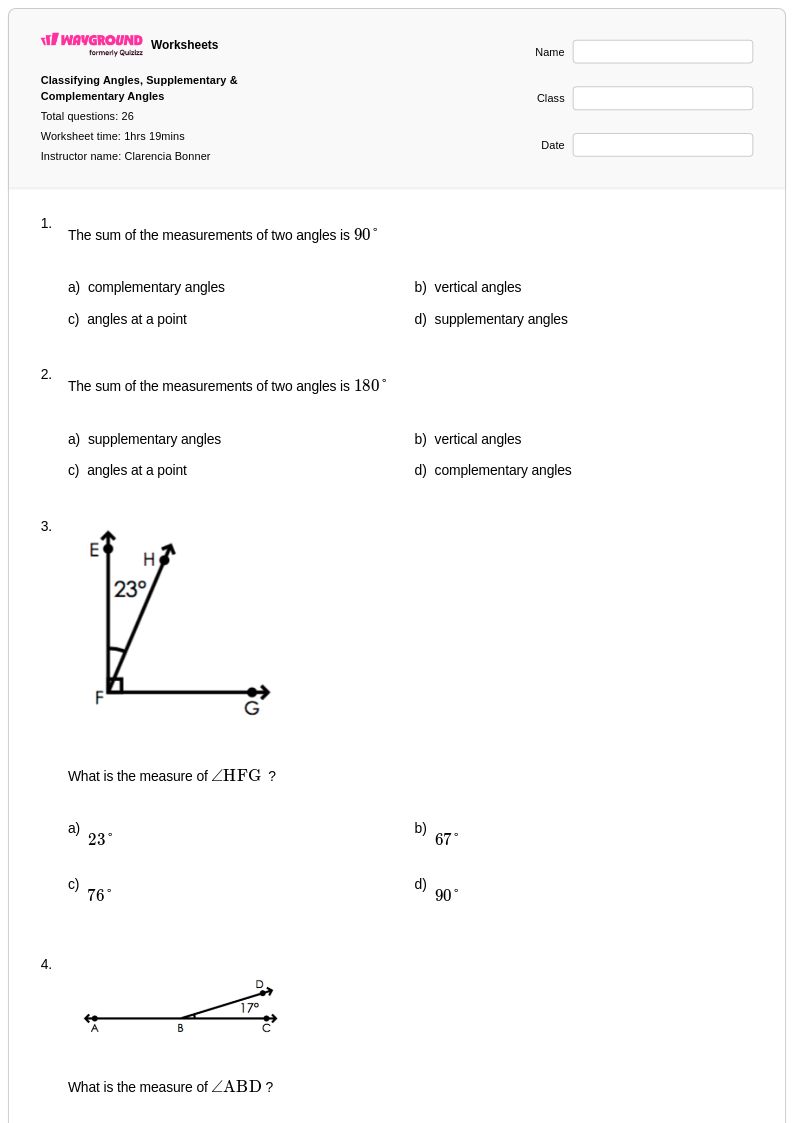
26 คิว
7th
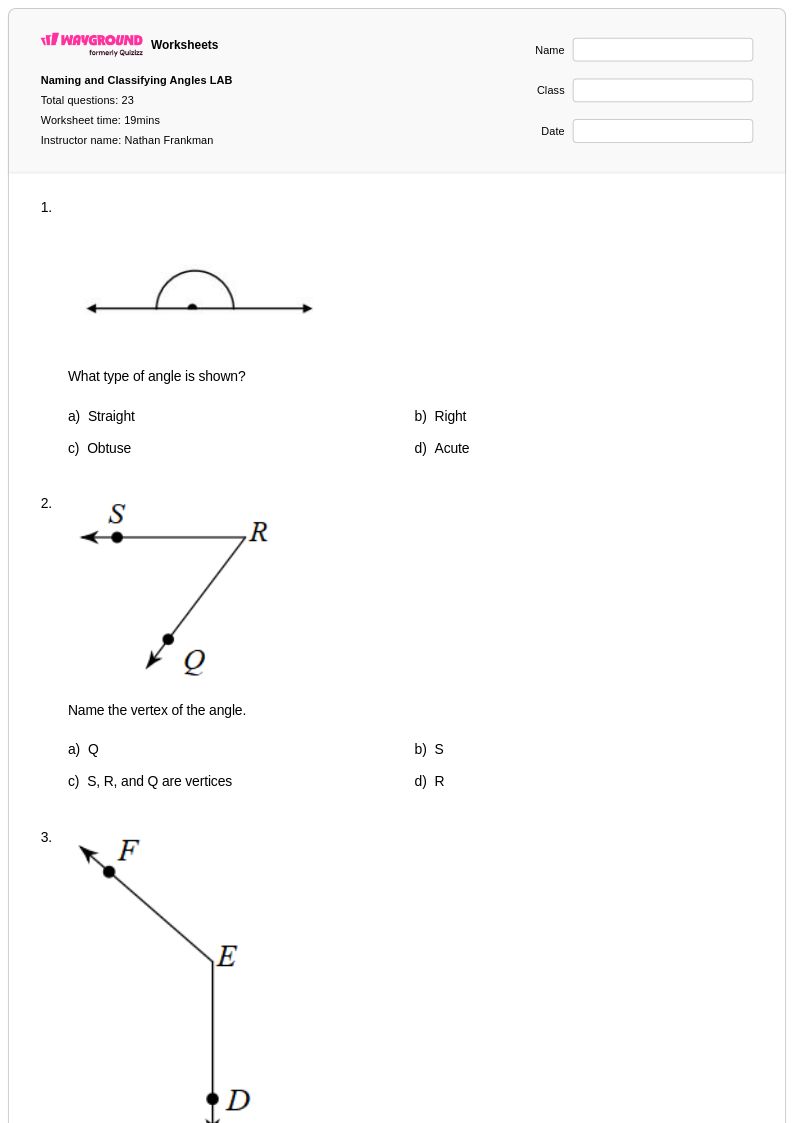
23 คิว
7th - 12th
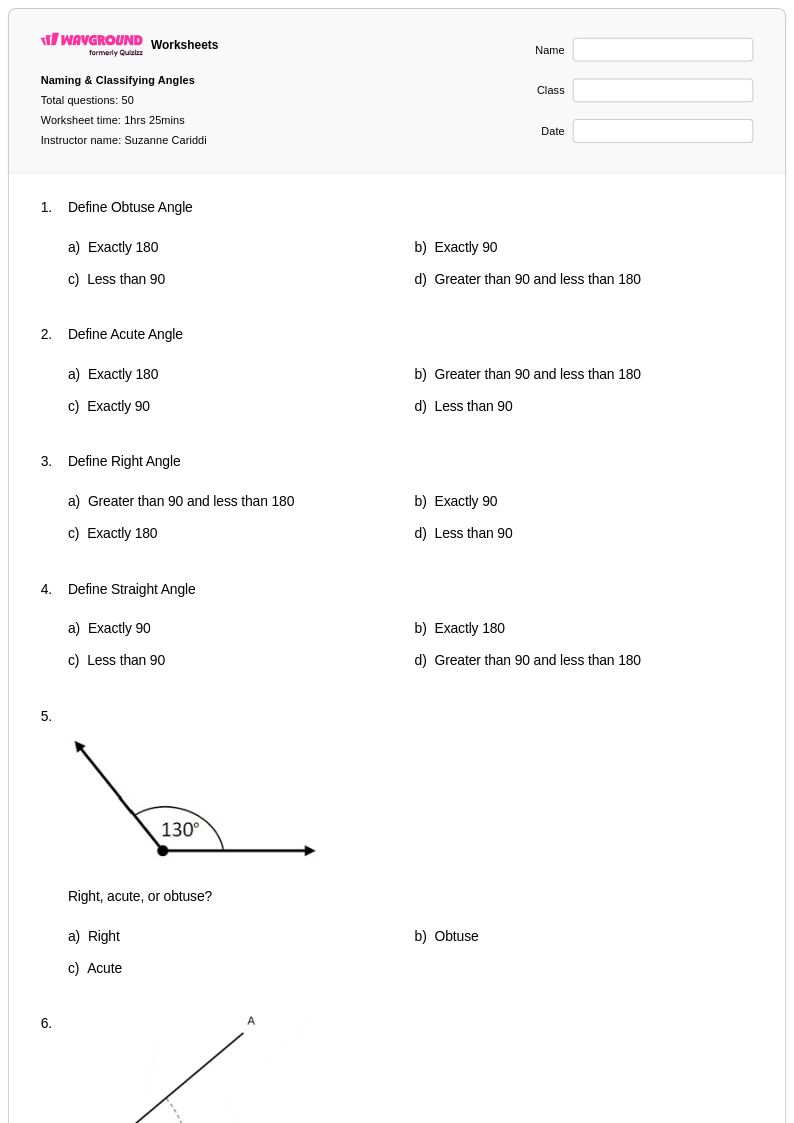
50 คิว
7th - 10th
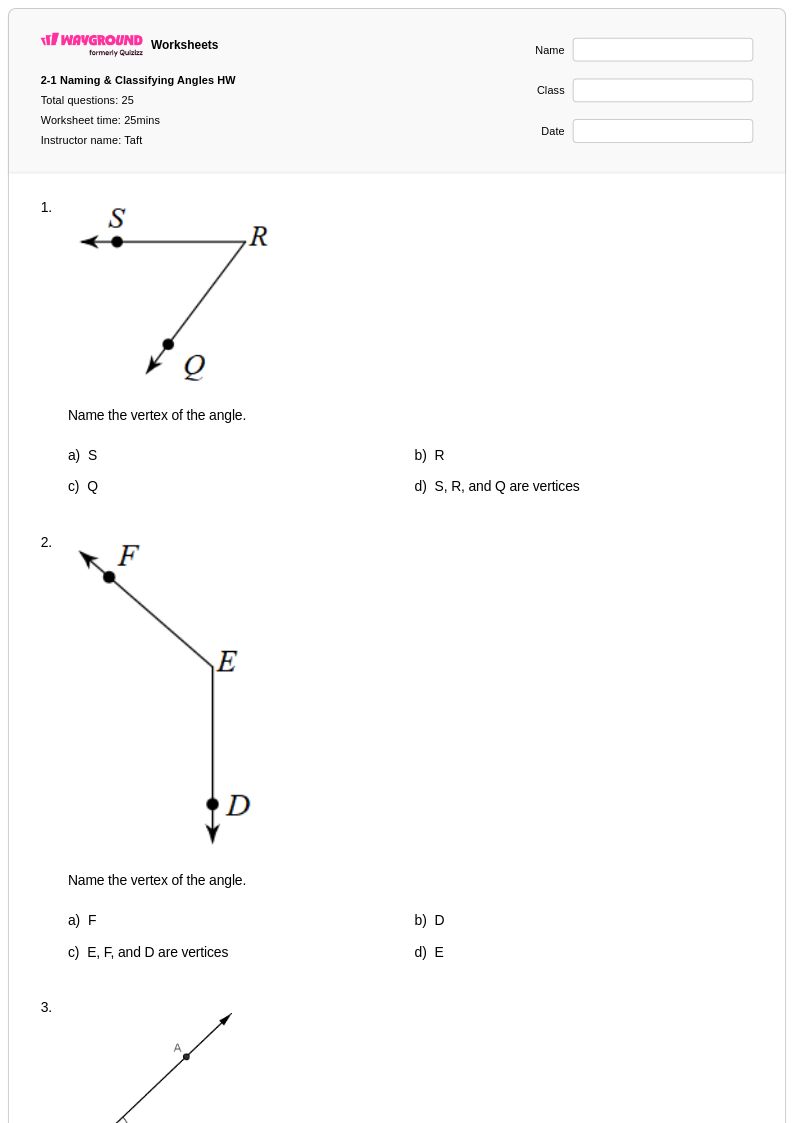
25 คิว
7th - 8th

10 คิว
7th

18 คิว
7th
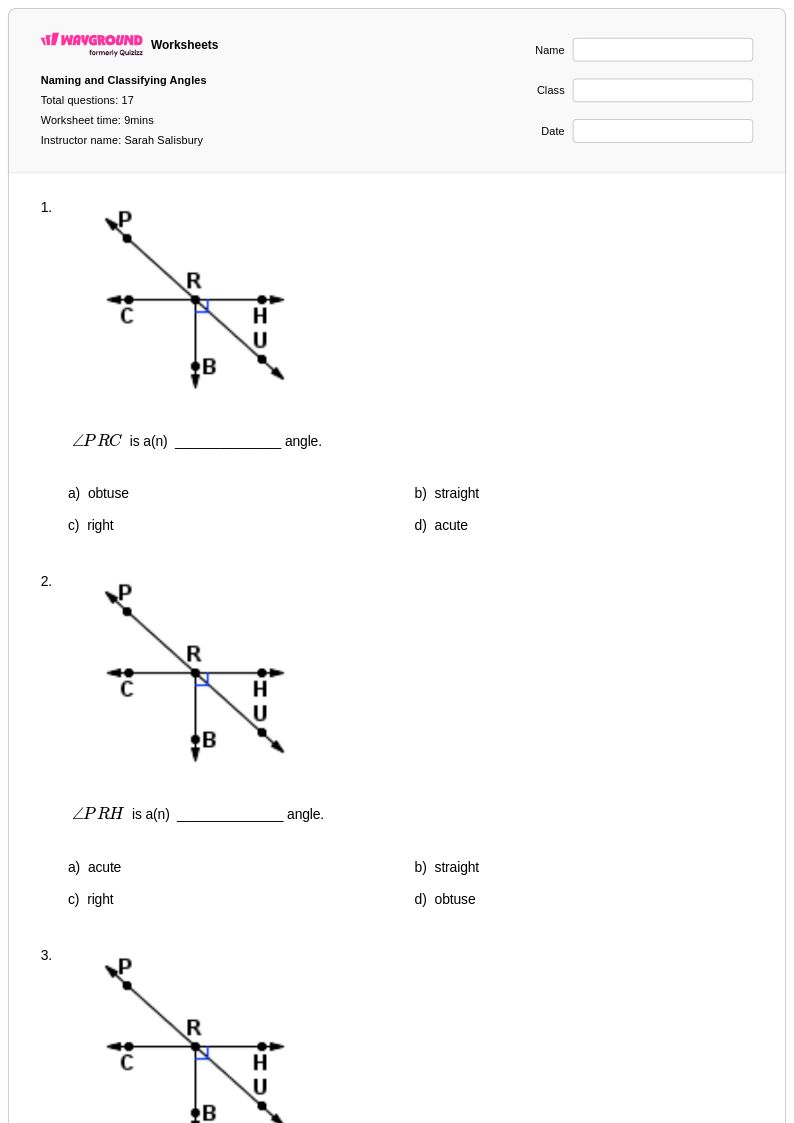
17 คิว
7th - 10th
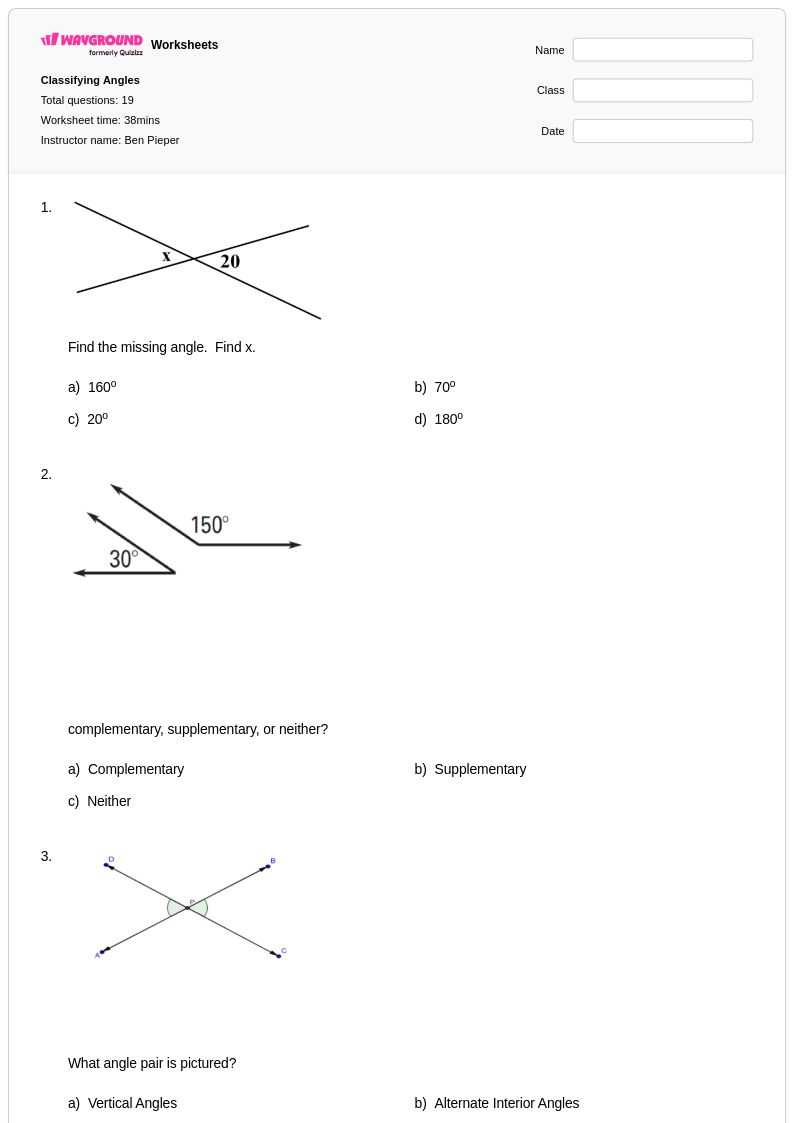
19 คิว
1st - 7th
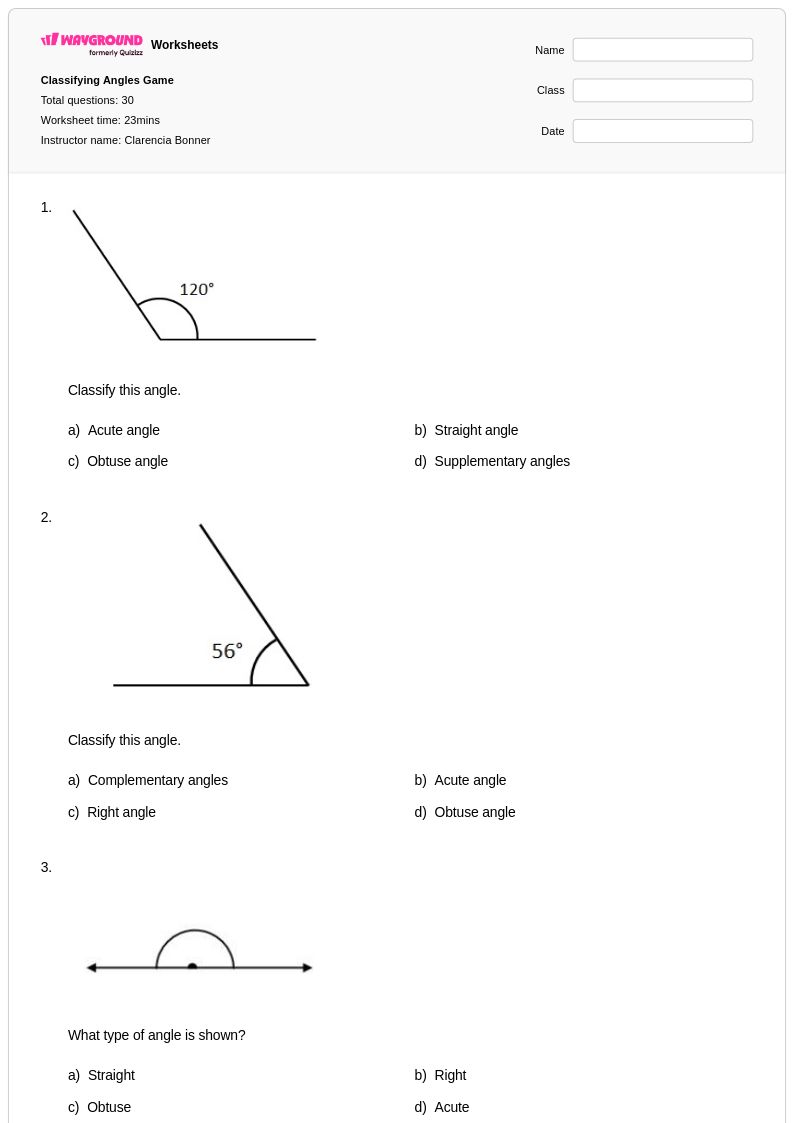
30 คิว
7th
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 7
สำรวจแผ่นงาน การจำแนกประเภทของมุม ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 7
แบบฝึกหัดการจำแนกประเภทมุมสำหรับนักเรียนชั้น ม.1 จาก Wayground (เดิมชื่อ Quizizz) ให้แบบฝึกหัดที่ครอบคลุมในการระบุและจำแนกประเภทมุมต่างๆ โดยพิจารณาจากขนาดและคุณสมบัติ แหล่งข้อมูลทางการศึกษาเหล่านี้ช่วยเสริมสร้างทักษะเรขาคณิตพื้นฐานให้กับนักเรียน โดยแนะนำการจำแนกประเภทมุมแหลม มุมฉาก มุมป้าน มุมตรง และมุมสะท้อนอย่างเป็นระบบ พร้อมทั้งแนะนำแนวคิดเกี่ยวกับความสัมพันธ์ของมุมประกอบและมุมเสริม แบบฝึกหัดมีโจทย์ฝึกหัดที่จัดโครงสร้างอย่างรอบคอบ โดยเริ่มจากการระบุมุมพื้นฐานไปจนถึงสถานการณ์การจำแนกประเภทที่ซับซ้อนมากขึ้น พร้อมด้วยเฉลยคำตอบโดยละเอียดที่สนับสนุนทั้งการเรียนรู้ด้วยตนเองและการเรียนการสอนในห้องเรียน ครูและนักเรียนสามารถเข้าถึงเอกสารที่พิมพ์ได้ฟรีเหล่านี้ในรูปแบบ PDF ที่สะดวก ทำให้เหมาะสำหรับงานบ้าน กิจกรรมในห้องเรียน หรือการเตรียมการประเมินผล
Wayground (เดิมชื่อ Quizizz) ช่วยเสริมศักยภาพให้กับครูผู้สอนด้วยชุดทรัพยากรการจำแนกประเภทมุมที่สร้างโดยครูจำนวนมาก โดยดึงมาจากแบบฝึกหัดคุณภาพสูงนับล้านฉบับที่สอดคล้องกับมาตรฐานคณิตศาสตร์สำหรับการสอนเรขาคณิตชั้น ม.1 แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูสามารถค้นหาสื่อการเรียนการสอนที่ตรงกับหลักสูตรและระดับความสามารถของนักเรียนได้อย่างรวดเร็ว ในขณะที่เครื่องมือปรับระดับความยากง่ายในตัว ช่วยให้สามารถปรับระดับความยากและความซับซ้อนของเนื้อหาได้อย่างราบรื่น แหล่งข้อมูลอเนกประสงค์เหล่านี้มีให้เลือกทั้งแบบพิมพ์ได้และแบบดิจิทัล รวมถึงไฟล์ PDF ที่ดาวน์โหลดได้ ทำให้ครูผู้สอนมีความยืดหยุ่นในการปรับการสอนให้เข้ากับสภาพแวดล้อมการเรียนรู้และความต้องการของนักเรียนที่หลากหลาย ไม่ว่าจะใช้สำหรับการแนะนำทักษะเบื้องต้น การแก้ไขปัญหาเฉพาะจุด การเสริมสร้างความรู้ขั้นสูง หรือการฝึกฝนอย่างสม่ำเสมอ แบบฝึกหัดการจำแนกมุมเหล่านี้สนับสนุนการวางแผนบทเรียนอย่างครอบคลุม และช่วยให้มั่นใจได้ว่านักเรียนจะพัฒนาความสามารถในการให้เหตุผลทางเรขาคณิตที่แข็งแกร่ง ซึ่งจำเป็นสำหรับหลักสูตรคณิตศาสตร์ขั้นสูง
