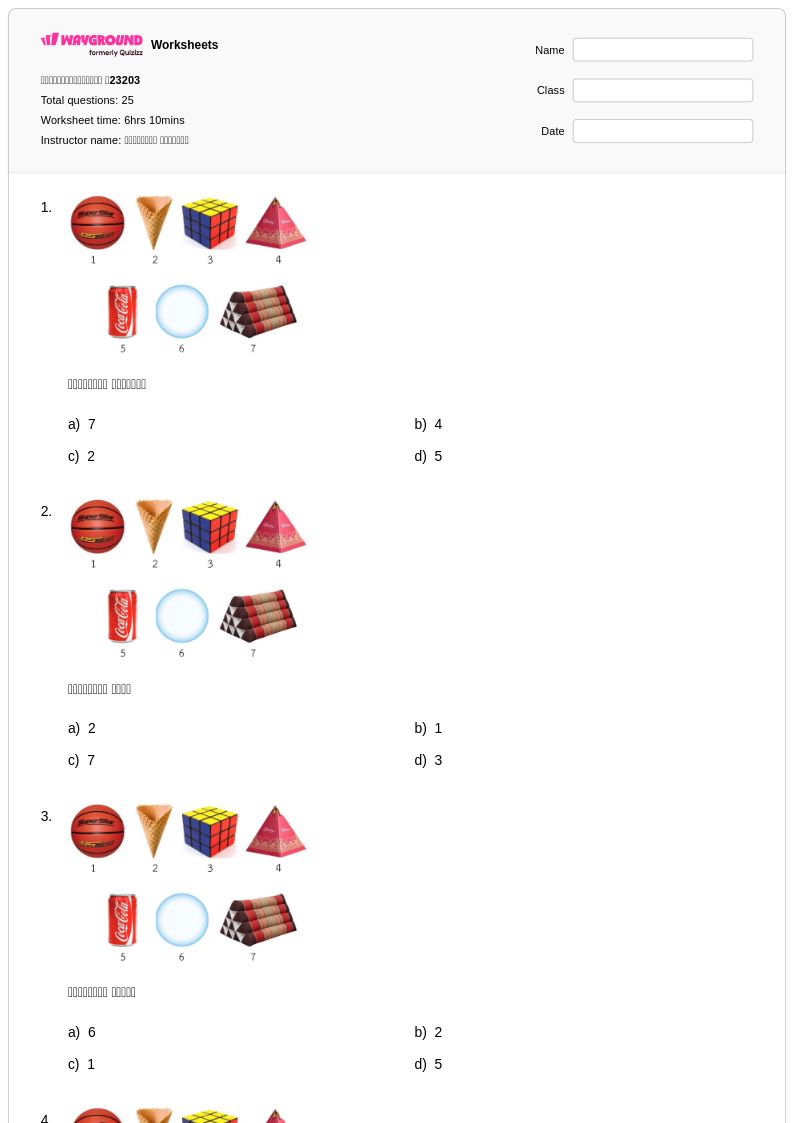
25 คิว
3rd

22 คิว
3rd

15 คิว
1st - 3rd

16 คิว
3rd
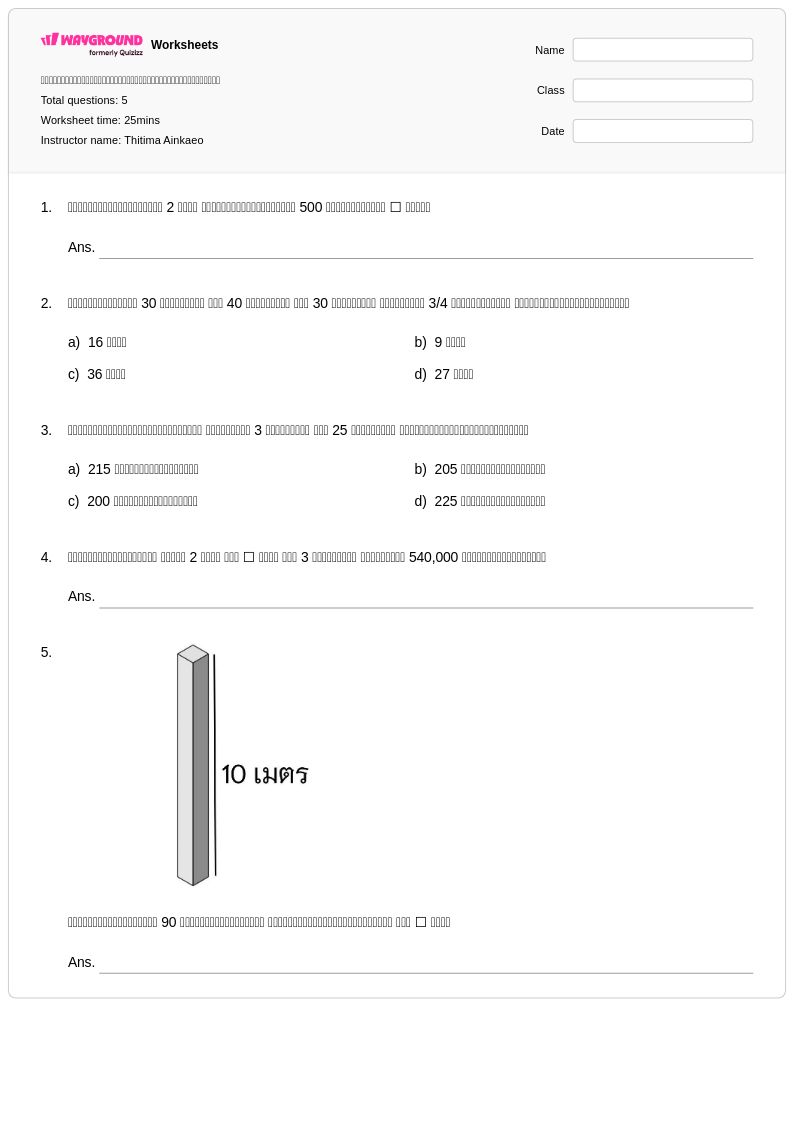
5 คิว
1st - 5th

10 คิว
3rd
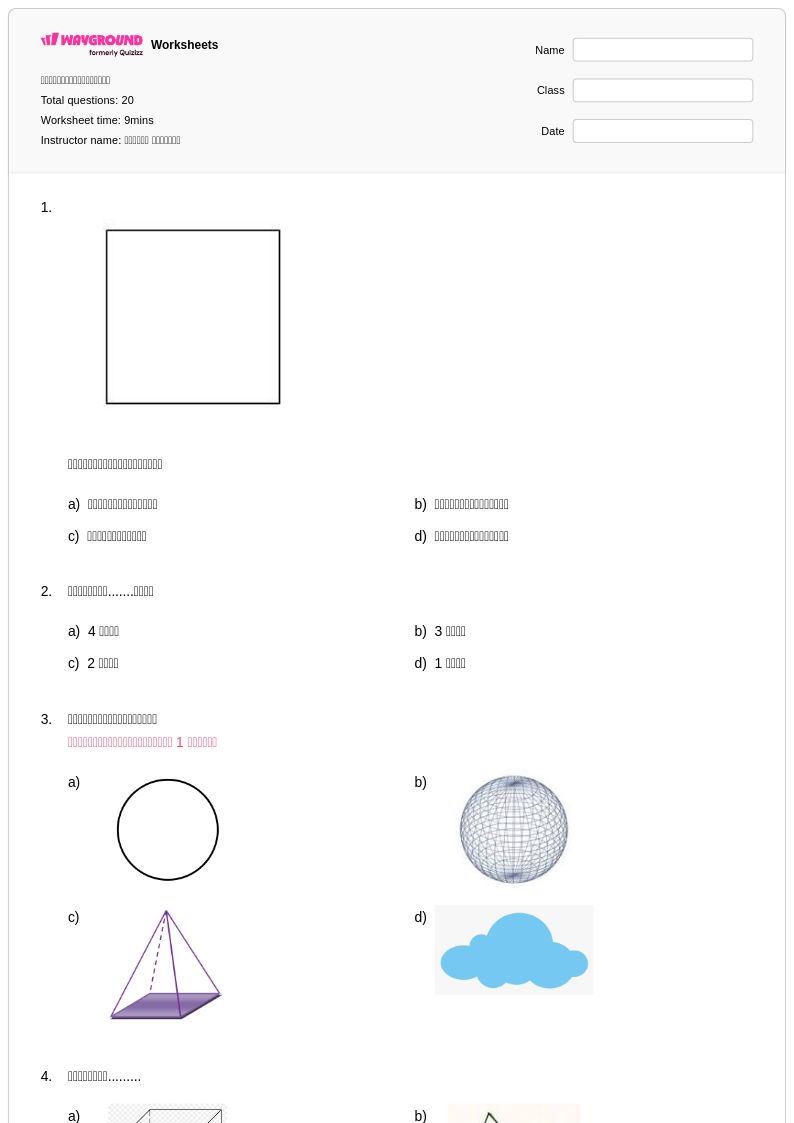
20 คิว
3rd - 12th

20 คิว
1st - 5th

10 คิว
3rd

8 คิว
3rd
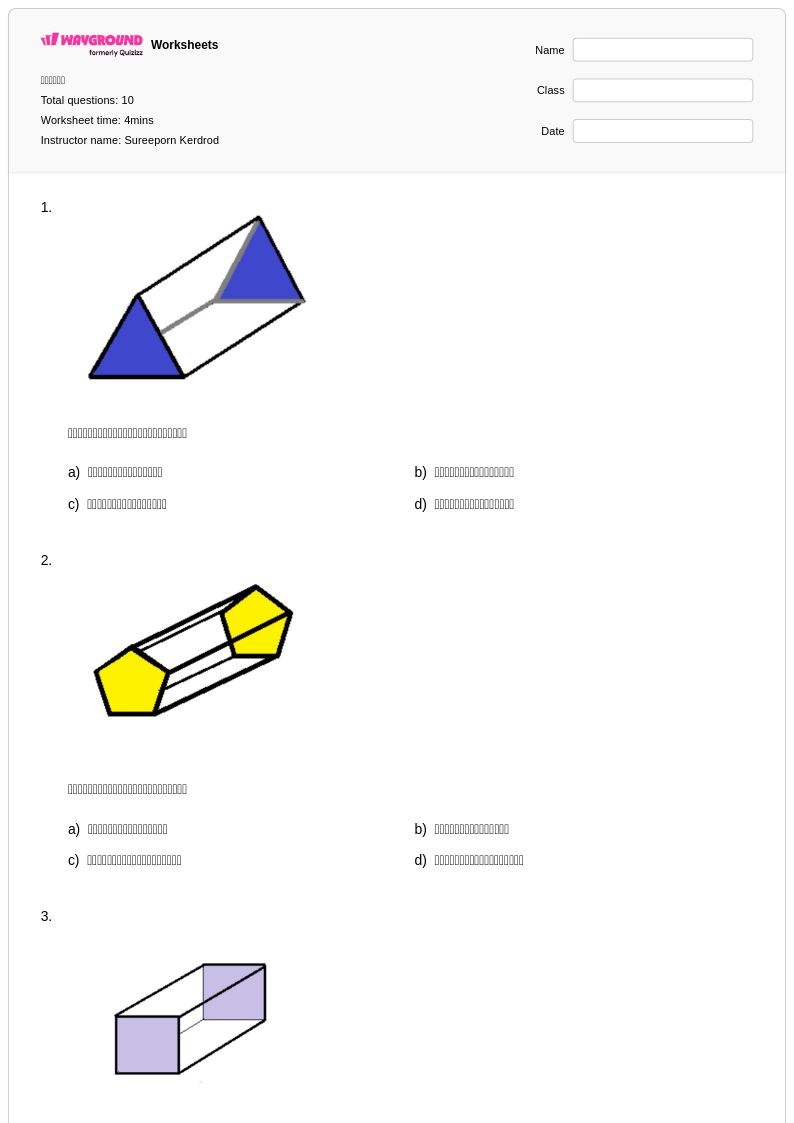
10 คิว
3rd - 6th

10 คิว
3rd

10 คิว
2nd - 4th
10 คิว
1st - 5th

32 คิว
1st - 5th

10 คิว
1st - 5th

10 คิว
1st - 3rd

18 คิว
1st - 5th

15 คิว
1st - Uni

40 คิว
3rd
11 คิว
3rd

7 คิว
1st - 5th

23 คิว
3rd

20 คิว
3rd - Uni
สำรวจแผ่นงาน ลูกบาศก์ ตามเกรด
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 3
สำรวจแผ่นงาน ลูกบาศก์ ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 3
แบบฝึกหัดลูกบาศก์สำหรับนักเรียนชั้นประถมศึกษาปีที่ 3 จาก Wayground (เดิมชื่อ Quizizz) เป็นแบบฝึกหัดพื้นฐานที่สำคัญสำหรับการเรียนรู้รูปทรงเรขาคณิตสามมิติ แบบฝึกหัดเหล่านี้เน้นเฉพาะการช่วยให้นักเรียนระบุ อธิบาย และวิเคราะห์คุณสมบัติของลูกบาศก์ผ่านแบบฝึกหัดภาพและกิจกรรมภาคปฏิบัติที่น่าสนใจ นักเรียนจะได้พัฒนาทักษะการคิดเชิงพื้นที่ที่สำคัญขณะทำแบบฝึกหัดที่ครอบคลุมลักษณะของลูกบาศก์ เช่น หน้า ขอบ และจุดยอด พร้อมทั้งสำรวจตัวอย่างวัตถุทรงลูกบาศก์ในโลกแห่งความเป็นจริง แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียดและไฟล์ PDF ให้ดาวน์โหลดฟรี ทำให้ครูผู้สอนสามารถนำไปใช้ในการสอนเรขาคณิตอย่างเป็นระบบ ซึ่งช่วยสร้างความมั่นใจในการจดจำรูปทรงสามมิติและการพัฒนาคำศัพท์ทางคณิตศาสตร์
Wayground (เดิมชื่อ Quizizz) สนับสนุนครูผู้สอนด้วยคลังแบบฝึกหัดลูกบาศก์ที่สร้างโดยครูผู้สอนหลายล้านชุด ซึ่งออกแบบมาโดยเฉพาะสำหรับการสอนคณิตศาสตร์ชั้นประถมศึกษาปีที่ 3 ความสามารถในการค้นหาและกรองข้อมูลที่แข็งแกร่งของแพลตฟอร์มช่วยให้ครูผู้สอนสามารถค้นหาแหล่งข้อมูลที่สอดคล้องกับมาตรฐานหลักสูตรและตรงกับความต้องการการเรียนรู้เฉพาะของนักเรียนได้อย่างรวดเร็ว ครูสามารถปรับการสอนให้เหมาะสมกับผู้เรียนแต่ละคนได้อย่างง่ายดาย โดยเลือกจากระดับความยากและรูปแบบแบบฝึกหัดที่หลากหลาย ในขณะที่เครื่องมือปรับแต่งที่ยืดหยุ่นช่วยให้สามารถปรับเปลี่ยนเพื่อให้เหมาะสมกับผู้เรียนที่หลากหลายได้ดียิ่งขึ้นในสถานการณ์การแก้ไขปัญหาและการเสริมสร้างความรู้ สื่อการเรียนการสอนที่เน้นรูปทรงเรขาคณิตสามมิตินี้มีให้เลือกทั้งแบบพิมพ์ได้และแบบดิจิทัล รวมถึงไฟล์ PDF ที่ดาวน์โหลดได้ ทำให้ครูผู้สอนมีความยืดหยุ่นในการบูรณาการการฝึกฝนเรขาคณิตสามมิติเข้ากับการวางแผนบทเรียน การบ้าน และกิจกรรมเสริมสร้างทักษะที่มุ่งเน้นการเสริมสร้างความเข้าใจเชิงพื้นที่และการให้เหตุผลทางเรขาคณิตได้อย่างราบรื่น
