
22 คิว
2nd

24 คิว
2nd
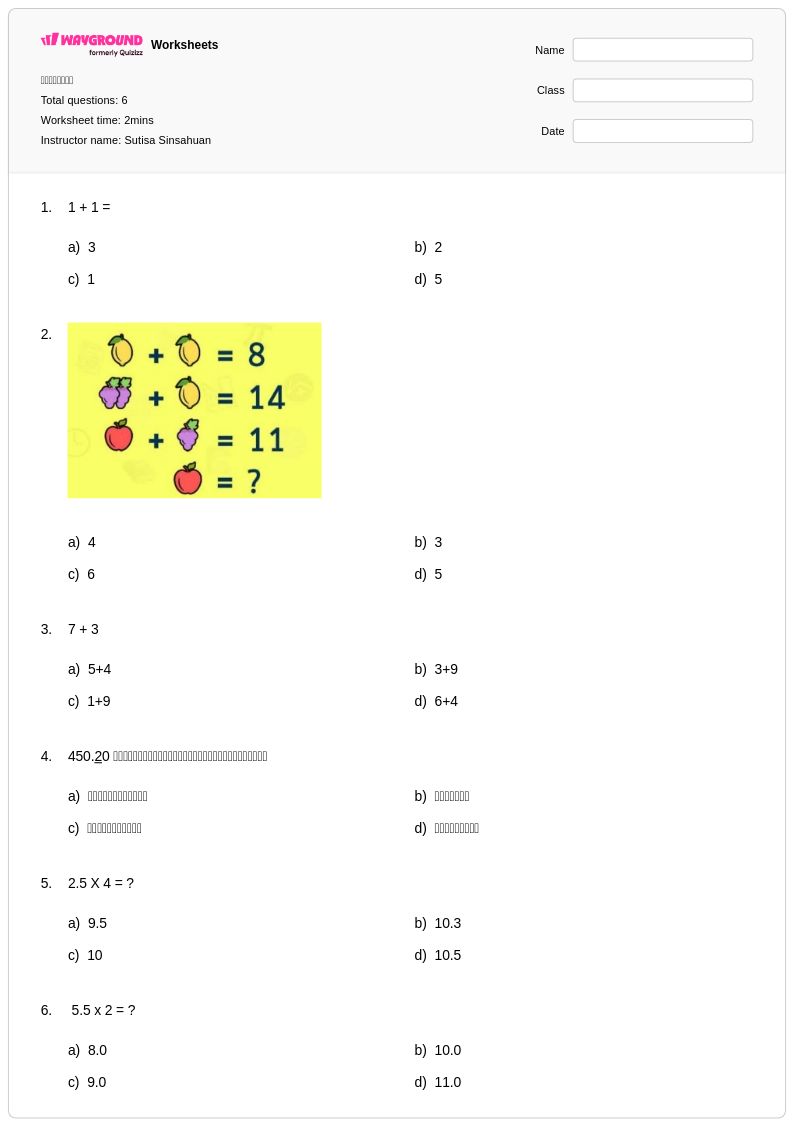
6 คิว
2nd - 6th
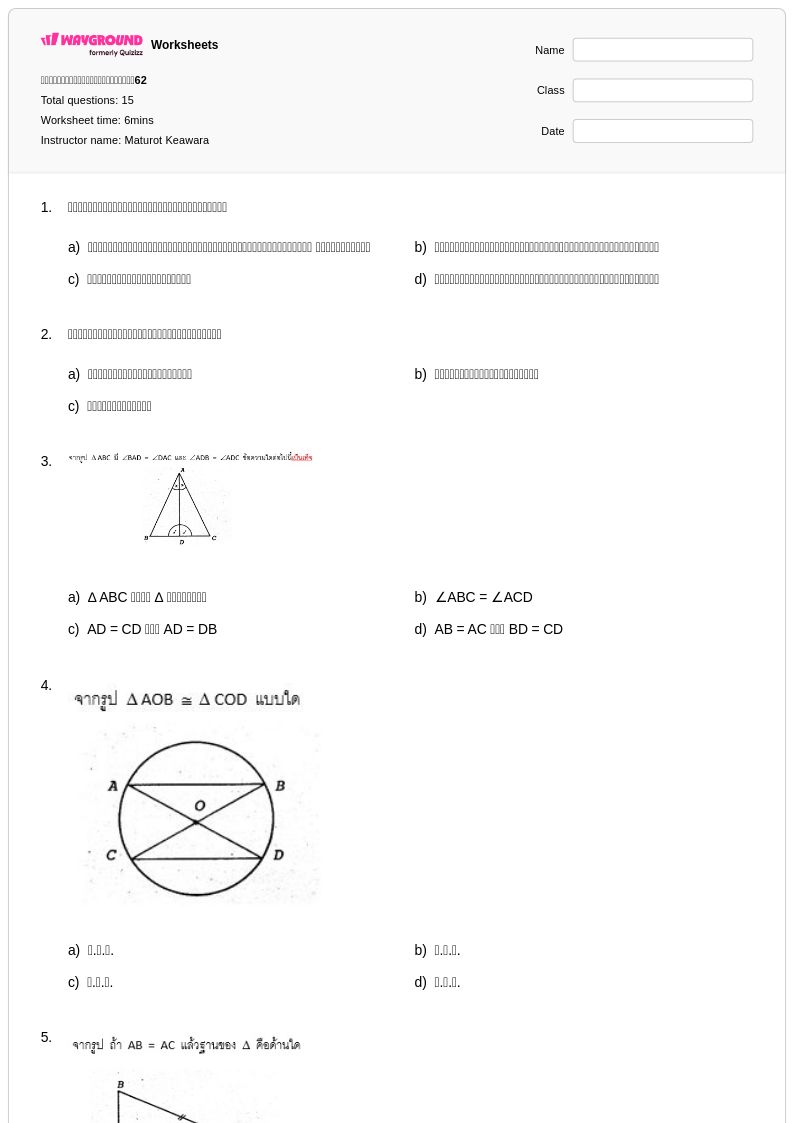
15 คิว
1st - 5th
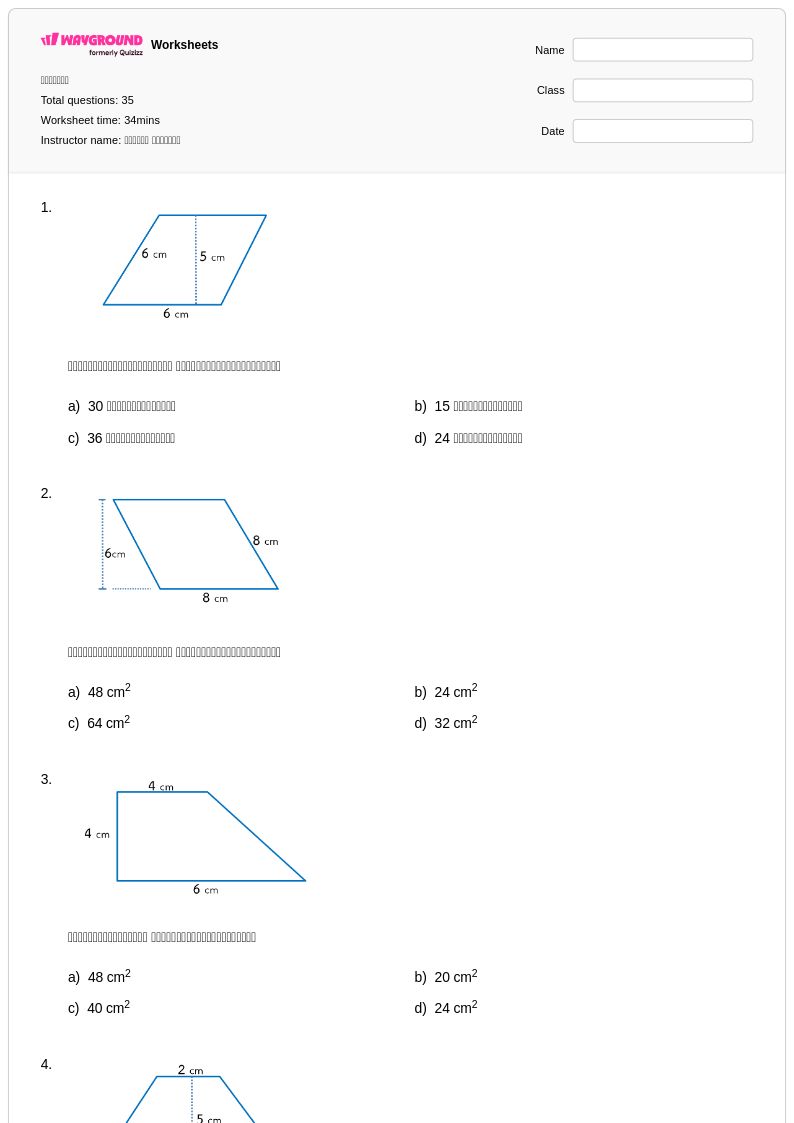
35 คิว
1st - 6th

30 คิว
2nd - 11th

10 คิว
2nd

20 คิว
1st - 5th
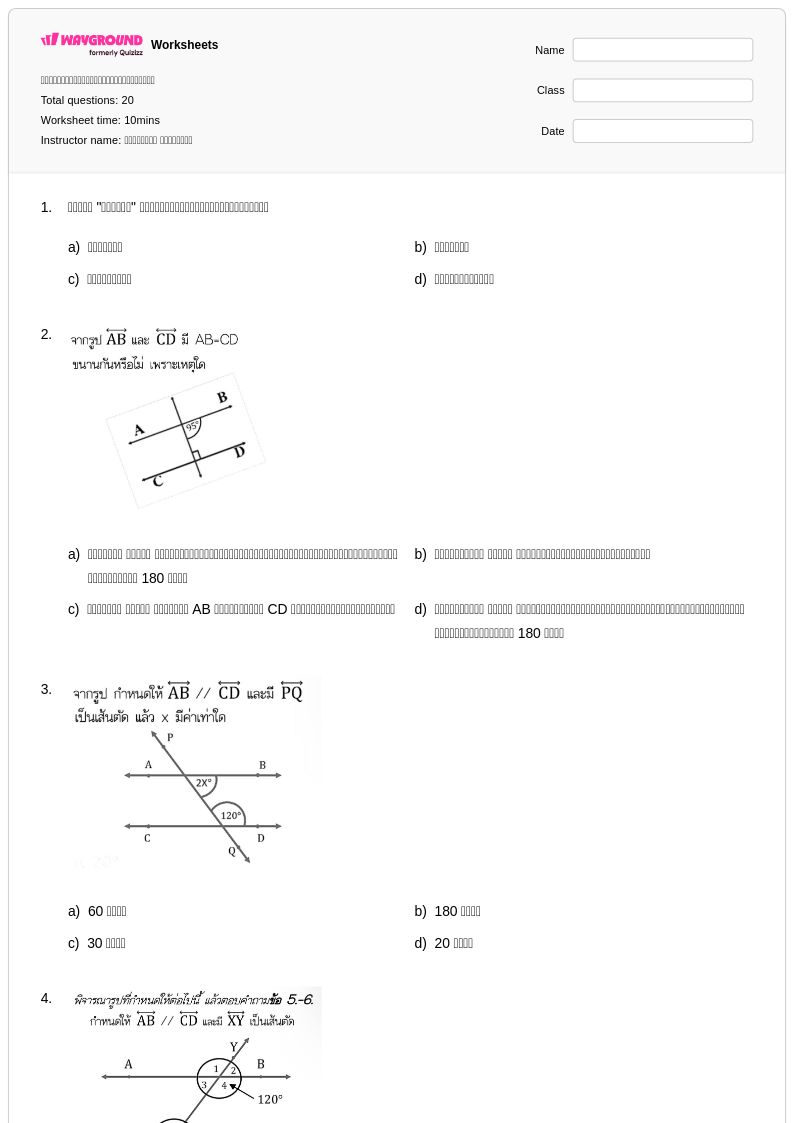
20 คิว
2nd
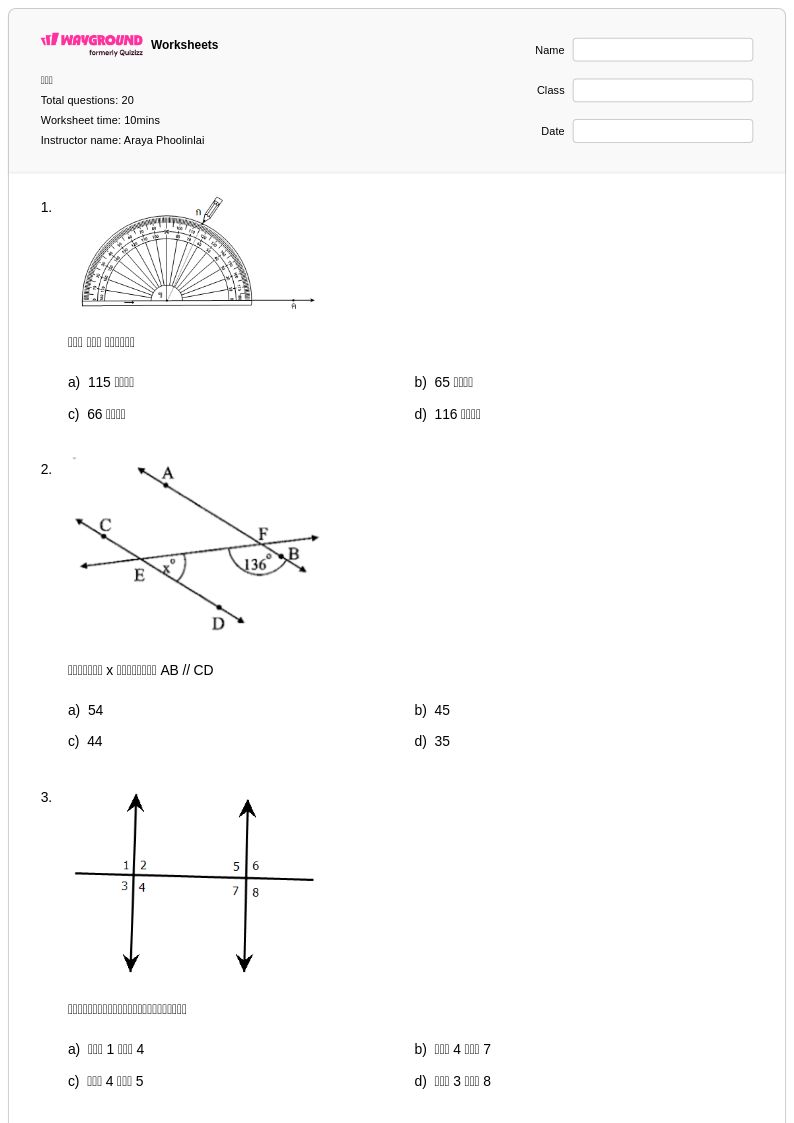
20 คิว
1st - 2nd

11 คิว
2nd - 4th
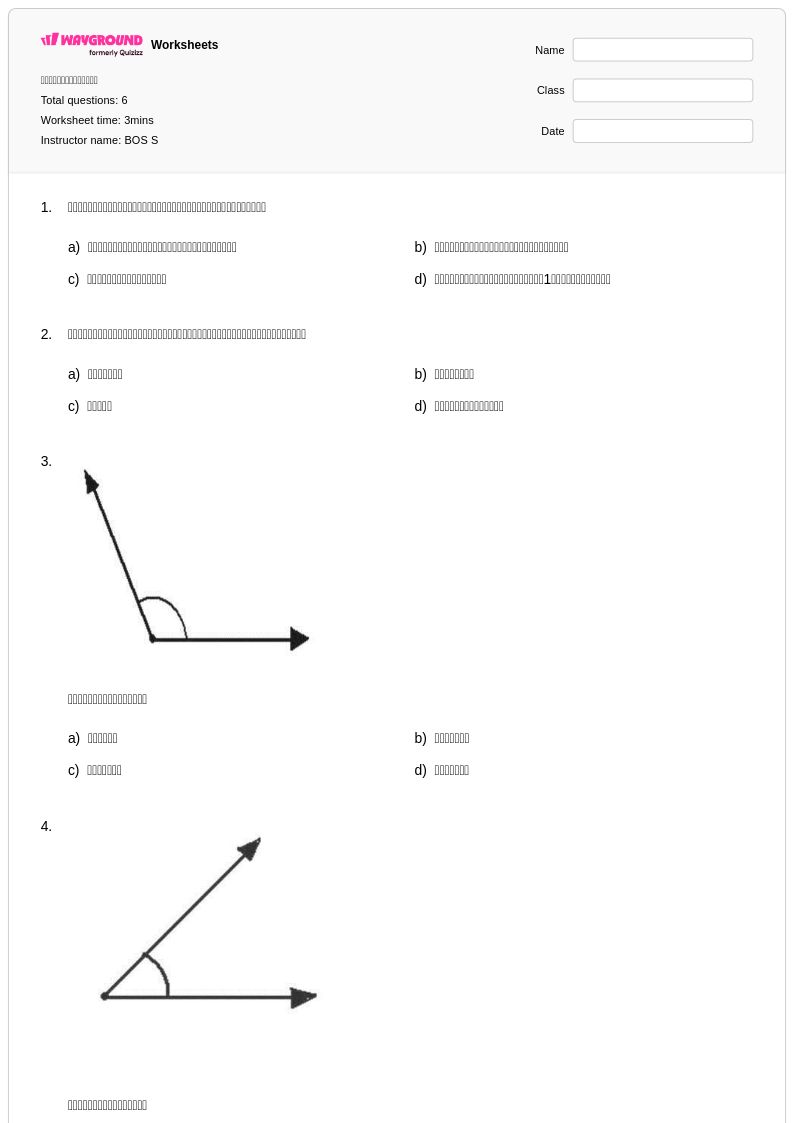
6 คิว
1st - Uni
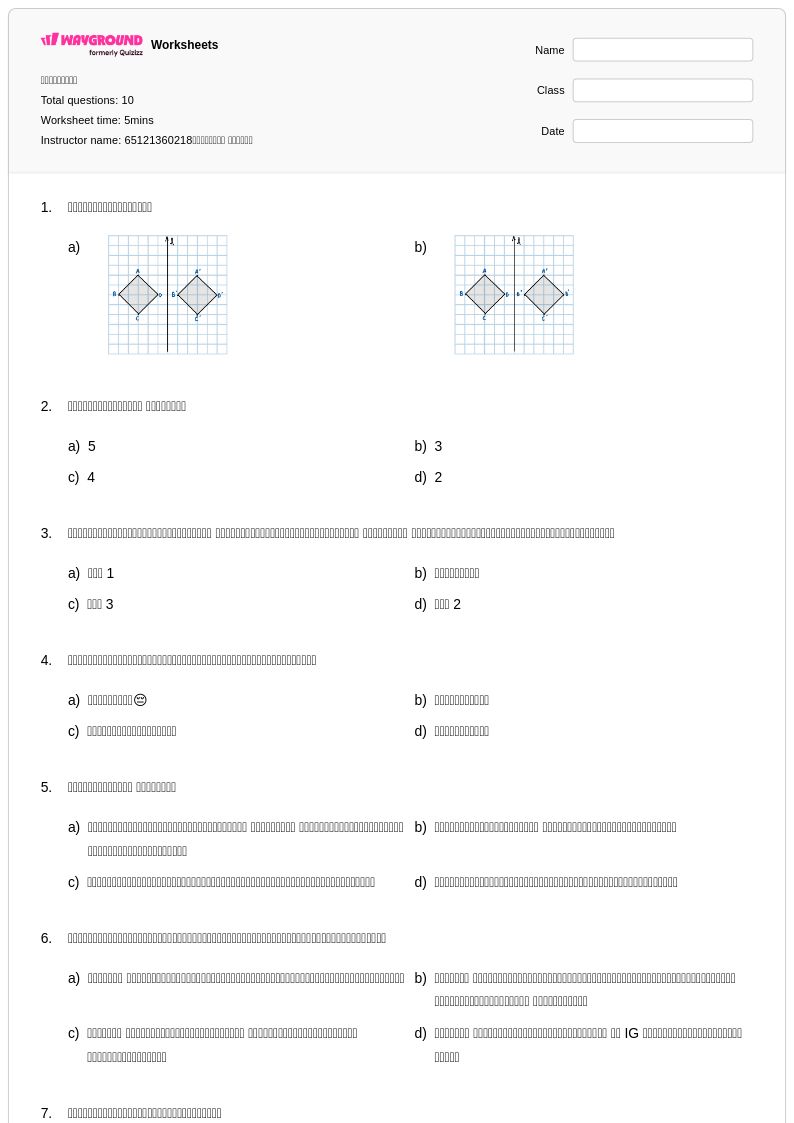
10 คิว
2nd

85 คิว
1st - 3rd
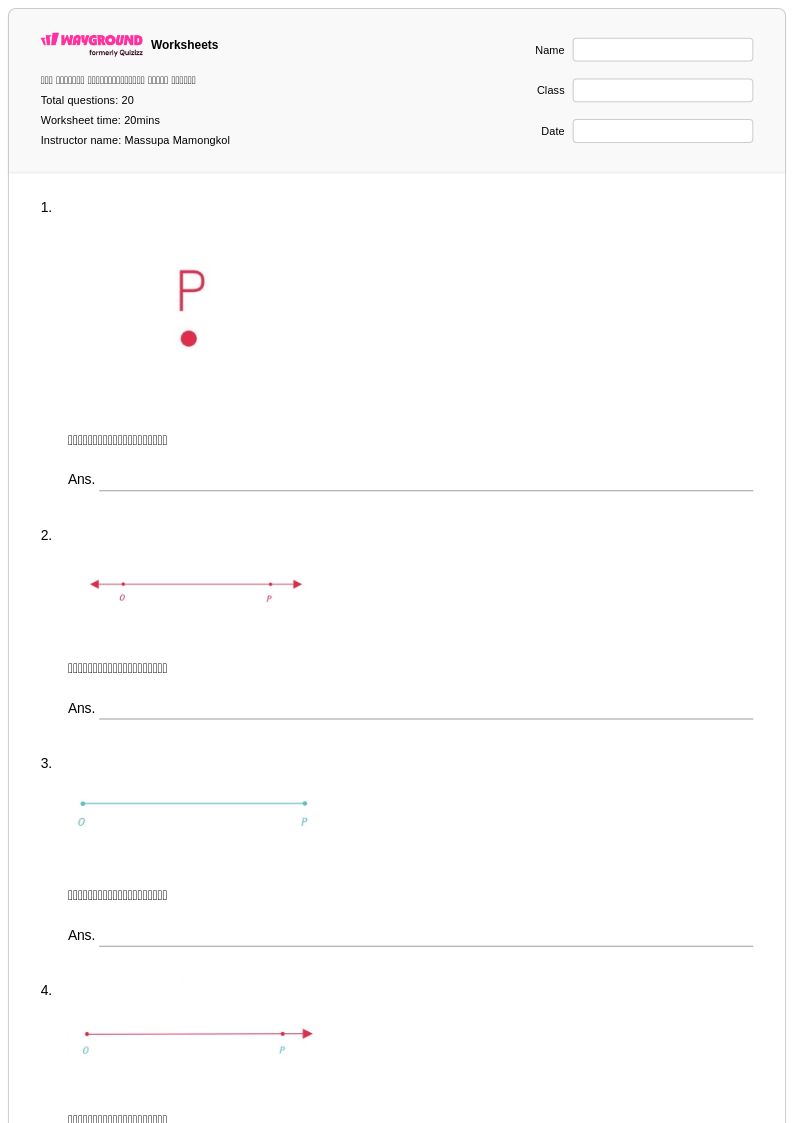
20 คิว
1st - 5th
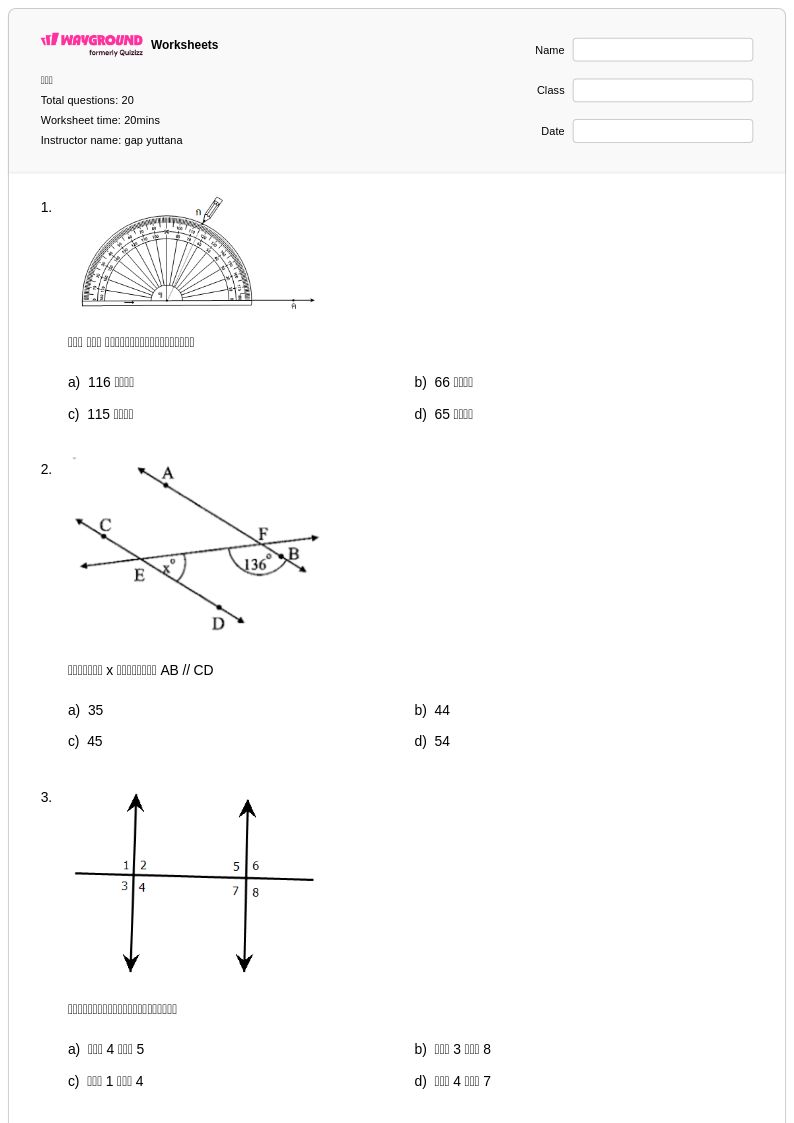
20 คิว
1st - 2nd

9 คิว
2nd
10 คิว
1st - 5th
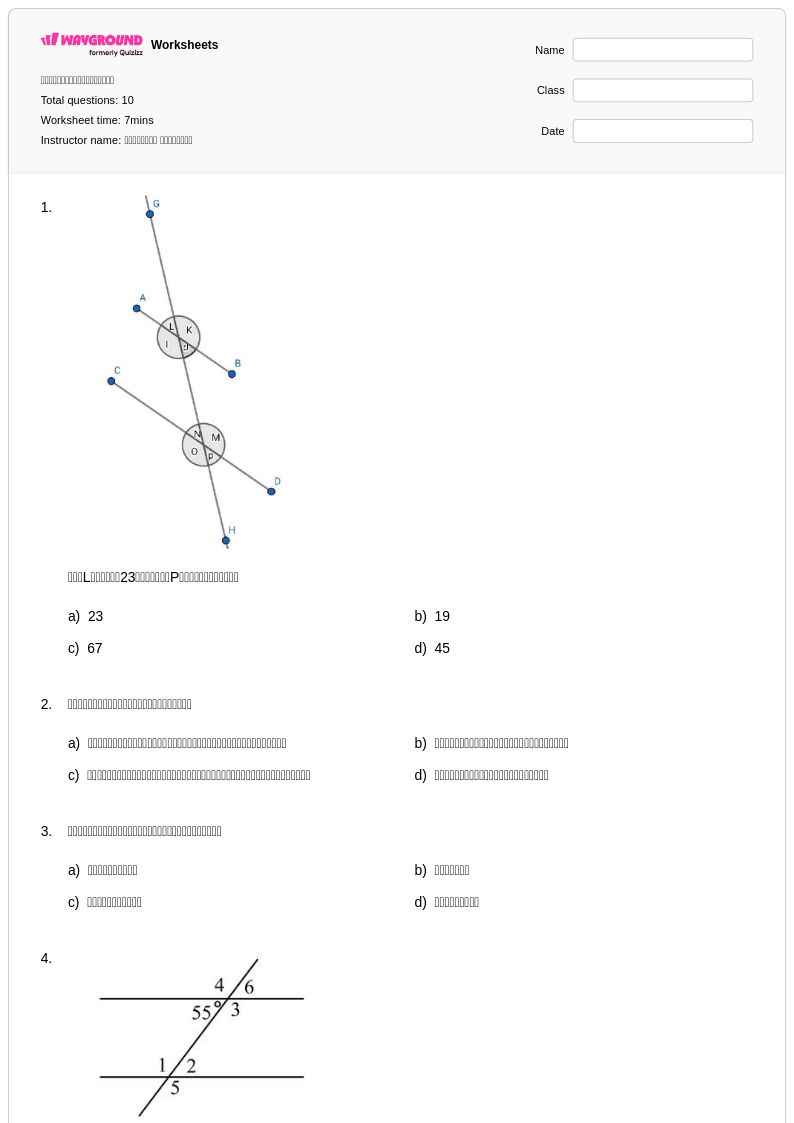
10 คิว
2nd
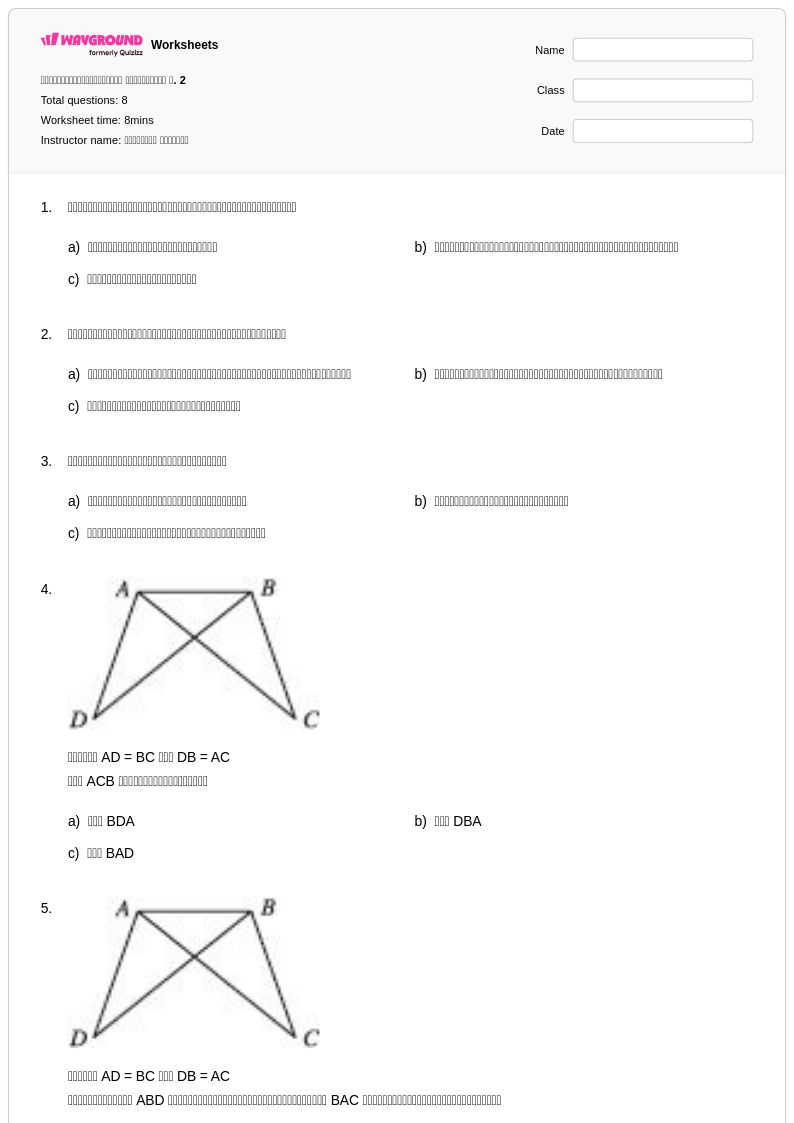
8 คิว
2nd
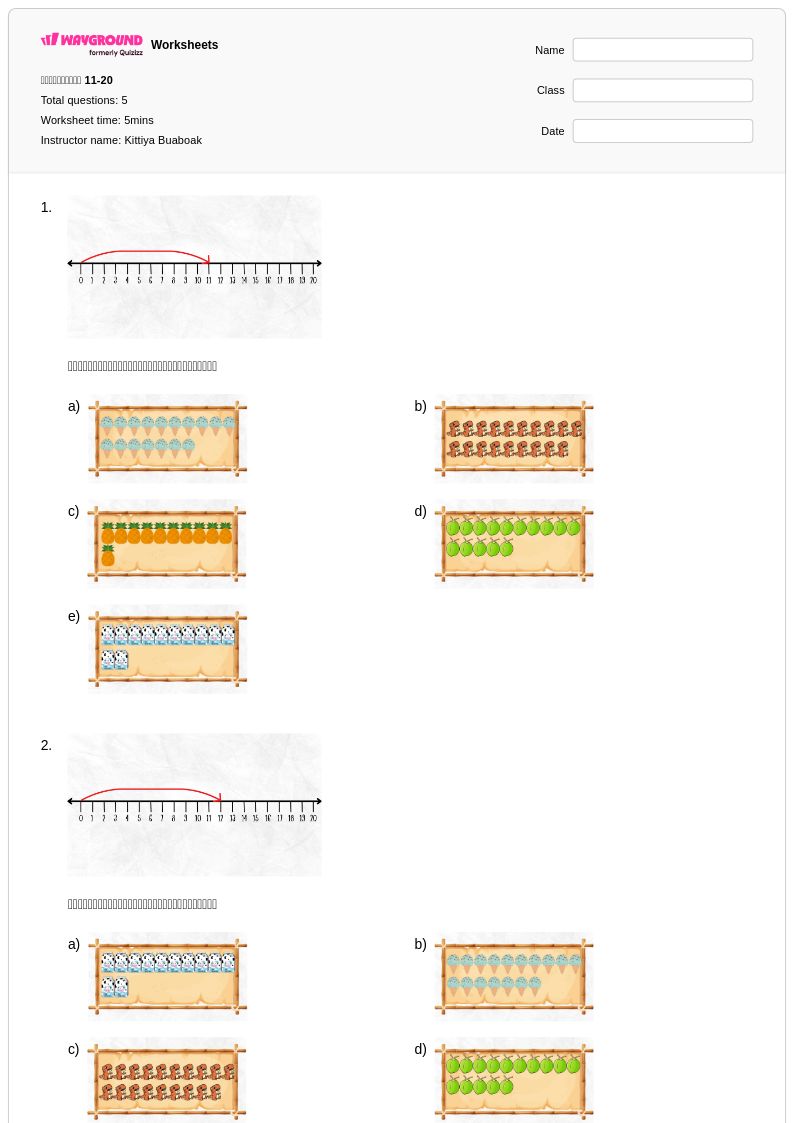
5 คิว
1st - 6th
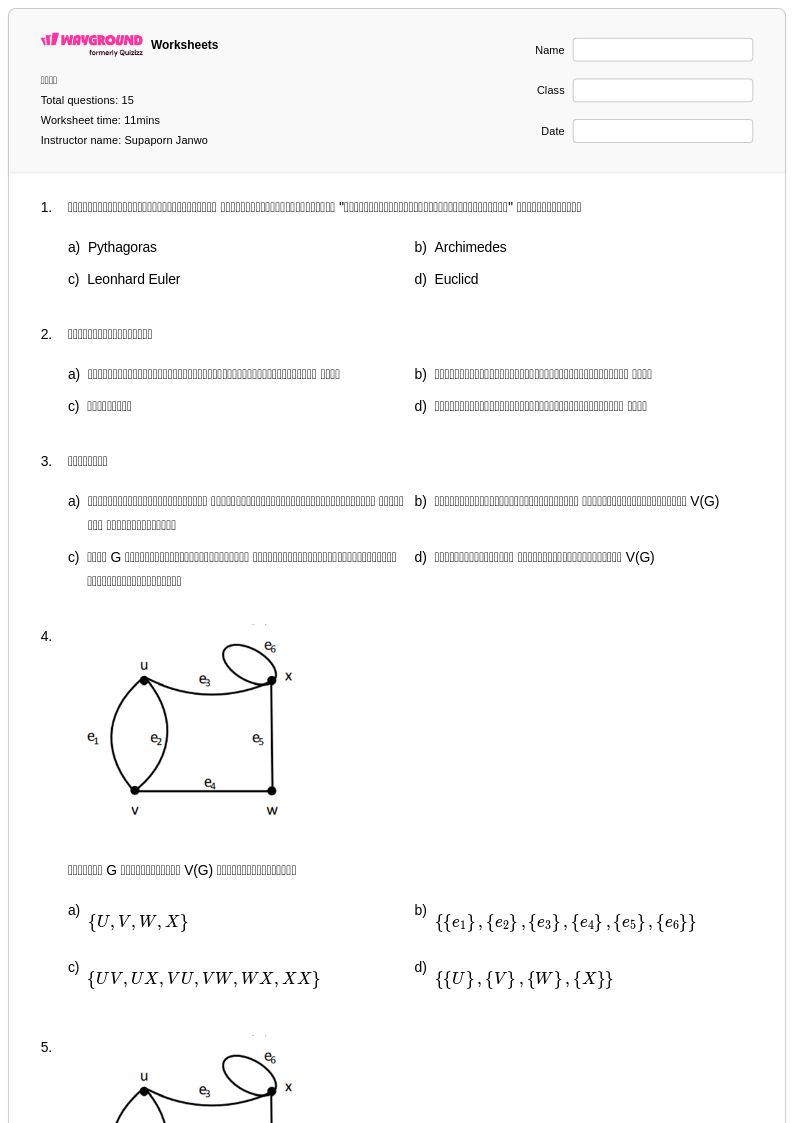
15 คิว
1st - 3rd

12 คิว
2nd

20 คิว
2nd
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 2
สำรวจแผ่นงาน เส้น ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 2
แบบฝึกหัดเรื่องเส้นสำหรับนักเรียนชั้นประถมศึกษาปีที่ 2 จาก Wayground (เดิมชื่อ Quizizz) เป็นแบบฝึกหัดเรขาคณิตพื้นฐานที่สำคัญ ช่วยแนะนำแนวคิดพื้นฐานที่สุดอย่างหนึ่งในวิชาคณิตศาสตร์ให้แก่ผู้เรียนรุ่นเยาว์ แบบฝึกหัดเหล่านี้ได้รับการออกแบบอย่างพิถีพิถัน ช่วยให้นักเรียนชั้นประถมศึกษาปีที่ 2 สามารถระบุ วาด และเข้าใจเส้นประเภทต่างๆ รวมถึงเส้นตรง เส้นโค้ง และส่วนของเส้นตรง ผ่านแบบฝึกหัดภาพที่น่าสนใจและกิจกรรมภาคปฏิบัติ แบบฝึกหัดแต่ละชุดมุ่งเน้นการพัฒนาทักษะการคิดเชิงพื้นที่และคำศัพท์ทางเรขาคณิต พร้อมทั้งมีแบบฝึกหัดที่เป็นระบบ ช่วยสร้างความมั่นใจในการจดจำเส้นในทิศทางและบริบทต่างๆ ครูสามารถเข้าถึงเฉลยคำตอบและไฟล์ PDF ฟรีที่สนับสนุนการสอนอย่างเป็นระบบในแนวคิดเรขาคณิตเบื้องต้นที่สำคัญนี้ เพื่อให้แน่ใจว่านักเรียนพัฒนาทักษะการคิดเชิงพื้นที่และภาพที่แข็งแกร่ง ซึ่งจะเป็นรากฐานสำหรับการทำความเข้าใจเรขาคณิตขั้นสูงต่อไป
คลังแบบฝึกหัดของ Wayground มีแบบฝึกหัดเรื่องเส้นที่สร้างโดยครูหลายล้านชุด ซึ่งออกแบบมาโดยเฉพาะสำหรับการสอนคณิตศาสตร์ชั้นประถมศึกษาปีที่ 2 ช่วยให้ครูมีเครื่องมือค้นหาและกรองข้อมูลที่มีประสิทธิภาพ เพื่อค้นหาแหล่งข้อมูลที่ตรงกับความต้องการของห้องเรียนและมาตรฐานการเรียนการสอนได้อย่างสมบูรณ์แบบ เครื่องมือปรับระดับความยากง่ายของแพลตฟอร์มนี้ช่วยให้ครูสามารถปรับแต่งแบบฝึกหัดให้เหมาะกับรูปแบบการเรียนรู้และระดับความสามารถที่หลากหลาย ในขณะที่ตัวเลือกการจัดรูปแบบที่ยืดหยุ่นช่วยให้สามารถสร้างทั้งไฟล์ PDF ที่พิมพ์ได้สำหรับงานแบบดั้งเดิมที่ใช้กระดาษและดินสอ และรูปแบบดิจิทัลสำหรับประสบการณ์การเรียนรู้แบบโต้ตอบ ชุดแบบฝึกหัดที่ครอบคลุมเหล่านี้สนับสนุนการวางแผนบทเรียนที่มีประสิทธิภาพโดยนำเสนอวิธีการที่หลากหลายในการฝึกทักษะการจดจำเส้นและการวาดภาพ พร้อมทั้งมีแหล่งข้อมูลที่ตรงเป้าหมายสำหรับการแก้ไขปัญหาเมื่อนักเรียนต้องการการสนับสนุนเพิ่มเติม และโอกาสในการเสริมสร้างความรู้สำหรับผู้เรียนขั้นสูงที่พร้อมจะสำรวจความสัมพันธ์ทางเรขาคณิตที่ซับซ้อนมากขึ้นและแนวคิดเชิงพื้นที่
