
10Q
9th - 10th

10Q
9th - 10th

10Q
9th - 10th
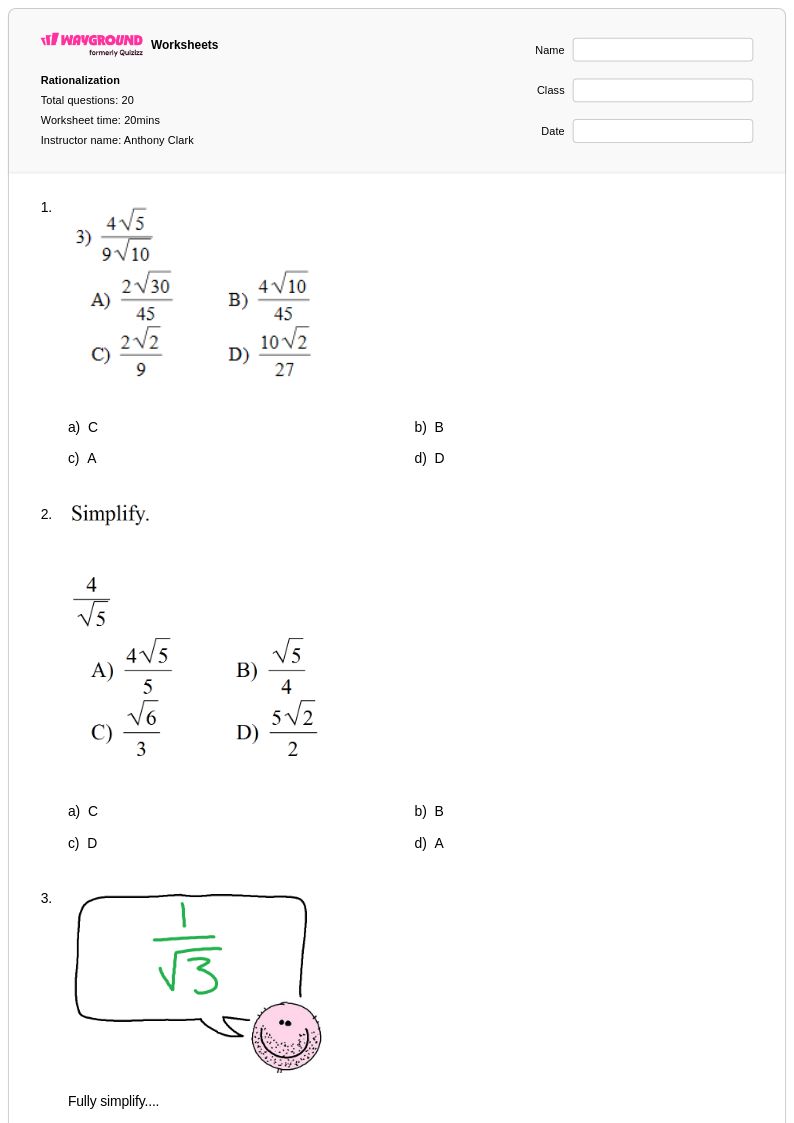
20Q
9th - Uni

5Q
9th

31Q
8th - 9th

16Q
9th - 12th

50Q
8th - 9th
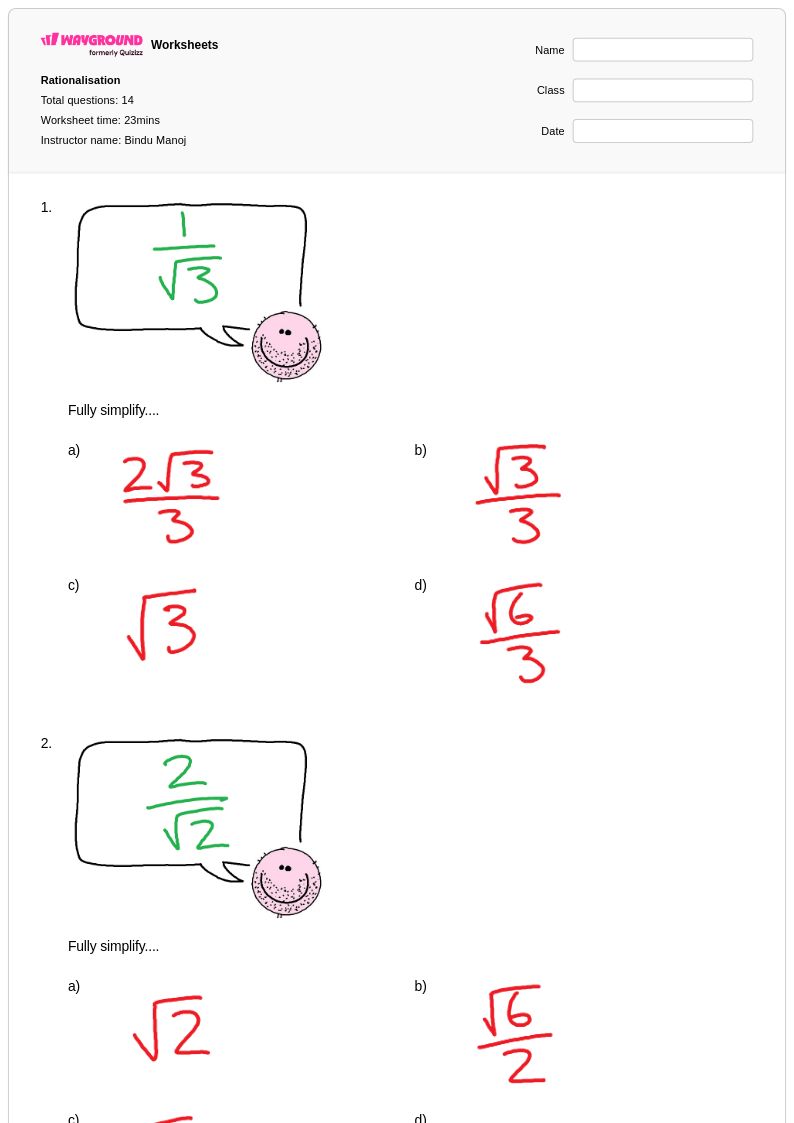
14Q
9th

20Q
9th

12Q
9th

8Q
7th - Uni
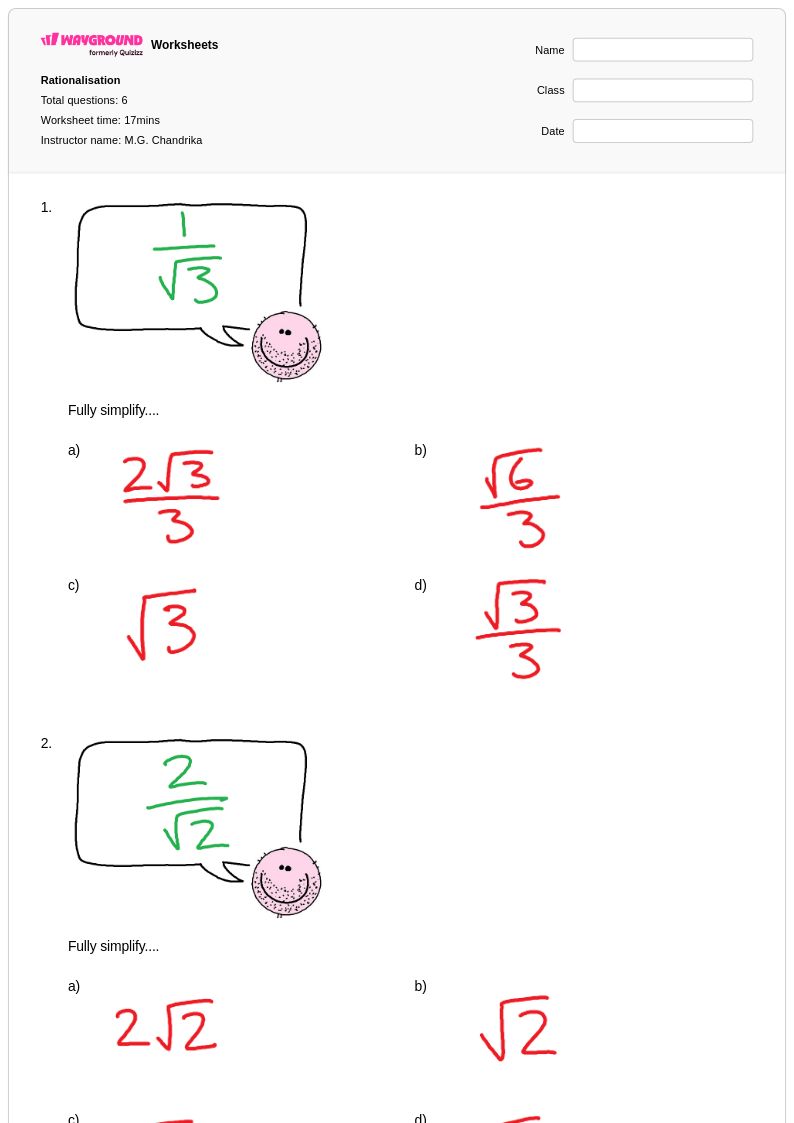
6Q
9th

12Q
9th - 12th

15Q
8th - 9th

20Q
9th - 12th

19Q
9th - 12th

20Q
9th

10Q
9th - 12th

38Q
9th - 12th

10Q
9th - 12th

9Q
9th - 12th
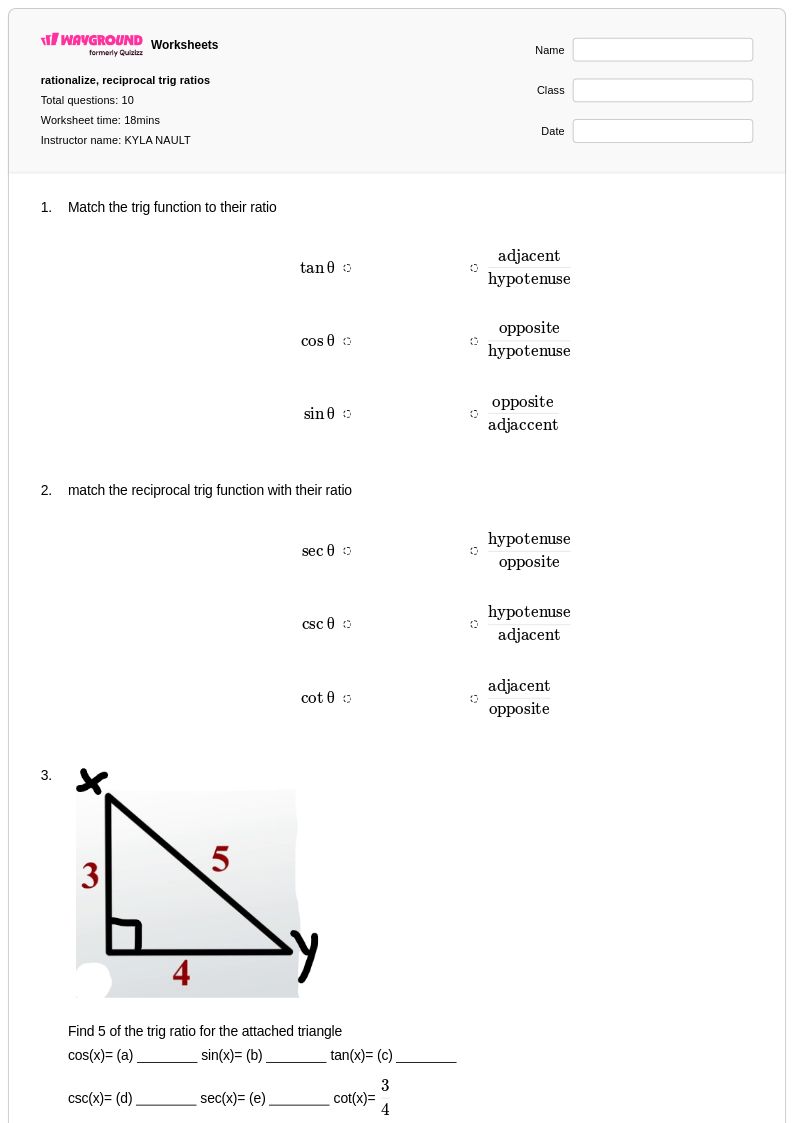
10Q
9th - 12th
11Q
8th - 11th
Explore otras hojas de trabajo de materias para ระดับ 9
สำรวจแผ่นงาน การปรับปรุงให้มีเหตุผล ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 9
แบบฝึกหัดการทำให้เป็นจำนวนตรรกยะสำหรับนักเรียนชั้น ม.3 จาก Wayground (เดิมชื่อ Quizizz) ให้แบบฝึกหัดที่ครอบคลุมเกี่ยวกับการกำจัดจำนวนอตรรกยะออกจากตัวส่วนและการทำให้พจน์พีชคณิตที่ซับซ้อนง่ายขึ้น แหล่งข้อมูลที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยให้นักเรียนเชี่ยวชาญเทคนิคที่สำคัญในการทำให้ตัวส่วนที่มีรากที่สอง รากที่สาม และนิพจน์รากอื่นๆ เป็นจำนวนตรรกยะ พร้อมทั้งพัฒนาความชำนาญในการจัดการกับตัวประกอบร่วมและการประยุกต์ใช้หลักการพีชคณิตพื้นฐาน แบบฝึกหัดแต่ละชุดประกอบด้วยโจทย์ฝึกหัดที่มีโครงสร้างซึ่งค่อยๆ พัฒนาจากโจทย์การทำให้เป็นจำนวนตรรกยะแบบพจน์เดียวพื้นฐานไปจนถึงโจทย์หลายขั้นตอนที่ซับซ้อนมากขึ้นซึ่งเกี่ยวข้องกับตัวส่วนทวินาม พร้อมเฉลยคำตอบเพื่อสนับสนุนการเรียนรู้ด้วยตนเอง นักเรียนจะได้รับความมั่นใจในการทำงานกับนิพจน์อตรรกยะผ่านแหล่งข้อมูลที่พิมพ์ได้ฟรีเหล่านี้ ซึ่งเสริมสร้างทักษะพีชคณิตที่สำคัญที่จำเป็นสำหรับหลักสูตรคณิตศาสตร์ขั้นสูงและการประเมินมาตรฐาน
คลังข้อมูลขนาดใหญ่ของ Wayground นำเสนอแบบฝึกหัดการให้เหตุผลเชิงตรรกะที่สร้างโดยนักการศึกษาหลายล้านชุด ซึ่งออกแบบมาโดยเฉพาะสำหรับการสอนคณิตศาสตร์ระดับชั้น ม.3 โดยมีฟังก์ชันการค้นหาและการกรองที่มีประสิทธิภาพ ช่วยให้ค้นหาแหล่งข้อมูลที่สอดคล้องกับมาตรฐานหลักสูตรและวัตถุประสงค์การเรียนรู้ได้อย่างรวดเร็ว ครูสามารถปรับแต่งสื่อเหล่านี้ให้เข้ากับความต้องการที่หลากหลายของห้องเรียนได้อย่างง่ายดาย โดยเลือกจากรูปแบบ PDF ที่พิมพ์ได้สำหรับงานมอบหมายแบบดั้งเดิม หรือเวอร์ชันดิจิทัลสำหรับประสบการณ์การเรียนรู้แบบโต้ตอบ เครื่องมือการปรับระดับความยากง่ายของแพลตฟอร์มช่วยให้ครูสามารถปรับเปลี่ยนระดับความยากและประเภทของปัญหา ทำให้ง่ายต่อการให้ความช่วยเหลือเฉพาะจุดแก่นักเรียนที่ประสบปัญหา หรือกิจกรรมเสริมสำหรับผู้เรียนที่มีความสามารถสูง ชุดแบบฝึกหัดที่ครอบคลุมนี้ช่วยลดความซับซ้อนในการวางแผนบทเรียน ในขณะเดียวกันก็รับประกันว่านักเรียนจะได้รับโอกาสในการฝึกฝนที่มีคุณภาพสูงอย่างสม่ำเสมอ ซึ่งจะช่วยเสริมสร้างเทคนิคการให้เหตุผลเชิงตรรกะที่ถูกต้อง และสร้างทักษะการให้เหตุผลทางคณิตศาสตร์ที่จำเป็นต่อความสำเร็จในหลักสูตรพีชคณิตระดับสูง
