
15Q
2nd - Uni

20Q
2nd - Uni

10Q
2nd - Uni
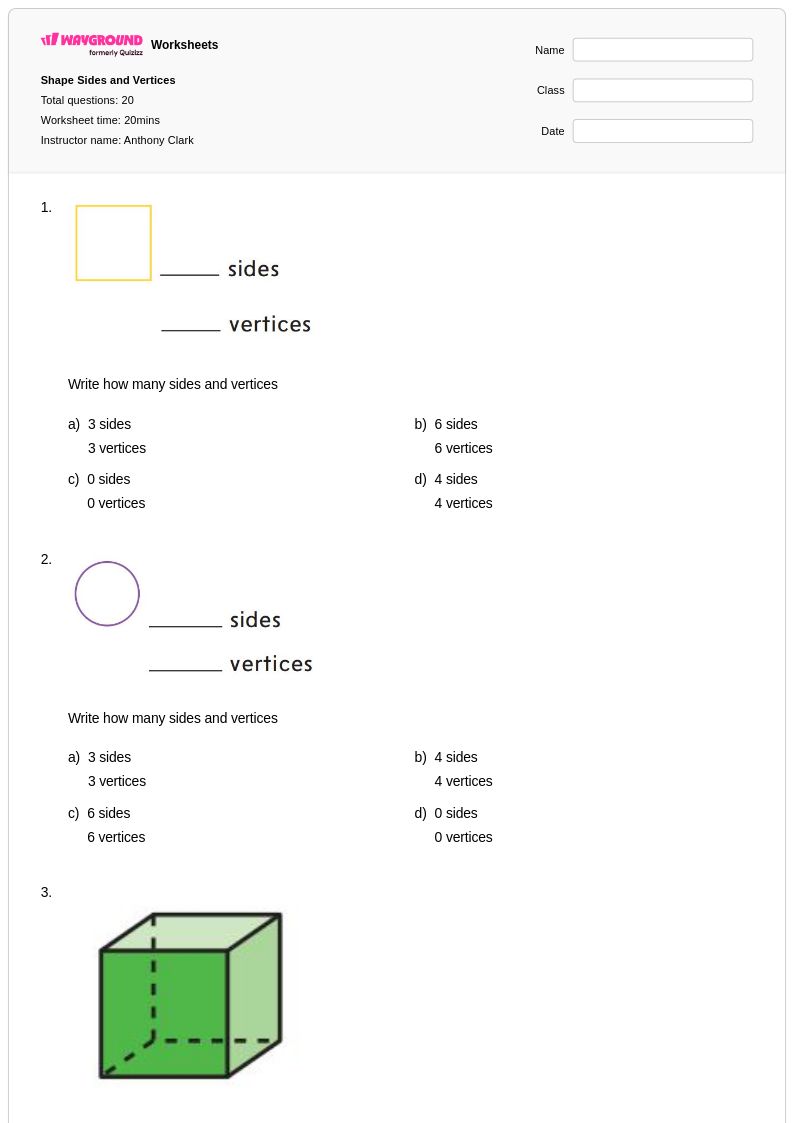
20Q
2nd - Uni

15Q
3rd - Uni

20Q
2nd - Uni

20Q
2nd - Uni

10Q
2nd - Uni

15Q
2nd - Uni

15Q
2nd - Uni

18Q
3rd
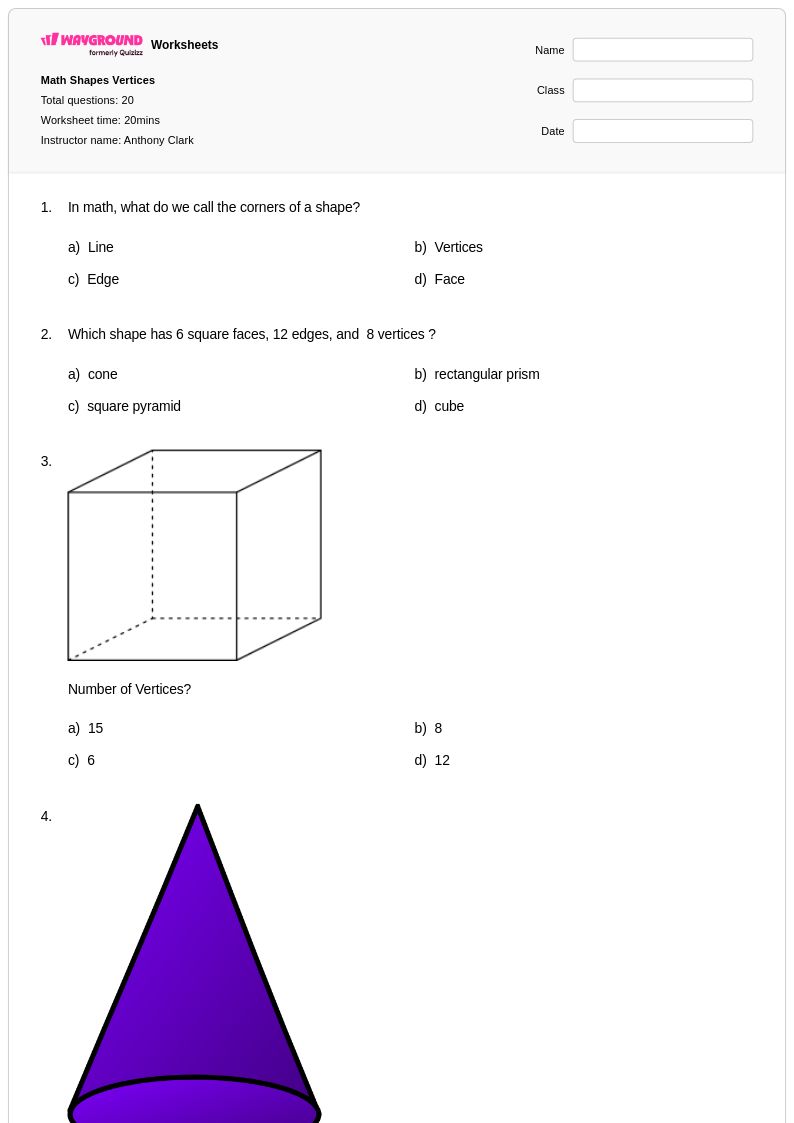
20Q
3rd - Uni

15Q
3rd
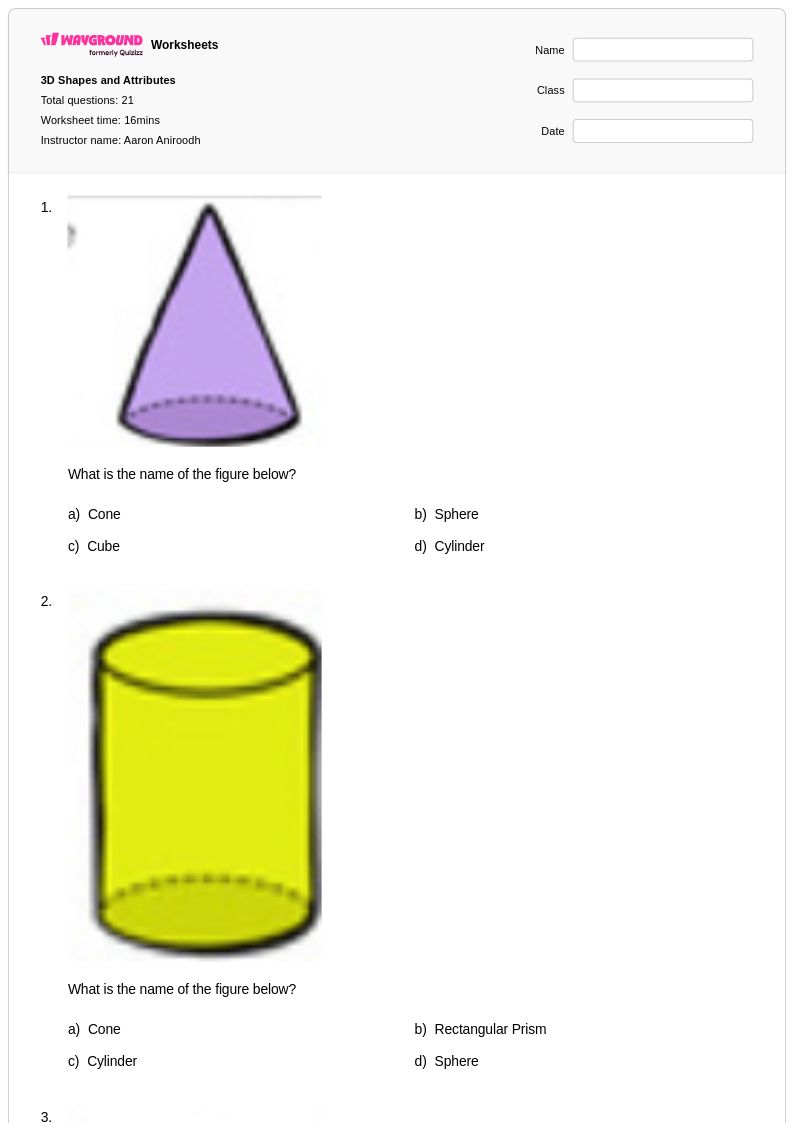
21Q
3rd
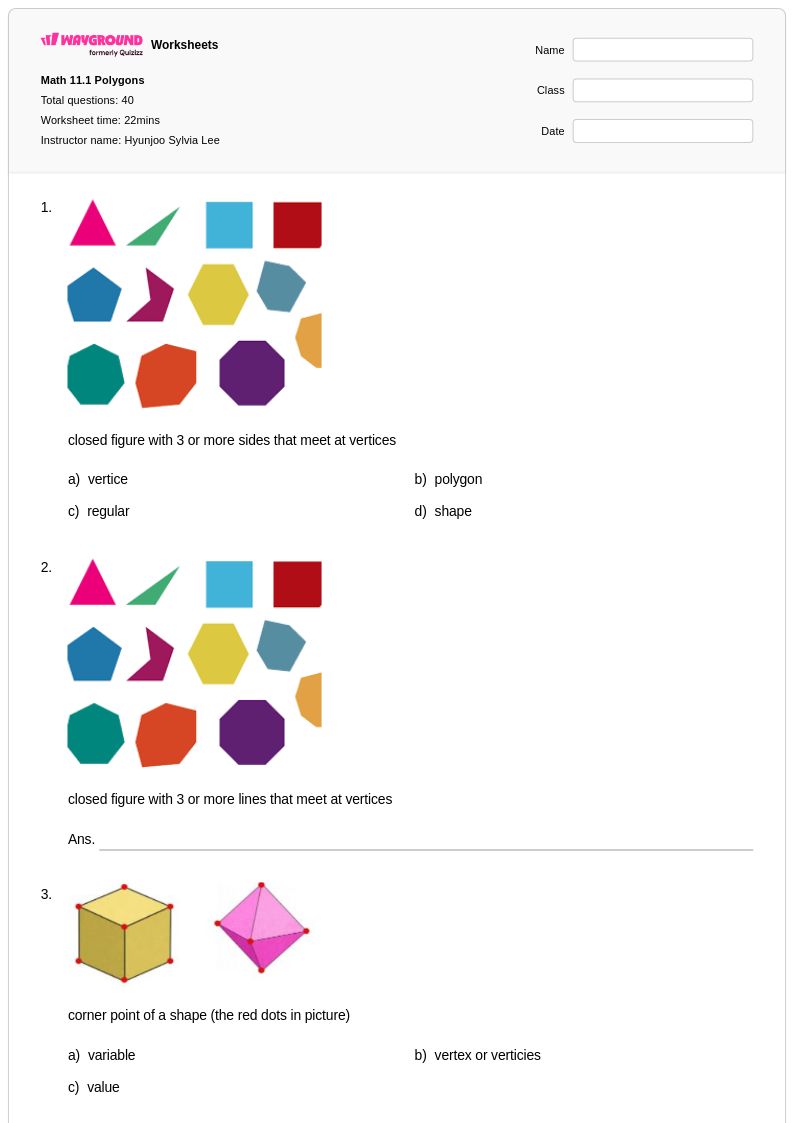
40Q
3rd - 5th
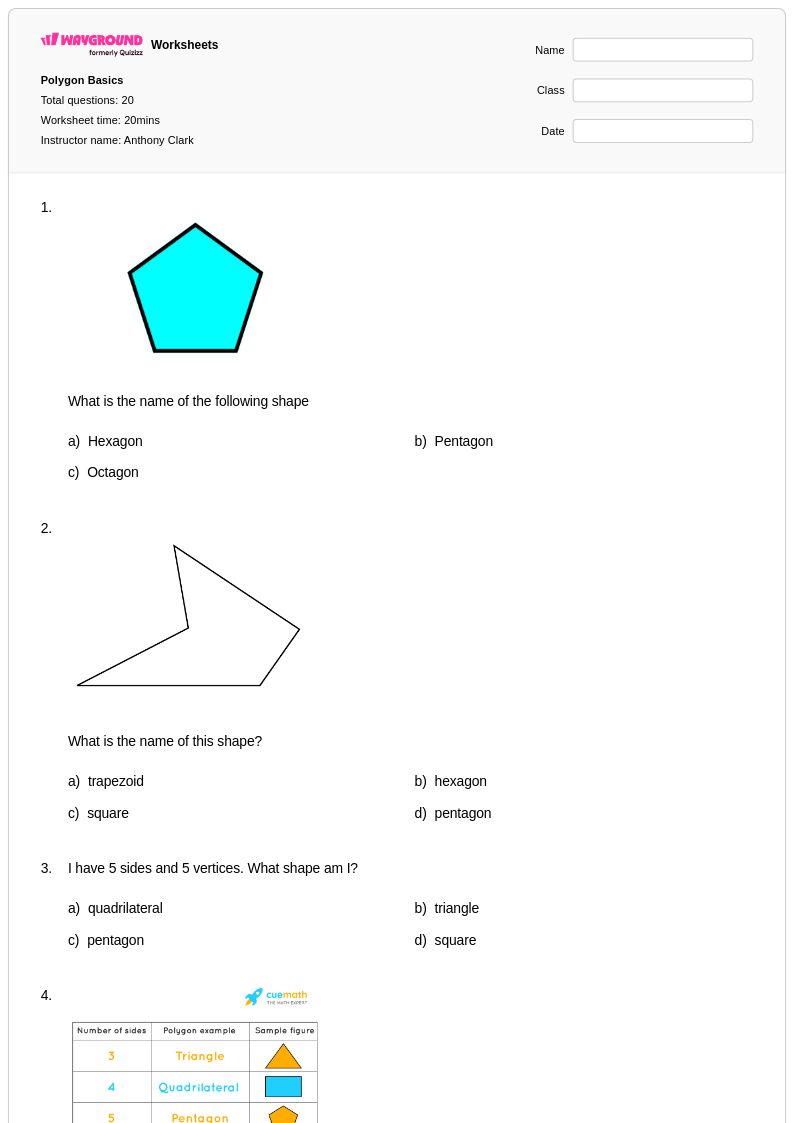
20Q
3rd - Uni
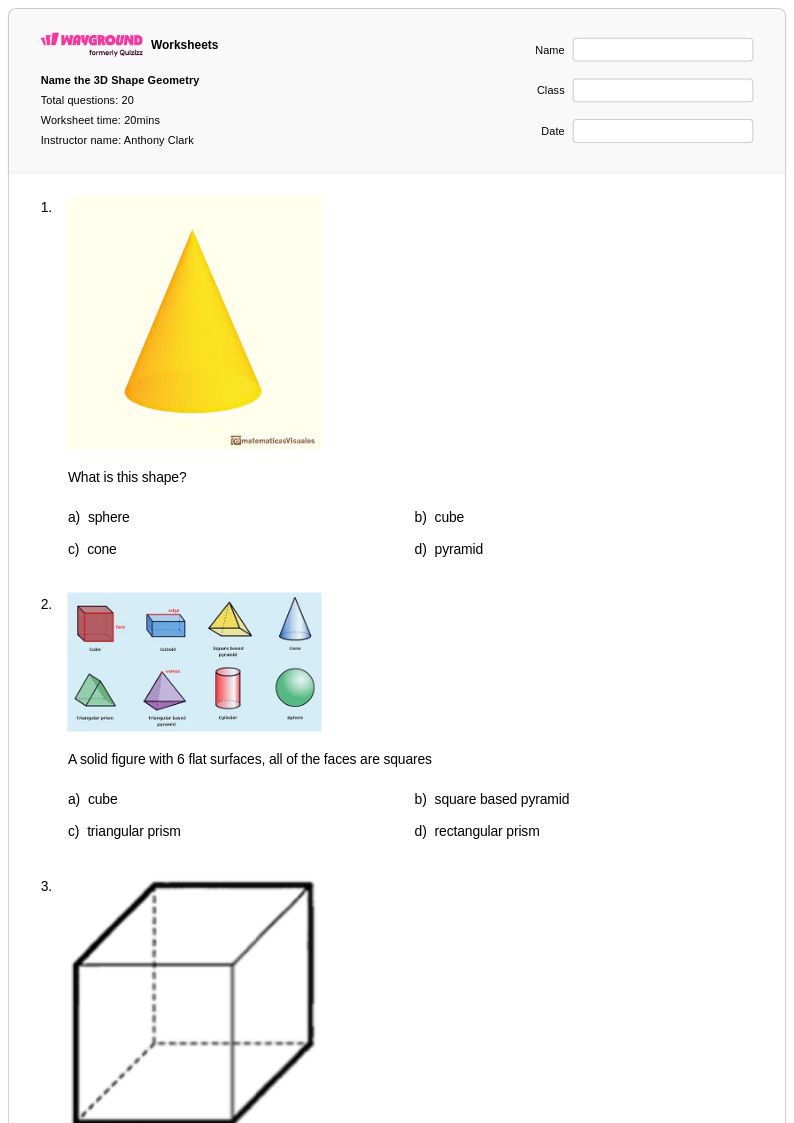
20Q
2nd - Uni
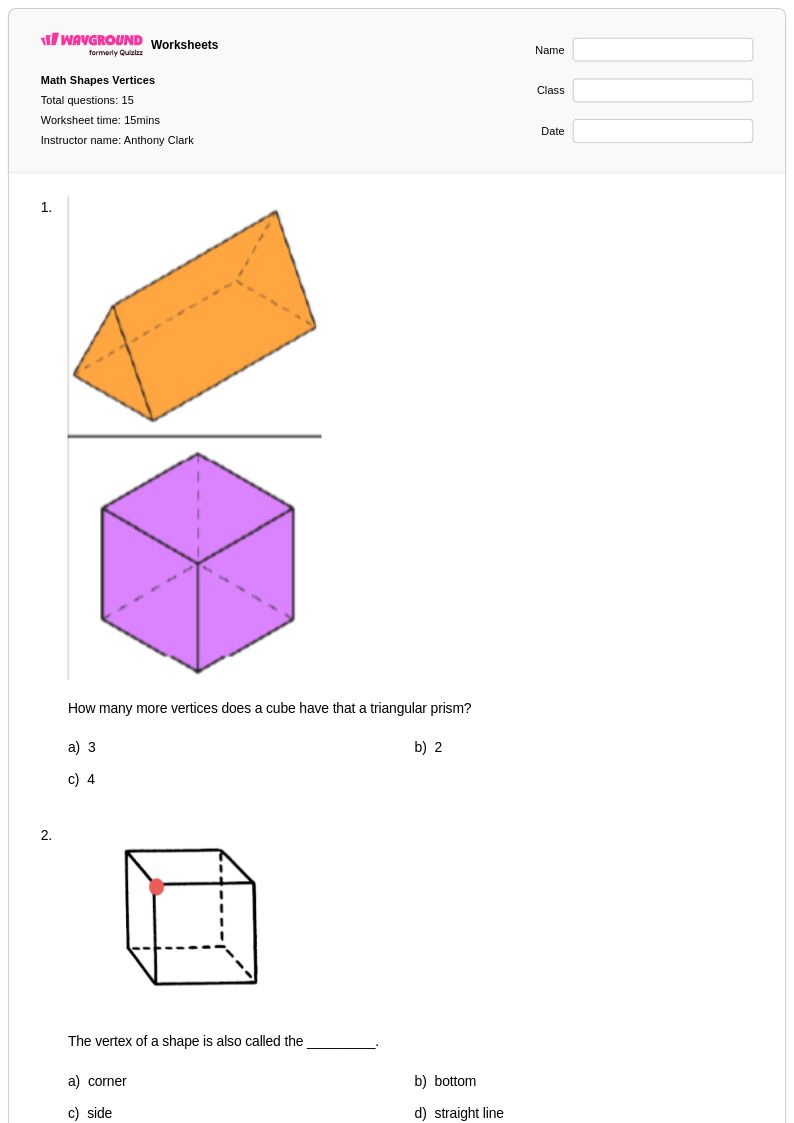
15Q
3rd - Uni
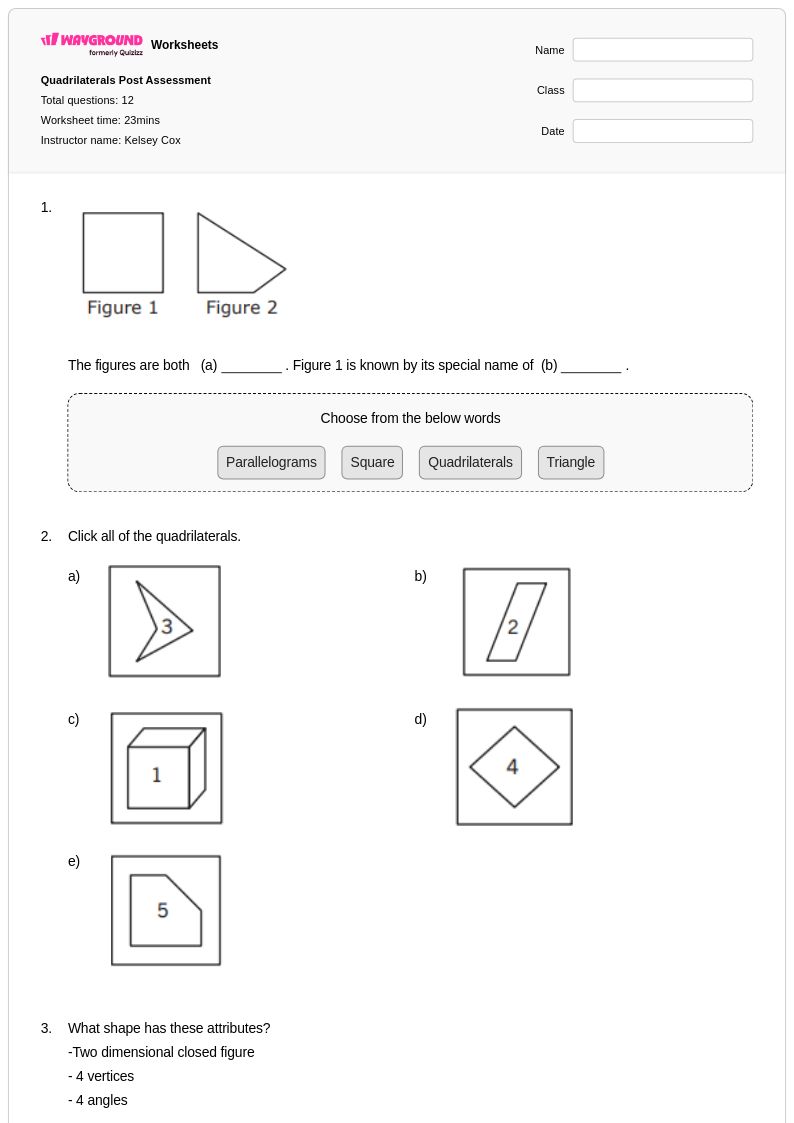
12Q
3rd
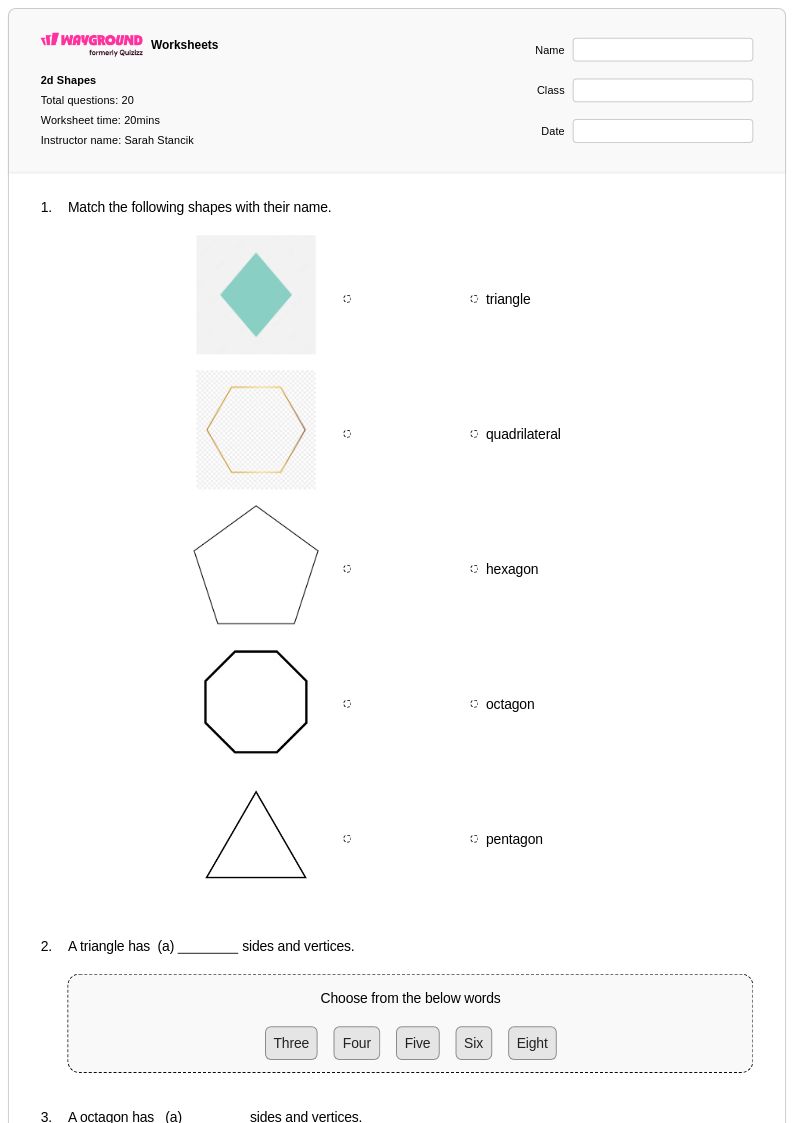
20Q
3rd

20Q
2nd - Uni
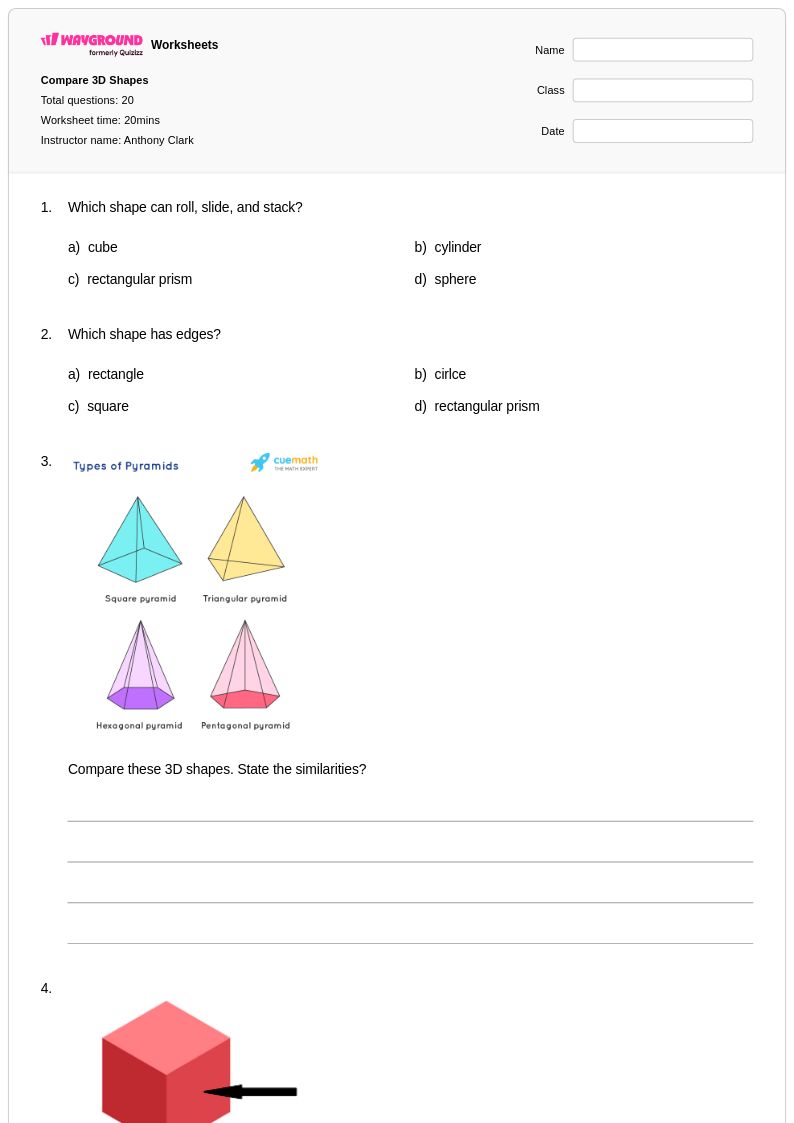
20Q
3rd - Uni
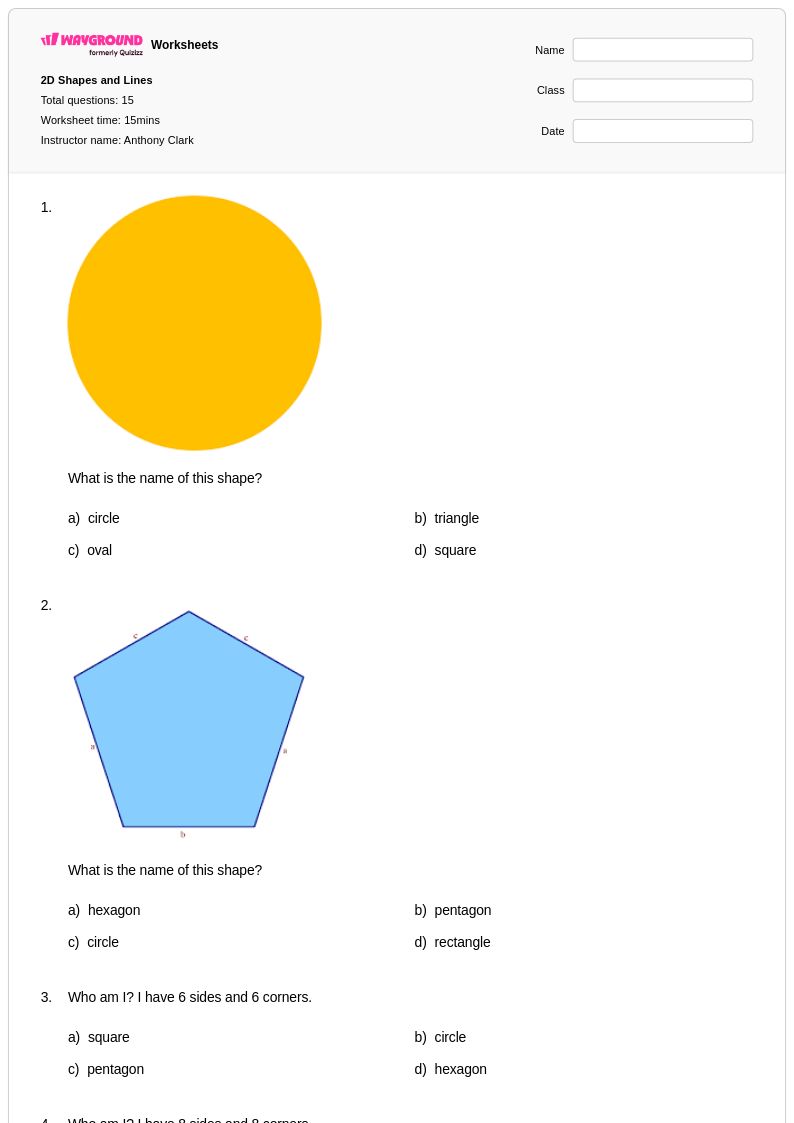
15Q
3rd - Uni

20Q
3rd - Uni
Explore outras planilhas de assuntos para ระดับ 3
สำรวจแผ่นงาน จุดยอด ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 3
แบบฝึกหัดเรื่องจุดยอดสำหรับนักเรียนชั้นประถมศึกษาปีที่ 3 จาก Wayground (เดิมชื่อ Quizizz) เป็นแบบฝึกหัดสำคัญที่ช่วยพัฒนาทักษะเรขาคณิตพื้นฐาน สนับสนุนการคิดเชิงพื้นที่และความเข้าใจทางคณิตศาสตร์ แบบฝึกหัดเหล่านี้เน้นการช่วยให้นักเรียนระบุ นับ และวิเคราะห์จุดยอดในรูปทรงสองมิติและสามมิติหลากหลายรูปแบบ สร้างคำศัพท์ทางเรขาคณิตที่สำคัญและพัฒนาความสามารถในการจดจำภาพ แบบฝึกหัดที่ออกแบบมาอย่างพิถีพิถันจะค่อยๆ ยากขึ้นทีละขั้น เริ่มจากรูปทรงง่ายๆ เช่น สามเหลี่ยมและสี่เหลี่ยม ไปจนถึงรูปหลายเหลี่ยมที่ซับซ้อนมากขึ้น ช่วยให้นักเรียนเข้าใจมากขึ้นว่าจุดยอดกำหนดรูปทรงเรขาคณิตอย่างไร แบบฝึกหัดแต่ละแผ่นมีเฉลยคำตอบเพื่อสนับสนุนการเรียนรู้ด้วยตนเองและการประเมินตนเอง และในรูปแบบไฟล์ PDF ฟรี เข้าถึงได้ง่ายสำหรับการใช้งานในห้องเรียนและการฝึกฝนที่บ้าน
Wayground (เดิมชื่อ Quizizz) ช่วยให้ครูมีแหล่งข้อมูลนับล้านที่สร้างโดยนักการศึกษาโดยเฉพาะสำหรับการสอนเรื่องจุดยอดในชั้นประถมศึกษาปีที่ 3 มีฟังก์ชันการค้นหาและการกรองที่มีประสิทธิภาพ ช่วยค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานหลักสูตรและวัตถุประสงค์การเรียนรู้ที่เฉพาะเจาะจง เครื่องมือปรับระดับความยากง่ายของแพลตฟอร์มนี้ช่วยให้ครูสามารถปรับแต่งกิจกรรมที่เน้นจุดยอดให้เหมาะสมกับความต้องการการเรียนรู้ที่หลากหลาย ไม่ว่าจะเป็นการแก้ไขปัญหาสำหรับนักเรียนที่เรียนรู้ช้า หรือการเสริมสร้างทักษะสำหรับผู้เรียนที่มีความสามารถสูง ครูสามารถเข้าถึงทั้งรูปแบบสิ่งพิมพ์และดิจิทัลได้อย่างราบรื่น รวมถึงไฟล์ PDF ที่ดาวน์โหลดได้ ทำให้การวางแผนบทเรียนมีประสิทธิภาพและยืดหยุ่นในสภาพแวดล้อมการสอนที่หลากหลาย ชุดแบบฝึกหัดที่ครอบคลุมเหล่านี้สนับสนุนการฝึกฝนทักษะและการประเมินอย่างเป็นระบบ ช่วยให้ครูติดตามความก้าวหน้าของนักเรียนในการเรียนรู้แนวคิดทางเรขาคณิต พร้อมทั้งให้การช่วยเหลือที่ตรงเป้าหมายเพื่อให้แน่ใจว่าผู้เรียนทุกคนพัฒนาความเข้าใจพื้นฐานที่แข็งแกร่งเกี่ยวกับจุดยอดและบทบาทของจุดยอดในการระบุรูปทรง
