
52 Q
7th
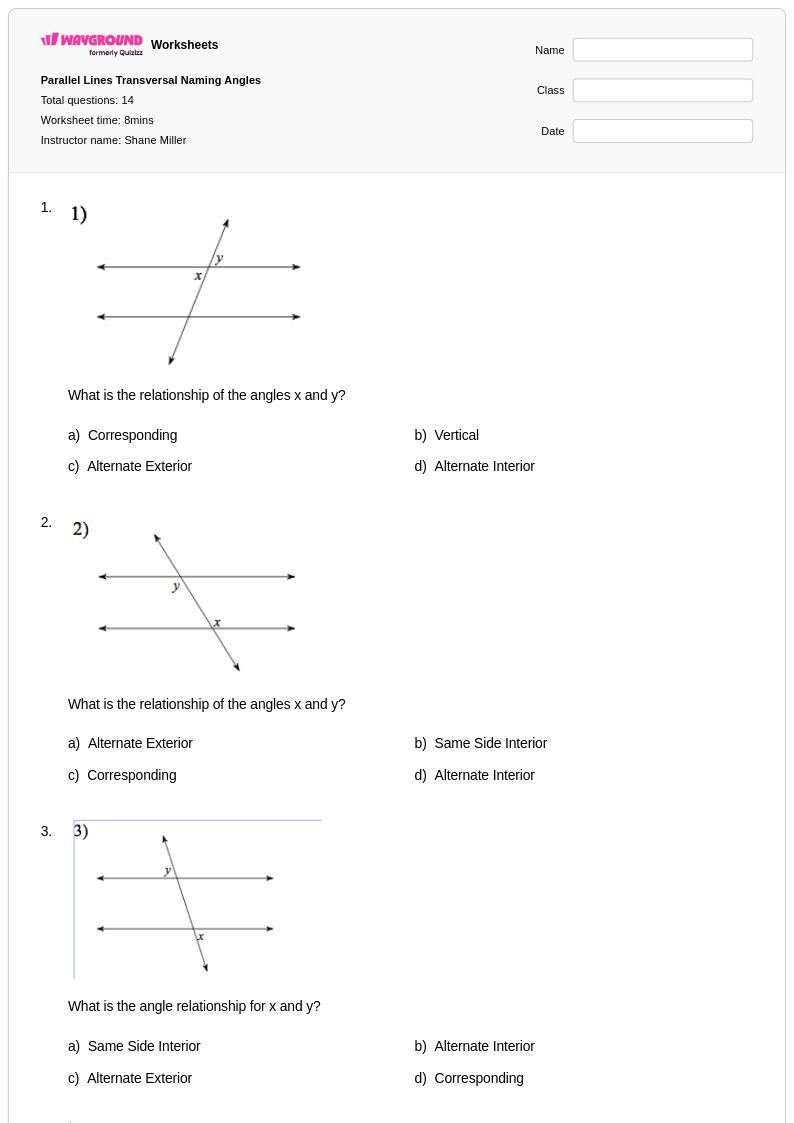
14 Q
7th - 10th
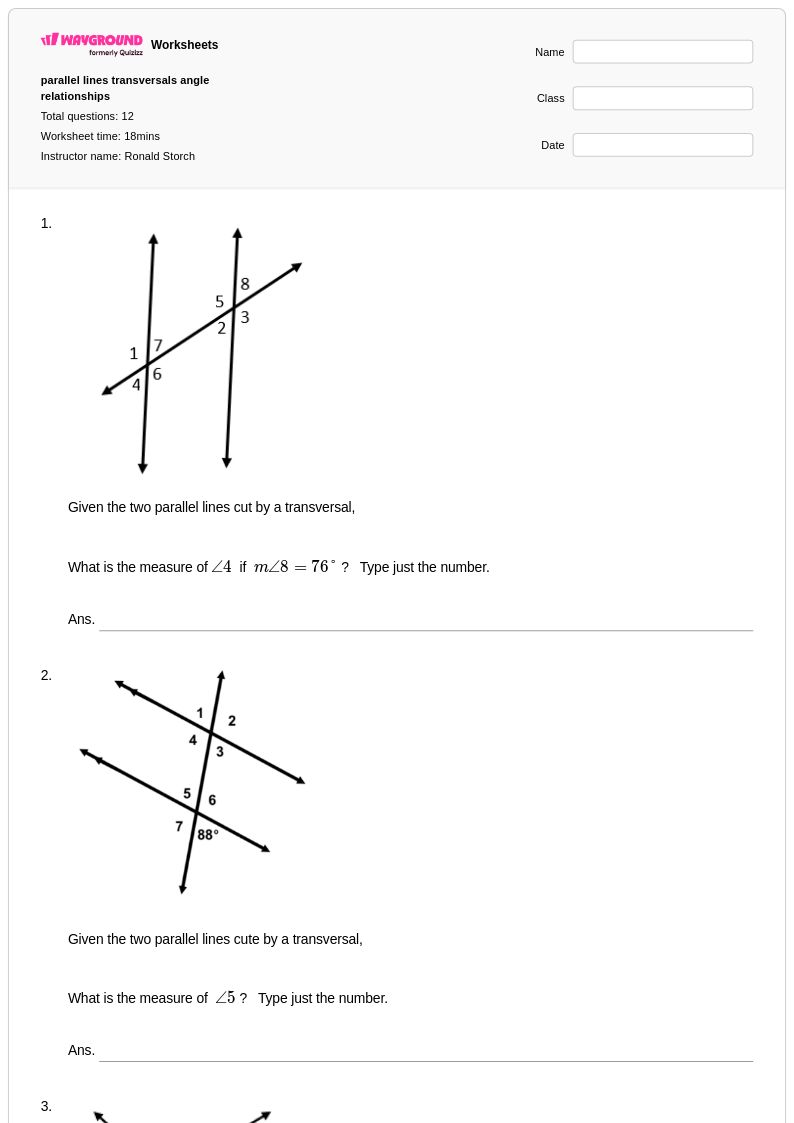
12 Q
7th
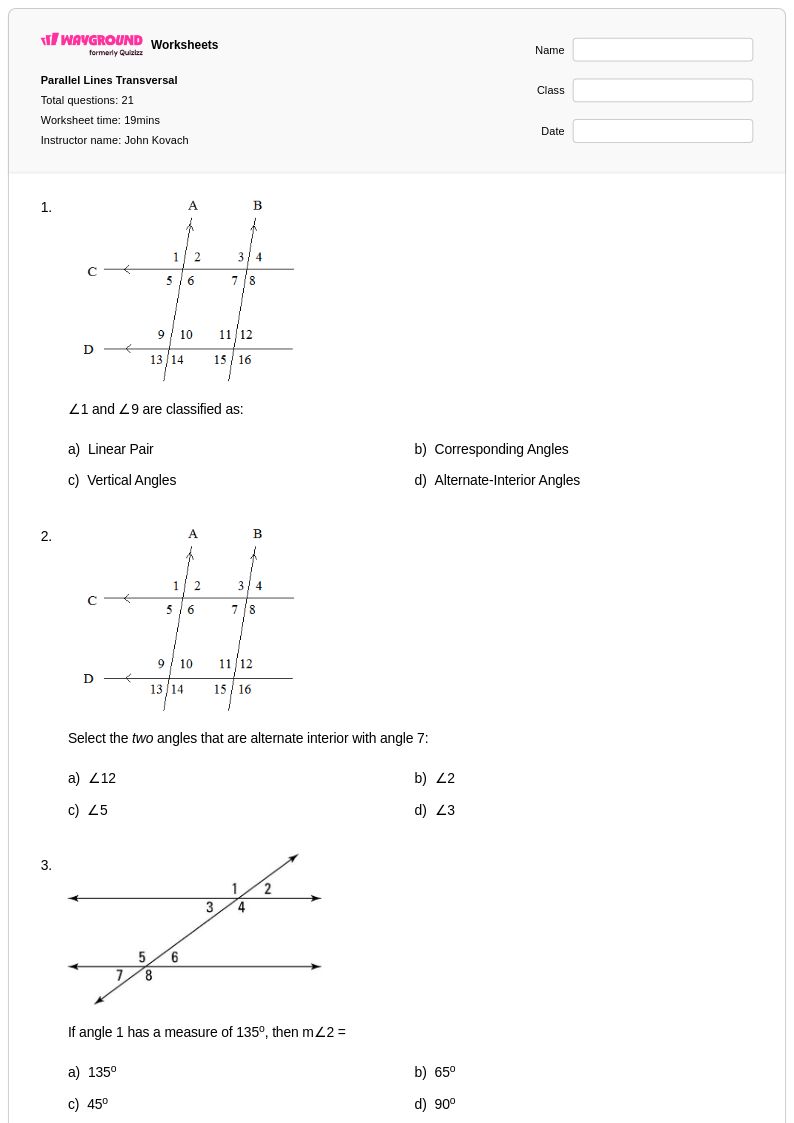
21 Q
6th - Uni

20 Q
5th - 8th
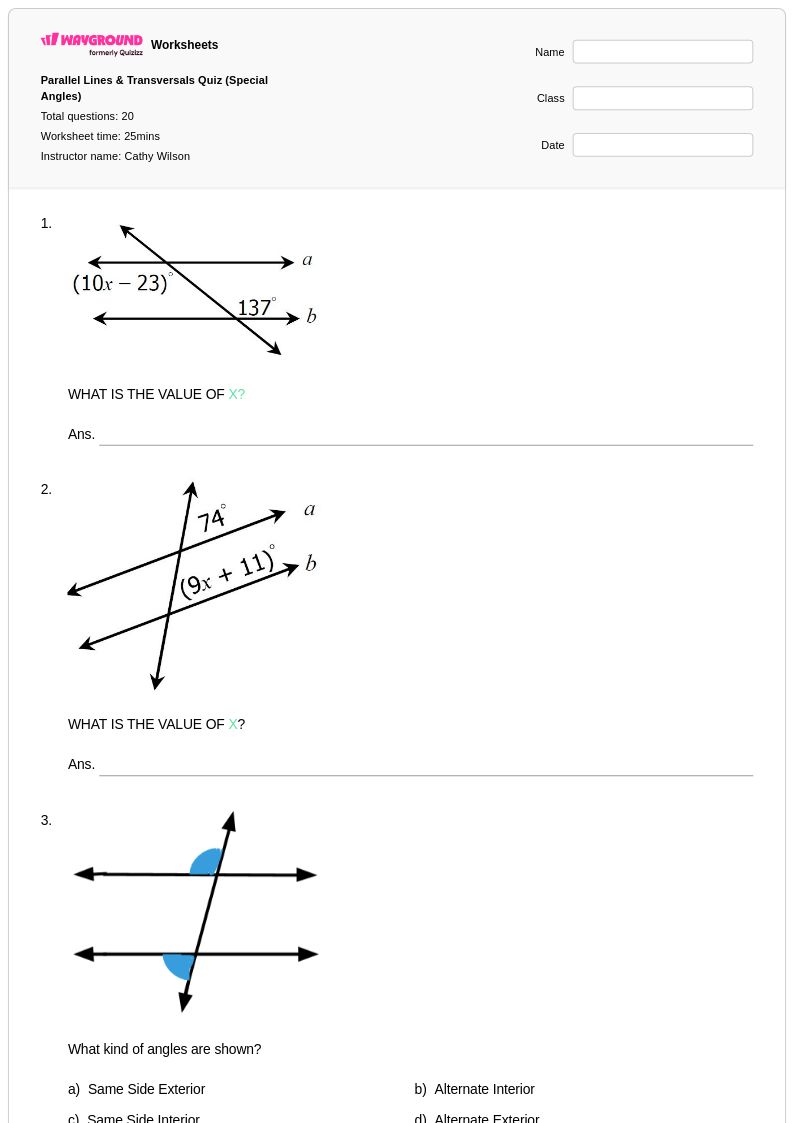
20 Q
7th
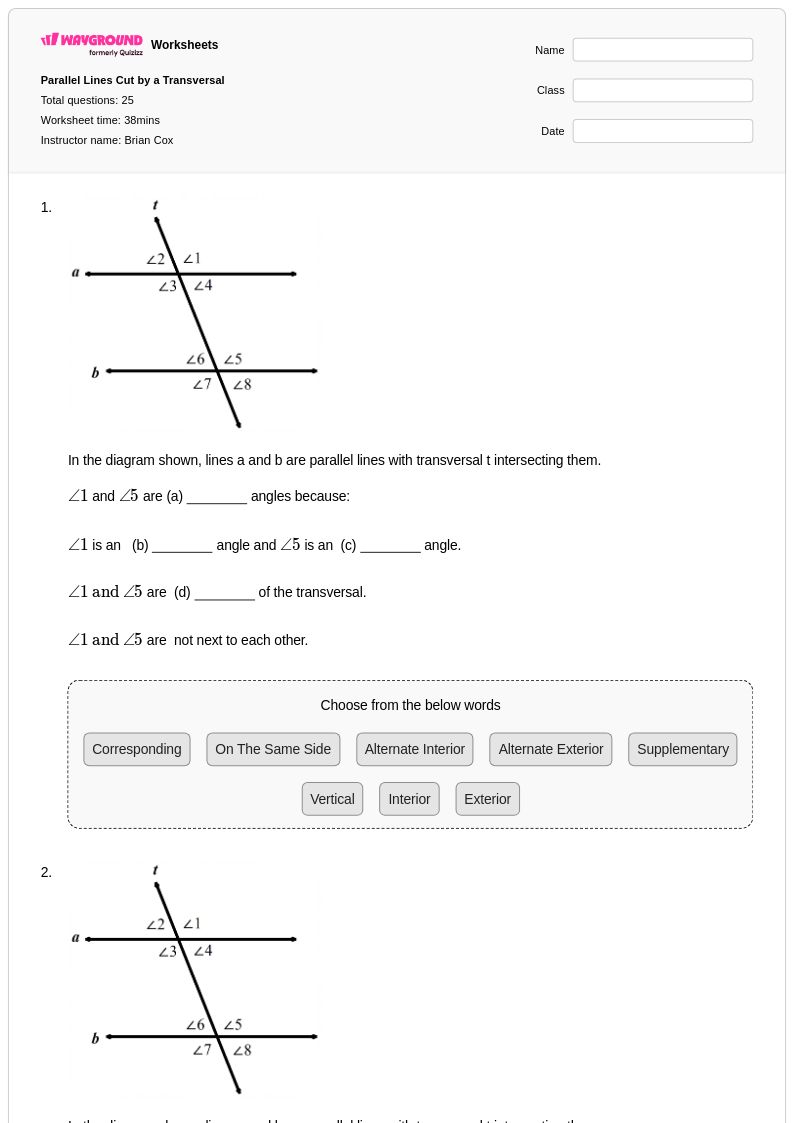
25 Q
6th - 8th
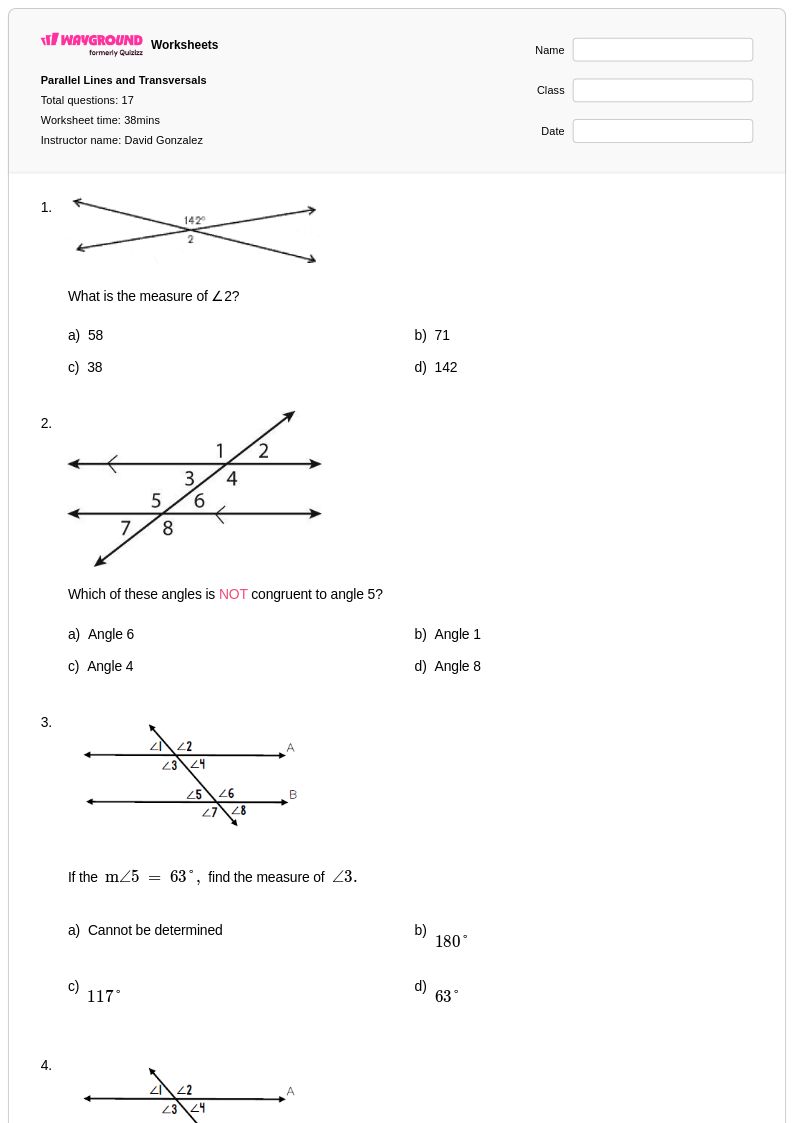
17 Q
7th
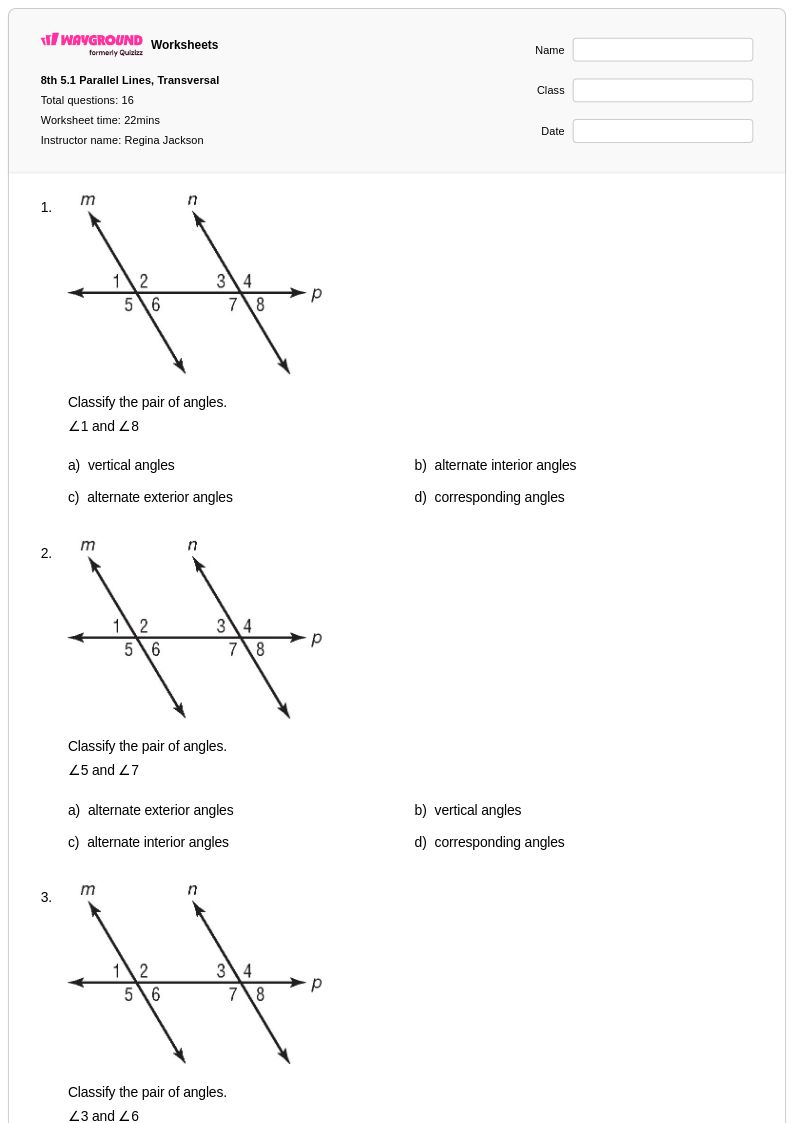
16 Q
7th
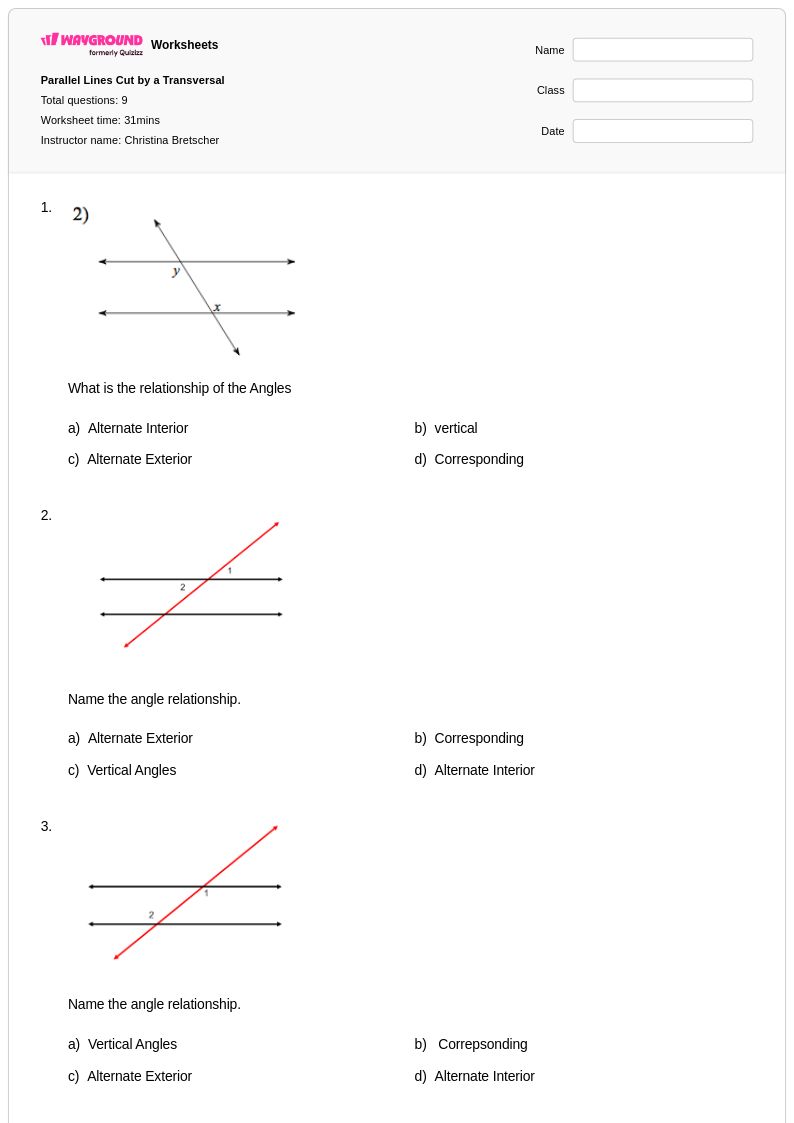
9 Q
7th
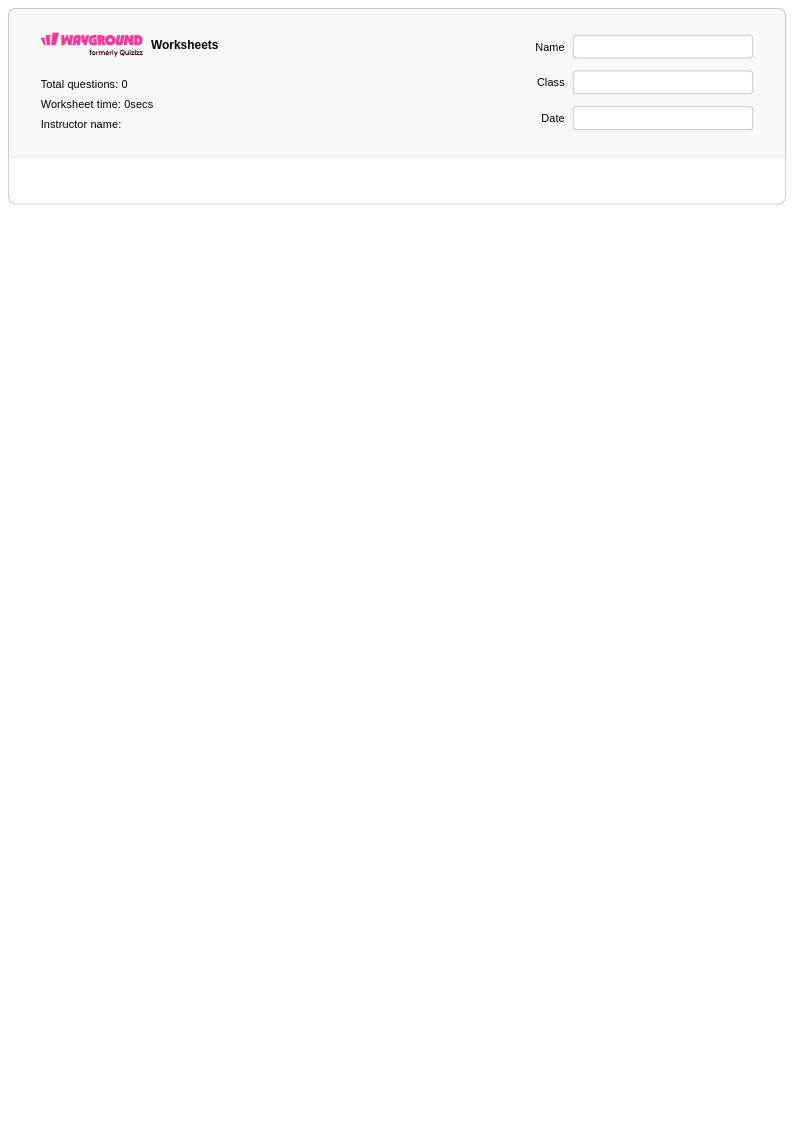
24 Q
7th
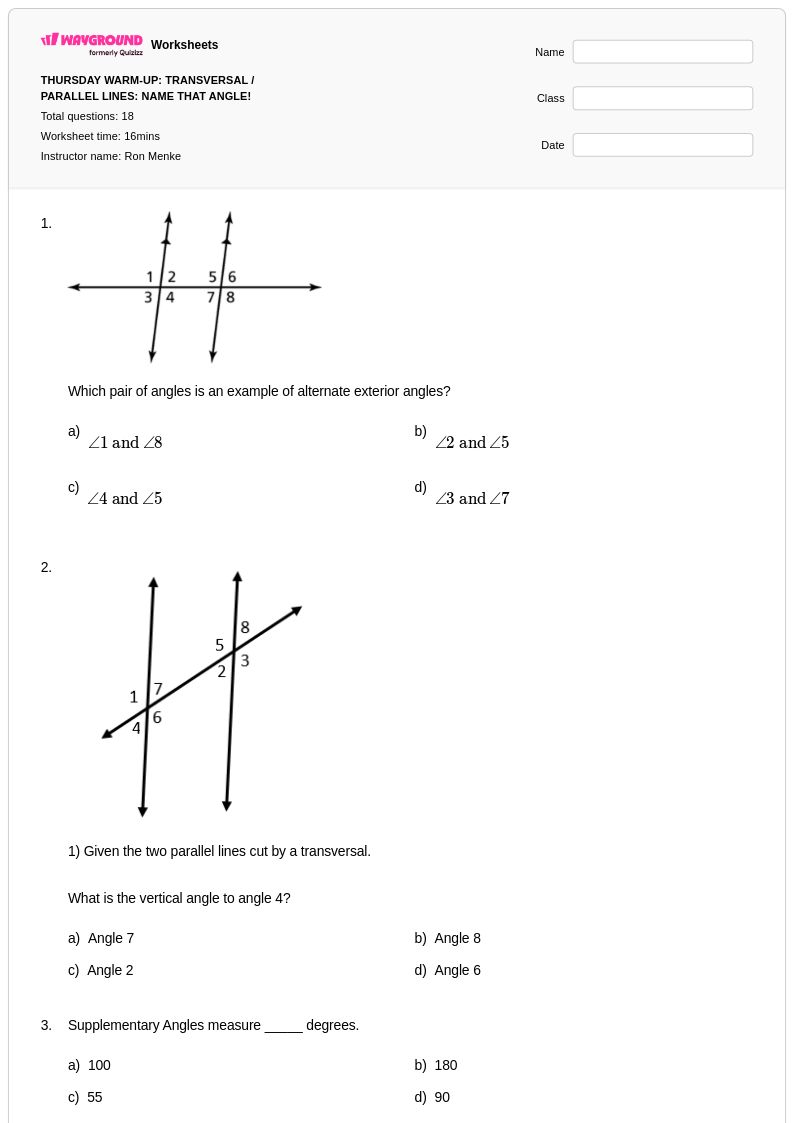
18 Q
6th - 8th

10 Q
7th - 9th
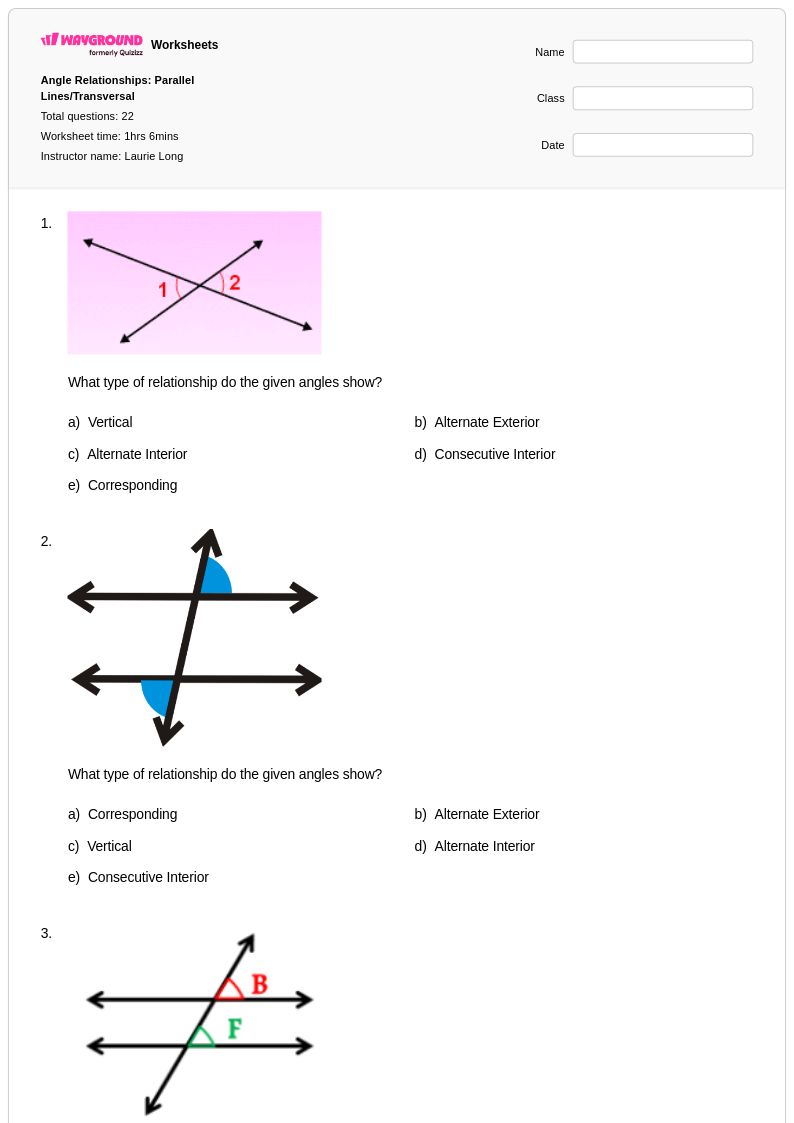
22 Q
7th - 8th
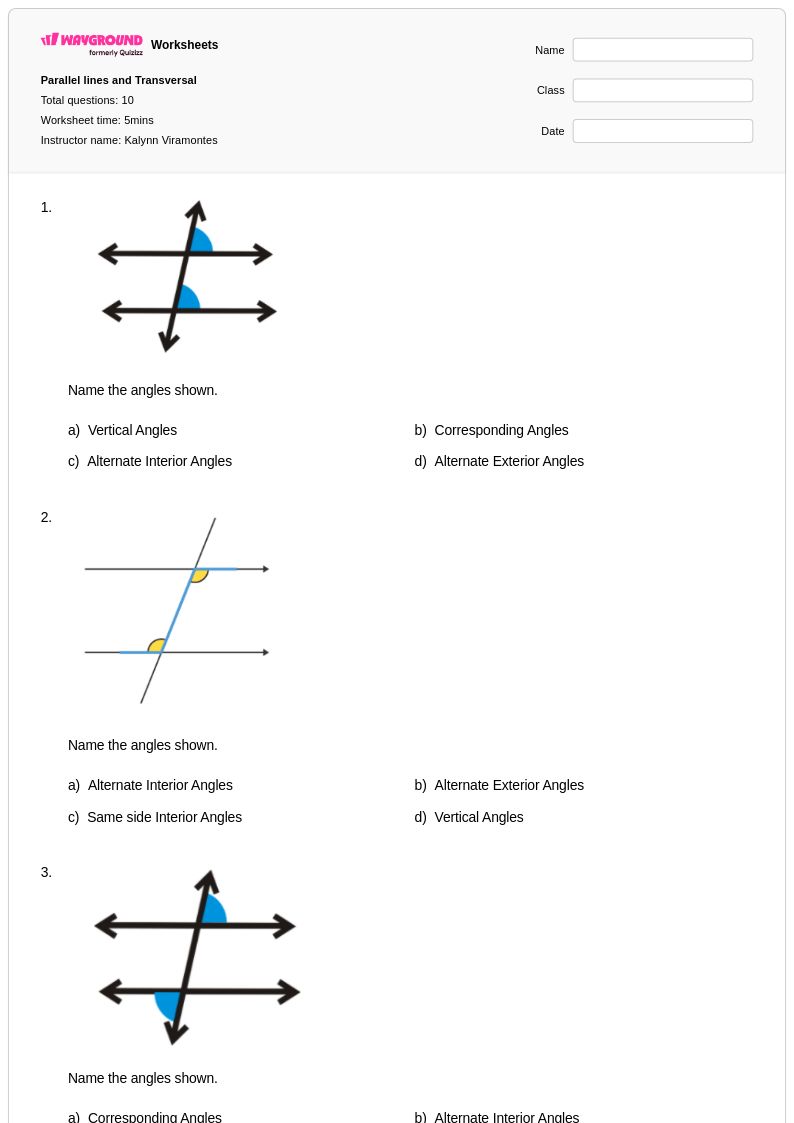
10 Q
6th - 8th
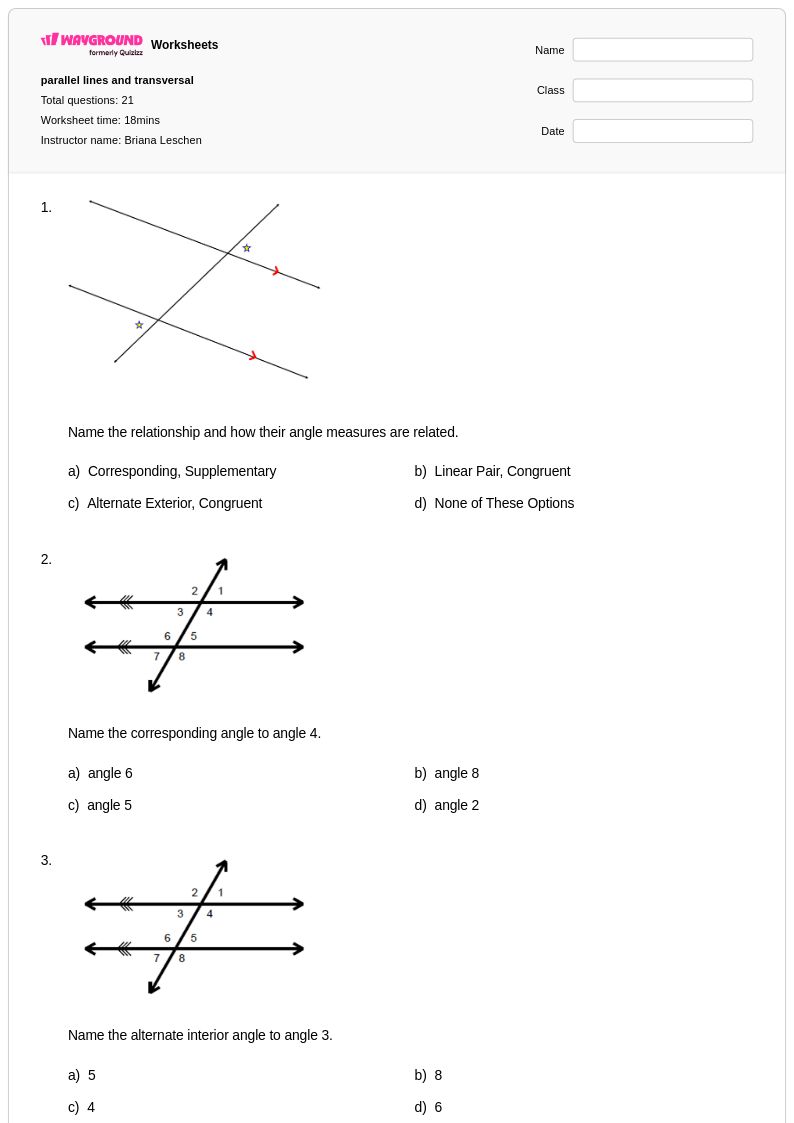
21 Q
6th - 8th
10 Q
7th
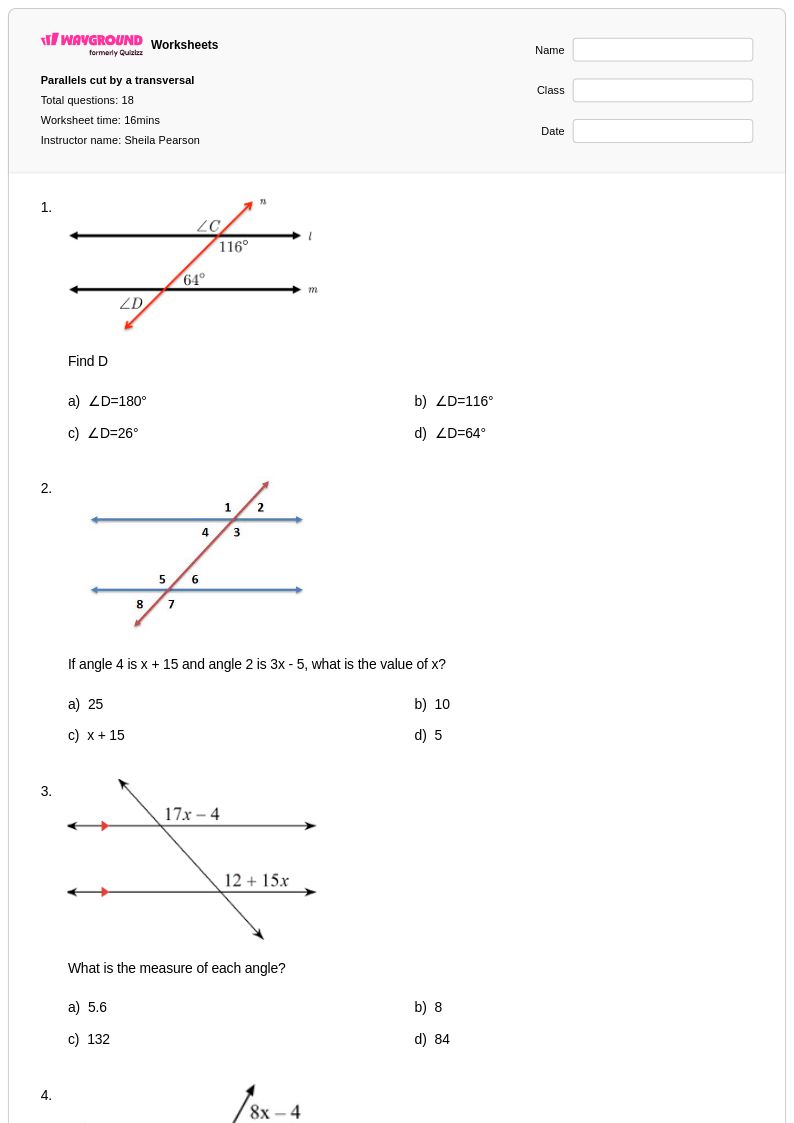
18 Q
7th

12 Q
7th - 8th
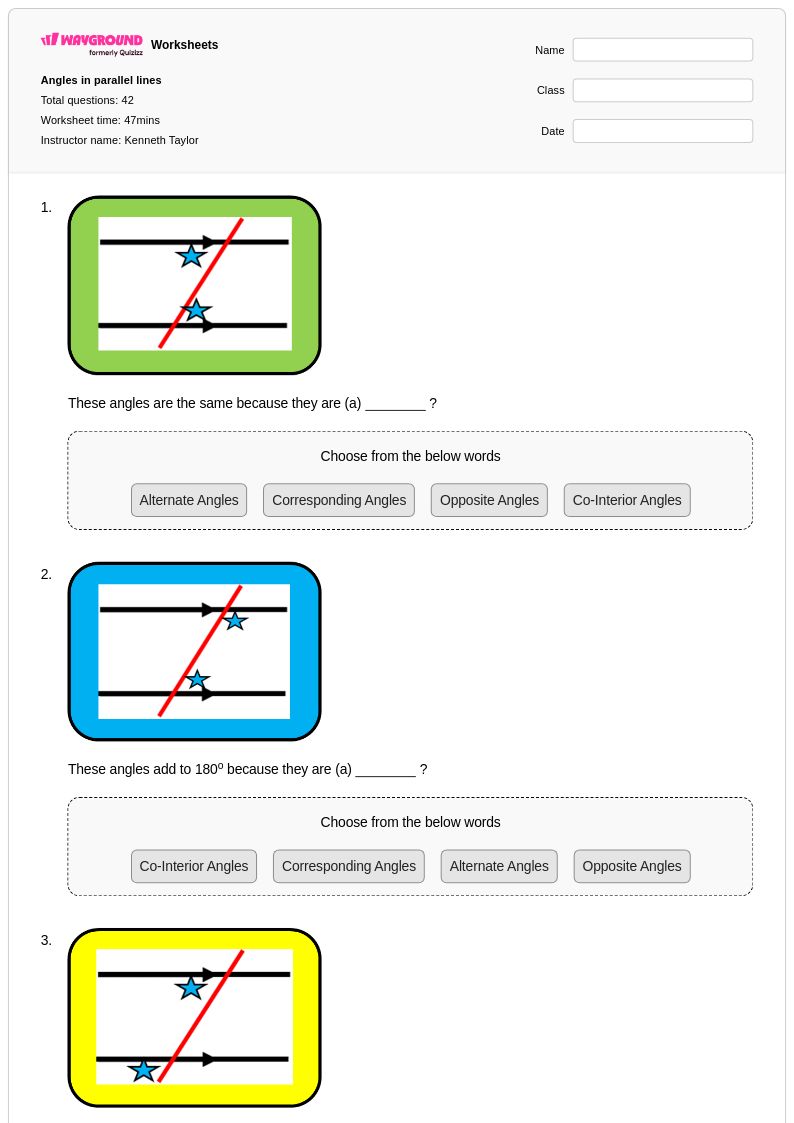
42 Q
6th - 9th
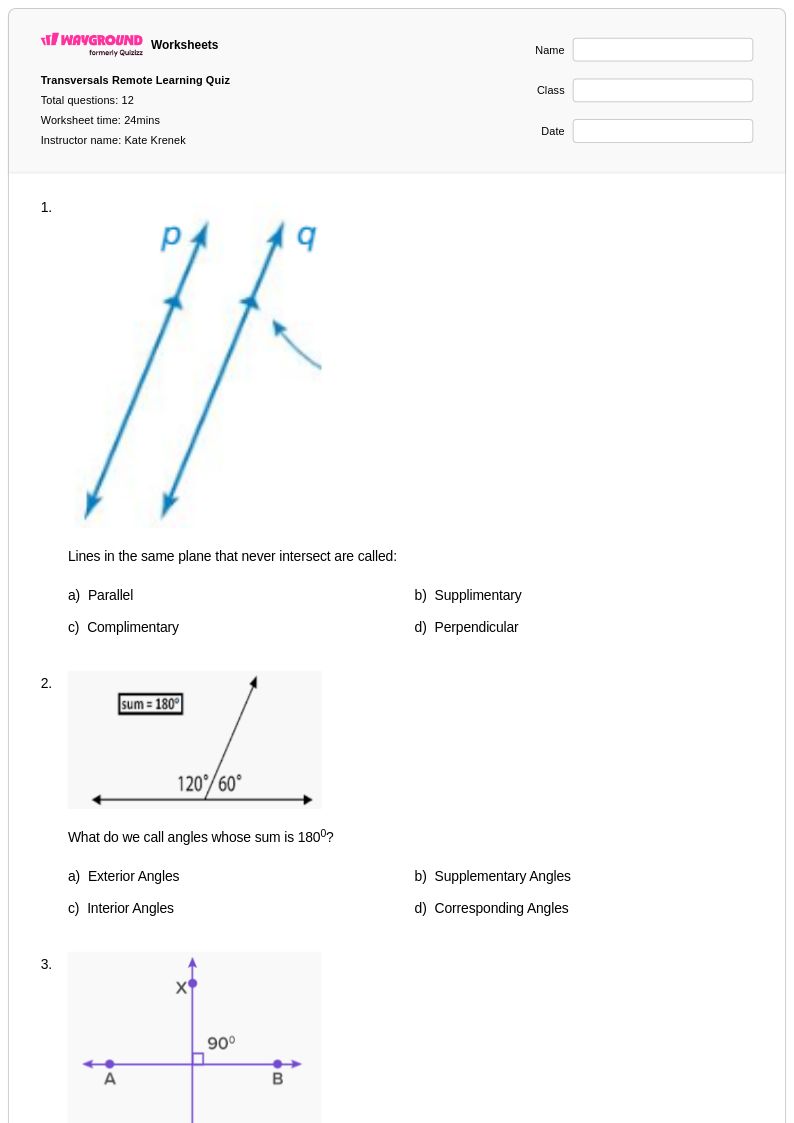
12 Q
7th - 8th
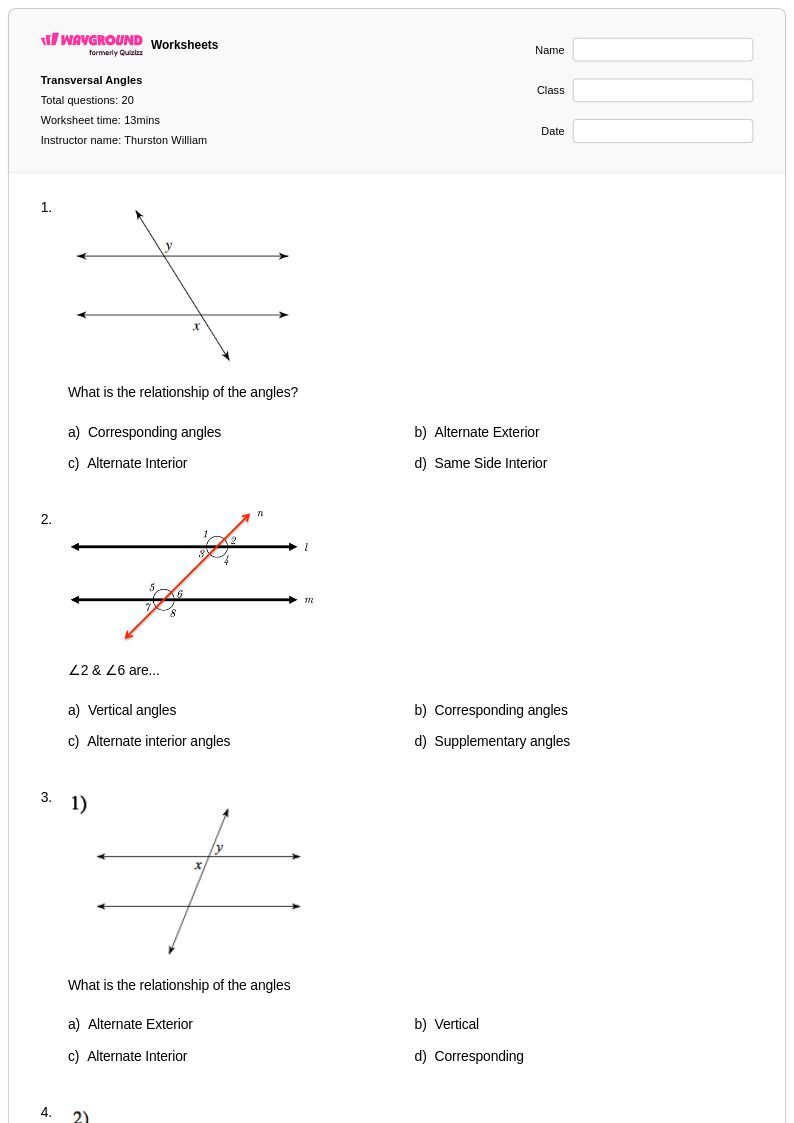
20 Q
6th - 8th
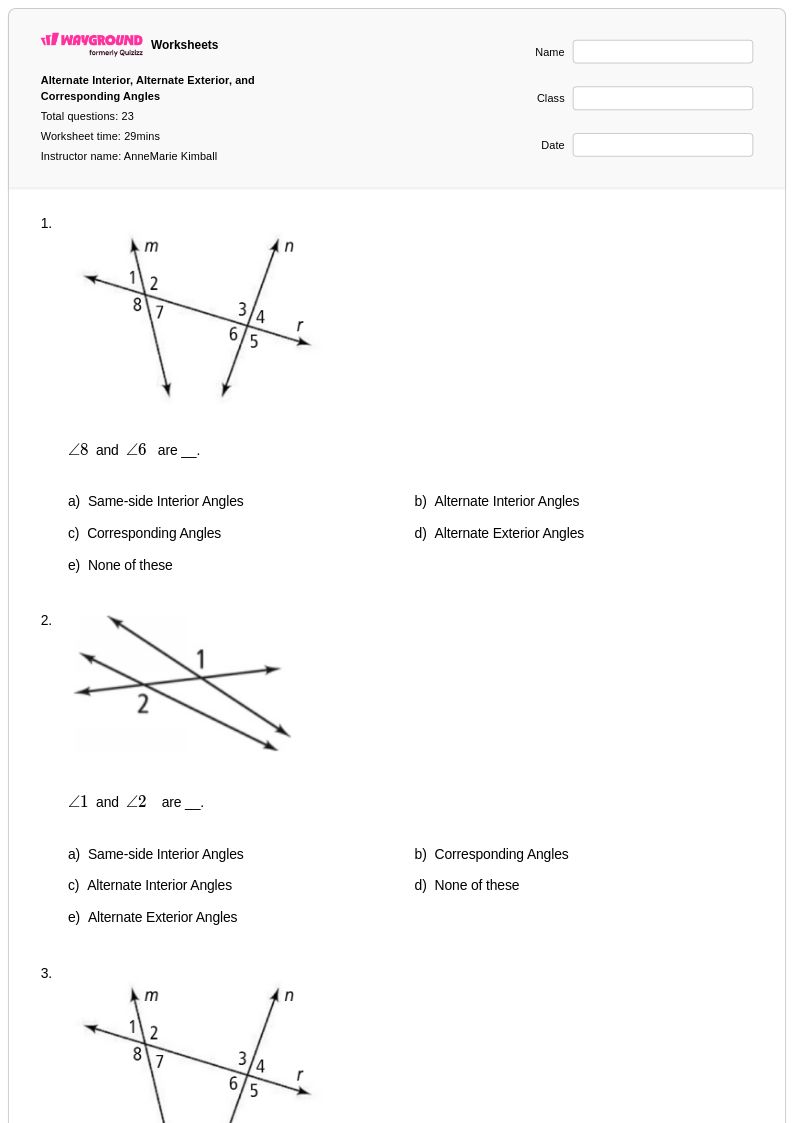
23 Q
7th
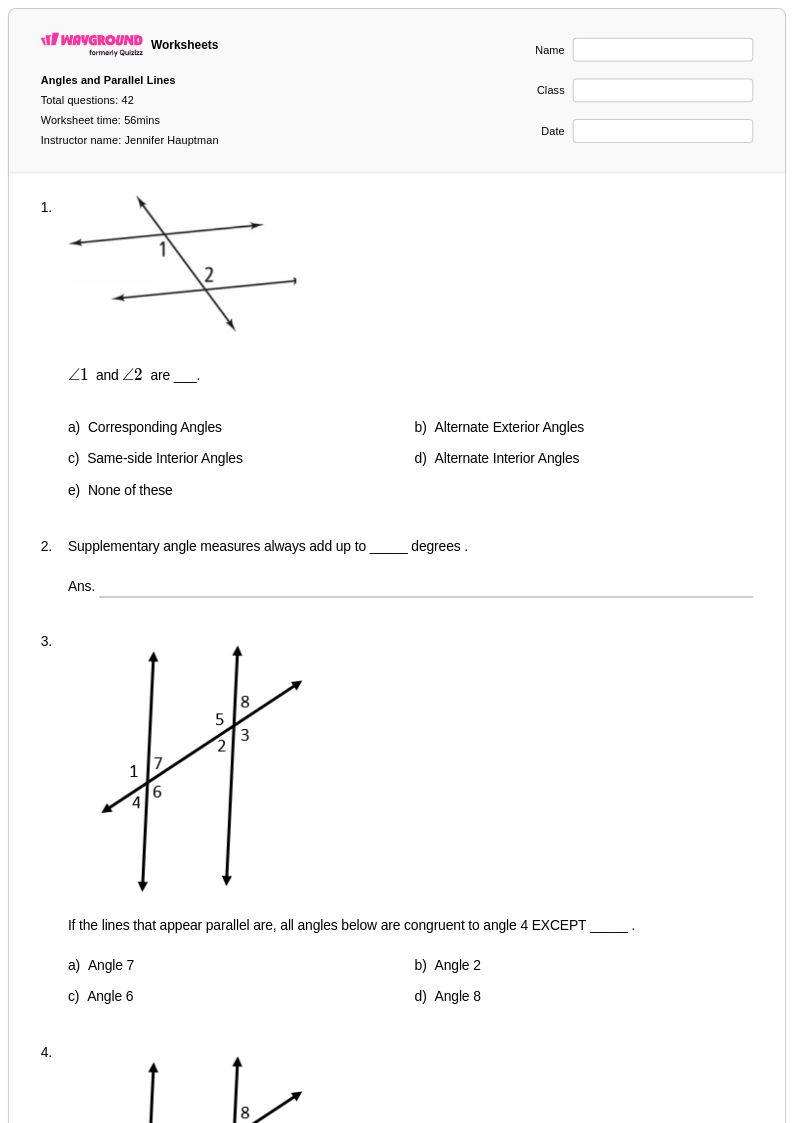
42 Q
8th
Explore Other Subject Worksheets for ระดับ 7
สำรวจแผ่นงาน เส้นตัดขวางของเส้นขนาน ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 7
แบบฝึกหัดเรื่องเส้นตัดขวางของเส้นขนานสำหรับนักเรียนชั้น ม.1 จาก Wayground เป็นแบบฝึกหัดที่ครอบคลุมเกี่ยวกับแนวคิดพื้นฐานที่สุดอย่างหนึ่งของเรขาคณิต แบบฝึกหัดเหล่านี้ได้รับการออกแบบอย่างพิถีพิถัน ช่วยให้นักเรียนเชี่ยวชาญในการระบุและการประยุกต์ใช้ความสัมพันธ์ของมุมที่เกิดขึ้นเมื่อเส้นตัดขวางตัดกับเส้นขนานสองเส้น รวมถึงมุมที่สมนัยกัน มุมภายในสลับ มุมภายนอกสลับ และมุมภายในร่วม นักเรียนจะเสริมสร้างทักษะการวิเคราะห์โดยการทำแบบฝึกหัดที่ต้องคำนวณขนาดมุมที่หายไป ระบุคู่มุมที่เท่ากันและมุมเสริม และประยุกต์ใช้ความสัมพันธ์เหล่านี้เพื่อแก้ปัญหาทางเรขาคณิตในชีวิตจริง แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียด และมีให้ดาวน์โหลดฟรีในรูปแบบ PDF ที่สะดวก ทำให้ครูผู้สอนสามารถแจกจ่ายสื่อการเรียนการสอนที่ช่วยสร้างความสามารถในการให้เหตุผลทางเรขาคณิตที่สำคัญได้อย่างง่ายดาย
คลังแบบฝึกหัดเรื่องเส้นตัดขวางที่สร้างโดยครูผู้สอนจำนวนมากของ Wayground มีทรัพยากรนับล้านรายการพร้อมความสามารถในการค้นหาและกรองข้อมูลที่มีประสิทธิภาพ ซึ่งสอดคล้องกับมาตรฐานคณิตศาสตร์ระดับรัฐและระดับชาติสำหรับเรขาคณิตชั้น ม.1 ครูสามารถปรับการสอนให้เหมาะสมกับระดับความสามารถของนักเรียนได้ง่ายๆ โดยเลือกใช้แบบฝึกหัดที่หลากหลาย ตั้งแต่แบบฝึกหัดพื้นฐานเกี่ยวกับการระบุค่ามุม ไปจนถึงโจทย์ปัญหาที่ซับซ้อนหลายขั้นตอนซึ่งเกี่ยวข้องกับนิพจน์พีชคณิตและการพิสูจน์ทางเรขาคณิต เครื่องมือปรับแต่งที่ยืดหยุ่นของแพลตฟอร์มช่วยให้ครูสามารถแก้ไขแบบฝึกหัดที่มีอยู่ หรือผสมผสานองค์ประกอบจากแหล่งข้อมูลหลายแหล่ง เพื่อตอบสนองความต้องการเฉพาะของห้องเรียน ไม่ว่าจะเป็นการแนะนำทักษะเบื้องต้น การแก้ไขปัญหาเฉพาะจุด หรือกิจกรรมเสริมความรู้ขั้นสูง แบบฝึกหัดที่ครอบคลุมเหล่านี้มีให้เลือกทั้งแบบพิมพ์และแบบดิจิทัล ช่วยให้การวางแผนบทเรียนง่ายขึ้น ในขณะเดียวกันก็มอบโอกาสที่หลากหลายให้นักเรียนได้ฝึกฝนและเชี่ยวชาญความสัมพันธ์ทางเรขาคณิตที่สำคัญ ซึ่งเป็นรากฐานของแนวคิดทางคณิตศาสตร์ขั้นสูง
