
10 คิว
8th
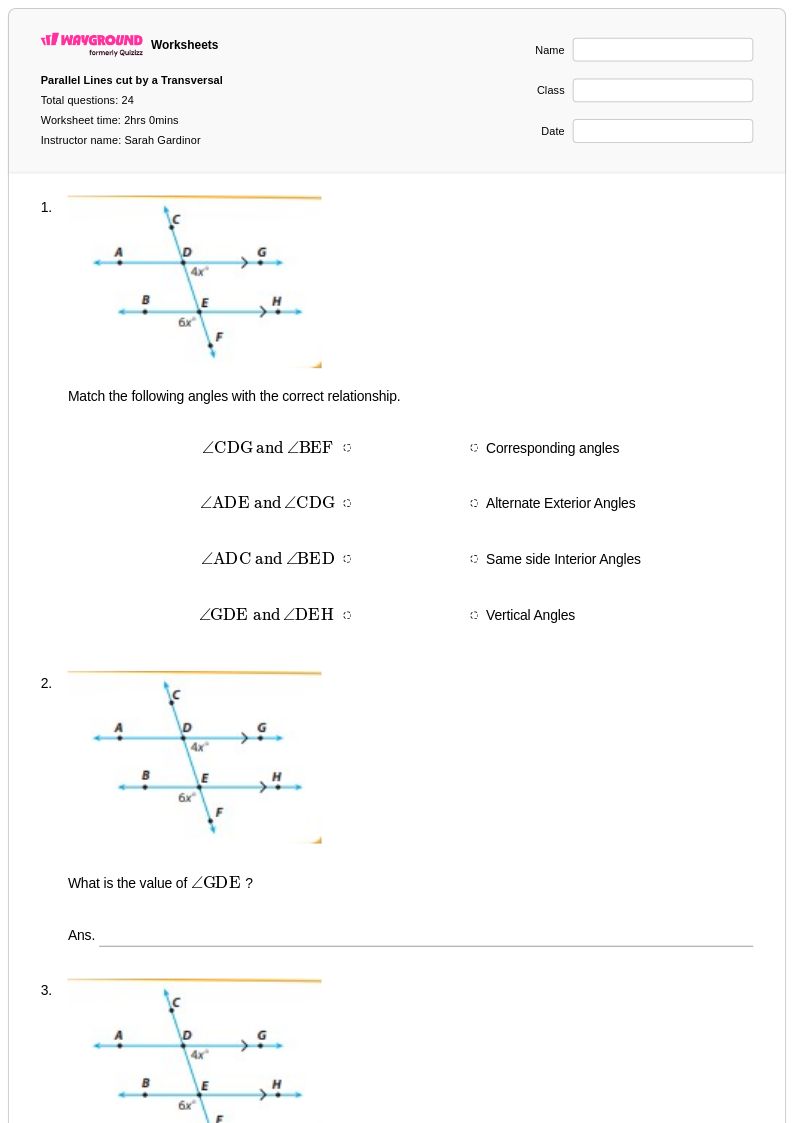
24 คิว
8th

9 คิว
8th
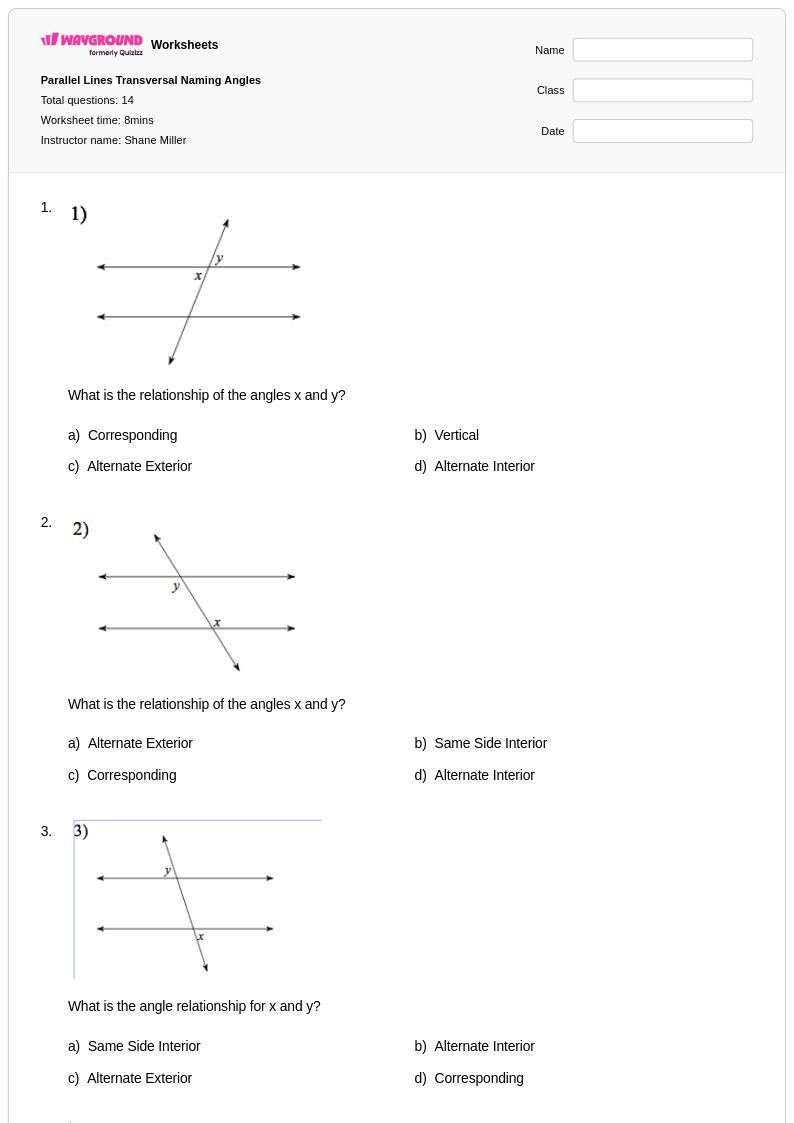
14 คิว
7th - 10th

25 คิว
8th

57 คิว
8th
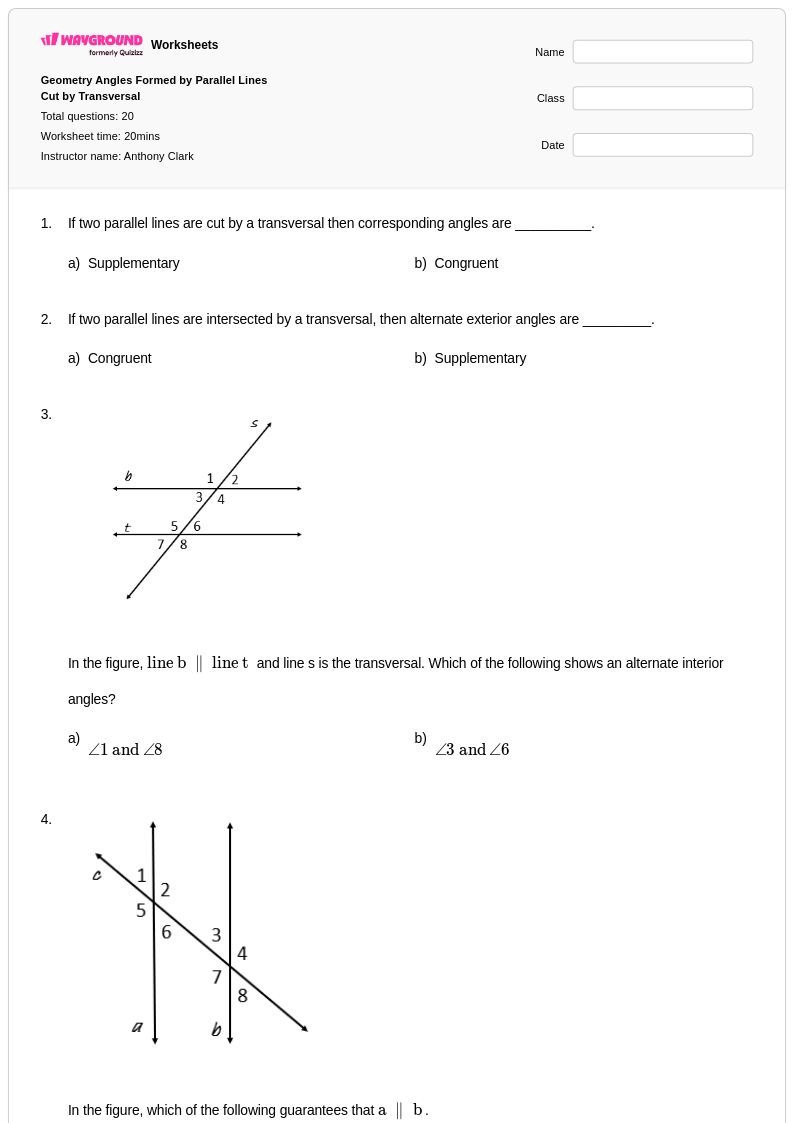
20 คิว
8th - Uni
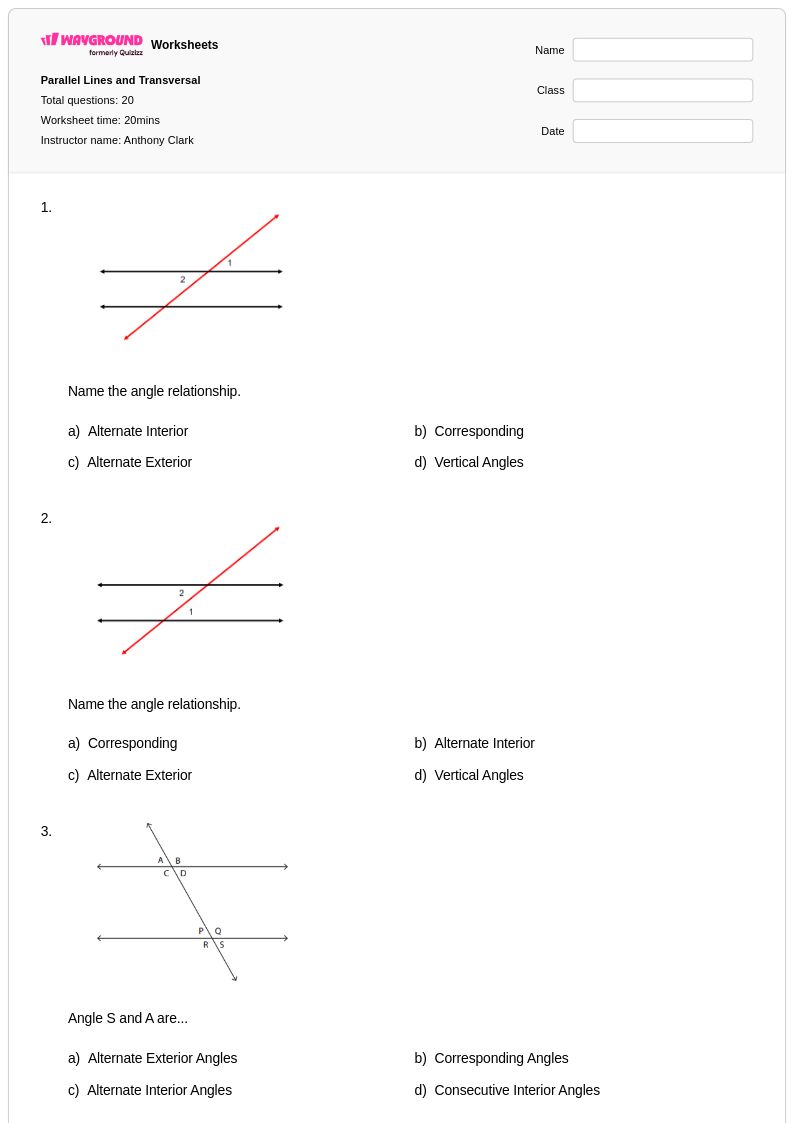
20 คิว
8th - Uni

21 คิว
8th - 12th
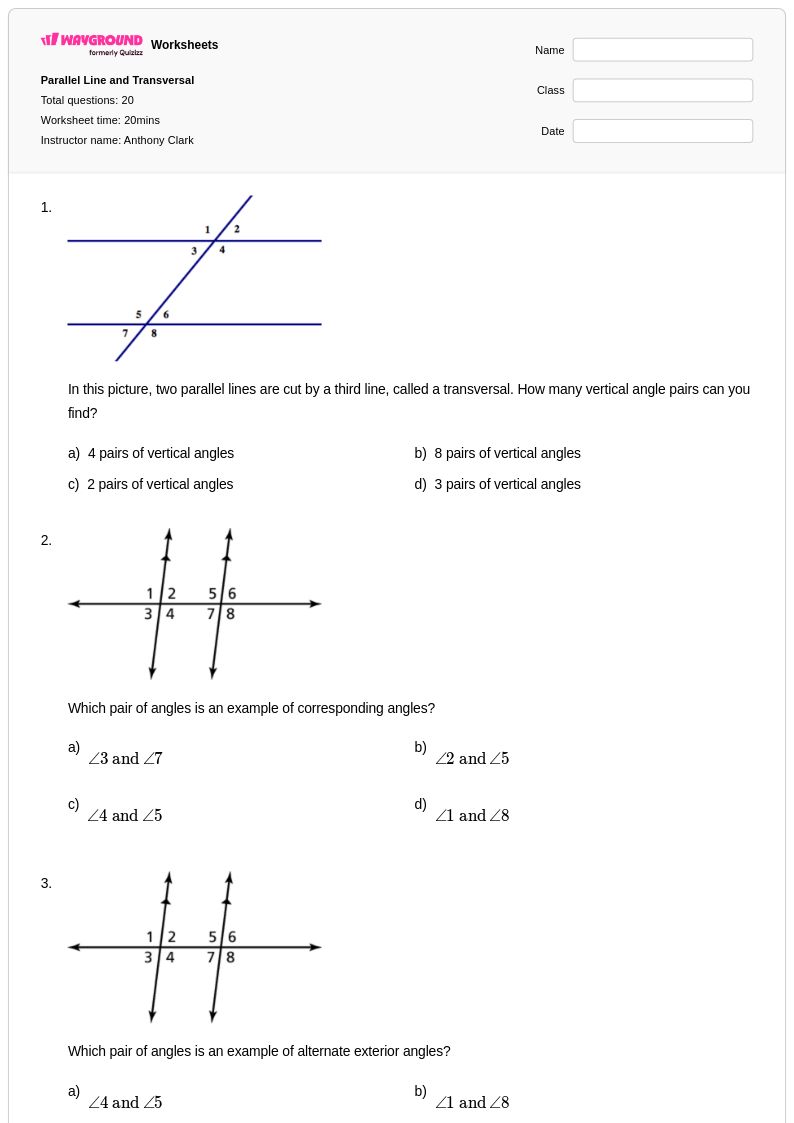
20 คิว
8th - Uni
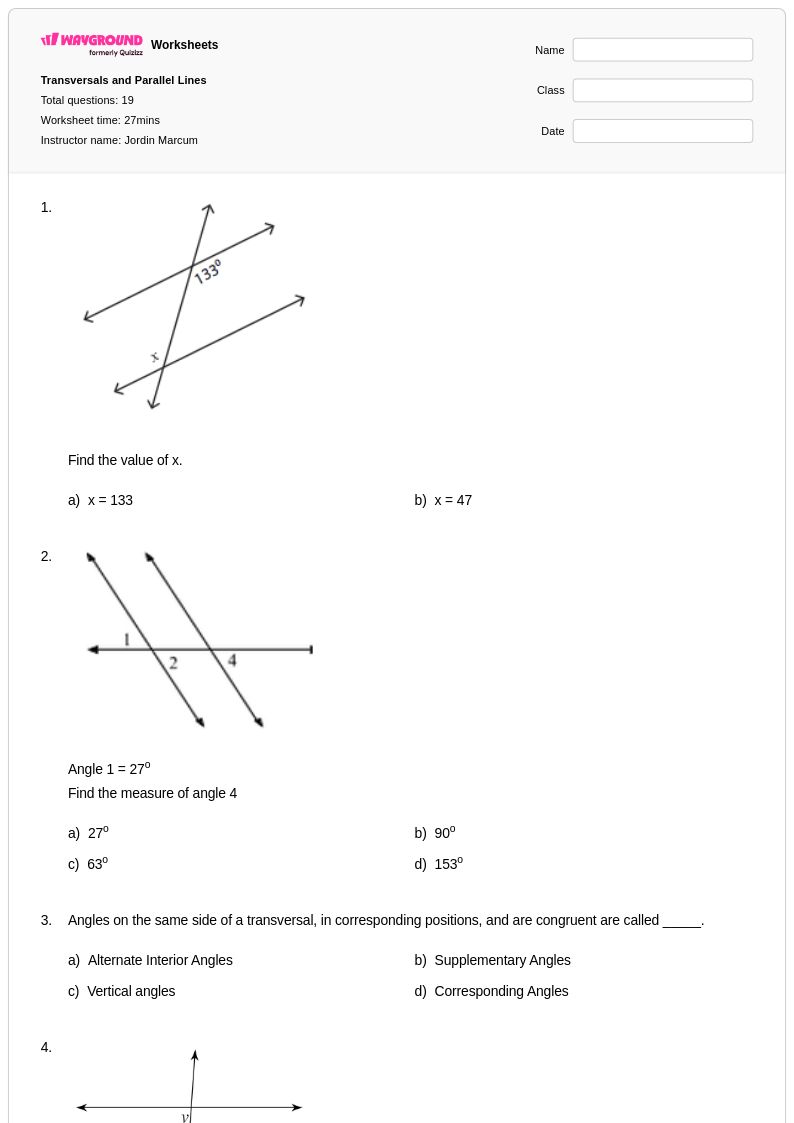
19 คิว
8th
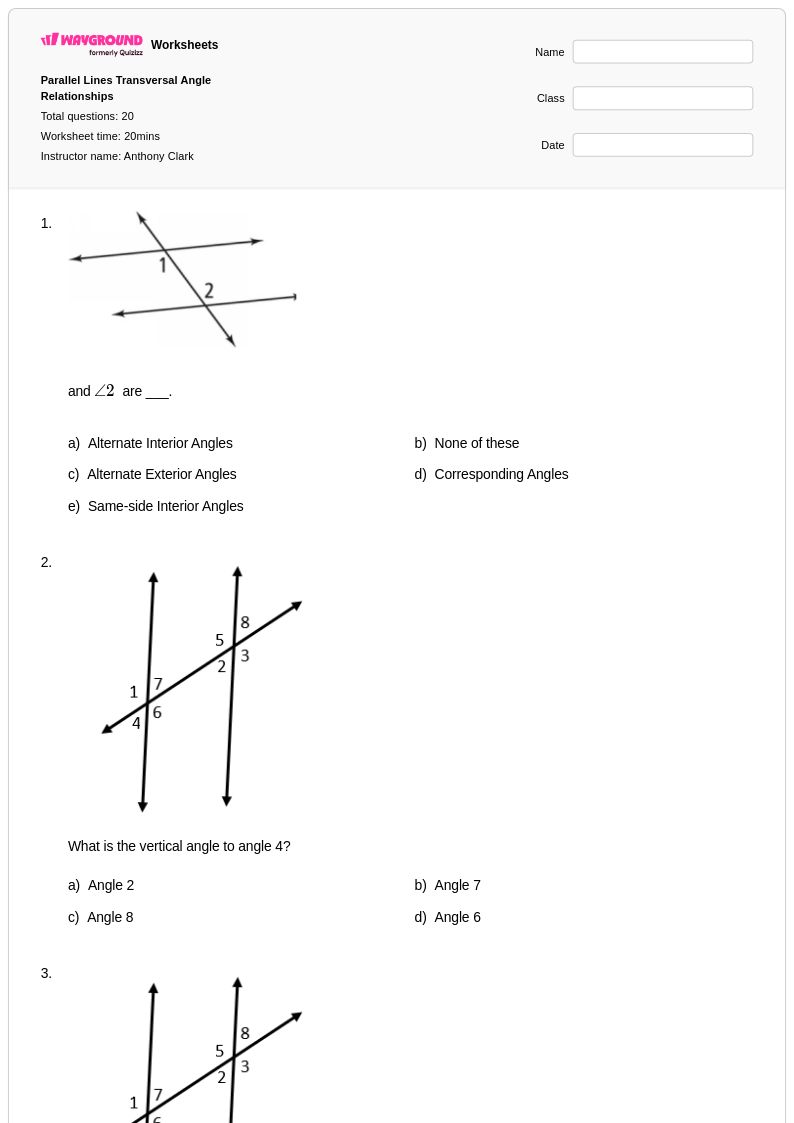
20 คิว
8th - Uni

20 คิว
8th - Uni

20 คิว
8th - Uni
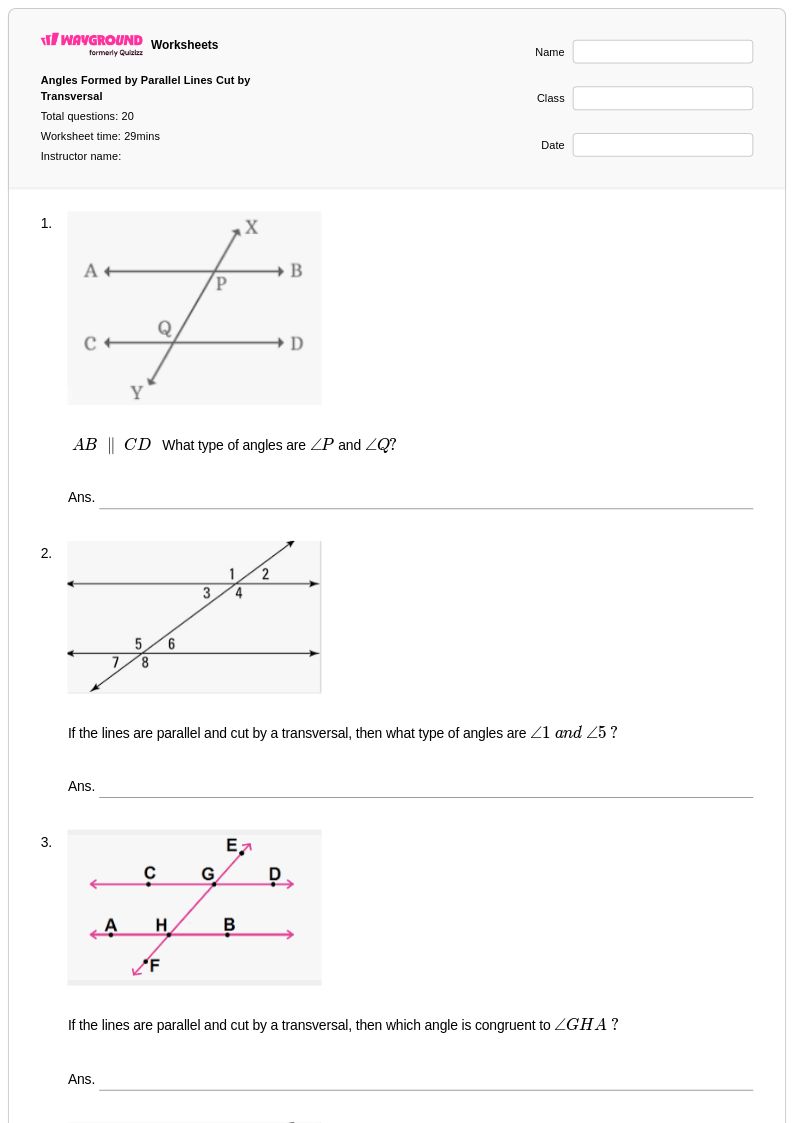
20 คิว
8th - 11th
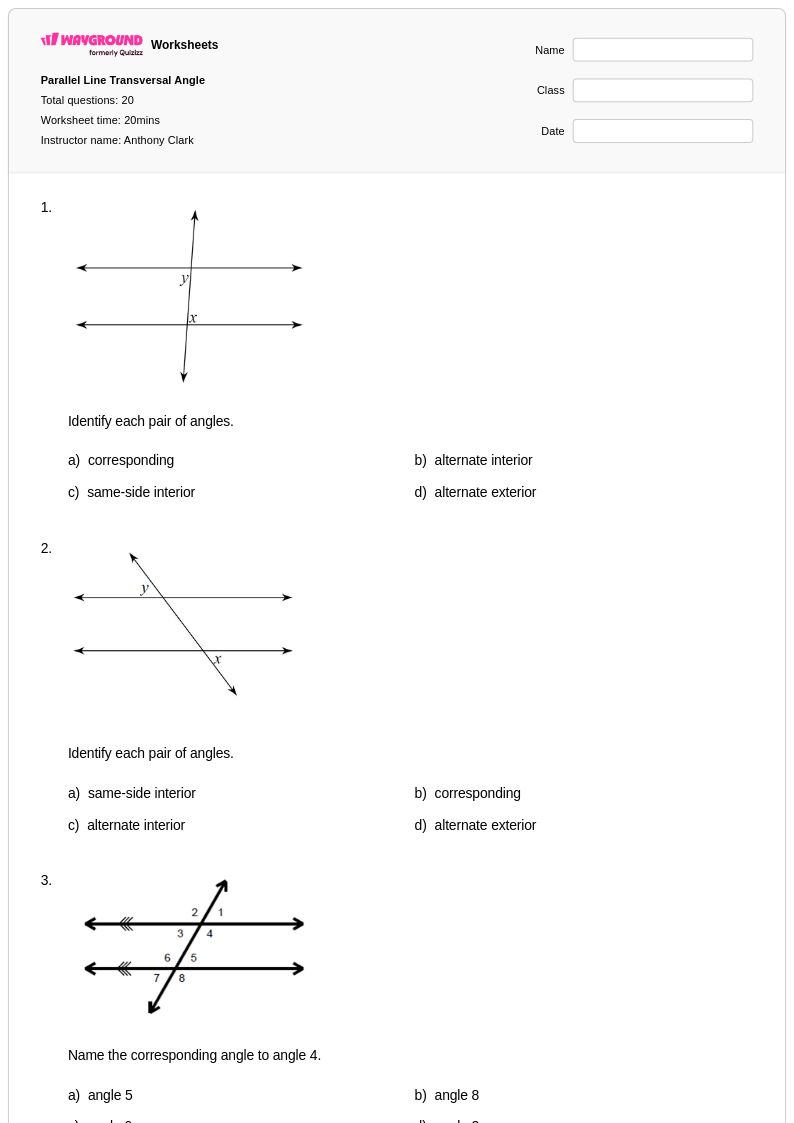
20 คิว
8th - Uni

15 คิว
8th
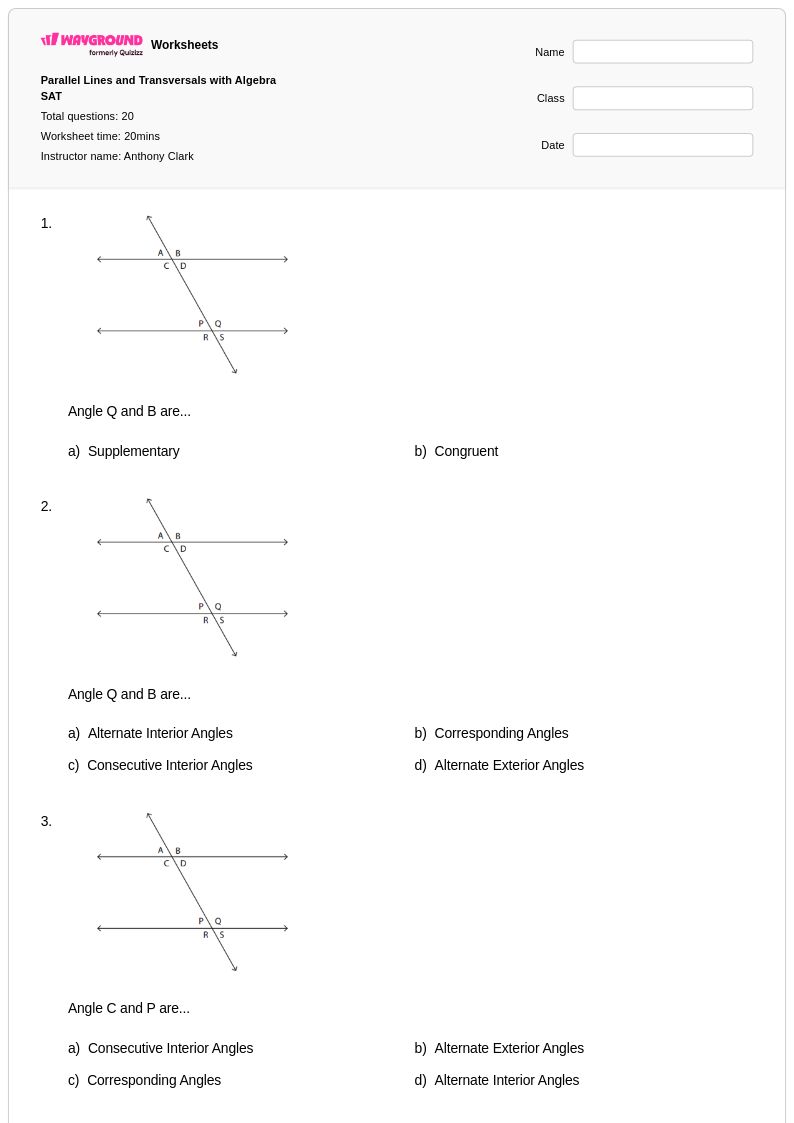
20 คิว
8th - Uni
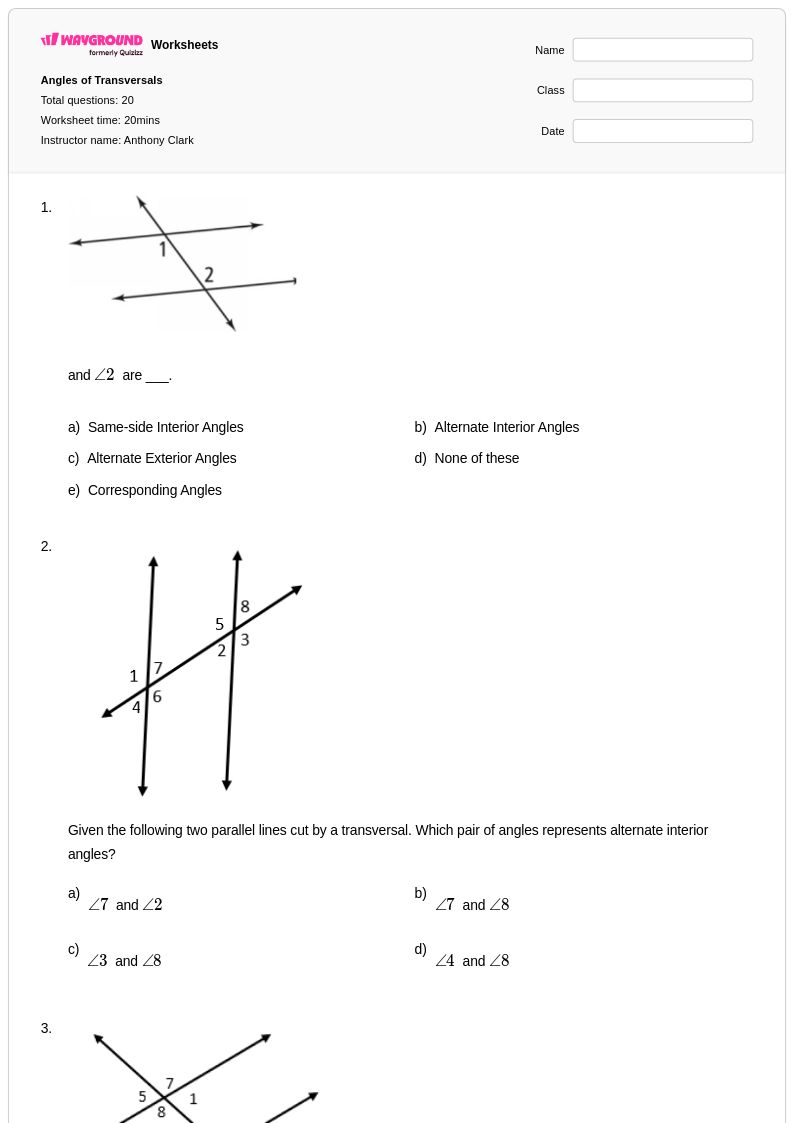
20 คิว
8th - Uni

51 คิว
8th
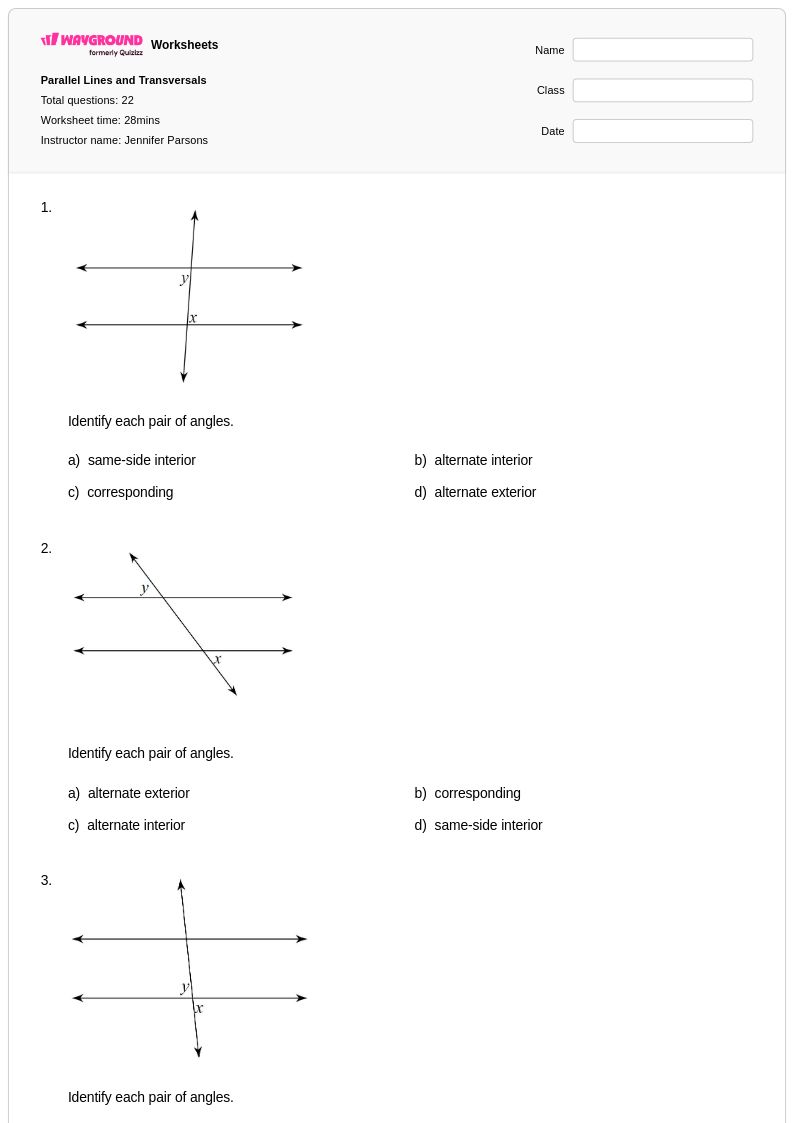
22 คิว
8th
20 คิว
8th - Uni
20 คิว
8th - Uni
22 คิว
8th
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 8
สำรวจแผ่นงาน เส้นตัดขวางของเส้นขนาน ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 8
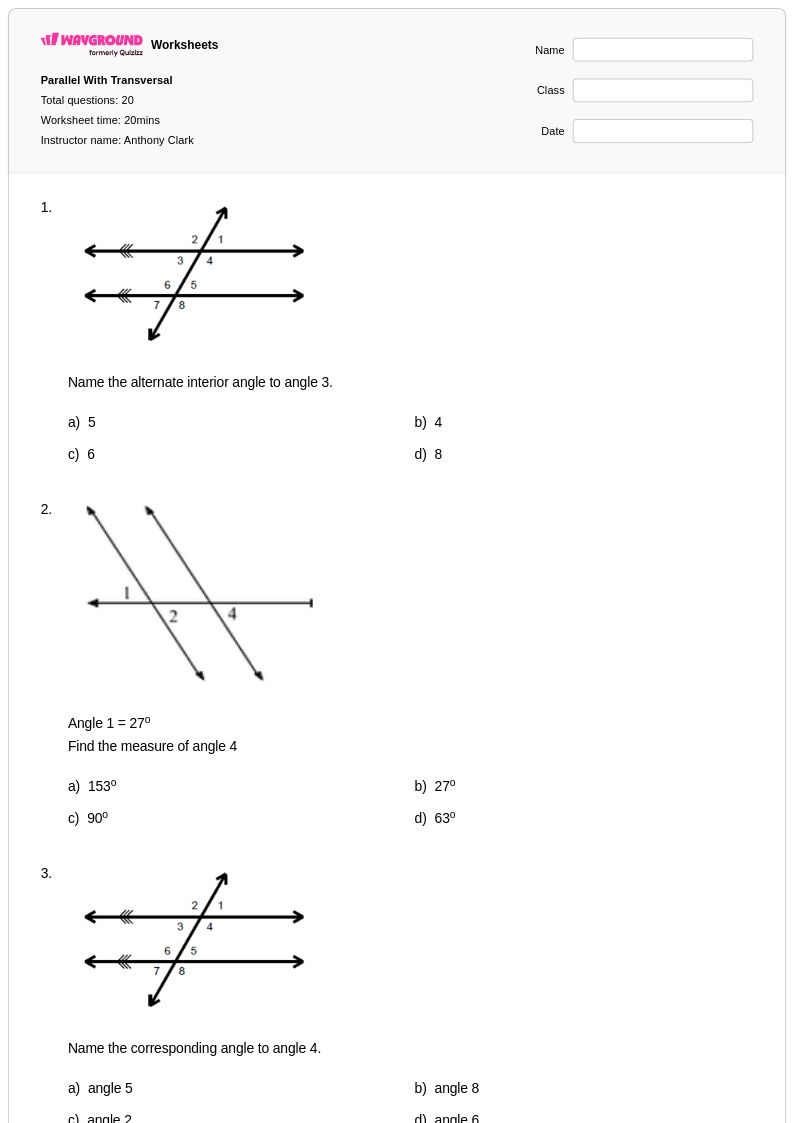
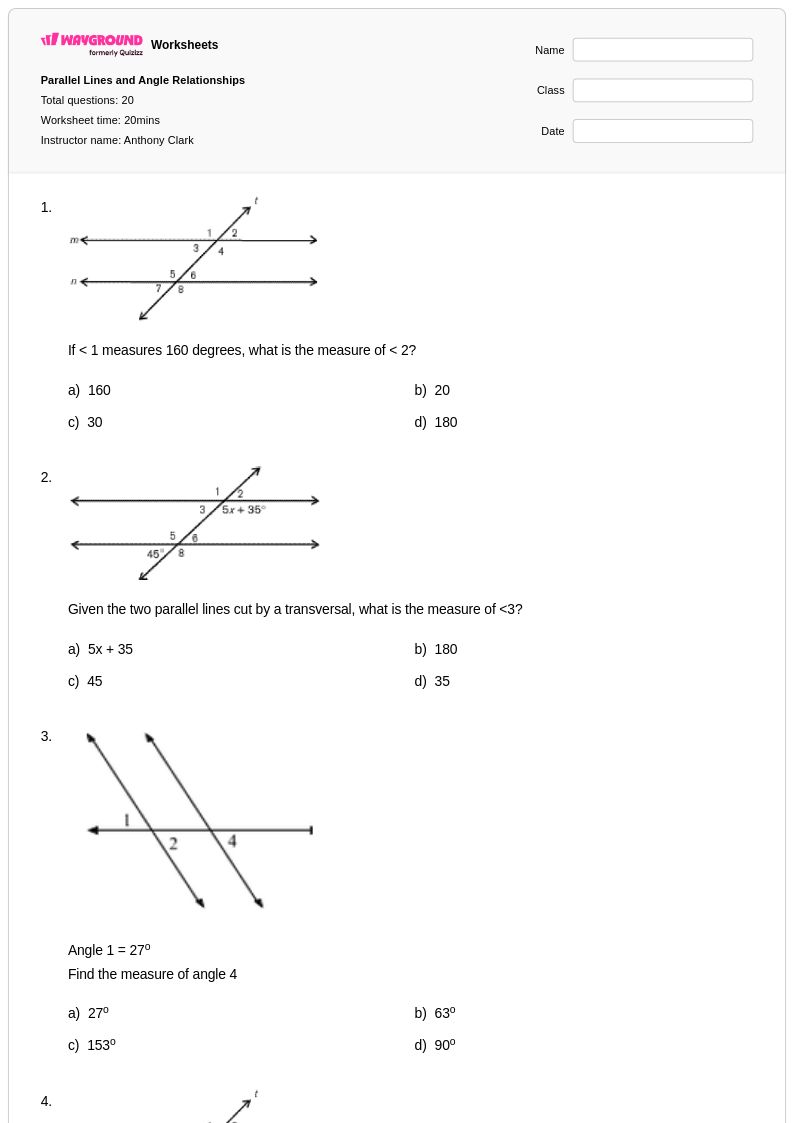
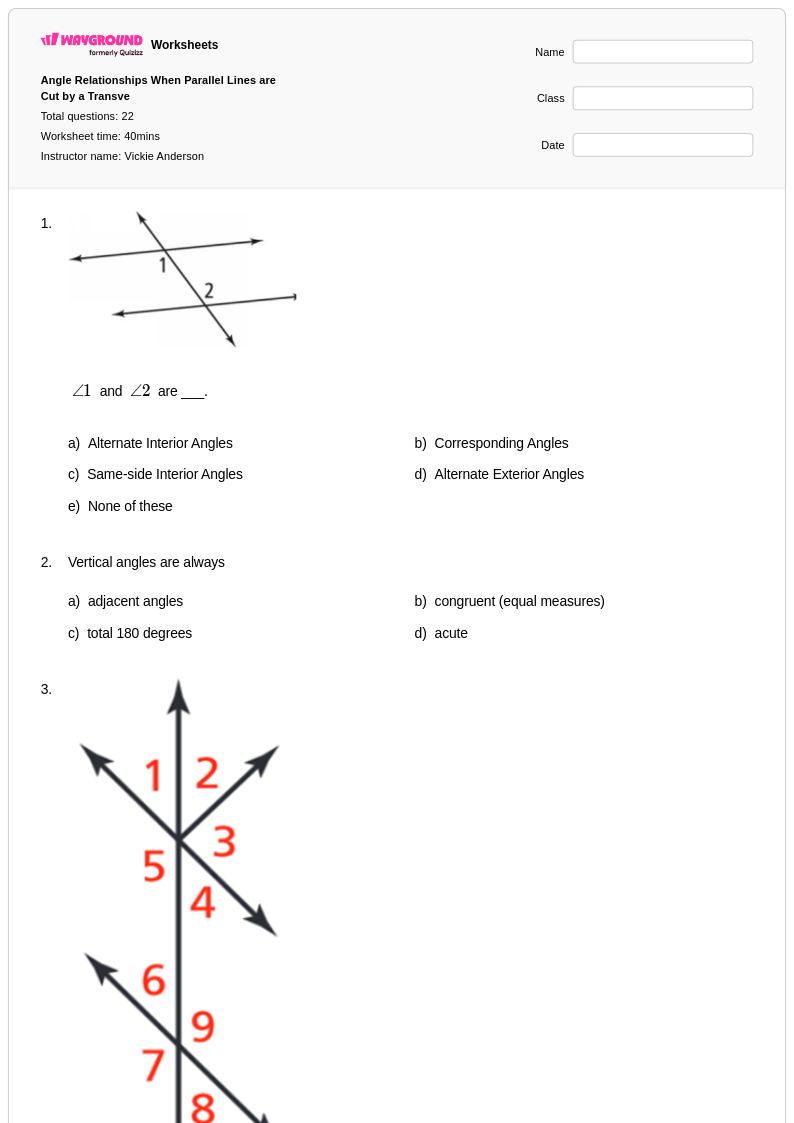
แบบฝึกหัดเรื่องเส้นตัดขวางตัดเส้นขนานสำหรับนักเรียนชั้น ม.2 จาก Wayground (เดิมคือ Quizizz) ให้แบบฝึกหัดที่ครอบคลุมเกี่ยวกับแนวคิดพื้นฐานที่สุดอย่างหนึ่งของเรขาคณิต แบบฝึกหัดที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยเสริมสร้างความสามารถของนักเรียนในการระบุและคำนวณความสัมพันธ์ของมุมเมื่อเส้นตัดขวางตัดเส้นขนานสองเส้น รวมถึงมุมที่สมนัยกัน มุมภายในสลับ มุมภายนอกสลับ และมุมภายในร่วม นักเรียนจะได้ฝึกฝนผ่านโจทย์ปัญหาที่ช่วยสร้างความเชี่ยวชาญในการประยุกต์ใช้ทฤษฎีบทเกี่ยวกับมุม การหาค่ามุมที่ไม่ทราบค่า และการจดจำรูปแบบทางเรขาคณิตในบริบทของโลกแห่งความเป็นจริง แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียด และสามารถดาวน์โหลดได้ฟรีในรูปแบบ PDF ทำให้ครูผู้สอนสามารถบูรณาการการฝึกฝนความสัมพันธ์ของมุมอย่างเป็นระบบเข้ากับหลักสูตรคณิตศาสตร์ได้อย่างง่ายดาย
Wayground (เดิมคือ Quizizz) ช่วยเสริมศักยภาพครูผู้สอนด้วยแหล่งข้อมูลนับล้านที่สร้างโดยครูผู้สอนโดยเฉพาะ ซึ่งมุ่งเน้นไปที่แนวคิดเรื่องเส้นตัดขวางและเส้นขนาน มีคุณสมบัติการค้นหาและการกรองที่มีประสิทธิภาพ ซึ่งสอดคล้องกับมาตรฐานคณิตศาสตร์ของรัฐสำหรับเรขาคณิตชั้น ม.2 เครื่องมือปรับแต่งของแพลตฟอร์มช่วยให้ครูสามารถปรับแต่งแบบฝึกหัดตามความต้องการของนักเรียนแต่ละคน ไม่ว่าจะเป็นการแก้ไขทักษะการระบุมุมขั้นพื้นฐาน หรือการเสริมสร้างความรู้ผ่านโจทย์คำนวณมุมที่ซับซ้อนหลายขั้นตอน ครูสามารถเปลี่ยนจากแบบฝึกหัด PDF ที่พิมพ์ได้สำหรับการใช้งานในห้องเรียนแบบดั้งเดิม ไปสู่รูปแบบดิจิทัลสำหรับสภาพแวดล้อมการเรียนรู้แบบโต้ตอบได้อย่างราบรื่น ในขณะที่คลังทรัพยากรที่ครอบคลุมช่วยสนับสนุนการวางแผนบทเรียนด้วยสื่อพร้อมใช้งานที่ตอบสนองต่อระดับทักษะที่แตกต่างกัน ความยืดหยุ่นนี้ช่วยให้ครูสามารถมอบโอกาสในการฝึกฝนที่ตรงเป้าหมาย ซึ่งช่วยเสริมสร้างเหตุผลทางเรขาคณิตและสร้างความเข้าใจพื้นฐานที่นักเรียนต้องการสำหรับแนวคิดเรขาคณิตขั้นสูง
