
25 คิว
7th - 9th
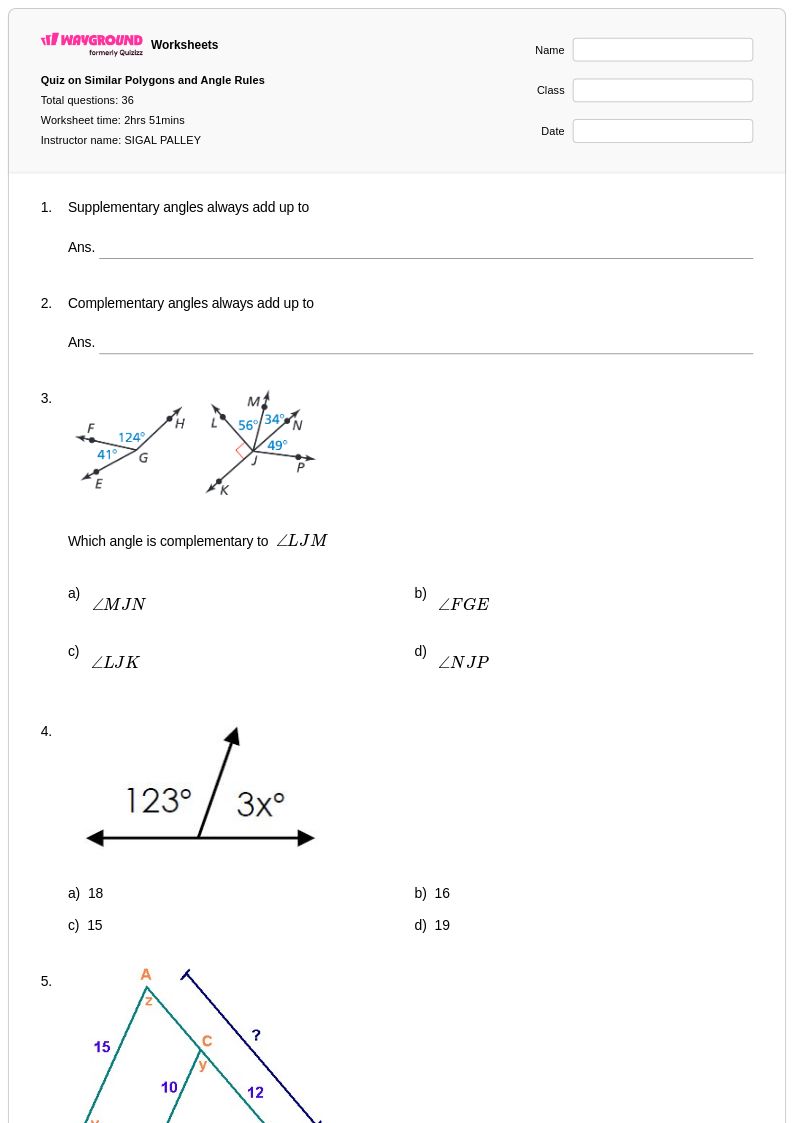
36 คิว
8th
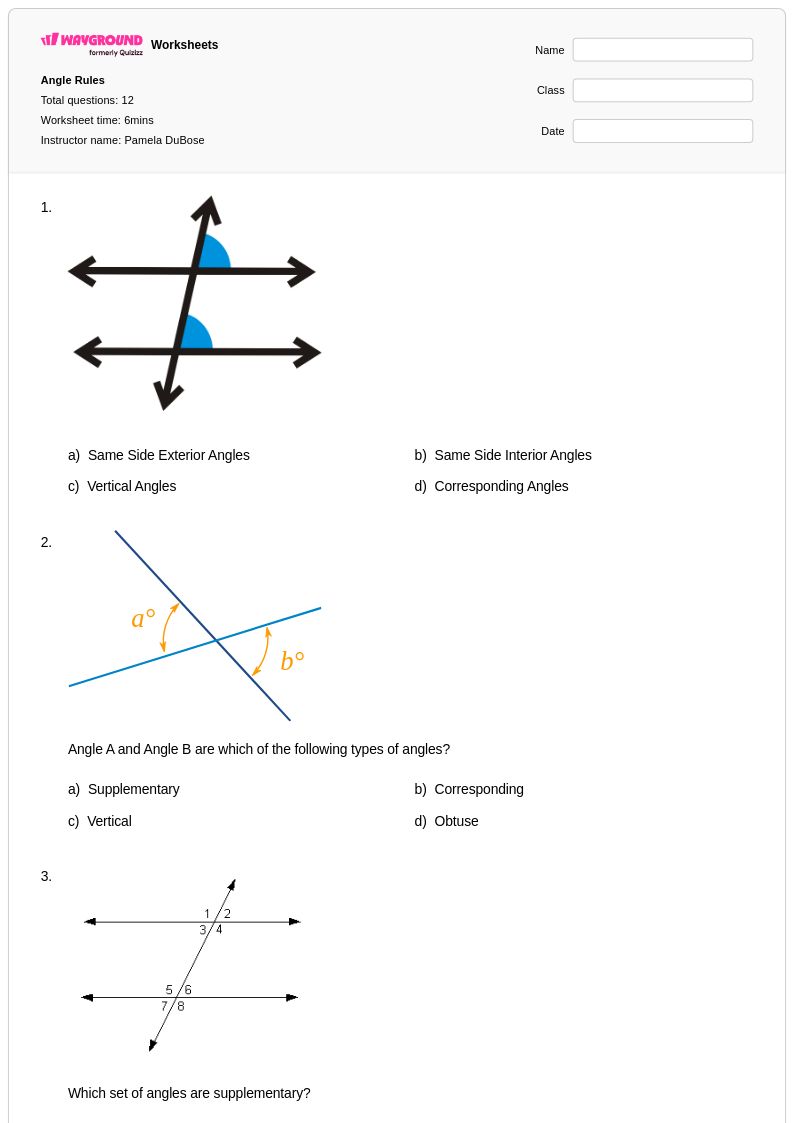
12 คิว
6th - 8th

12 คิว
8th
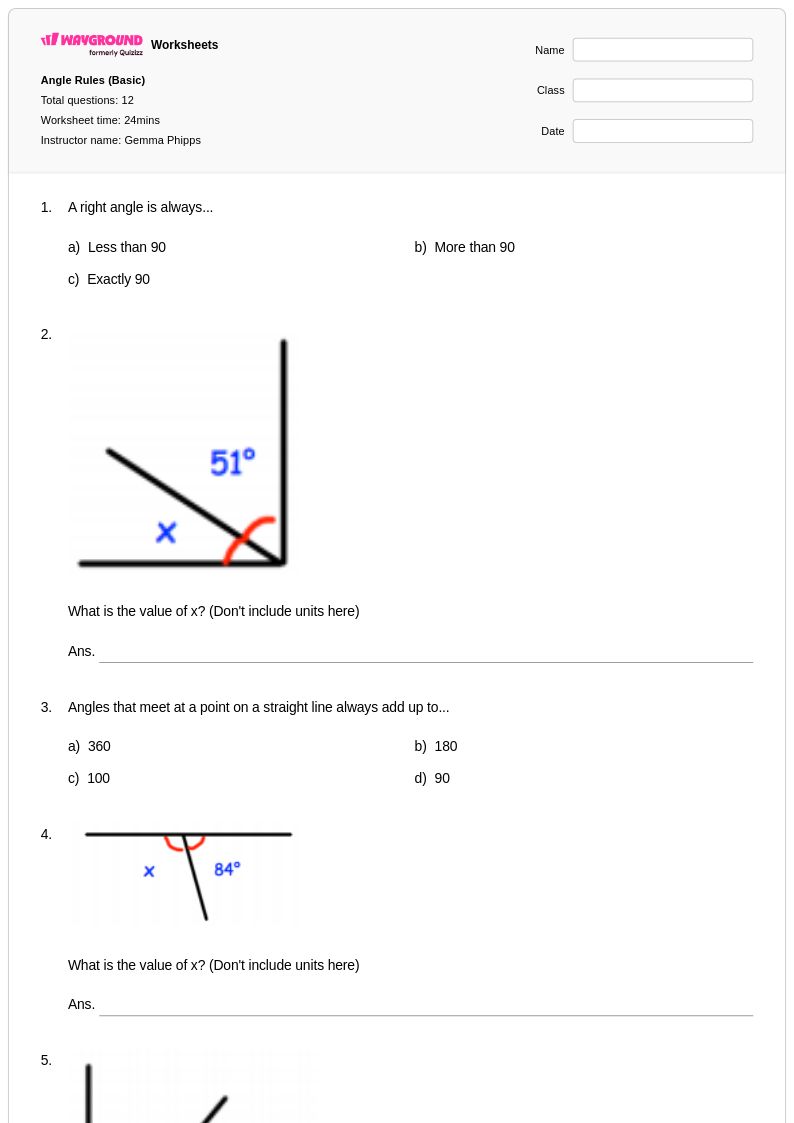
12 คิว
5th - 8th
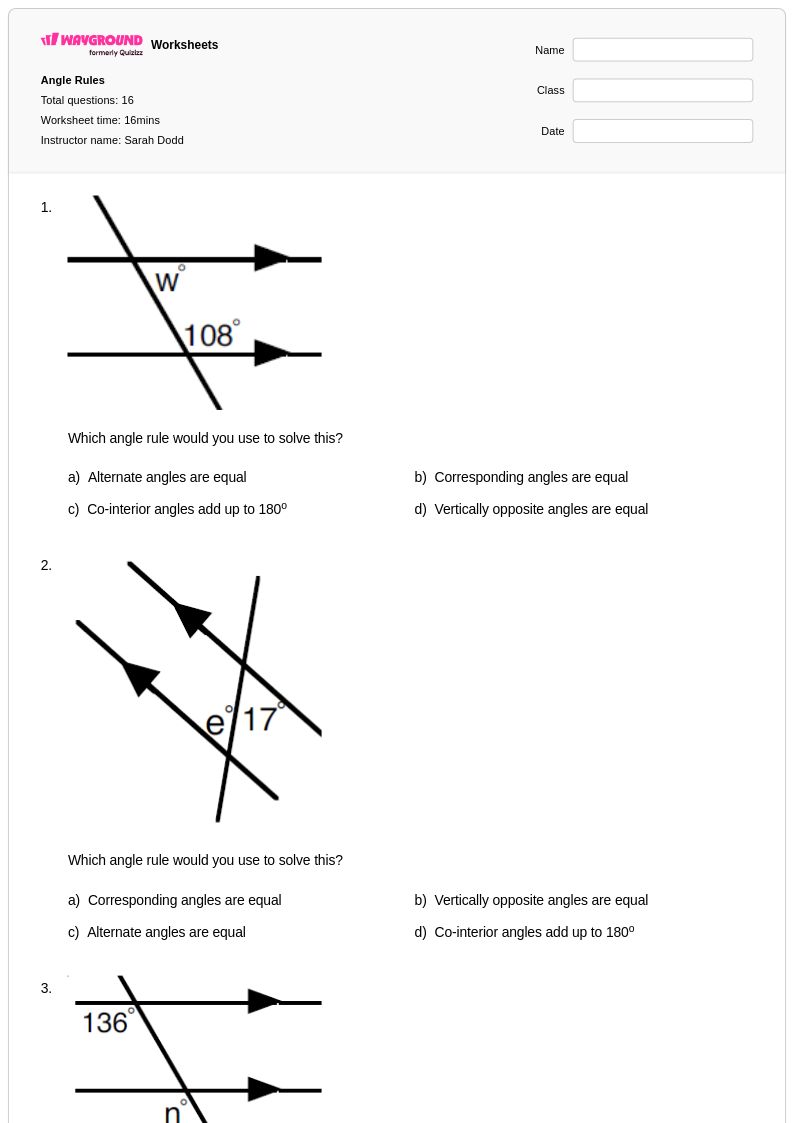
16 คิว
5th - 10th

19 คิว
7th - 12th
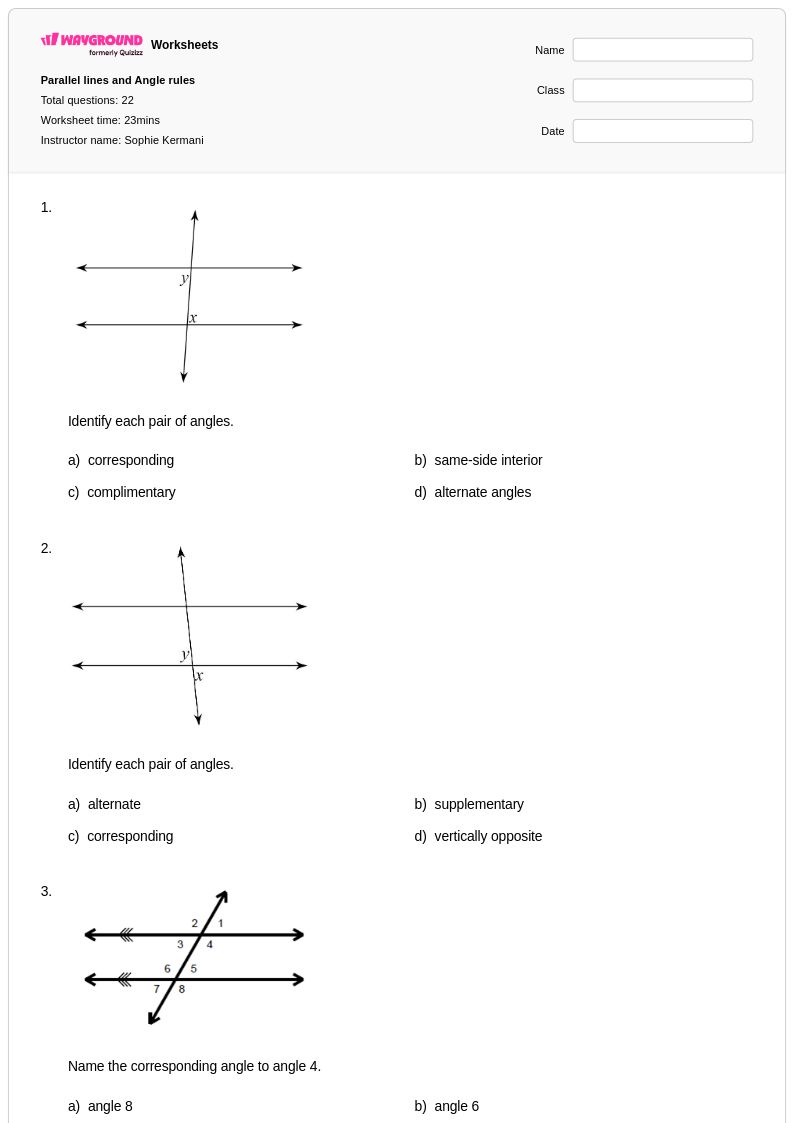
22 คิว
8th
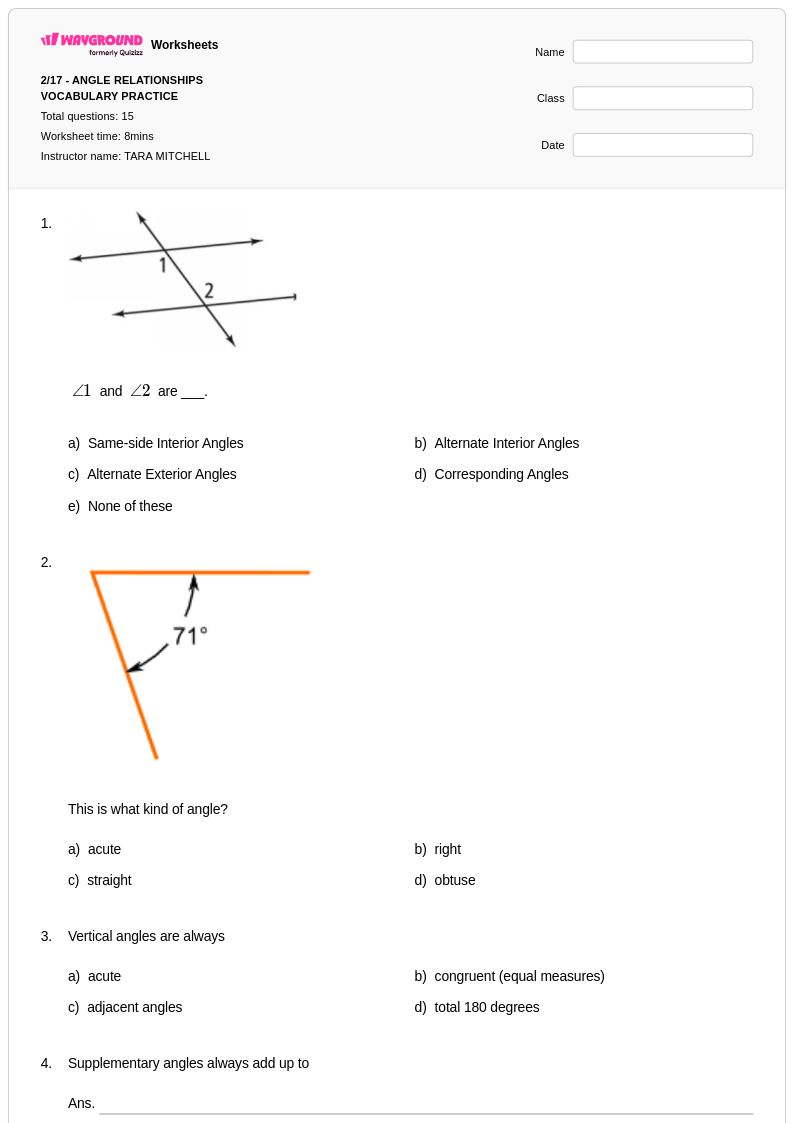
15 คิว
8th

23 คิว
8th
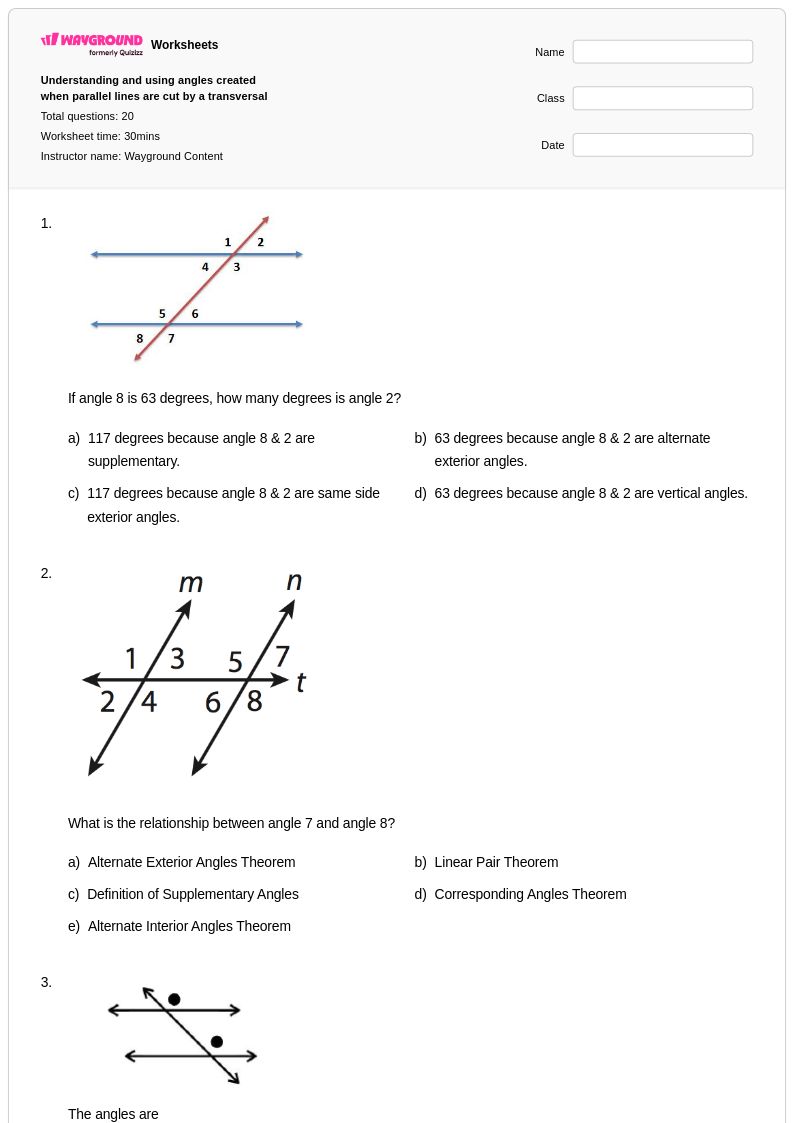
20 คิว
8th
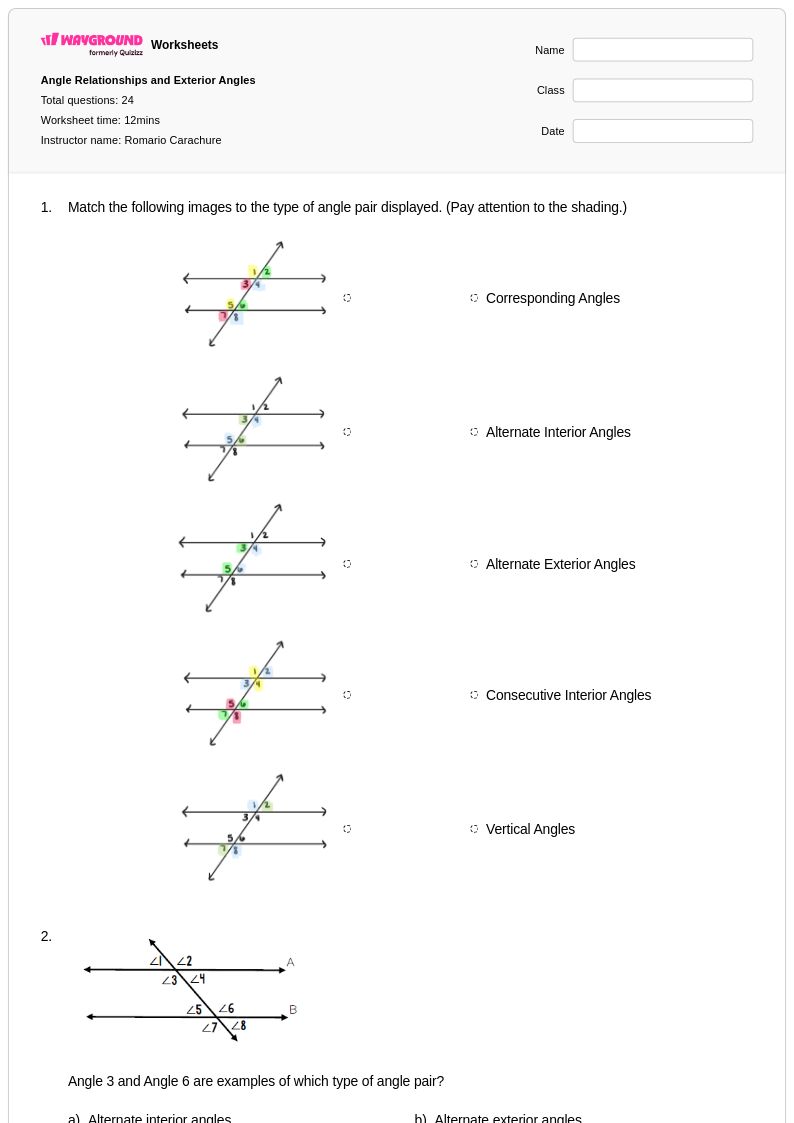
24 คิว
8th
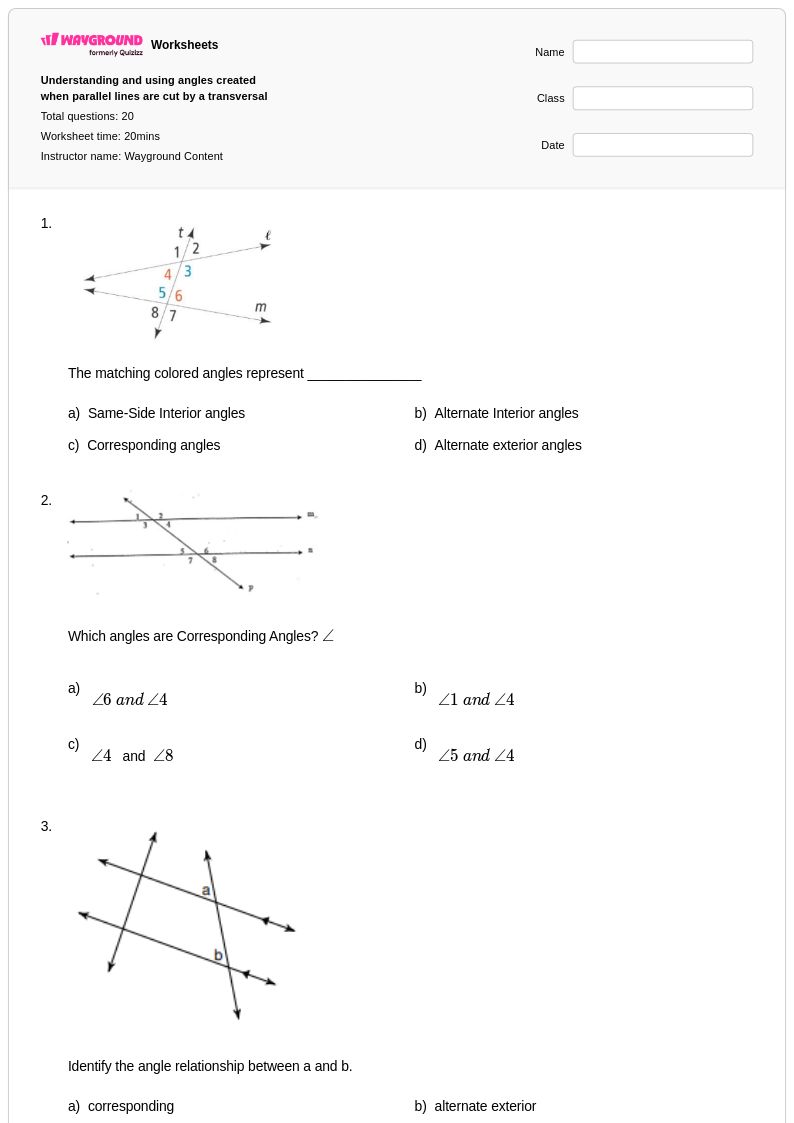
20 คิว
8th
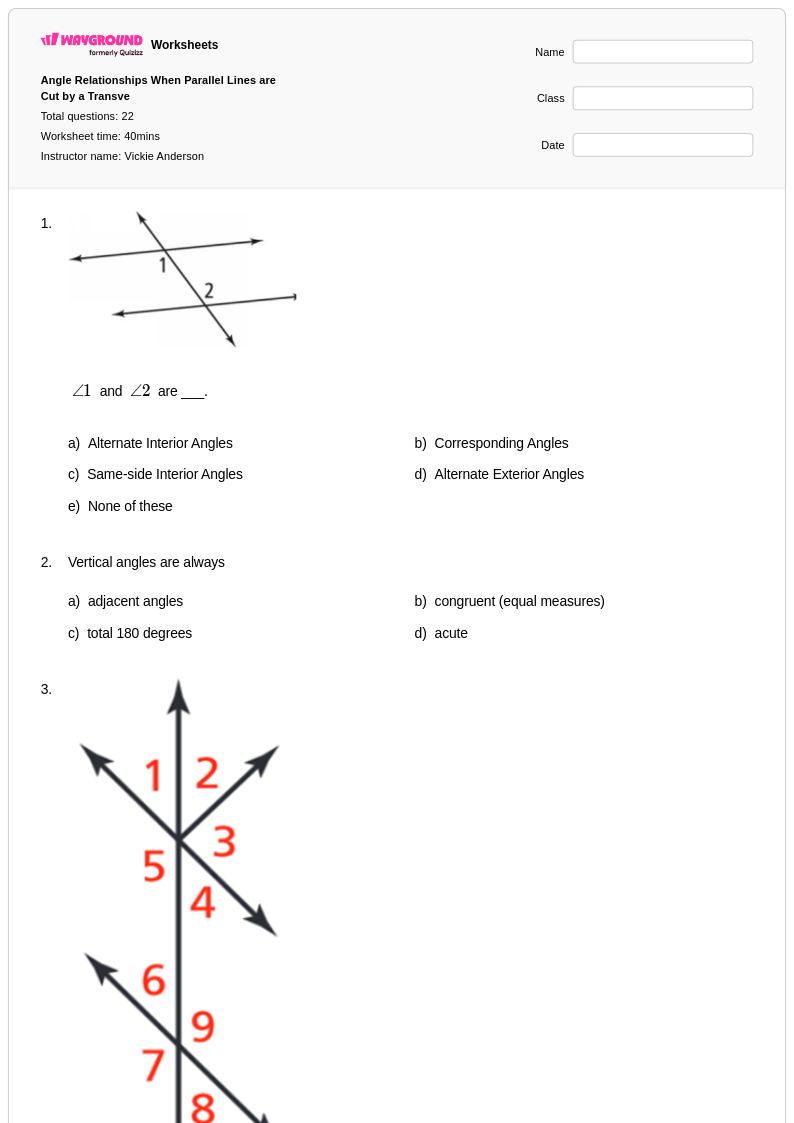
22 คิว
8th
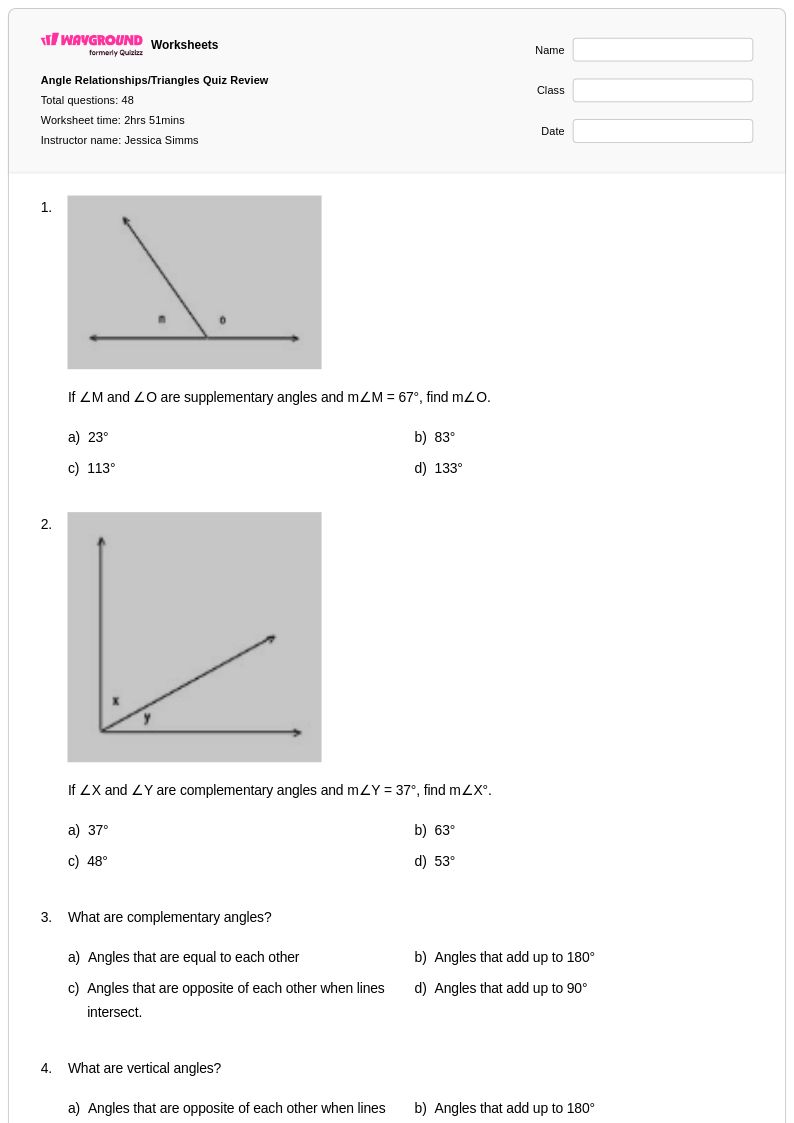
48 คิว
7th - 9th
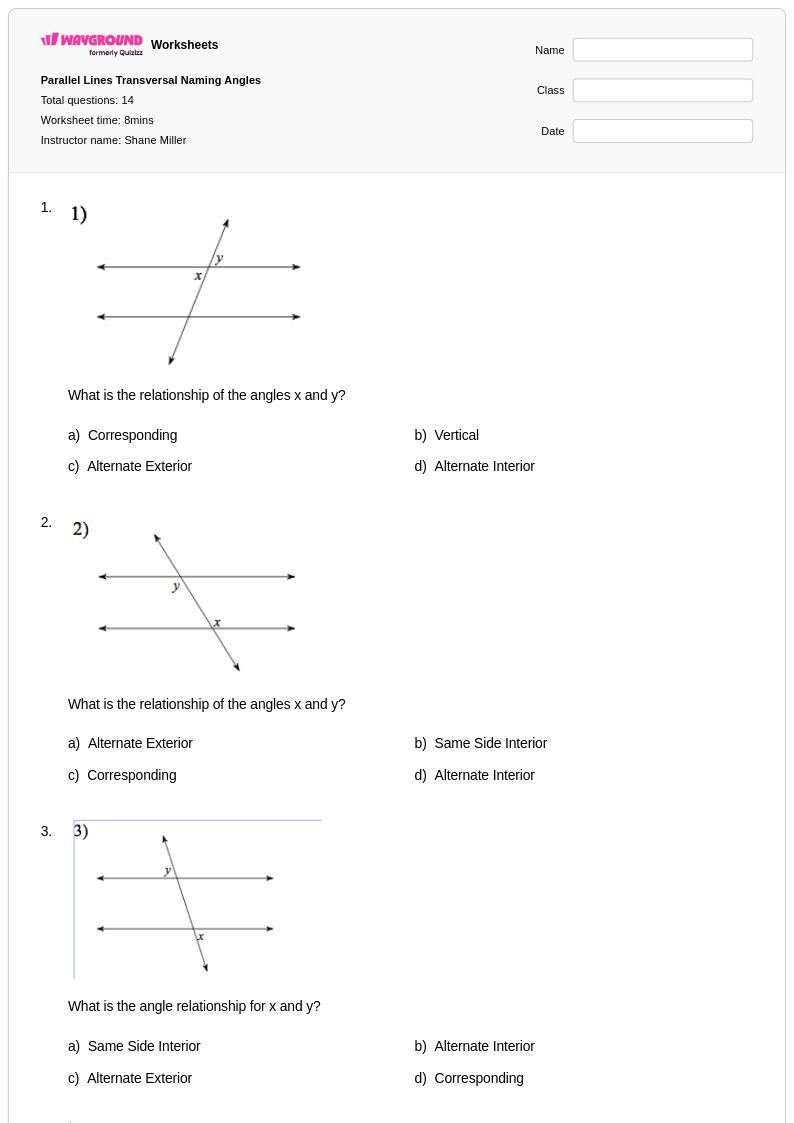
14 คิว
7th - 10th
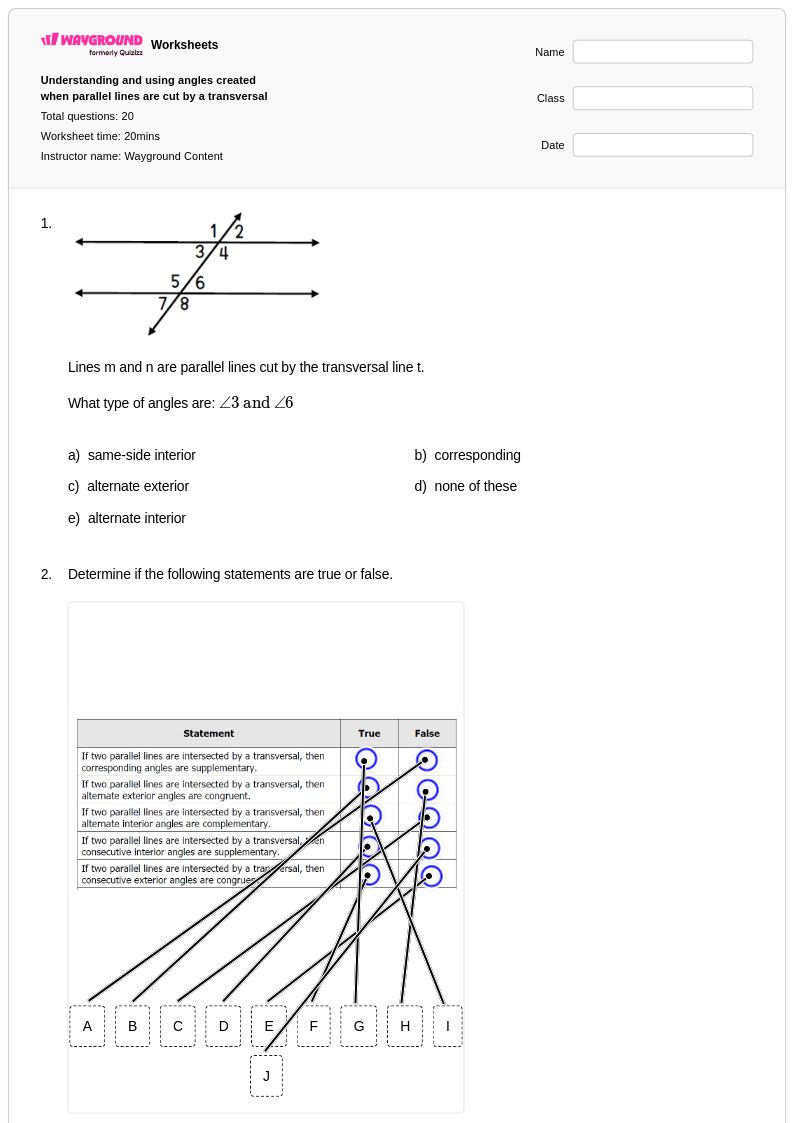
20 คิว
8th
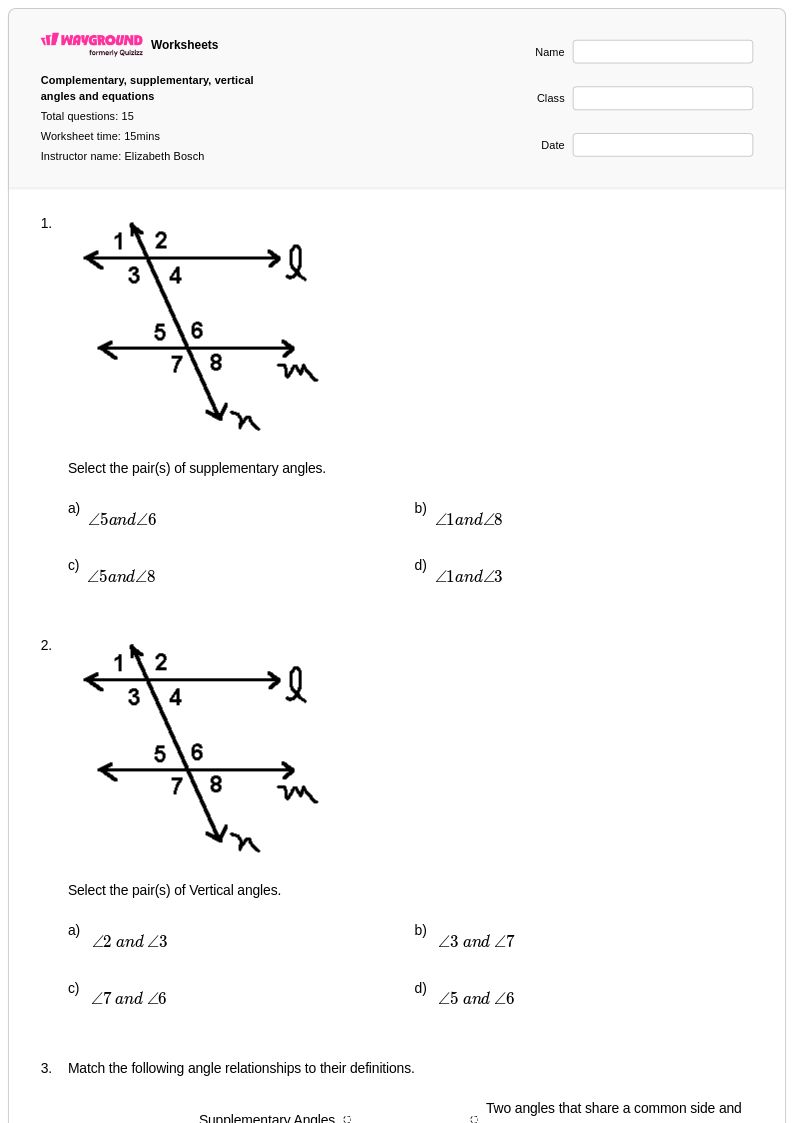
15 คิว
7th - Uni
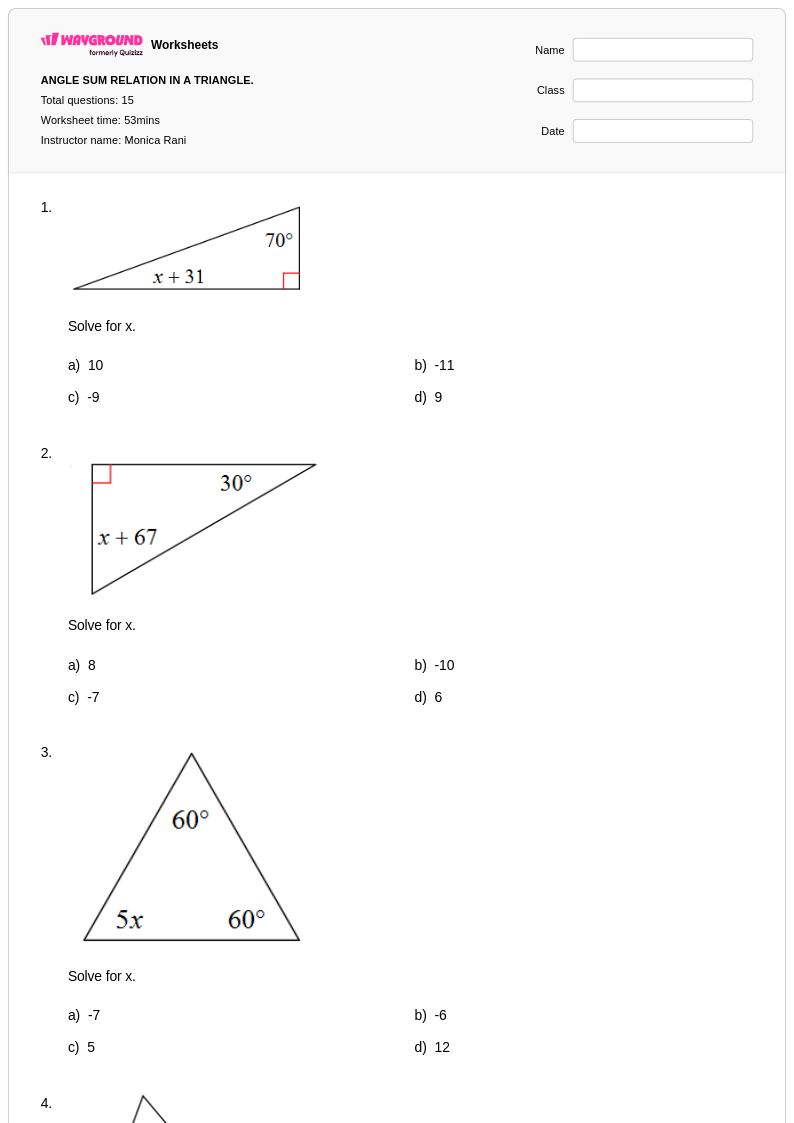
15 คิว
8th
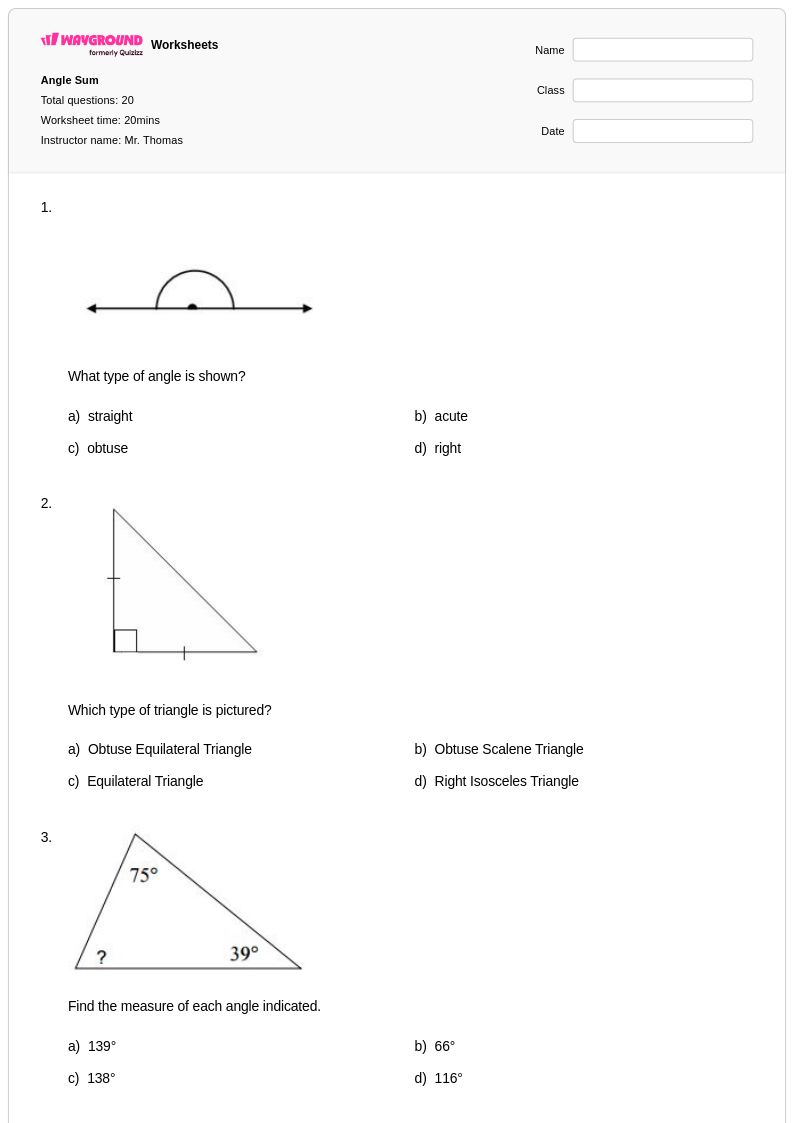
20 คิว
8th

16 คิว
8th
20 คิว
8th
20 คิว
8th

10 คิว
8th
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 8
สำรวจแผ่นงาน กฎของมุม ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 8
แบบฝึกหัดเรื่องกฎมุมสำหรับนักเรียนชั้น ม.2 จาก Wayground (เดิมชื่อ Quizizz) มอบโอกาสในการฝึกฝนอย่างครอบคลุมสำหรับนักเรียนที่ต้องการเรียนรู้ความสัมพันธ์ทางเรขาคณิตพื้นฐานและการประยุกต์ใช้ทฤษฎีบท แบบฝึกหัดเหล่านี้ได้รับการจัดทำขึ้นอย่างรอบคอบเพื่อเสริมสร้างทักษะที่สำคัญ เช่น การระบุมุมประกอบและมุมเสริม การทำงานกับมุมตรงข้าม การประยุกต์ใช้คุณสมบัติของเส้นขนานที่ถูกตัดด้วยเส้นตัดขวาง และการคำนวณขนาดมุมที่ไม่ทราบค่าในรูปทรงเรขาคณิตต่างๆ นักเรียนจะพัฒนาความเชี่ยวชาญในการจดจำความสัมพันธ์ของมุมภายในรูปสามเหลี่ยม รูปสี่เหลี่ยม และรูปหลายเหลี่ยมอื่นๆ พร้อมทั้งสร้างความสามารถในการใช้เหตุผลเชิงตรรกะผ่านการแก้ปัญหาทีละขั้นตอน แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียด และมีให้ใช้งานฟรีในรูปแบบไฟล์ PDF ที่สะดวก ช่วยให้ครูสามารถบูรณาการแบบฝึกหัดที่ตรงเป้าหมายเข้ากับการเรียนการสอนในชั้นเรียนและการบ้านได้อย่างราบรื่น
Wayground (เดิมชื่อ Quizizz) ช่วยเสริมศักยภาพให้แก่ครูผู้สอนด้วยแหล่งข้อมูลกฎมุมนับล้านรายการที่สร้างโดยครูผู้สอน เพื่อสนับสนุนความต้องการด้านการสอนและวัตถุประสงค์การเรียนรู้ที่หลากหลาย แพลตฟอร์มนี้มีระบบค้นหาและกรองข้อมูลที่มีประสิทธิภาพ ช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานหลักสูตรเฉพาะ และปรับระดับความยากง่ายให้เหมาะสมกับระดับทักษะต่างๆ ในห้องเรียนคณิตศาสตร์ ม.2 ได้อย่างรวดเร็ว แบบฝึกหัดเหล่านี้มีให้เลือกทั้งแบบพิมพ์ได้และแบบดิจิทัล รวมถึงไฟล์ PDF ที่ดาวน์โหลดได้ ซึ่งช่วยให้วางแผนการสอนได้อย่างยืดหยุ่นและรองรับสภาพแวดล้อมการเรียนรู้ที่แตกต่างกัน ครูสามารถปรับแต่งแหล่งข้อมูลที่มีอยู่ หรือสร้างสื่อใหม่เพื่อตอบสนองความต้องการของนักเรียนแต่ละคน ทำให้เครื่องมือเหล่านี้มีคุณค่าอย่างยิ่งสำหรับการแก้ไขปัญหาเฉพาะด้าน การเสริมสร้างทักษะ และกิจกรรมเสริมความรู้ที่ช่วยให้นักเรียนเข้าใจความสัมพันธ์ที่ซับซ้อนเกี่ยวกับการวัดมุมและคุณสมบัติทางเรขาคณิตได้ดียิ่งขึ้น
