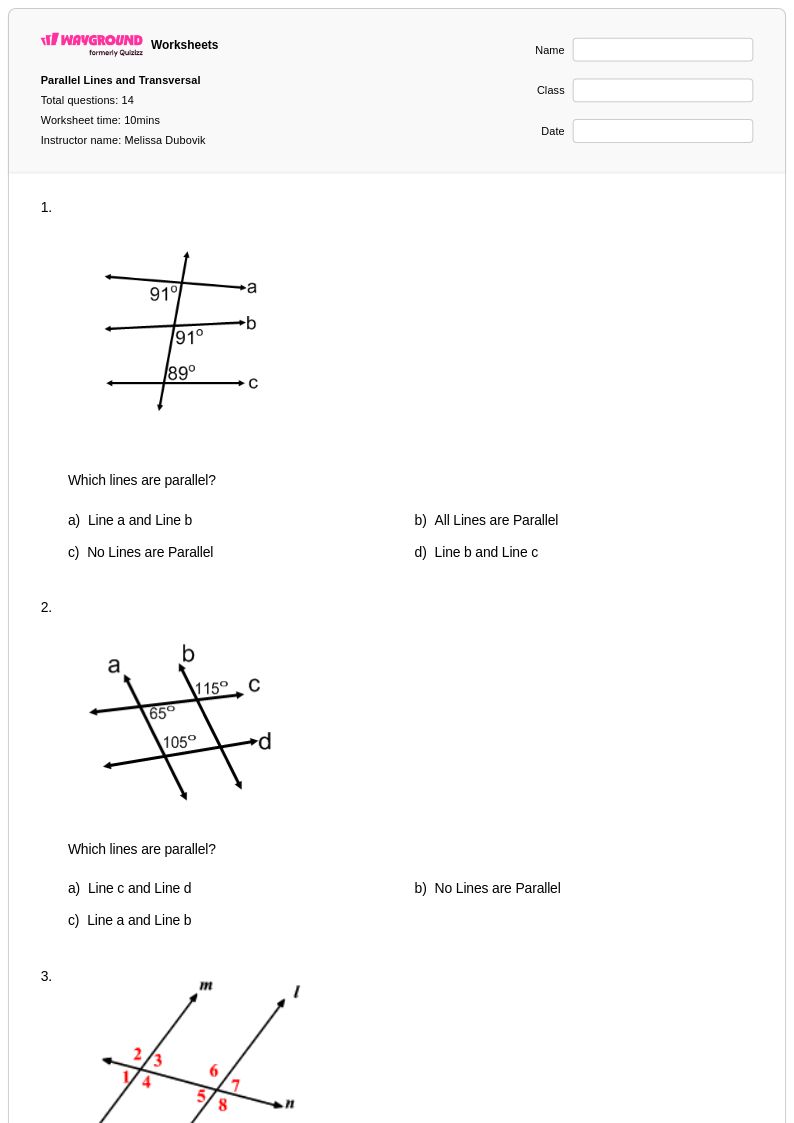
14 คิว
9th - 11th
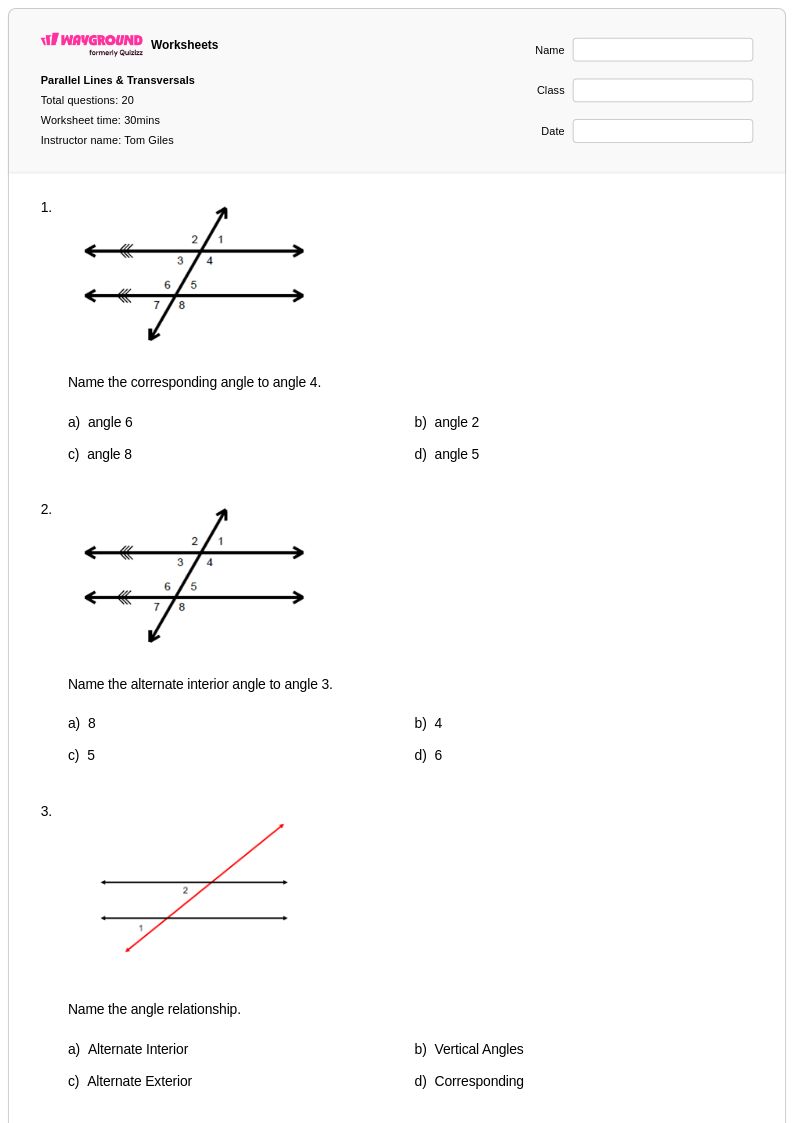
20 คิว
10th - 11th

10 คิว
8th - 11th
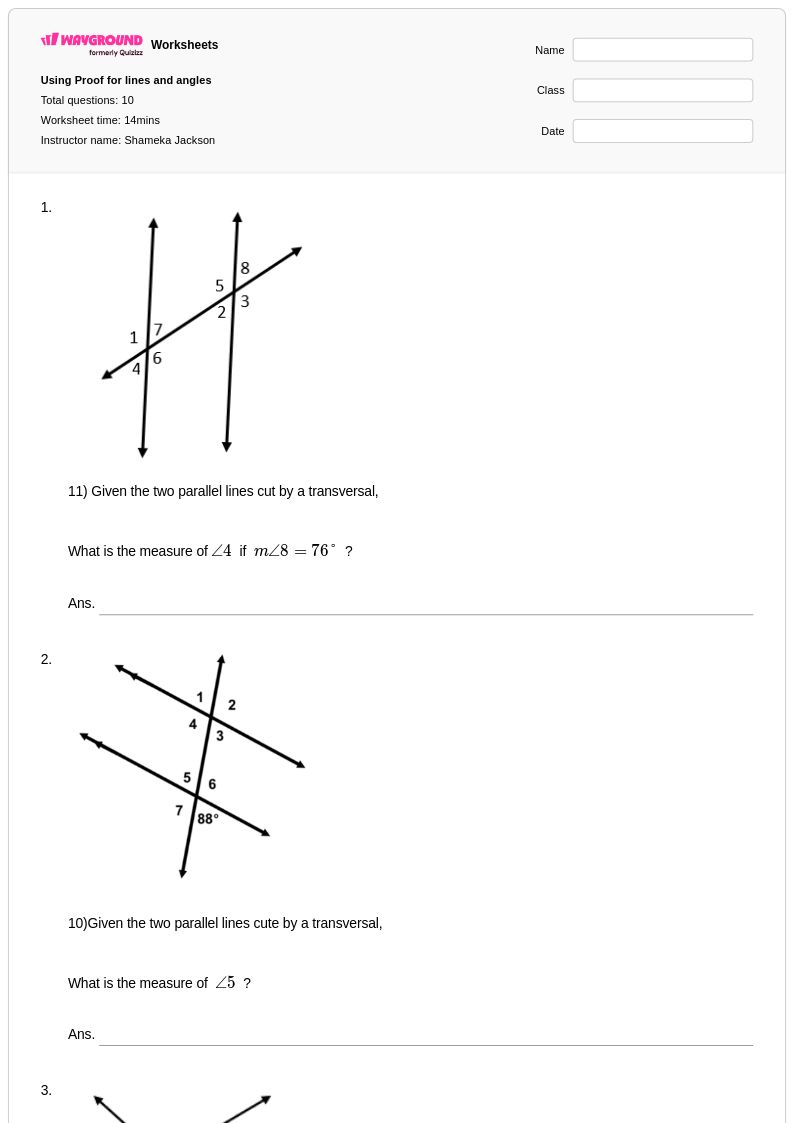
10 คิว
10th - 11th
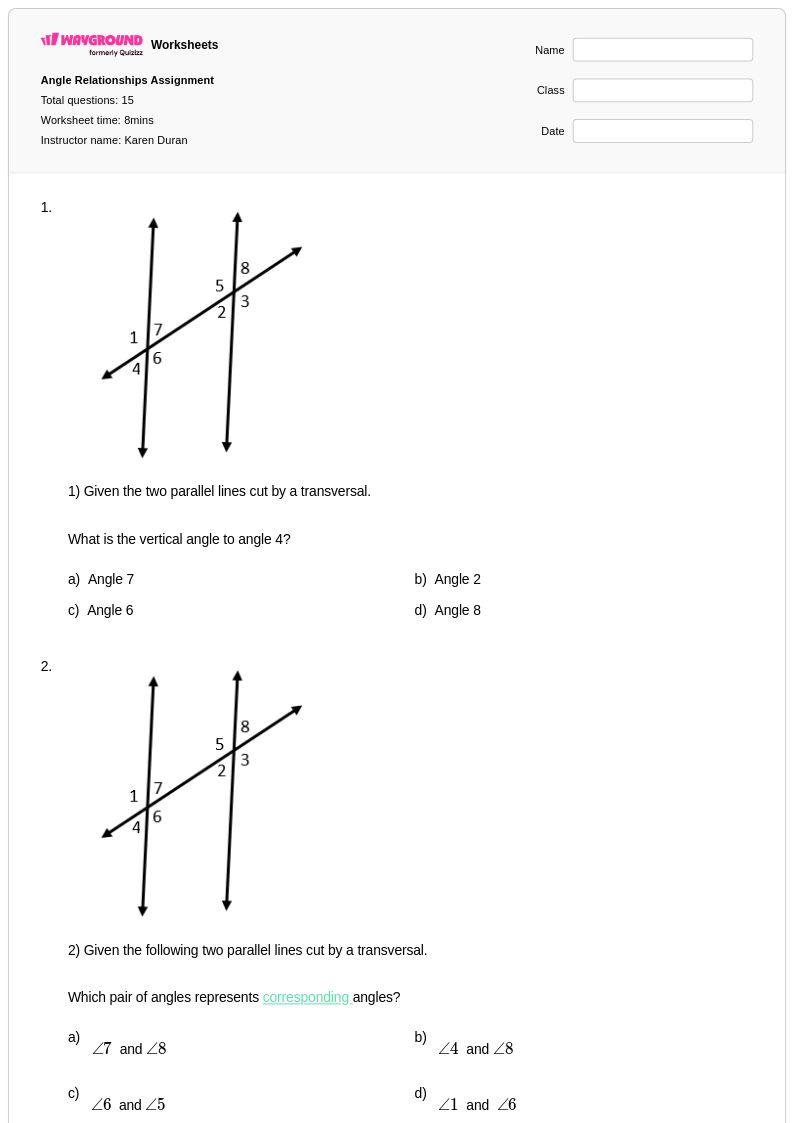
15 คิว
8th - 11th
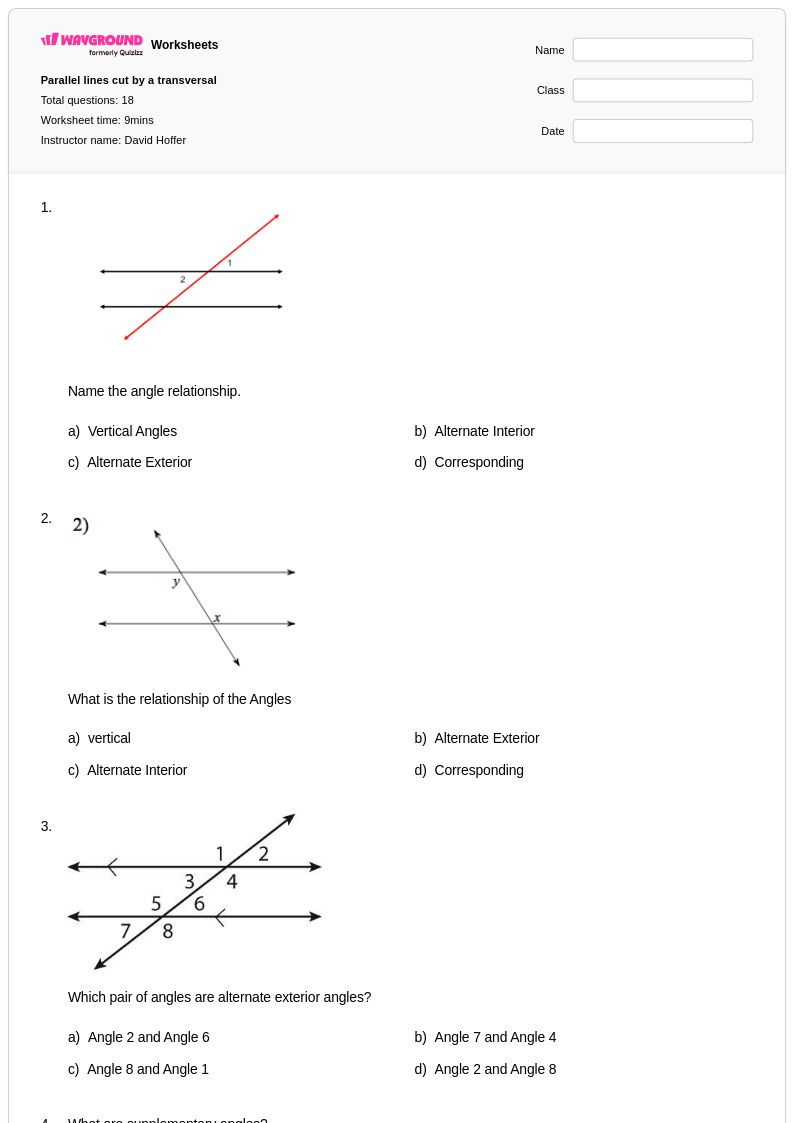
18 คิว
9th - 11th
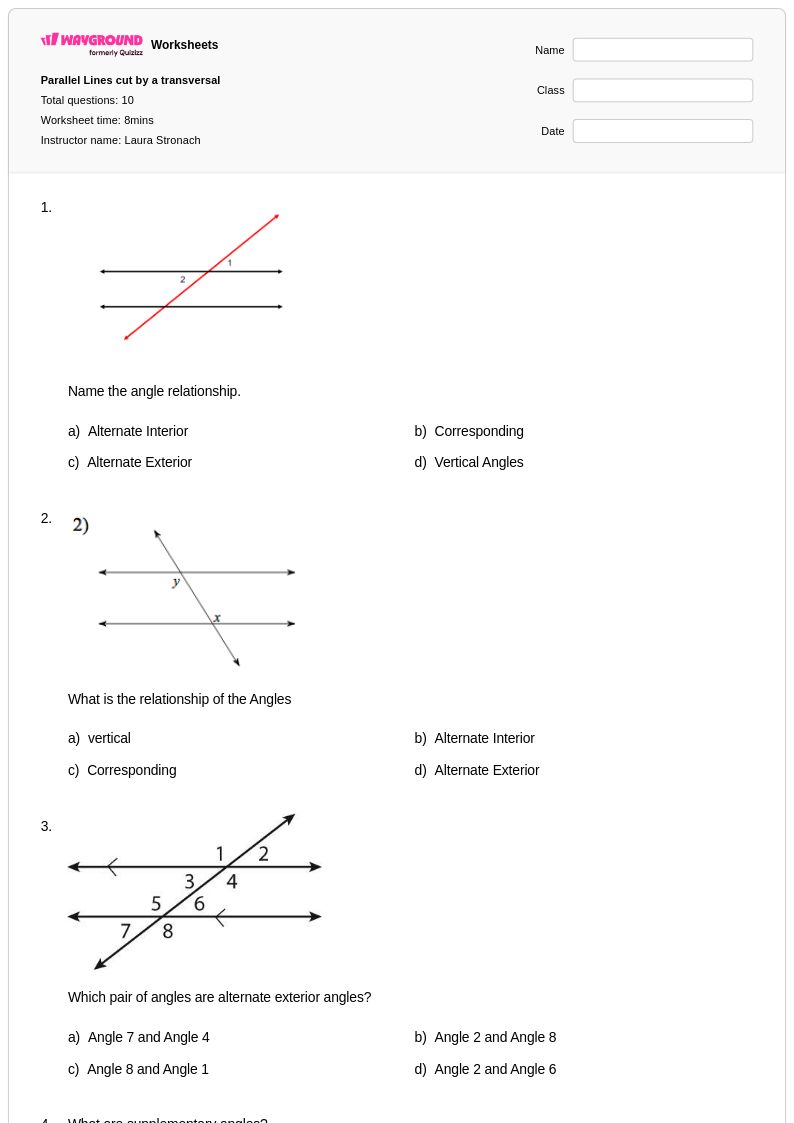
10 คิว
9th - 11th
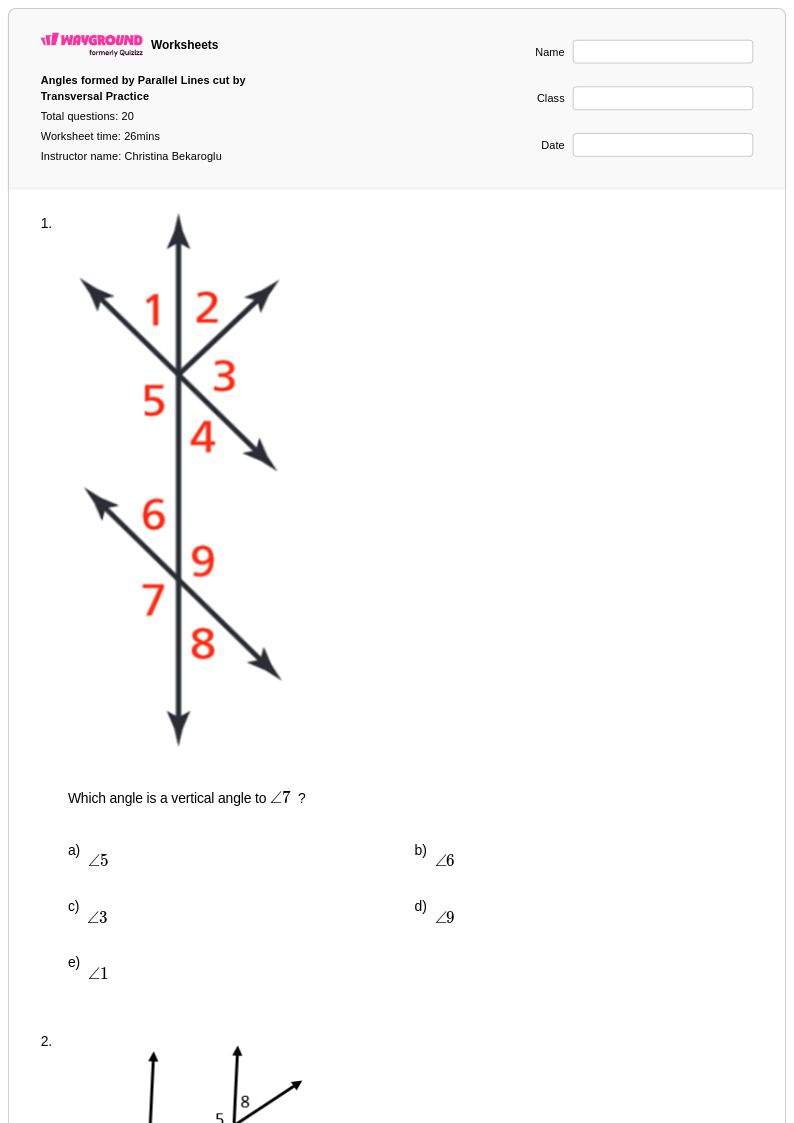
20 คิว
9th - 12th
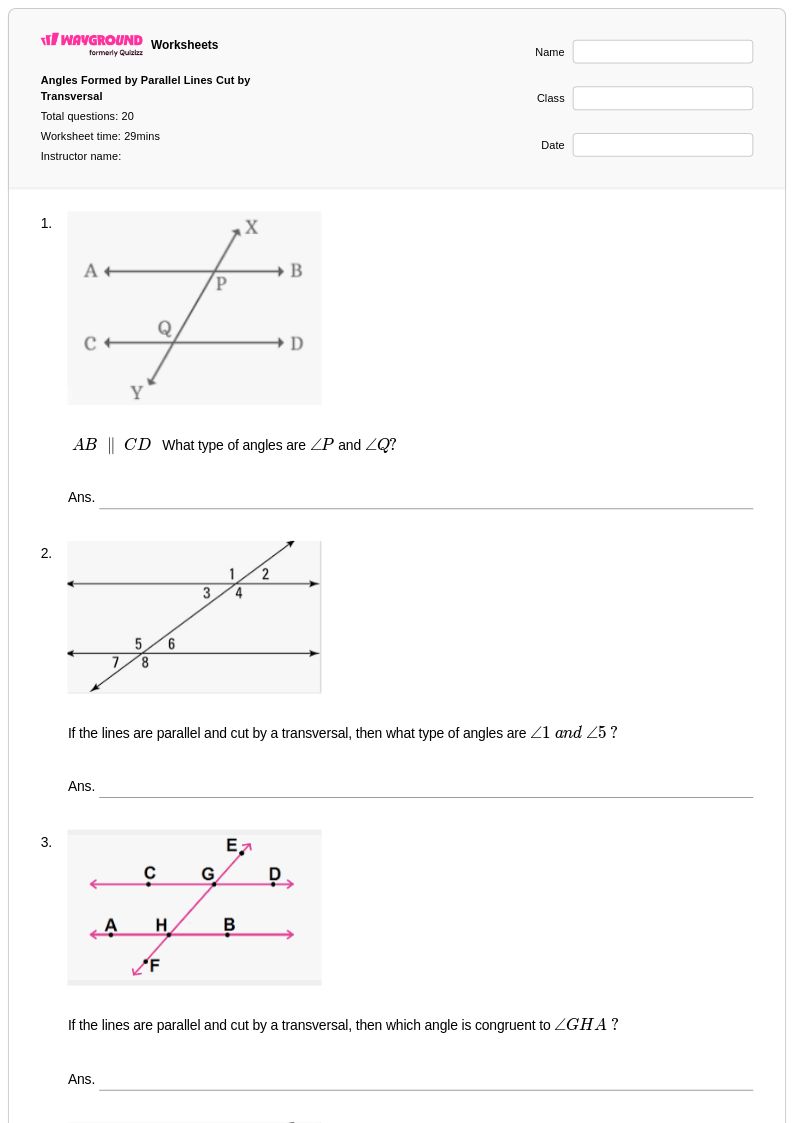
20 คิว
8th - 11th
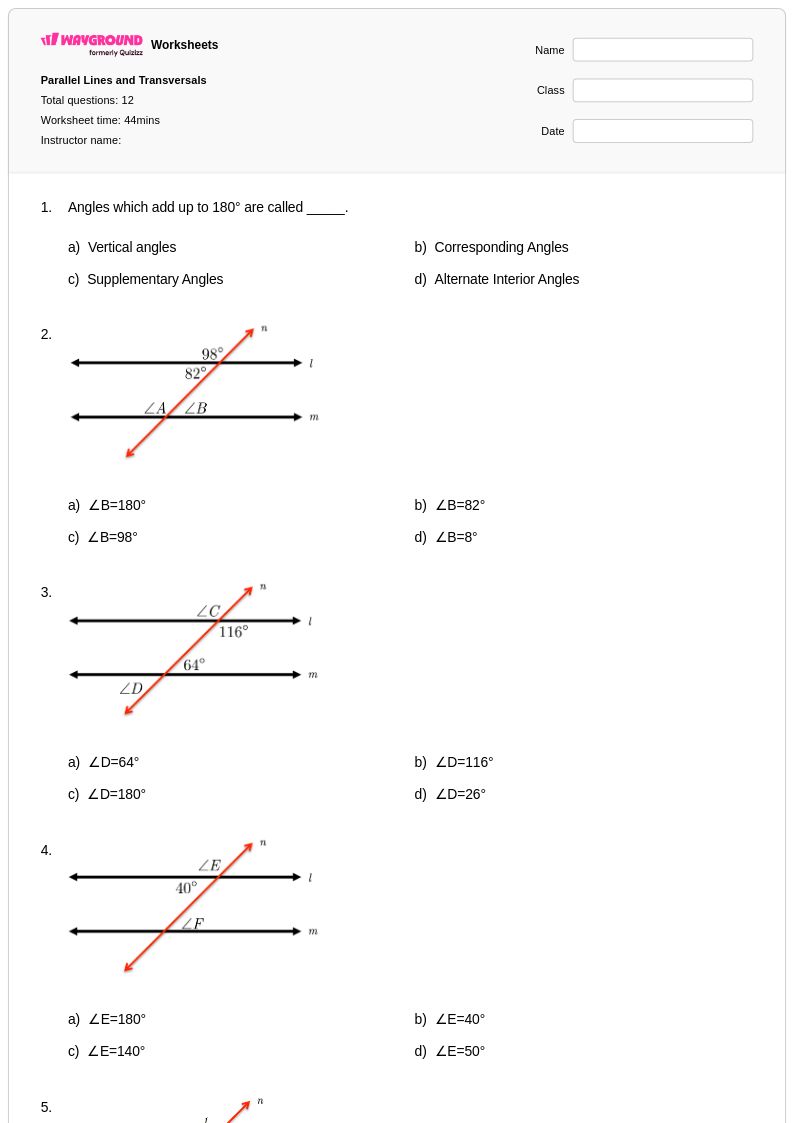
12 คิว
8th - 11th
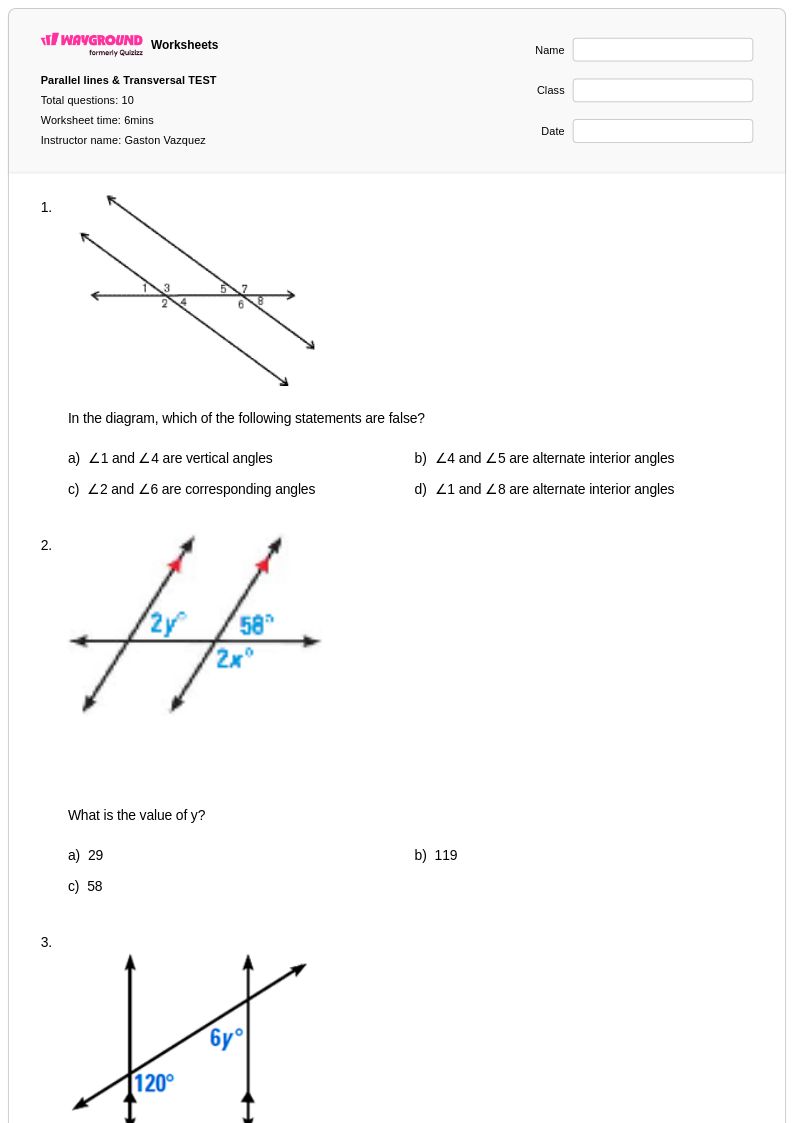
10 คิว
9th - 11th

20 คิว
11th
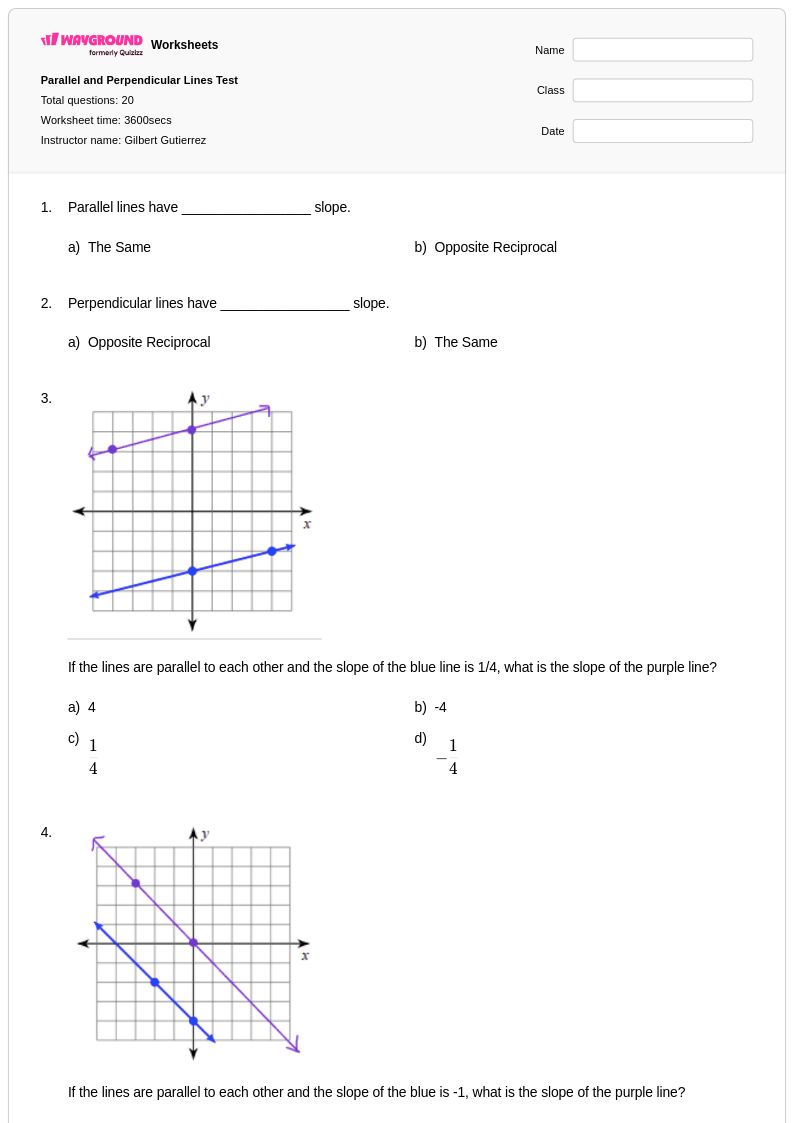
20 คิว
9th - 11th

23 คิว
9th - 11th
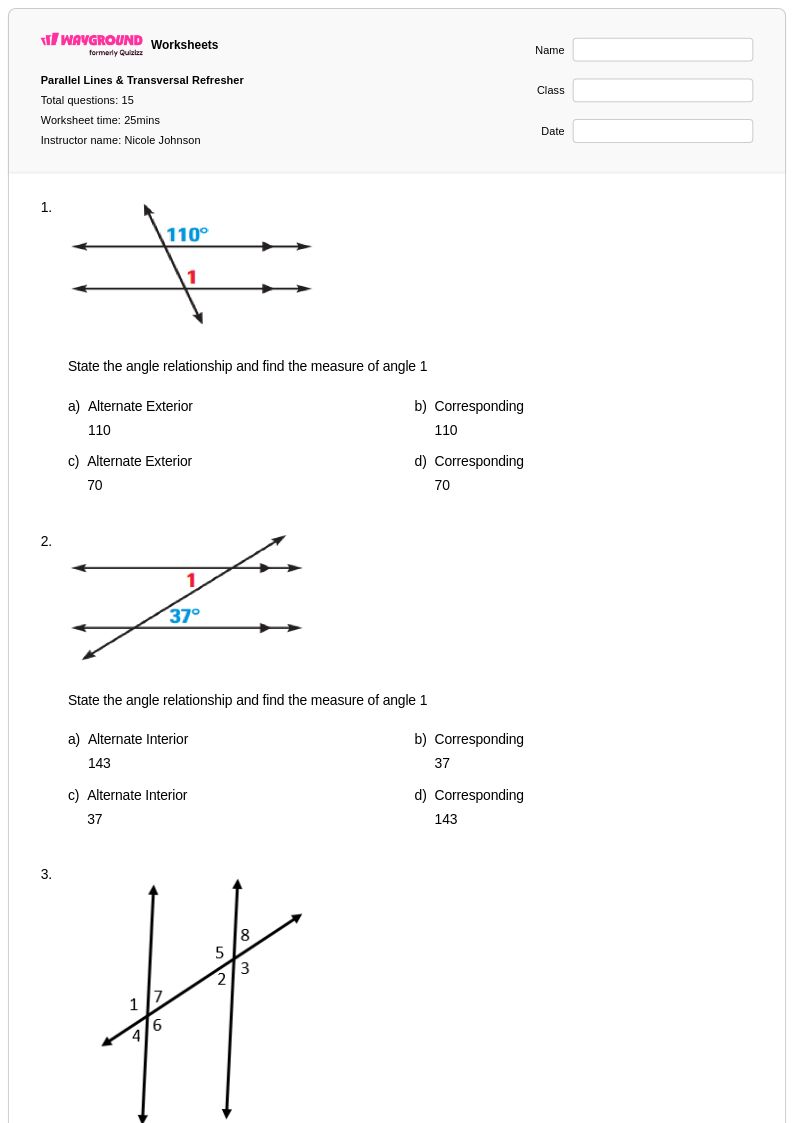
15 คิว
9th - 11th
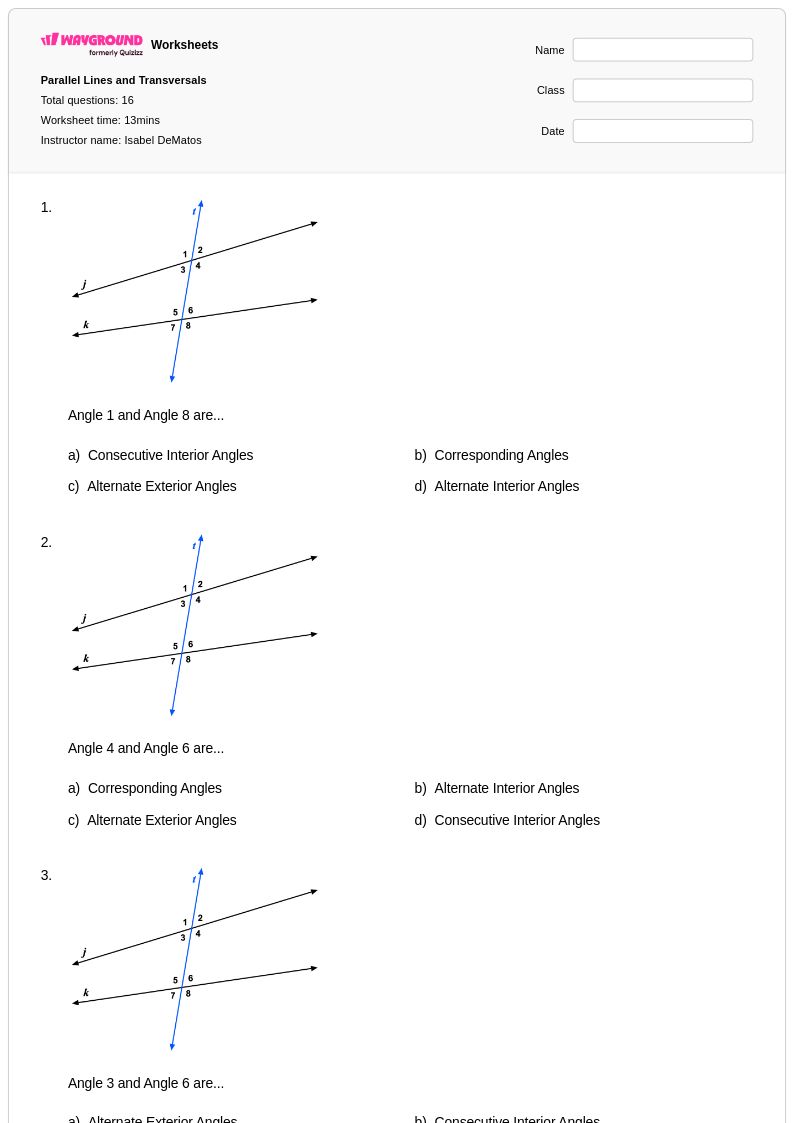
16 คิว
7th - 11th
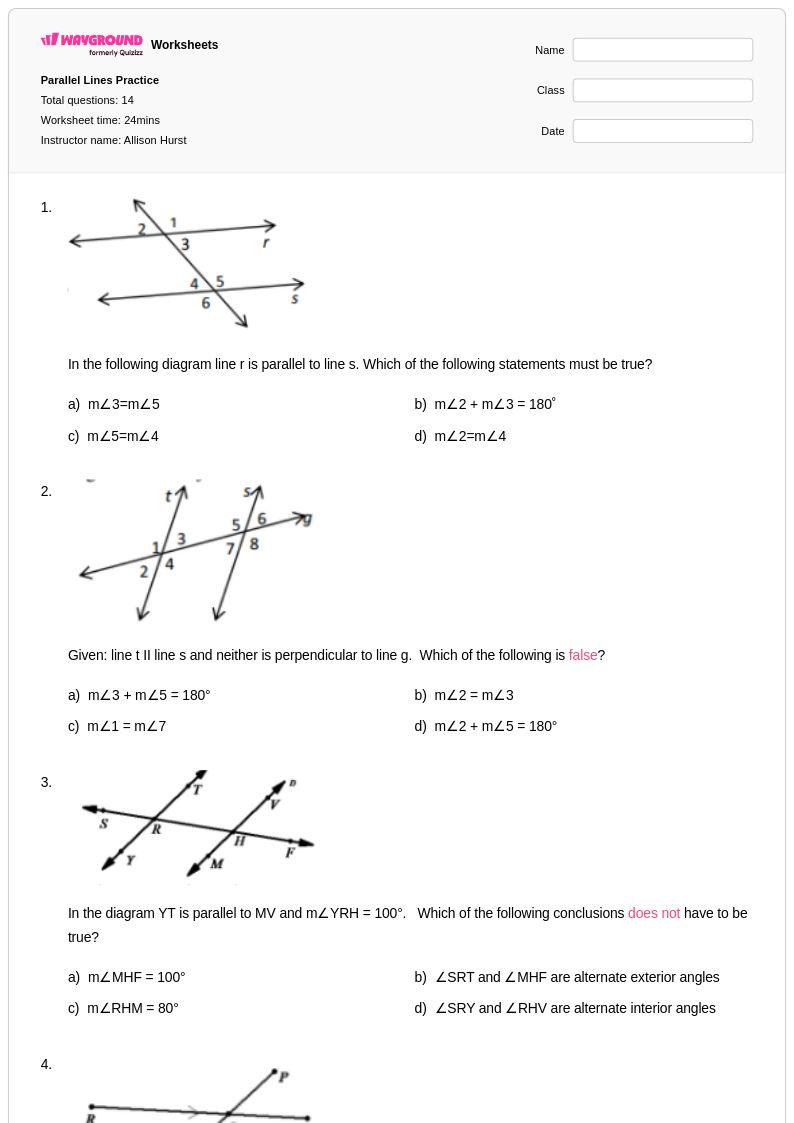
14 คิว
9th - 11th

20 คิว
11th

12 คิว
8th - 11th

20 คิว
8th - 11th

10 คิว
9th - 11th
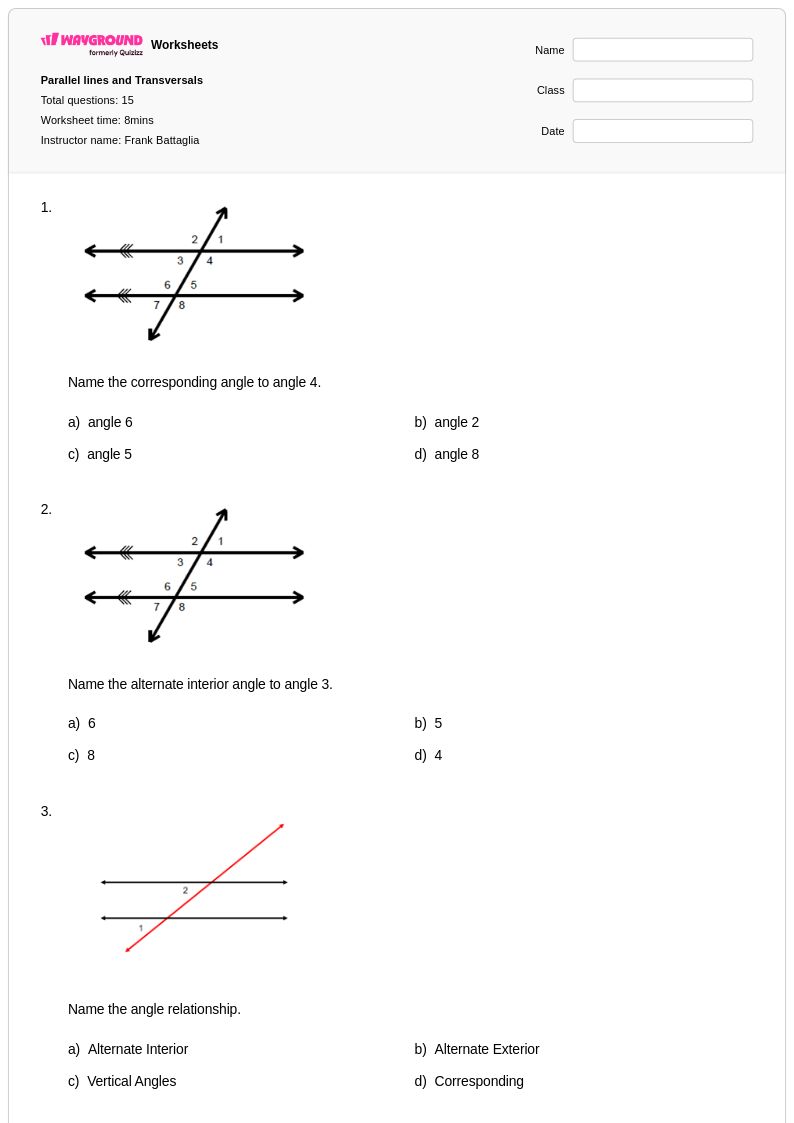
15 คิว
8th - 11th
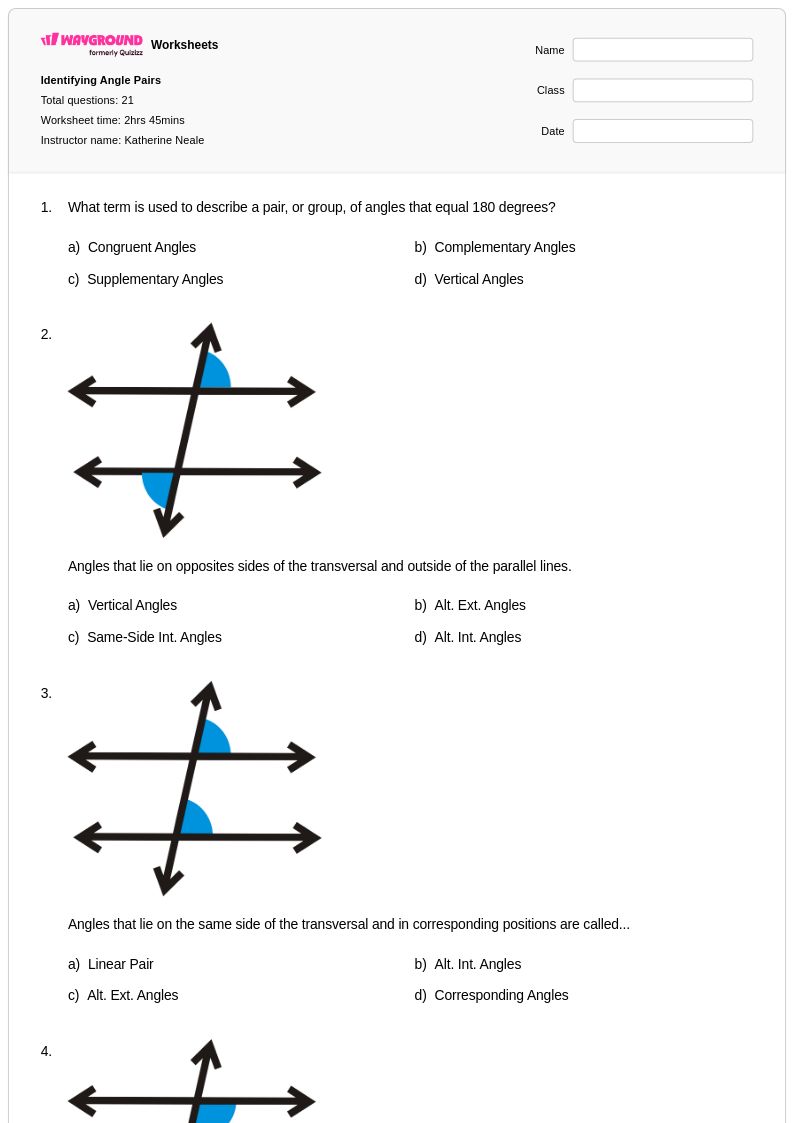
21 คิว
9th - 11th
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 11
สำรวจแผ่นงาน เส้นตัดขวางของเส้นขนาน ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 11
แบบฝึกหัดเรื่องเส้นตัดขวางของเส้นขนานสำหรับนักเรียนชั้นมัธยมศึกษาปีที่ 4 จาก Wayground มีแบบฝึกหัดที่ครอบคลุมเกี่ยวกับความสัมพันธ์ทางเรขาคณิตพื้นฐานที่เกิดขึ้นเมื่อเส้นตรงตัดกับเส้นขนานสองเส้นขึ้นไป แหล่งข้อมูลที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยให้นักเรียนเชี่ยวชาญในการระบุและคำนวณมุมที่สมนัยกัน มุมภายในและมุมภายนอกสลับกัน มุมภายในร่วม และมุมตรงข้ามที่เกิดจากเส้นตัดขวาง แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียดและวิธีแก้ปัญหาทีละขั้นตอนที่ช่วยแนะนำนักเรียนในการแก้ปัญหาความสัมพันธ์ของมุมที่ซับซ้อน ในขณะที่รูปแบบ PDF ที่พิมพ์ได้ช่วยให้แจกจ่ายในห้องเรียนได้ง่าย แบบฝึกหัดฟรีจะค่อยๆ พัฒนาจากวิธีการระบุมุมพื้นฐานไปจนถึงการคำนวณหลายขั้นตอนขั้นสูงที่เกี่ยวข้องกับนิพจน์พีชคณิต ช่วยให้นักเรียนพัฒนาทักษะการวิเคราะห์ที่จำเป็นสำหรับหลักสูตรเรขาคณิตขั้นสูง
คลังแบบฝึกหัดเรื่องเส้นตัดขวางที่สร้างโดยครูผู้สอนจำนวนมากของ Wayground มีแหล่งข้อมูลนับล้านรายการที่ออกแบบมาโดยเฉพาะเพื่อสนับสนุนการสอนเรขาคณิตชั้นมัธยมศึกษาปีที่ 4 ด้วยความสามารถในการค้นหาและกรองที่มีประสิทธิภาพ ช่วยให้ผู้สอนสามารถค้นหาสื่อที่สอดคล้องกับมาตรฐานการเรียนรู้เฉพาะได้อย่างรวดเร็ว เครื่องมือปรับระดับความยากง่ายของแพลตฟอร์มช่วยให้ครูสามารถปรับแต่งแบบฝึกหัดให้เหมาะสมกับระดับทักษะที่แตกต่างกัน ในขณะที่ตัวเลือกการจัดรูปแบบที่ยืดหยุ่นช่วยให้สามารถสร้างทั้งแบบฝึกหัดดิจิทัลและไฟล์ PDF ที่พิมพ์ได้ เพื่อรองรับความต้องการที่หลากหลายในห้องเรียน ชุดสื่อการสอนที่ครอบคลุมเหล่านี้สนับสนุนการวางแผนบทเรียนที่มีประสิทธิภาพ โดยนำเสนอสื่อสำหรับการแนะนำทักษะเบื้องต้น การแก้ไขปัญหาเฉพาะจุดสำหรับนักเรียนที่เรียนรู้ช้า และโอกาสในการเสริมสร้างความรู้สำหรับผู้เรียนที่มีความสามารถสูง เพื่อให้มั่นใจว่านักเรียนทุกคนสามารถพัฒนาความเชี่ยวชาญเกี่ยวกับความสัมพันธ์ของมุมตัดขวางได้ผ่านการฝึกฝนและการประเมินผลอย่างมุ่งเน้น
