
20 คิว
9th - 12th

20 คิว
10th - Uni

20 คิว
10th - Uni

18 คิว
9th - 12th
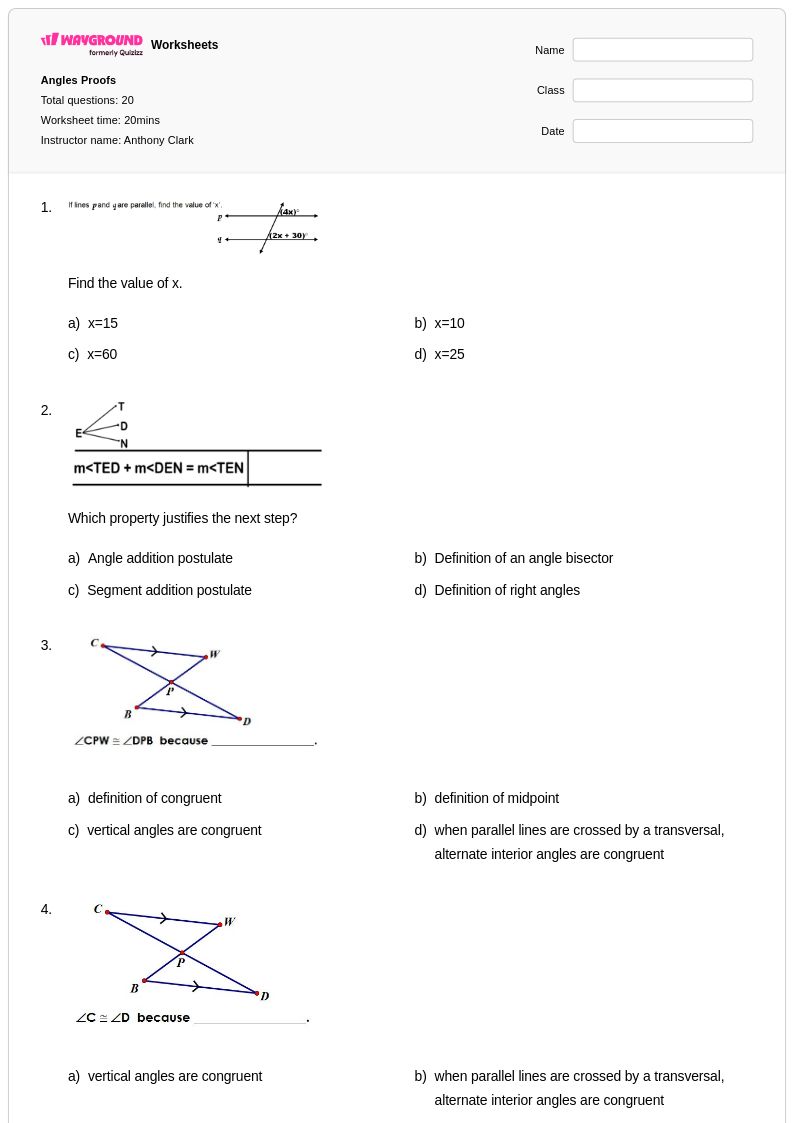
20 คิว
10th - Uni

15 คิว
10th - Uni
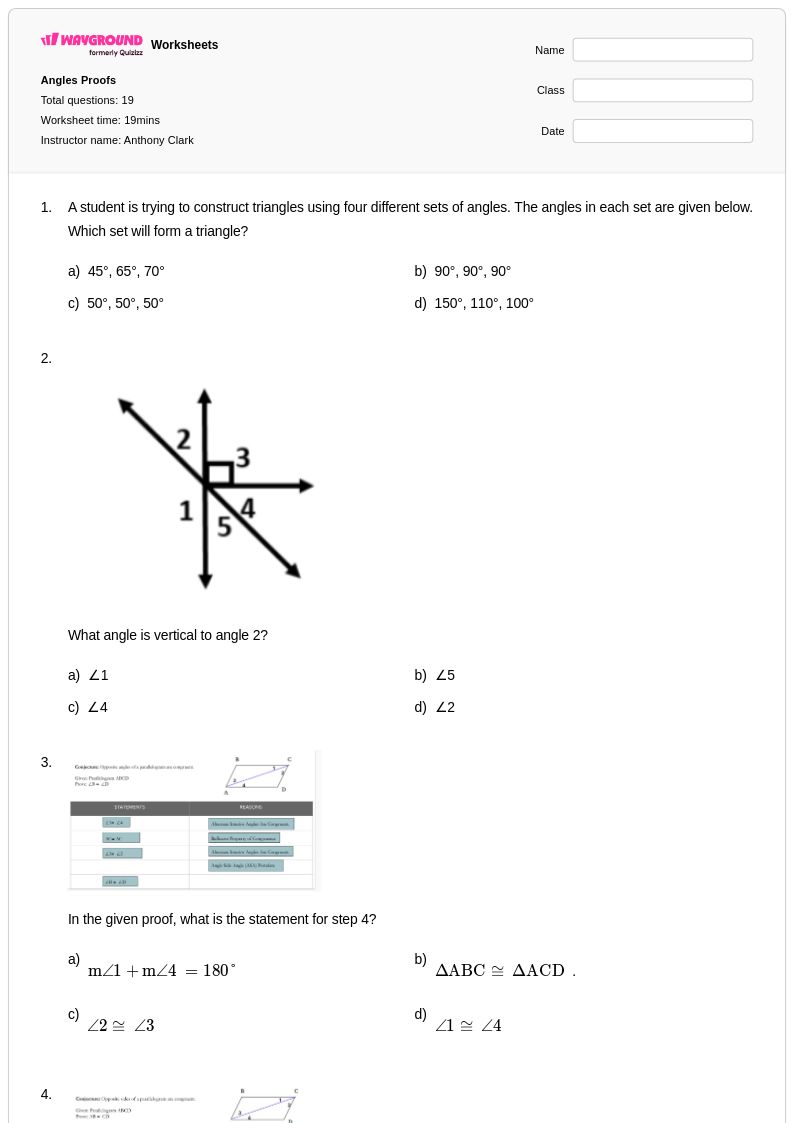
19 คิว
10th - Uni
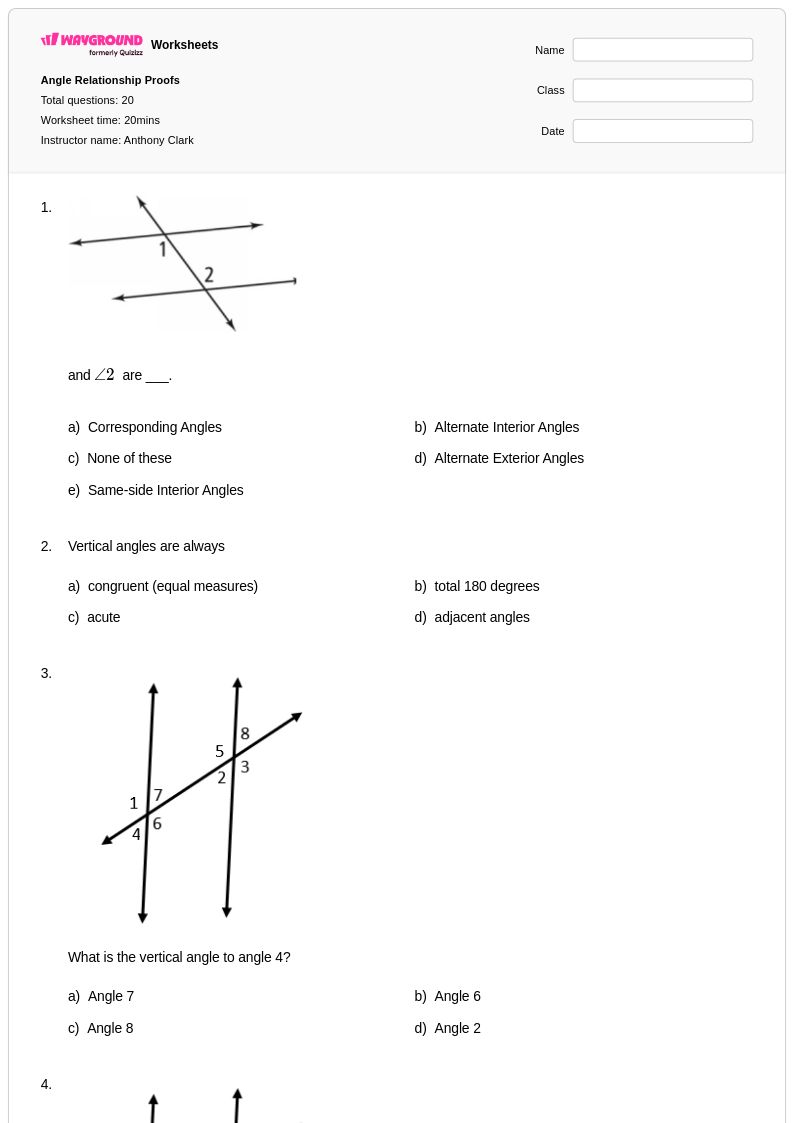
20 คิว
10th - Uni

20 คิว
9th - 12th

13 คิว
9th - 12th

20 คิว
9th - 12th
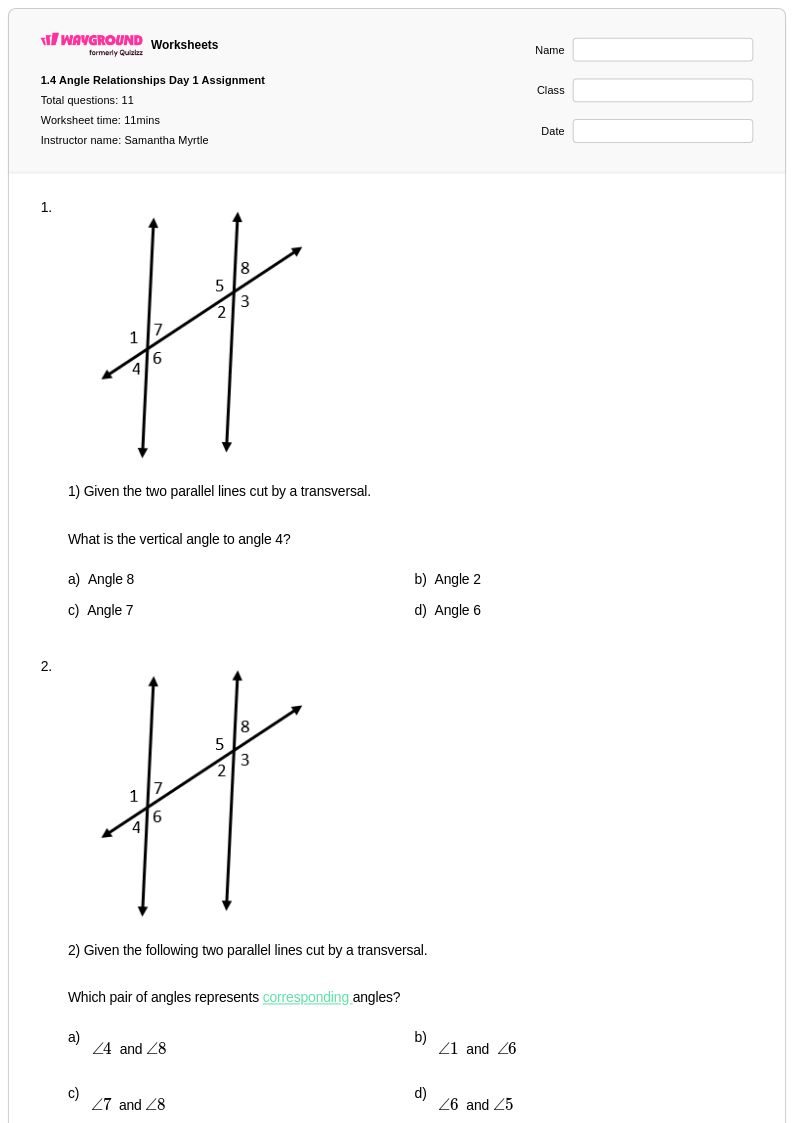
11 คิว
9th - 12th
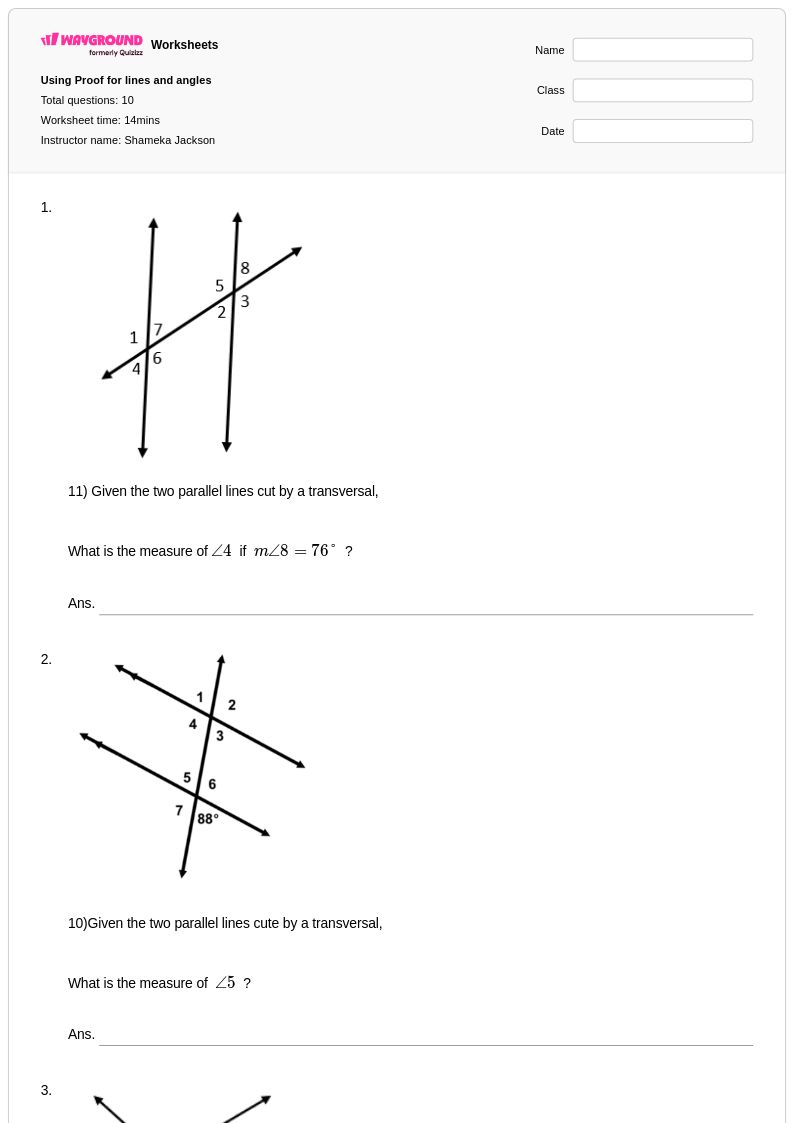
10 คิว
10th - 11th

16 คิว
9th - 12th

40 คิว
9th - 12th
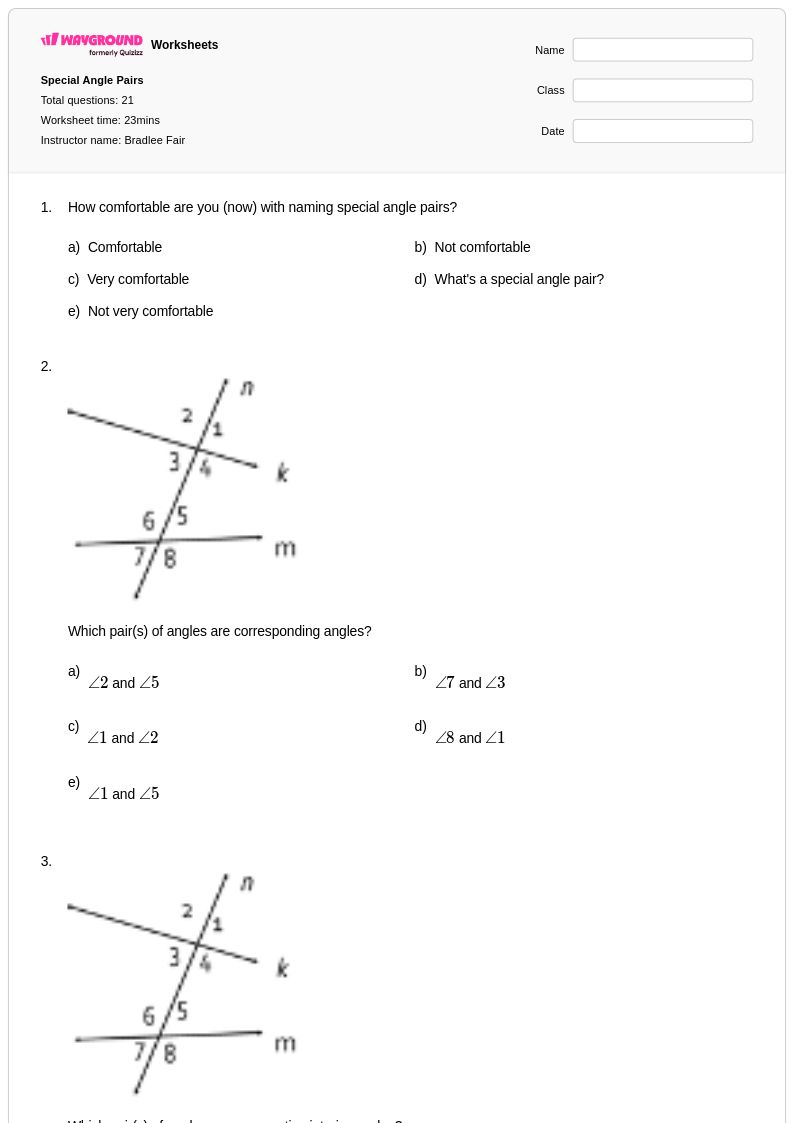
21 คิว
9th - 12th

20 คิว
9th - 12th
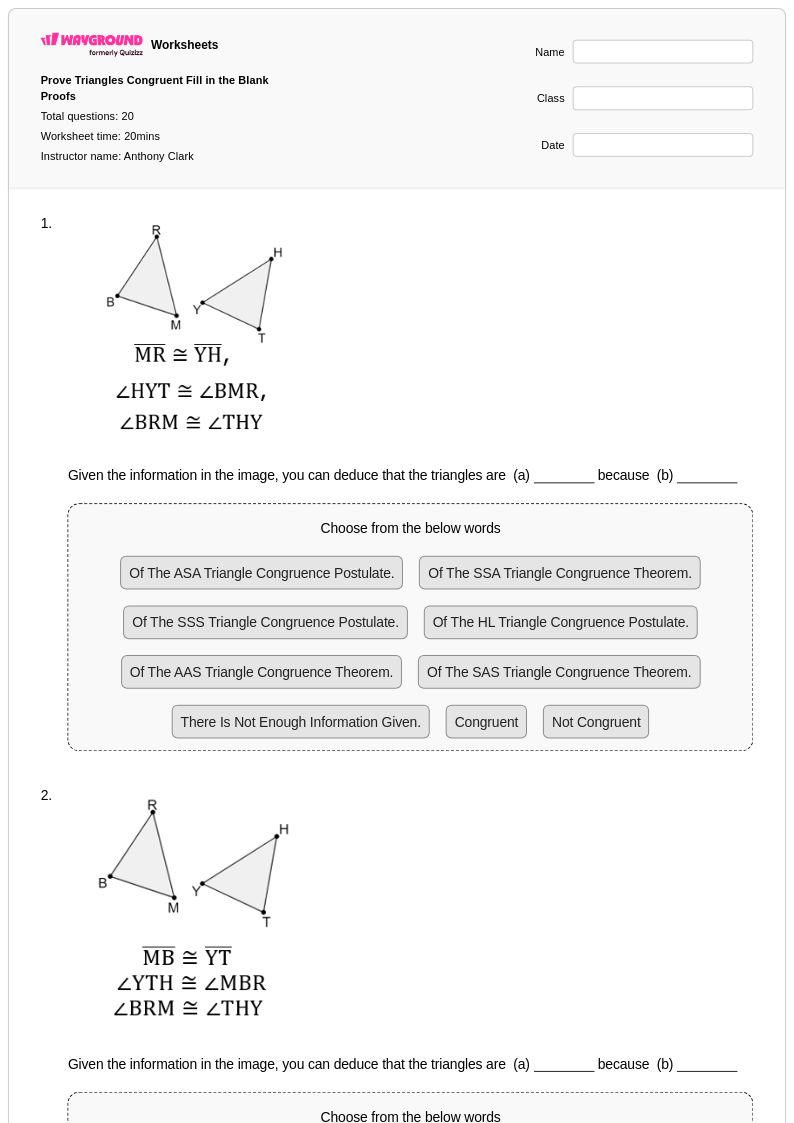
20 คิว
10th - Uni
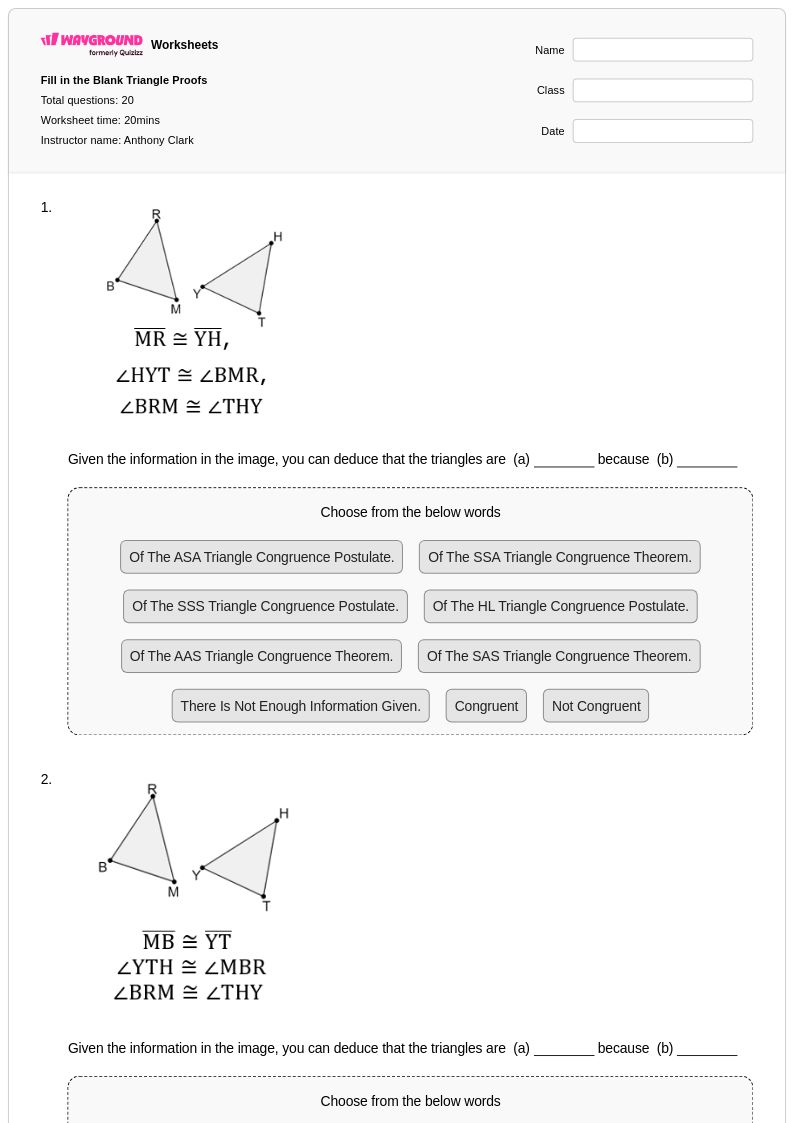
20 คิว
10th - Uni
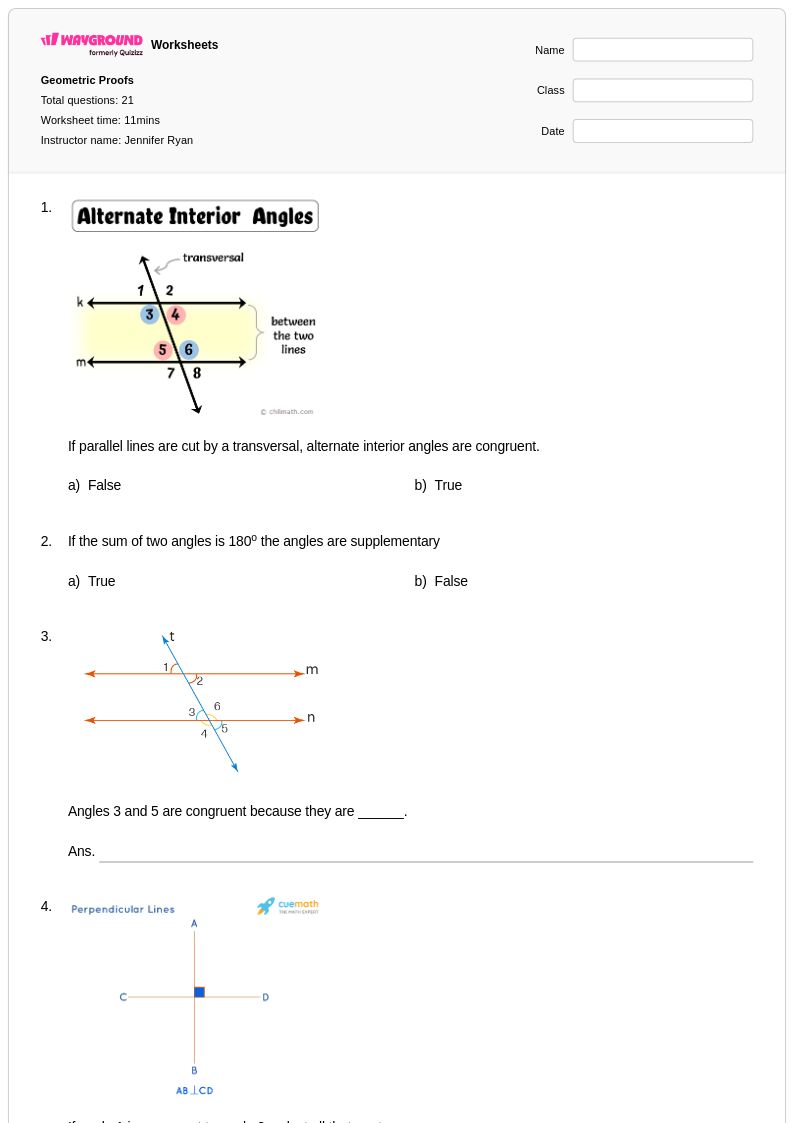
21 คิว
9th - 12th
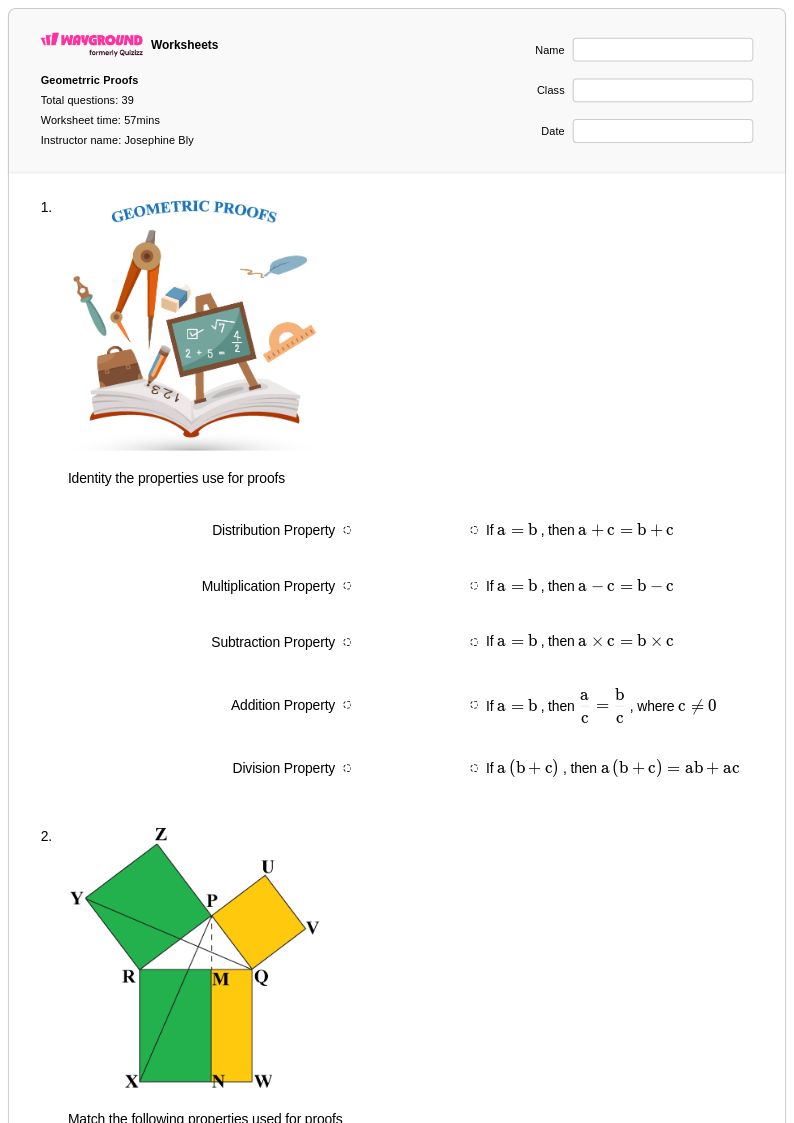
39 คิว
9th - 12th

10 คิว
10th - 11th

20 คิว
10th - Uni
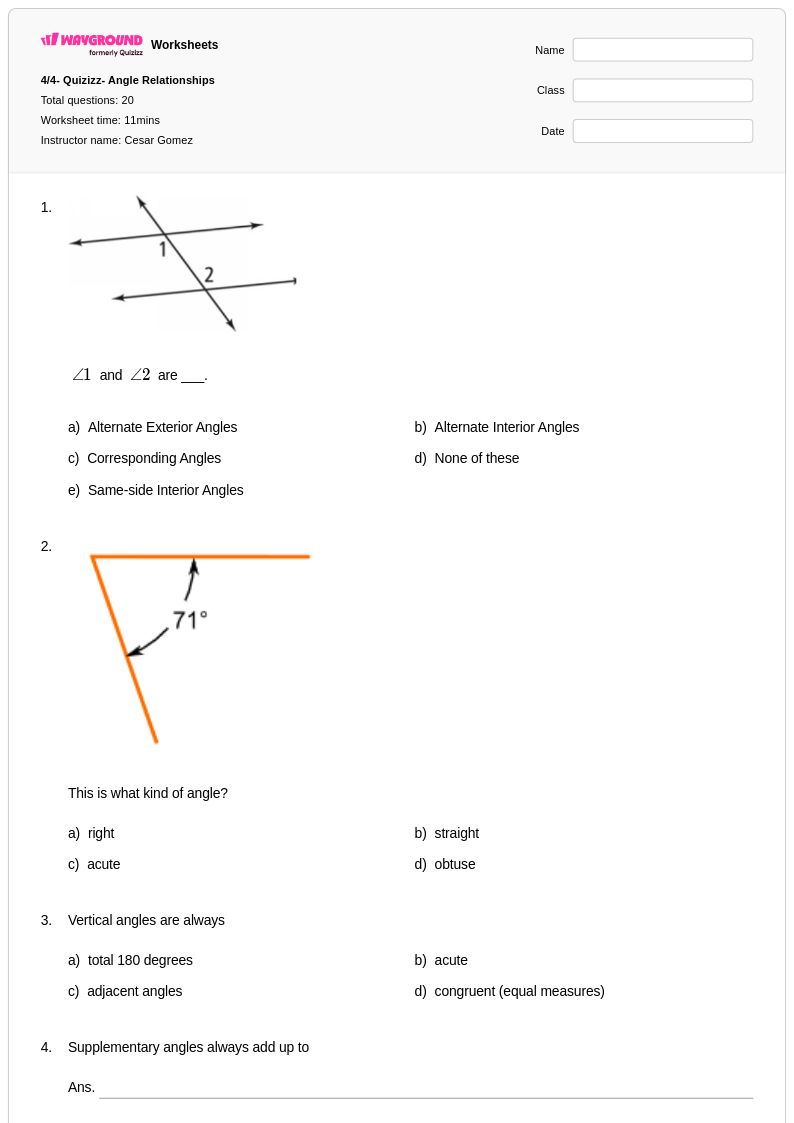
20 คิว
9th - 12th
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 11
สำรวจแผ่นงาน การพิสูจน์มุม ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 11
การพิสูจน์มุมเป็นหนึ่งในหัวข้อพื้นฐานและท้าทายที่สุดของเรขาคณิตระดับชั้นมัธยมศึกษาปีที่ 4 ซึ่งต้องอาศัยทักษะการใช้เหตุผลเชิงตรรกะอย่างเข้มงวดในการประยุกต์ใช้ทฤษฎีบทและสัจพจน์ทางเรขาคณิต ชุดแบบฝึกหัดการพิสูจน์มุมที่ครอบคลุมของ Wayground ช่วยให้นักเรียนได้ฝึกฝนอย่างเป็นระบบในการสร้างข้อโต้แย้งทางคณิตศาสตร์อย่างเป็นทางการ โดยใช้คุณสมบัติของเส้นขนาน สามเหลี่ยม และรูปหลายเหลี่ยมเพื่อสร้างความสัมพันธ์ระหว่างมุม แบบฝึกหัดที่ออกแบบมาอย่างพิถีพิถันเหล่านี้จะนำทางนักเรียนผ่านกระบวนการที่สำคัญ ได้แก่ การระบุข้อมูลที่กำหนด การระบุสิ่งที่ต้องพิสูจน์ และการพัฒนาลำดับตรรกะทีละขั้นตอนที่เชื่อมโยงข้อสมมติฐานกับข้อสรุป แบบฝึกหัดแต่ละชุดมีเฉลยคำตอบโดยละเอียดที่แสดงรูปแบบการพิสูจน์และเหตุผลทางคณิตศาสตร์ที่ถูกต้อง และรูปแบบไฟล์ PDF ที่พิมพ์ได้ฟรีช่วยให้สามารถแจกจ่ายได้อย่างสะดวกสำหรับการใช้งานในห้องเรียนและการศึกษาด้วยตนเอง
คลังข้อมูลขนาดใหญ่ของ Wayground ซึ่งสร้างขึ้นจากแหล่งข้อมูลที่สร้างโดยครูหลายล้านรายการ มอบเครื่องมือที่มีประสิทธิภาพแก่นักการศึกษาเพื่อสนับสนุนการสอนการพิสูจน์มุมในสภาพแวดล้อมการเรียนรู้ที่หลากหลาย แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่ทรงประสิทธิภาพ ช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานหลักสูตรเฉพาะ และมุ่งเน้นเทคนิคการพิสูจน์ต่างๆ ตั้งแต่ความสัมพันธ์ของมุมพื้นฐานไปจนถึงการให้เหตุผลทางเรขาคณิตที่ซับซ้อนหลายขั้นตอน เครื่องมือการปรับระดับความยากง่ายช่วยให้ผู้สอนสามารถปรับระดับความยากของแบบฝึกหัดได้ เพื่อรองรับนักเรียนที่ต้องการความช่วยเหลือเพิ่มเติมควบคู่ไปกับนักเรียนที่พร้อมสำหรับความท้าทายขั้นสูง แหล่งข้อมูลเหล่านี้มีให้เลือกทั้งในรูปแบบดิจิทัลและไฟล์ PDF ที่สามารถพิมพ์ได้ จึงสามารถบูรณาการเข้ากับการวางแผนบทเรียนได้อย่างราบรื่น พร้อมทั้งมีตัวเลือกที่ยืดหยุ่นสำหรับช่วงการแก้ไขปัญหา การเสริมสร้างทักษะ และการฝึกฝนทักษะเฉพาะด้าน ซึ่งจะช่วยสร้างความมั่นใจให้กับนักเรียนในการให้เหตุผลทางคณิตศาสตร์อย่างเป็นทางการ
