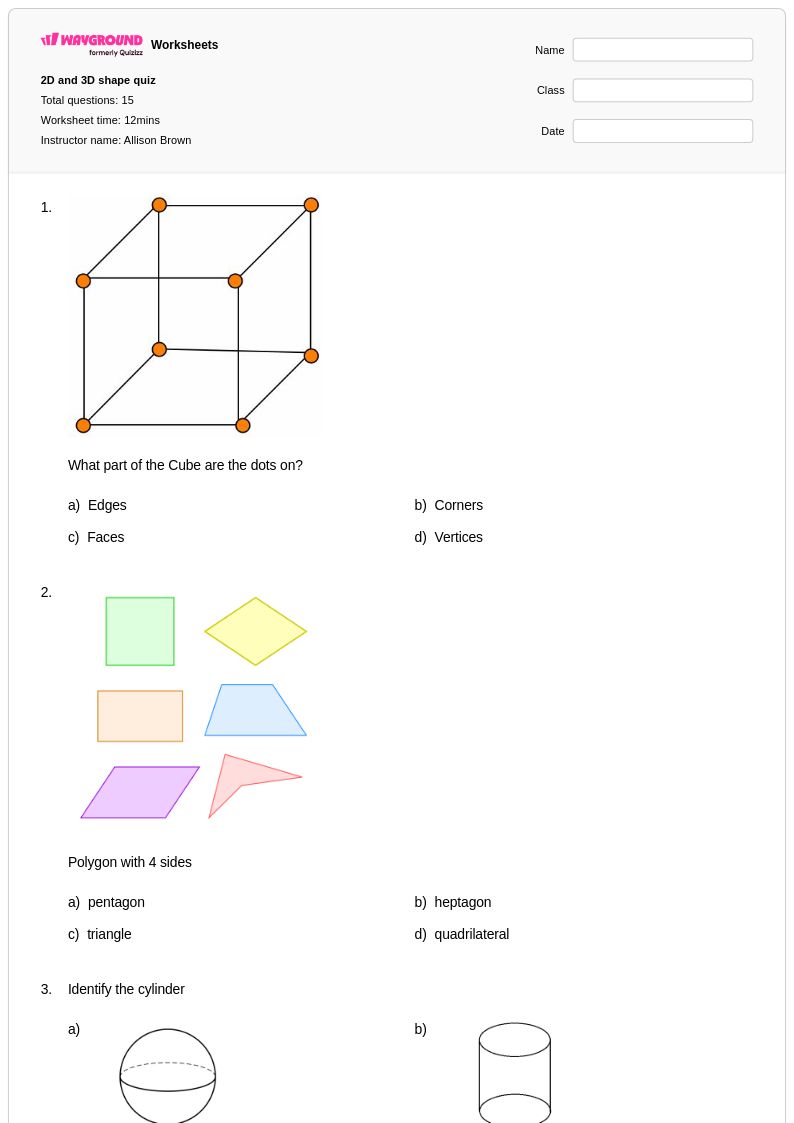
15 Hỏi
3rd
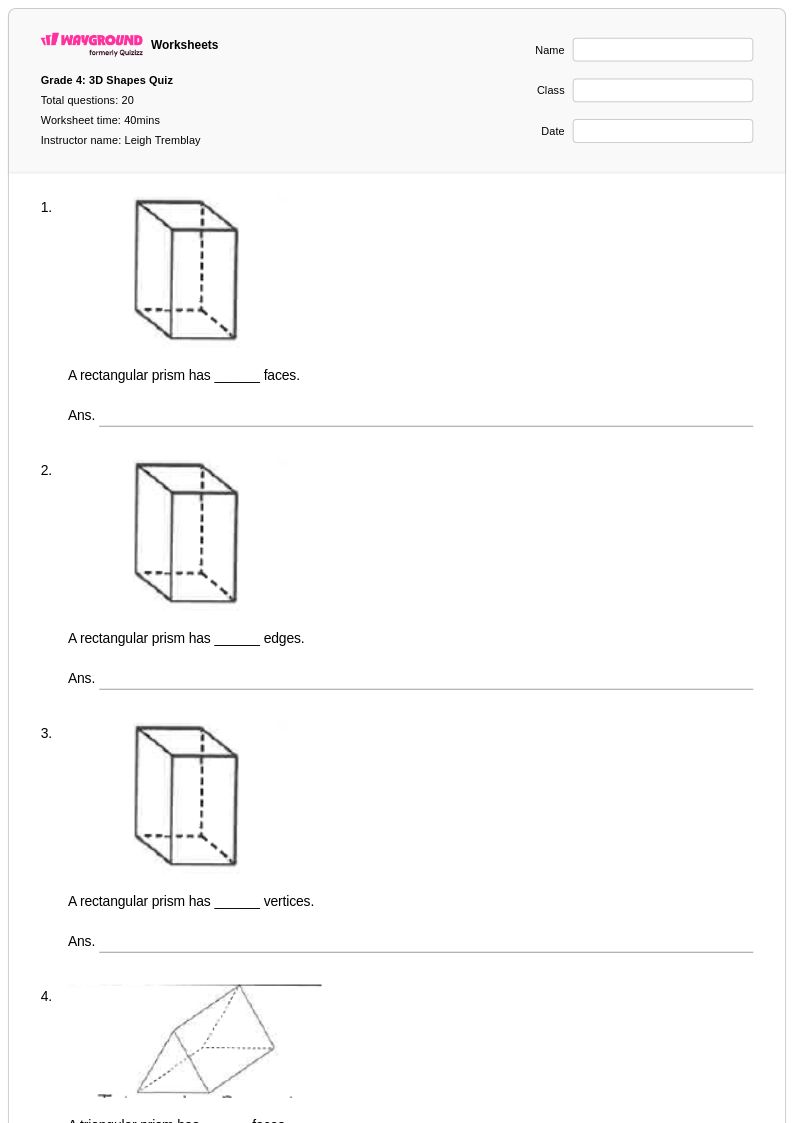
20 Hỏi
3rd - 5th
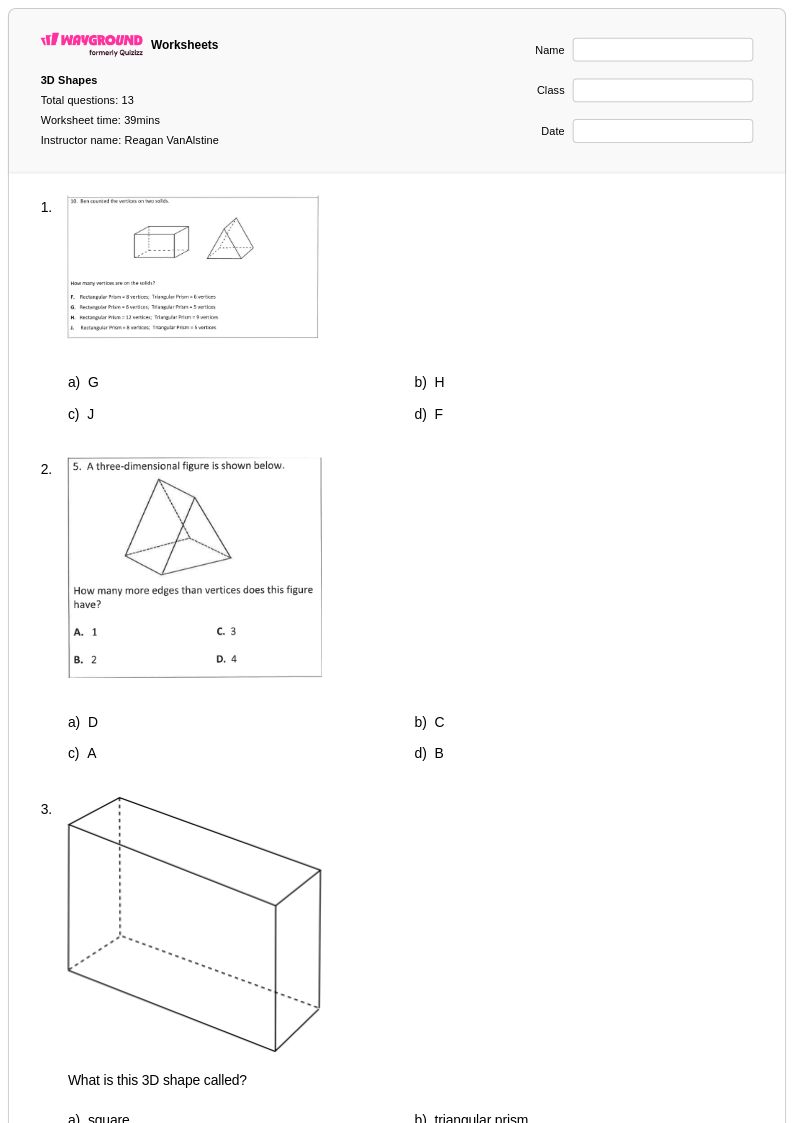
13 Hỏi
3rd

12 Hỏi
3rd

20 Hỏi
3rd
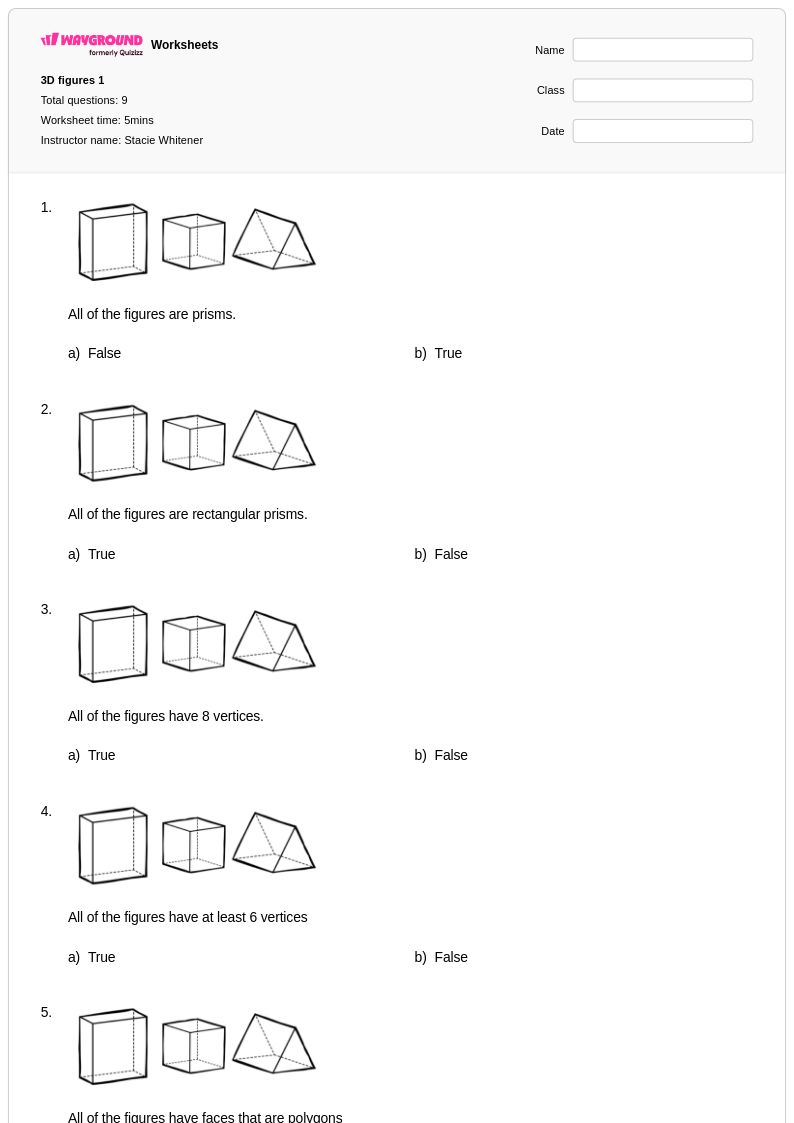
9 Hỏi
2nd - 3rd

20 Hỏi
2nd - Uni

20 Hỏi
3rd - Uni
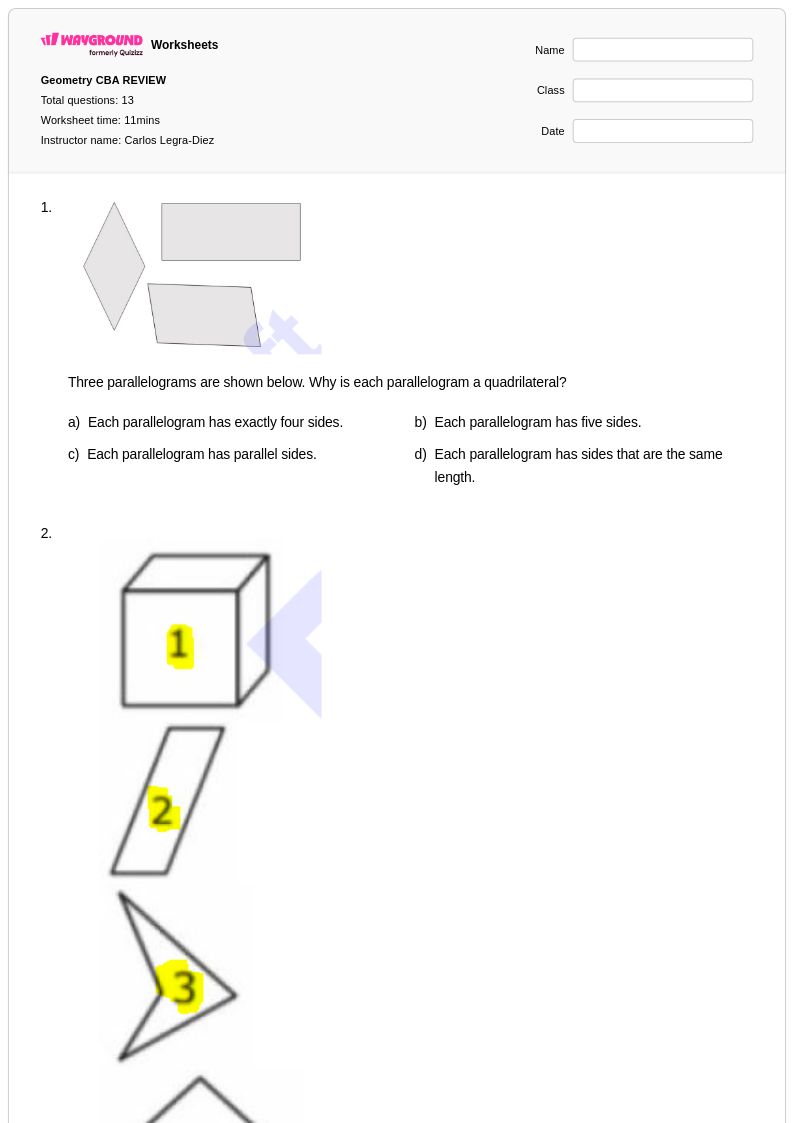
13 Hỏi
3rd

30 Hỏi
3rd

20 Hỏi
3rd - Uni
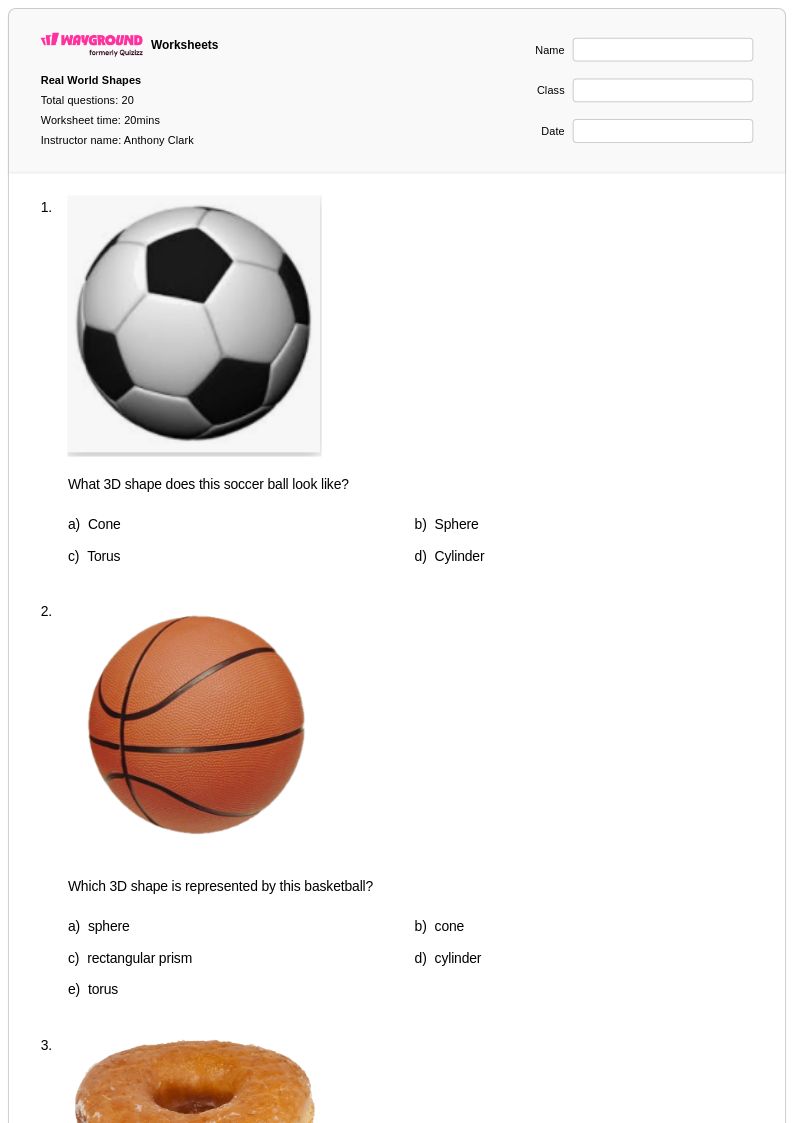
20 Hỏi
3rd - Uni

10 Hỏi
3rd

6 Hỏi
3rd - Uni
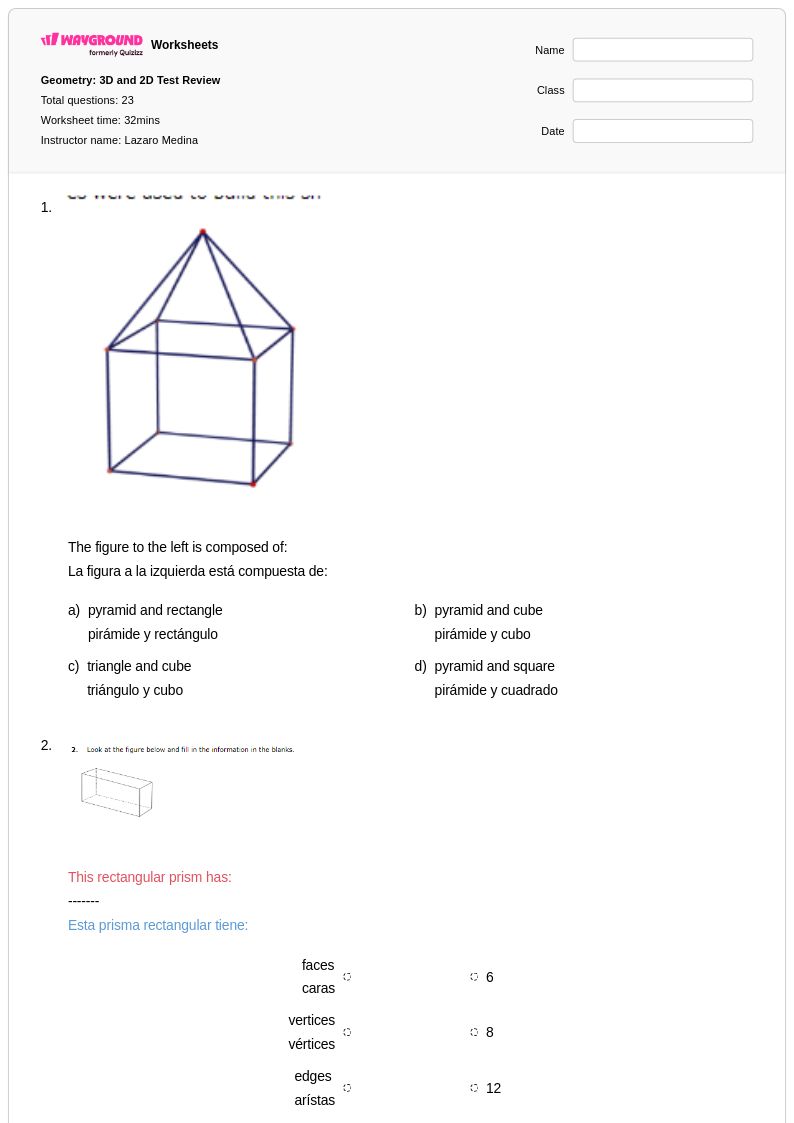
23 Hỏi
3rd

50 Hỏi
3rd

20 Hỏi
3rd - Uni

17 Hỏi
3rd

20 Hỏi
2nd - 3rd

10 Hỏi
3rd

13 Hỏi
3rd
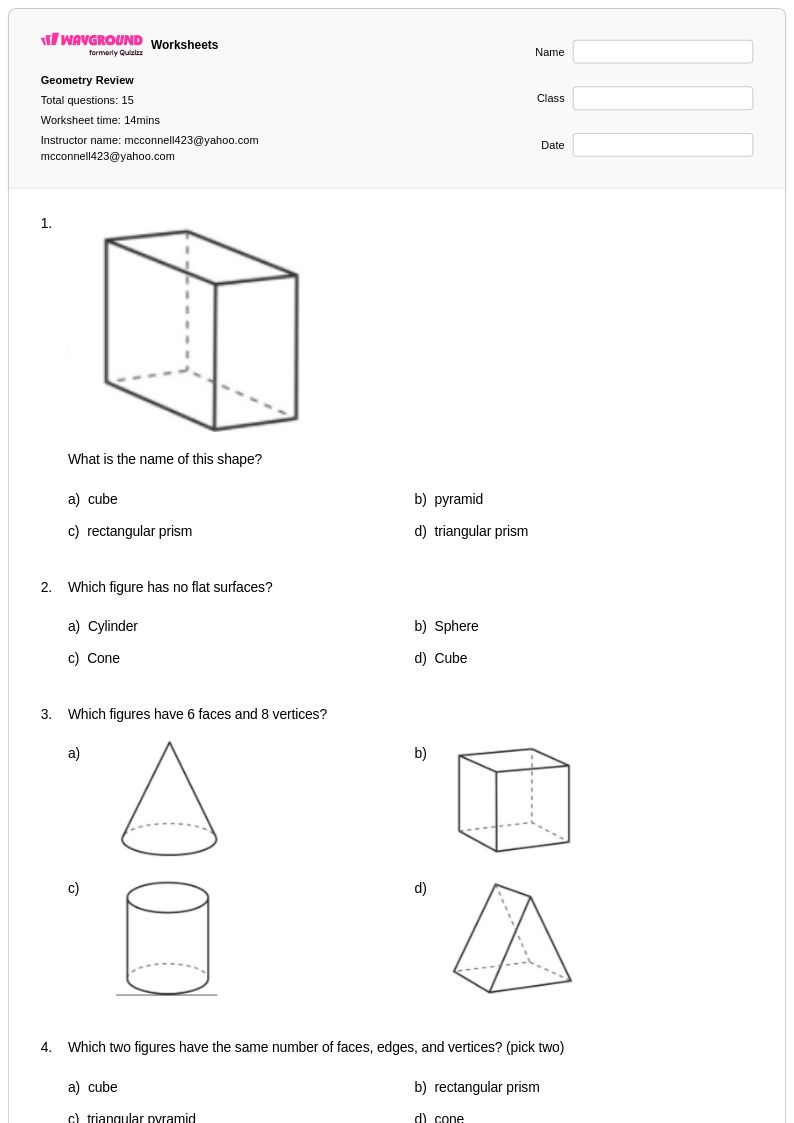
15 Hỏi
3rd

19 Hỏi
3rd - Uni
20 Hỏi
3rd
Khám phá ปริซึมสี่เหลี่ยมผืนผ้า Bảng tính theo cấp độ
Khám phá các bảng tính chủ đề khác cho ระดับ 3
สำรวจแผ่นงาน ปริซึมสี่เหลี่ยมผืนผ้า ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 3
ปริซึมสี่เหลี่ยมผืนผ้าเป็นแนวคิดพื้นฐานในเรขาคณิตระดับชั้นประถมศึกษาปีที่ 3 ที่เชื่อมโยงความเข้าใจในสองมิติกับการให้เหตุผลเชิงพื้นที่สามมิติ ชุดแบบฝึกหัดปริซึมสี่เหลี่ยมผืนผ้าที่ครอบคลุมของ Wayground ช่วยให้นักเรียนได้ฝึกฝนทักษะที่สำคัญในการระบุหน้า ขอบ และจุดยอด พร้อมทั้งสร้างความเข้าใจพื้นฐานเกี่ยวกับปริมาตรและพื้นที่ผิว แหล่งข้อมูลที่พิมพ์ได้ฟรีเหล่านี้มีกิจกรรมที่จัดโครงสร้างอย่างรอบคอบซึ่งแนะนำผู้เรียนระดับชั้นประถมศึกษาปีที่ 3 ผ่านการสำรวจปริซึมสี่เหลี่ยมผืนผ้าในบริบทของโลกแห่งความเป็นจริง ตั้งแต่บล็อกตัวต่อไปจนถึงกล่องซีเรียล แบบฝึกหัดแต่ละแผ่นมีเฉลยคำตอบโดยละเอียดที่สนับสนุนทั้งการเรียนรู้ด้วยตนเองและการสอนแบบมีผู้แนะนำ โดยมีรูปแบบ PDF เพื่อให้ง่ายต่อการแจกจ่ายในห้องเรียนและการฝึกฝนที่บ้าน
คลังข้อมูลขนาดใหญ่ของ Wayground รวบรวมทรัพยากรที่สร้างโดยครูหลายล้านรายการ ซึ่งออกแบบมาโดยเฉพาะเพื่อตอบสนองความต้องการที่หลากหลายของห้องเรียนในการสอนเรขาคณิตระดับประถมศึกษา ความสามารถในการค้นหาและการกรองที่มีประสิทธิภาพของแพลตฟอร์มช่วยให้ครูผู้สอนสามารถค้นหาแบบฝึกหัดปริซึมสี่เหลี่ยมผืนผ้าที่สอดคล้องกับมาตรฐานของรัฐและแตกต่างกันไปตามระดับทักษะต่างๆ ในหลักสูตรคณิตศาสตร์ระดับชั้นประถมศึกษาปีที่ 3 ได้อย่างรวดเร็ว ครูผู้สอนจะได้รับประโยชน์จากเครื่องมือปรับแต่งที่ยืดหยุ่น ซึ่งช่วยให้สามารถแก้ไขสื่อการเรียนการสอนที่มีอยู่เพื่อการแก้ไขปัญหาหรือเสริมสร้างความรู้ ในขณะที่การมีให้เลือกทั้งไฟล์ PDF ที่สามารถพิมพ์ได้และรูปแบบดิจิทัลแบบโต้ตอบ ช่วยรองรับสภาพแวดล้อมการเรียนรู้และระดับการเข้าถึงเทคโนโลยีที่แตกต่างกัน แนวทางที่ครอบคลุมนี้สนับสนุนการวางแผนบทเรียนเชิงกลยุทธ์และการฝึกฝนทักษะที่ตรงเป้าหมาย ทำให้มั่นใจได้ว่านักเรียนจะพัฒนาความเข้าใจพื้นฐานที่มั่นคงเกี่ยวกับรูปทรงสามมิติ ซึ่งเตรียมความพร้อมสำหรับแนวคิดทางเรขาคณิตขั้นสูงในระดับชั้นเรียนถัดไป
