
14 คิว
4th - 11th
10 คิว
5th

20 คิว
4th - 5th

22 คิว
3rd - 5th

15 คิว
5th - 6th

16 คิว
4th - 5th

15 คิว
4th - 5th

20 คิว
4th - Uni

20 คิว
5th - Uni

14 คิว
5th

11 คิว
5th

10 คิว
5th

10 คิว
5th

23 คิว
5th

20 คิว
5th
15 คิว
5th

19 คิว
5th
80 คิว
5th

17 คิว
5th

15 คิว
5th

11 คิว
5th

10 คิว
5th - Uni

16 คิว
5th

15 คิว
5th
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 5
สำรวจแผ่นงาน ปัจจัยสำคัญ ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 5
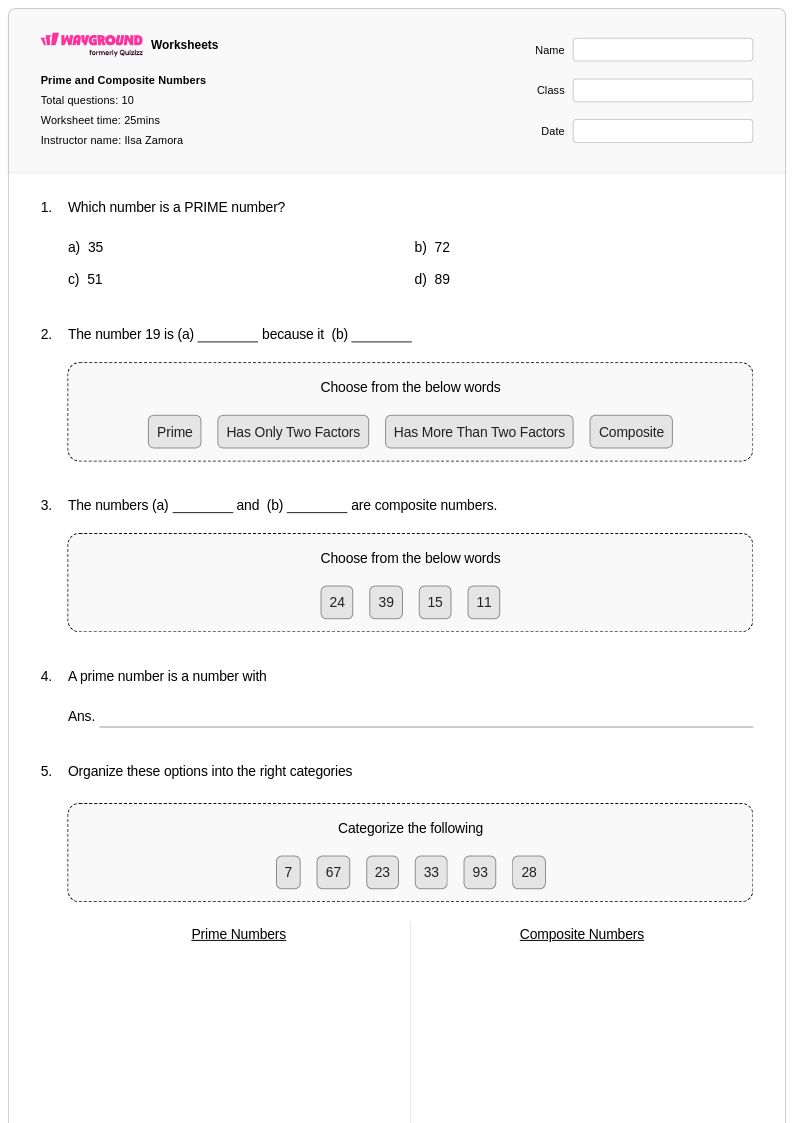
แบบฝึกหัดเรื่องตัวประกอบเฉพาะสำหรับนักเรียนชั้นประถมศึกษาปีที่ 5 จาก Wayground (เดิมชื่อ Quizizz) ให้แบบฝึกหัดที่ครอบคลุมในการแยกจำนวนประกอบออกเป็นส่วนประกอบพื้นฐาน แหล่งข้อมูลที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยเสริมสร้างความเข้าใจของนักเรียนเกี่ยวกับวิธีการที่จำนวนประกอบทุกจำนวนสามารถแสดงได้ในรูปผลคูณเฉพาะของจำนวนเฉพาะ ซึ่งเป็นแนวคิดพื้นฐานในทฤษฎีจำนวน แบบฝึกหัดมีโจทย์ฝึกฝนที่ค่อยเป็นค่อยไปซึ่งจะนำนักเรียนชั้นประถมศึกษาปีที่ 5 ผ่านวิธีการที่เป็นระบบ เช่น แผนผังตัวประกอบและบันไดการหาร ช่วยให้พวกเขามีความคล่องแคล่วในการระบุตัวประกอบเฉพาะของจำนวนในช่วงอายุที่เหมาะสม แหล่งข้อมูลที่พิมพ์ได้แต่ละชุดมีเฉลยคำตอบโดยละเอียดที่สนับสนุนการเรียนรู้ด้วยตนเองและการประเมินตนเอง ในขณะที่รูปแบบ PDF ฟรีช่วยให้เข้าถึงได้ง่ายทั้งสำหรับการสอนในห้องเรียนและการบ้าน
คอลเลกชันแบบฝึกหัดเรื่องตัวประกอบเฉพาะที่ครอบคลุมของ Wayground มาจากแหล่งข้อมูลที่สร้างโดยครูหลายล้านคน ช่วยให้ครูผู้สอนมีศักยภาพในการค้นหาและกรองข้อมูลได้อย่างมีประสิทธิภาพ เพื่อค้นหาสื่อที่เหมาะสมกับหลักสูตรคณิตศาสตร์ชั้นประถมศึกษาปีที่ 5 ของพวกเขาได้อย่างสมบูรณ์แบบ เนื้อหาของแพลตฟอร์มที่สอดคล้องกับมาตรฐานช่วยสนับสนุนการสอนที่แตกต่างกันผ่านแบบฝึกหัดที่ปรับแต่งได้ ซึ่งสามารถแก้ไขให้ตรงกับความต้องการการเรียนรู้ที่หลากหลาย ตั้งแต่แบบฝึกหัดเสริมสำหรับนักเรียนที่เรียนรู้ช้า ไปจนถึงกิจกรรมเสริมสำหรับผู้เรียนที่มีความสามารถสูง ครูผู้สอนได้รับประโยชน์จากตัวเลือกการส่งมอบที่ยืดหยุ่น โดยสามารถเข้าถึงสื่อทั้งในรูปแบบสิ่งพิมพ์และดิจิทัล ซึ่งผสานรวมเข้ากับการวางแผนบทเรียน การสอนกลุ่มเล็ก และการฝึกฝนทักษะรายบุคคลได้อย่างราบรื่น เครื่องมือที่ครอบคลุมเหล่านี้ช่วยให้ครูผู้สอนสามารถให้การสนับสนุนที่ตรงเป้าหมายในการพัฒนาทักษะการแยกตัวประกอบเฉพาะของนักเรียน ในขณะเดียวกันก็สร้างความสามารถในการให้เหตุผลเชิงตัวเลขที่จำเป็นต่อความสำเร็จในอนาคตในวิชาพีชคณิตและแนวคิดคณิตศาสตร์ขั้นสูง
