
48Q
6th - Uni

14Q
8th - 12th
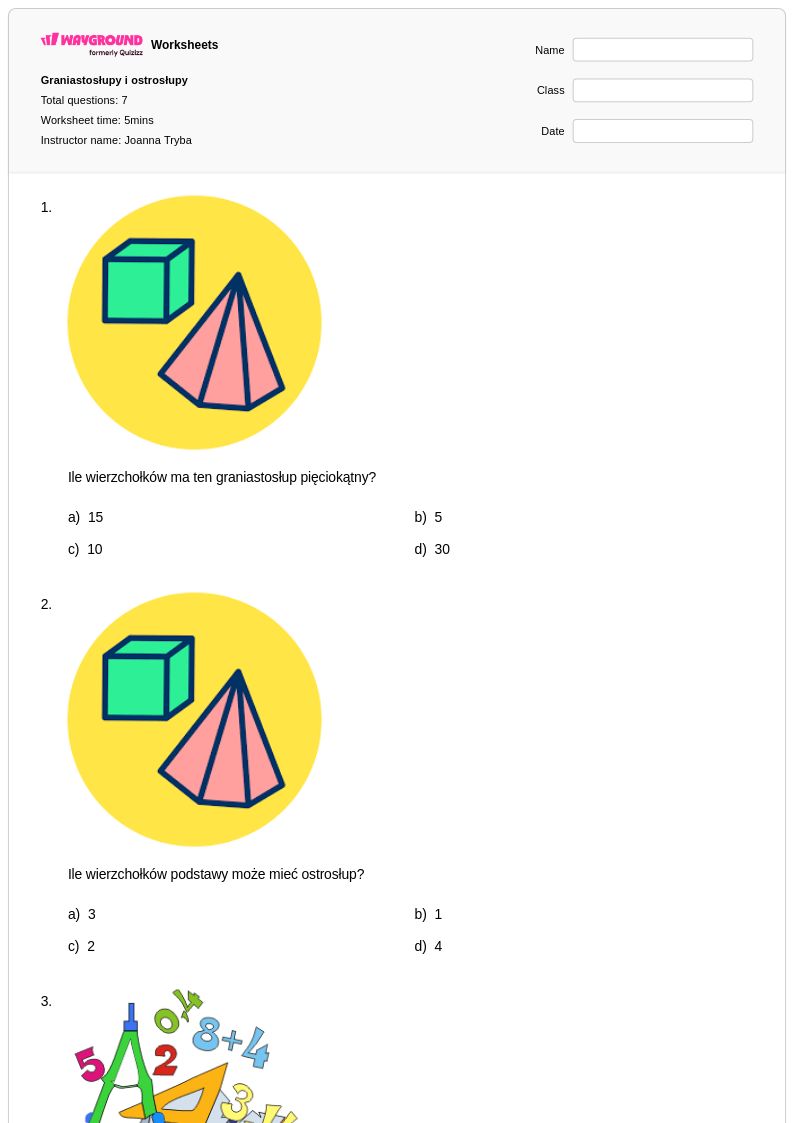
7Q
1st - 12th

10Q
8th - Uni

26Q
8th - 12th

15Q
7th - 12th
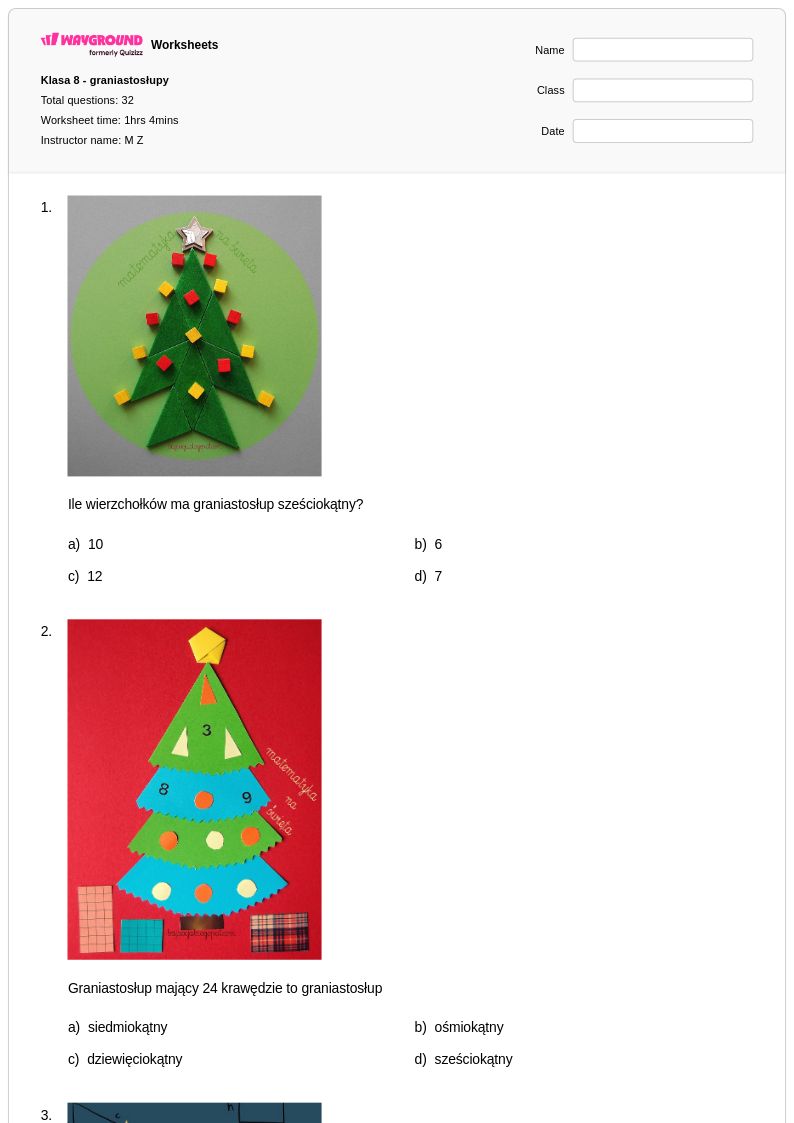
32Q
8th - Uni
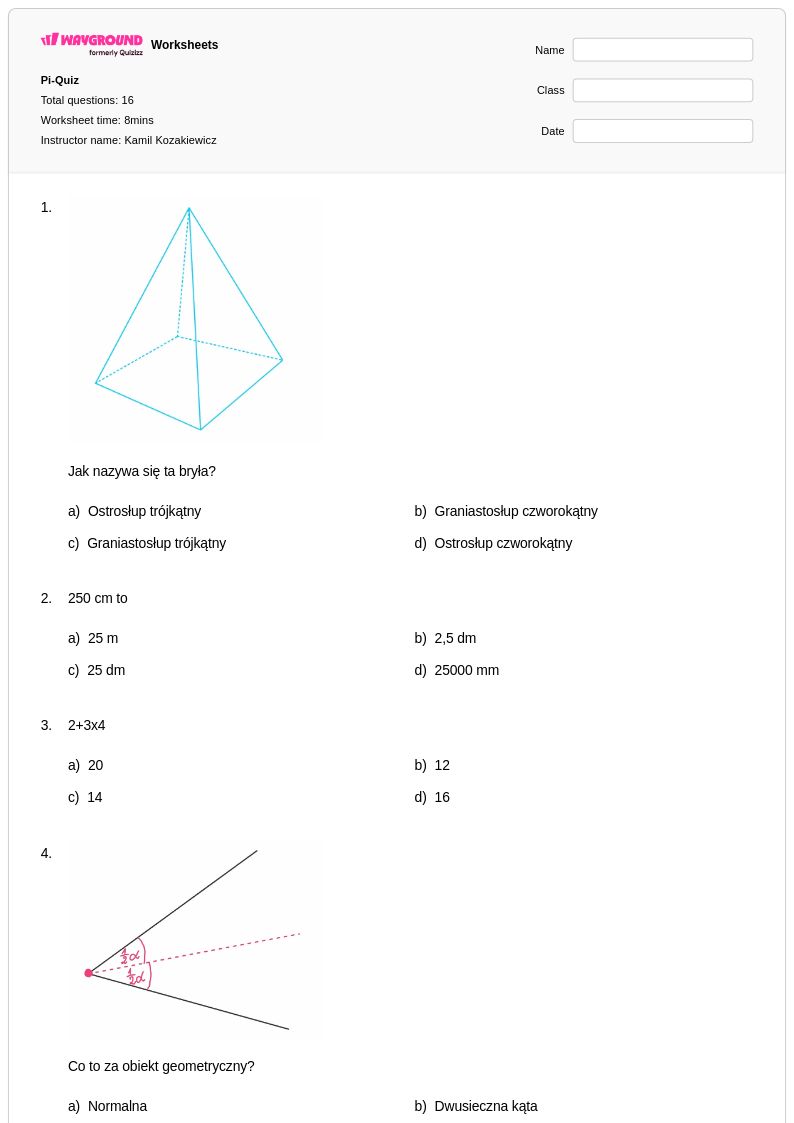
16Q
9th - 12th
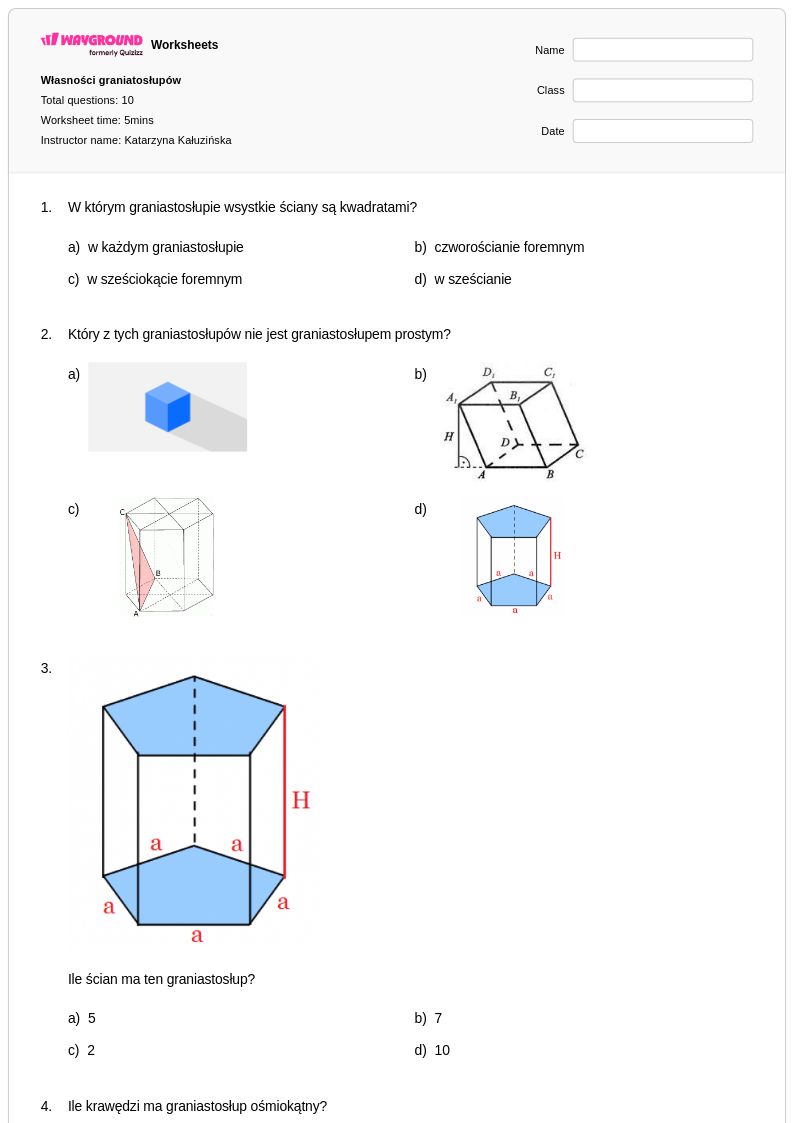
10Q
1st - 12th
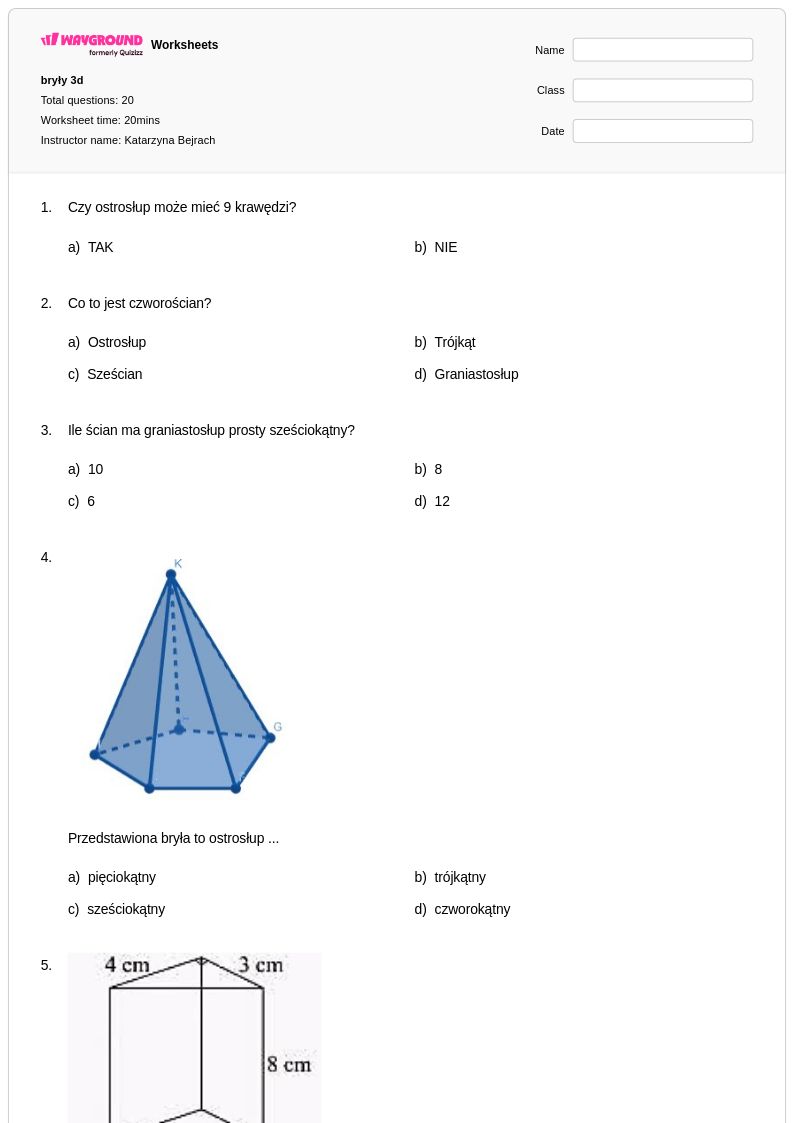
20Q
8th - 12th

61Q
11th

16Q
11th

31Q
KG - PD

45Q
5th - 12th

11Q
11th

10Q
KG - Uni

18Q
11th - Uni
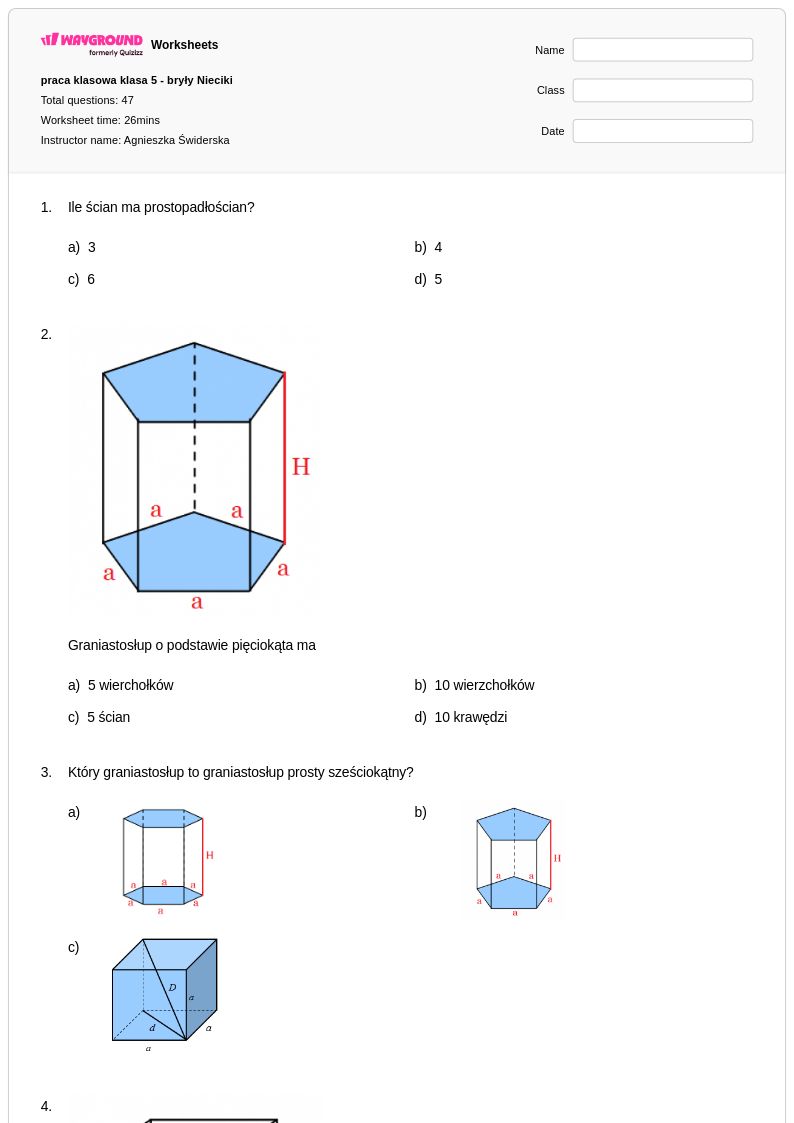
47Q
1st - 12th

20Q
1st - Uni
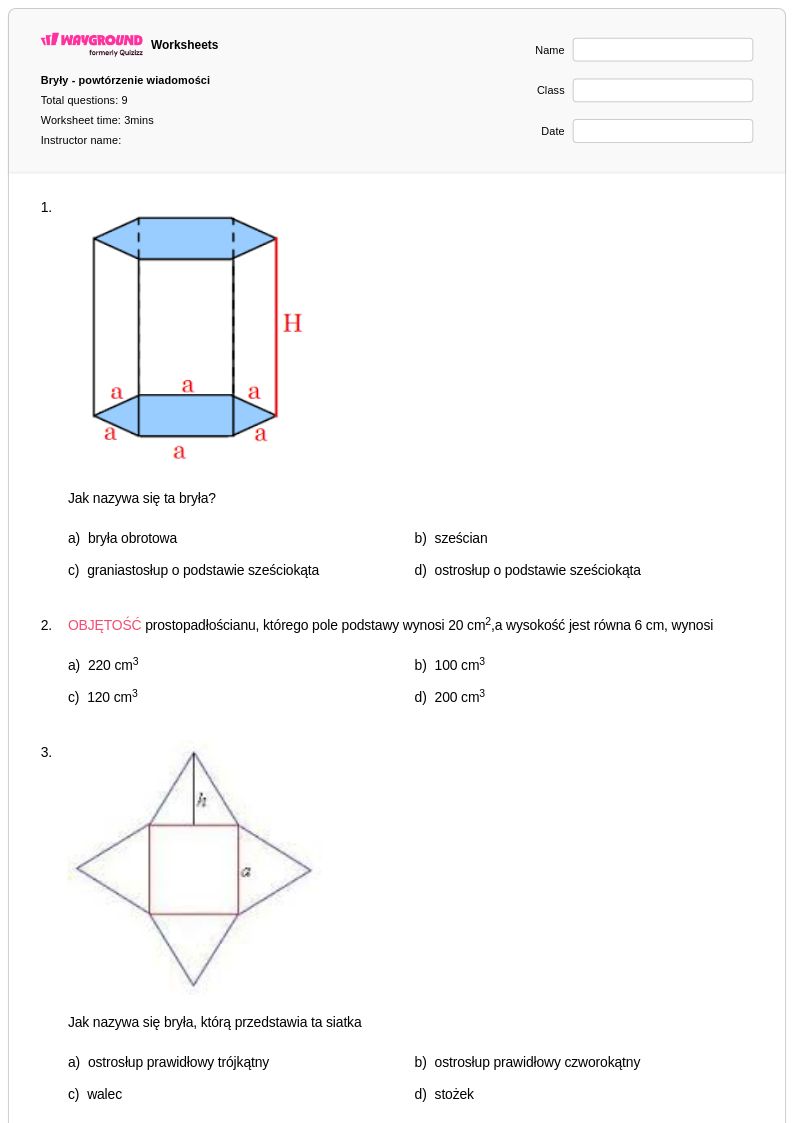
9Q
KG - Uni

6Q
1st - 12th
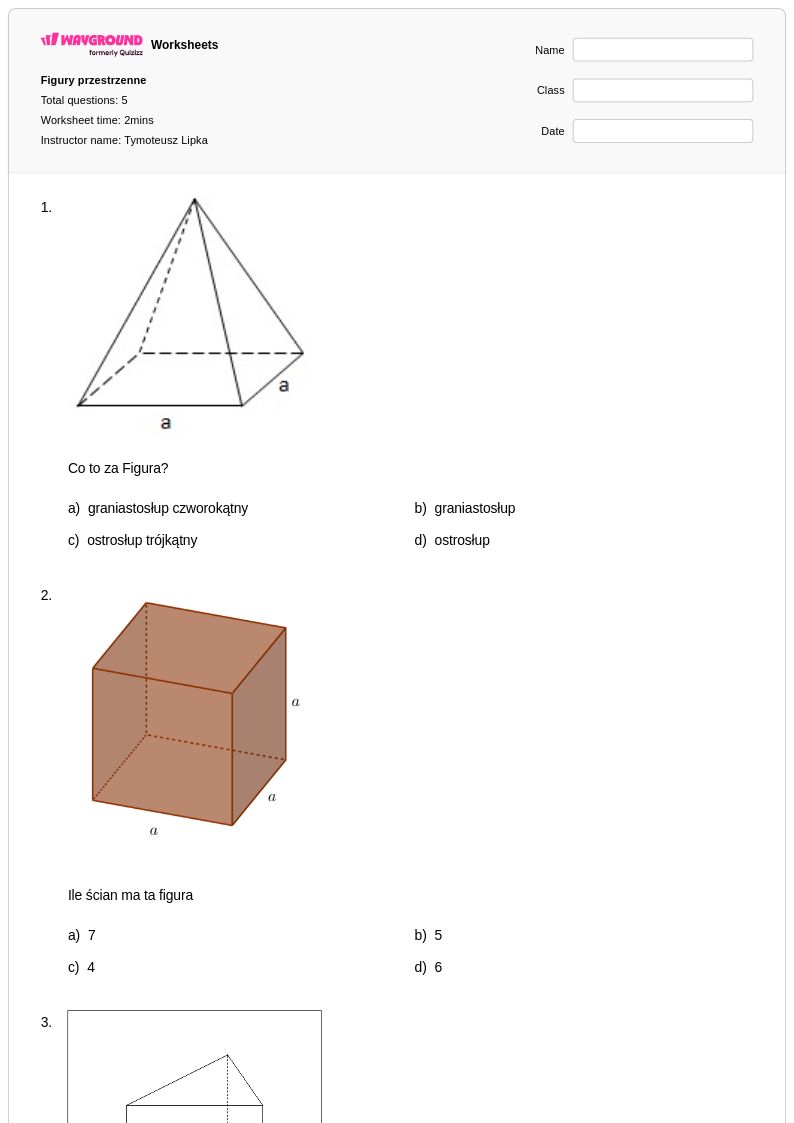
5Q
1st - 12th

29Q
11th

50Q
1st - 12th
Explore outras planilhas de assuntos para klasa 11
Przeglądaj arkusze Dowody czworokątne do wydrukowania dla Klasa 11
Dowody czworokątów stanowią kamień węgielny edukacji geometrycznej w klasie 11, wymagając od uczniów logicznego rozumowania i stosowania podstawowych zasad geometrii w celu ustalenia własności figur czworokątnych. Obszerny zbiór arkuszy dowodowych Wayground oferuje szerokie możliwości praktyczne, które wzmacniają umiejętności uczniów w zakresie konstruowania trafnych argumentów geometrycznych, wykorzystywania twierdzeń dotyczących równoległoboków, prostokątów, rombów, kwadratów i trapezów oraz rozwijania umiejętności formalnego pisania dowodów. Te starannie opracowane zadania praktyczne prowadzą uczniów przez systematyczny proces analizy podanych informacji, identyfikowania odpowiednich twierdzeń i postulatów oraz porządkowania logicznych ciągów stwierdzeń i uzasadnień. Każdy arkusz zawiera szczegółowy klucz odpowiedzi, który wspiera samodzielną naukę i samoocenę, a darmowy format PDF do wydruku zapewnia dostępność zarówno w nauczaniu w klasie, jak i w zadaniach domowych.
Solidna platforma Wayground udostępnia nauczycielom miliony zasobów dowodowych czworokątów stworzonych przez nauczycieli, które można łatwo znaleźć dzięki zaawansowanym funkcjom wyszukiwania i filtrowania, dostosowanym do standardów geometrycznych. Zaawansowane narzędzia różnicujące dostępne na platformie pozwalają nauczycielom dostosowywać arkusze ćwiczeń do indywidualnych potrzeb uczniów, zapewniając dodatkowe wsparcie uczniom mającym trudności z nauką, a także stawiając bardziej złożone zadania dowodowe uczniom na poziomie zaawansowanym. Nauczyciele mogą płynnie przechodzić między formatami cyfrowymi i drukowanymi, dzięki czemu zasoby te idealnie sprawdzają się w zróżnicowanych warunkach nauczania i preferencjach edukacyjnych. Ta elastyczność wspiera kompleksowe planowanie lekcji, zapewniając jednocześnie ukierunkowane materiały do zajęć wyrównawczych, zajęć wzbogacających i ciągłego doskonalenia umiejętności, gwarantując, że wszyscy uczniowie klasy 11. rozwiną umiejętności krytycznego myślenia i rozumowania matematycznego, niezbędne do osiągnięcia sukcesu w zaawansowanych koncepcjach geometrycznych.
