
14 คิว
12th
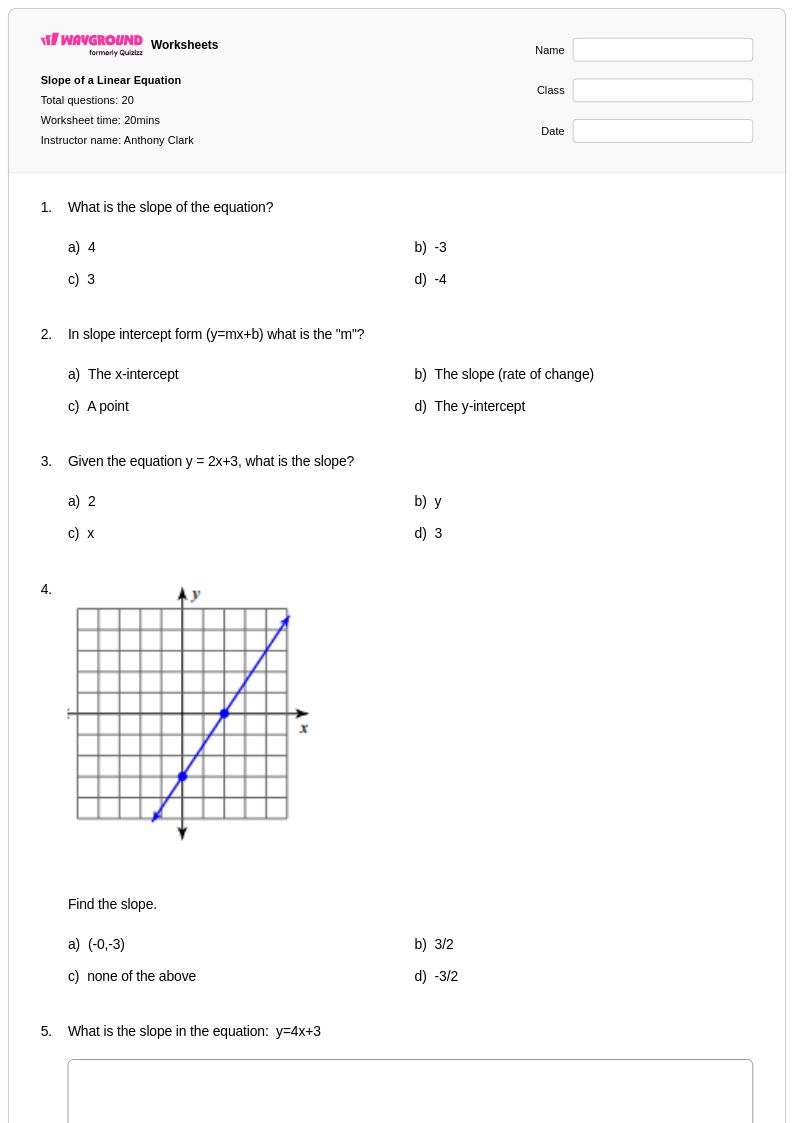
20 คิว
8th - Uni
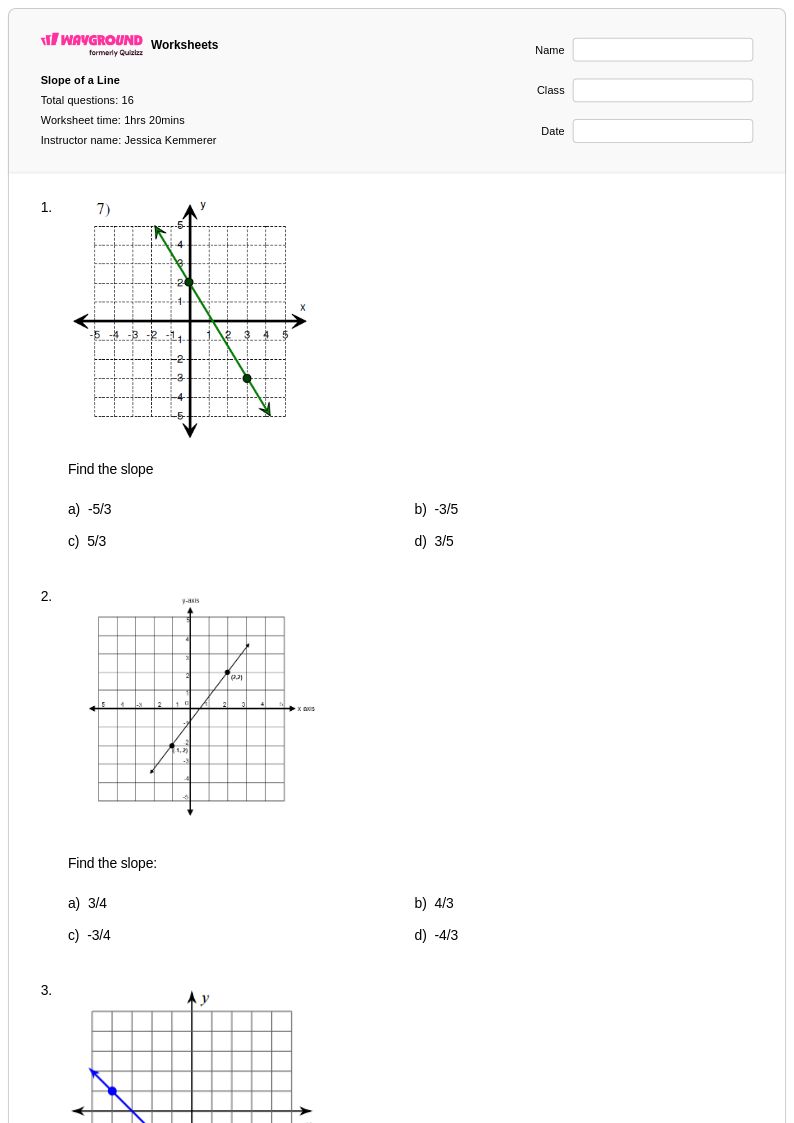
16 คิว
9th - 12th
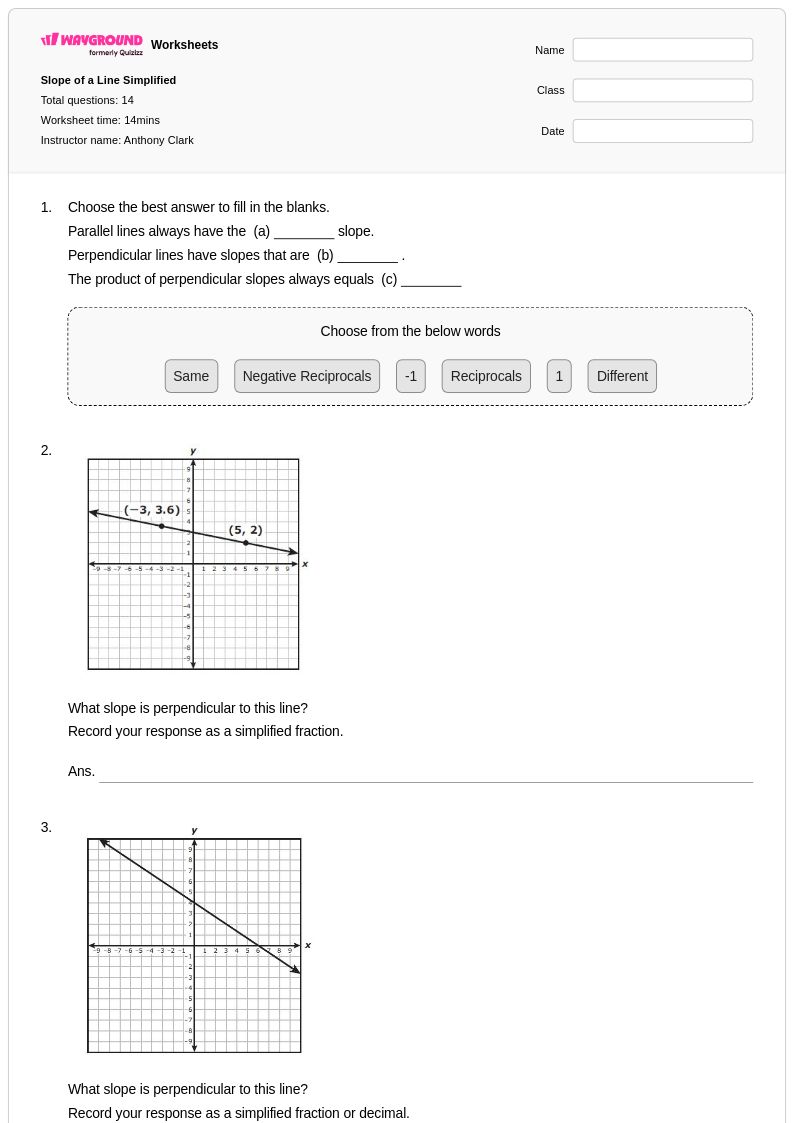
14 คิว
8th - Uni
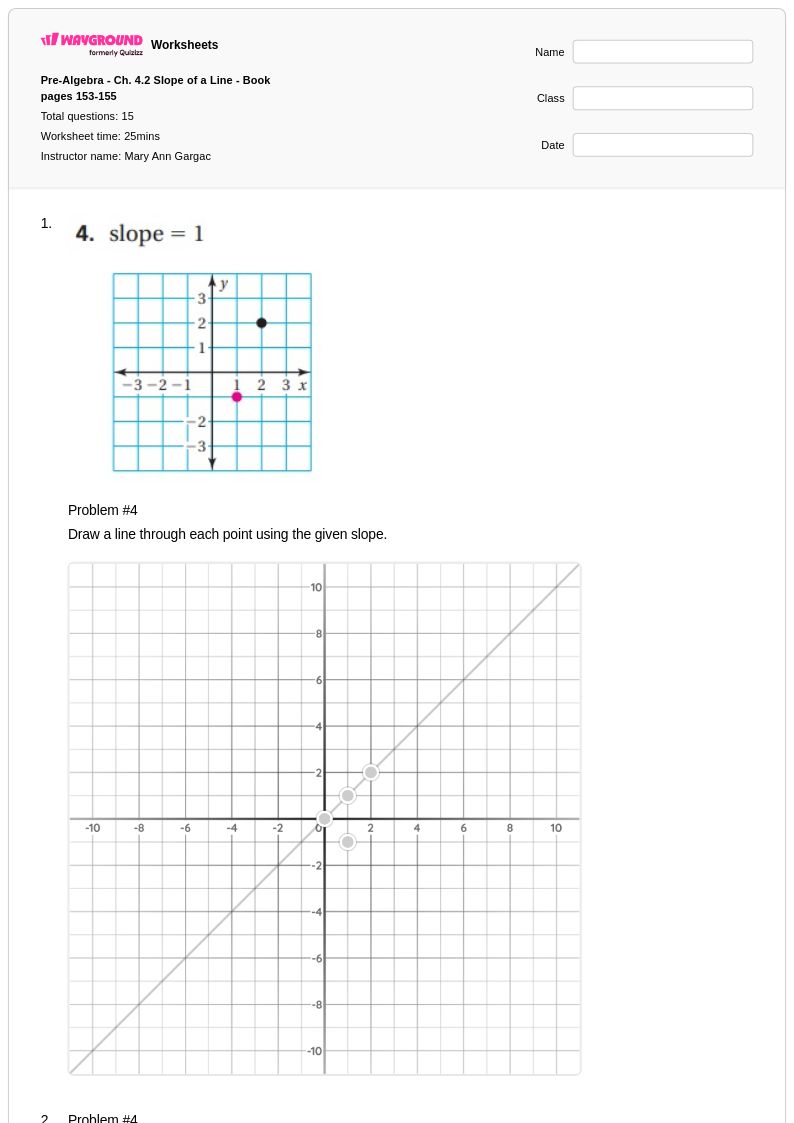
15 คิว
9th - 12th
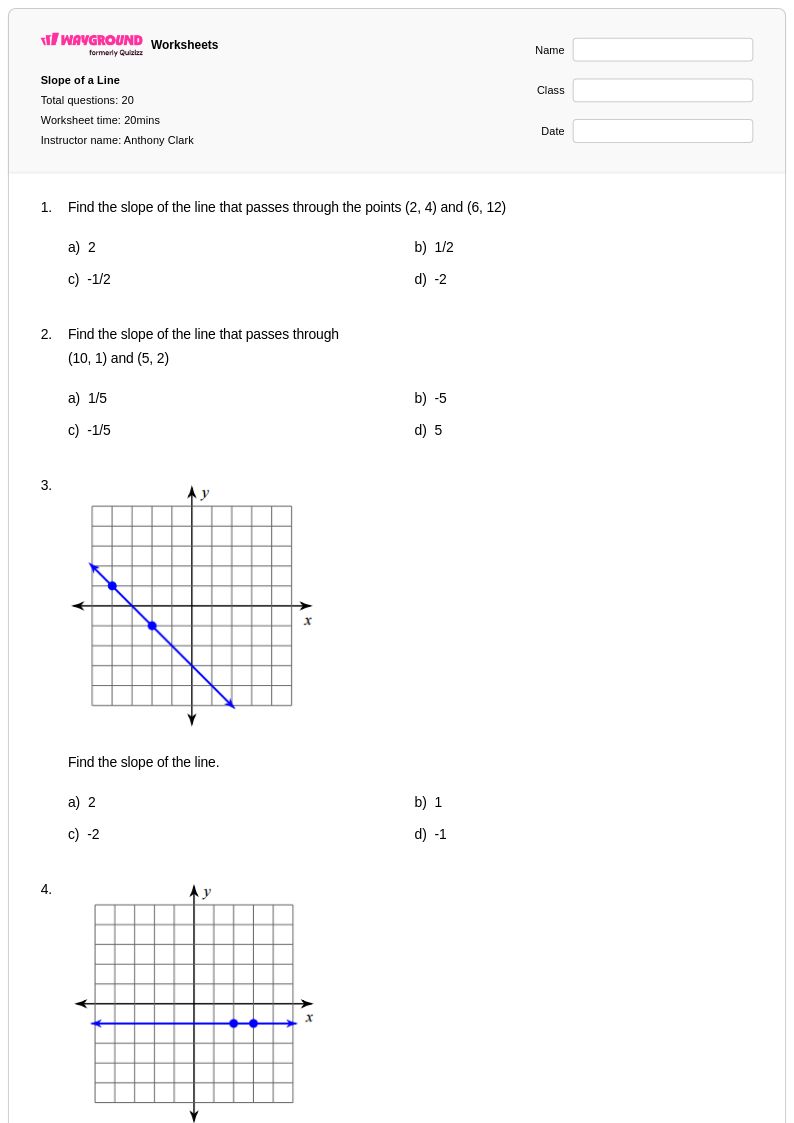
20 คิว
8th - Uni

20 คิว
9th - Uni

20 คิว
8th - Uni

20 คิว
8th - Uni
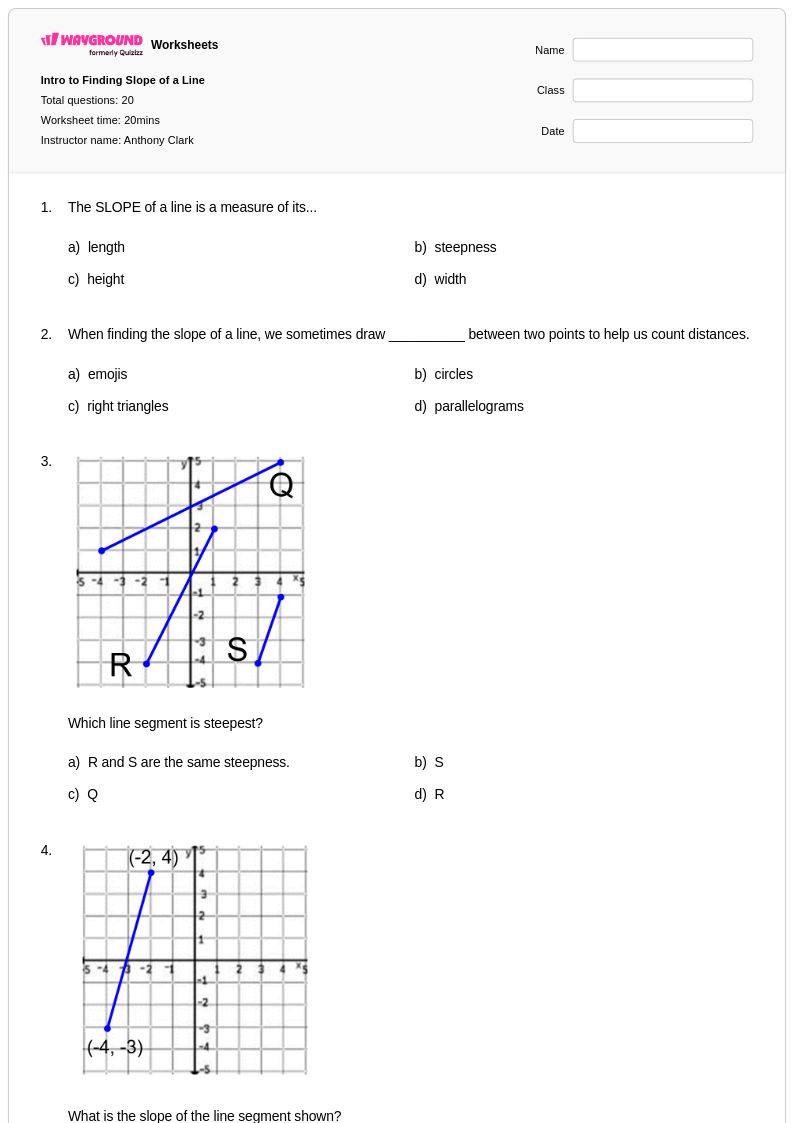
20 คิว
8th - Uni
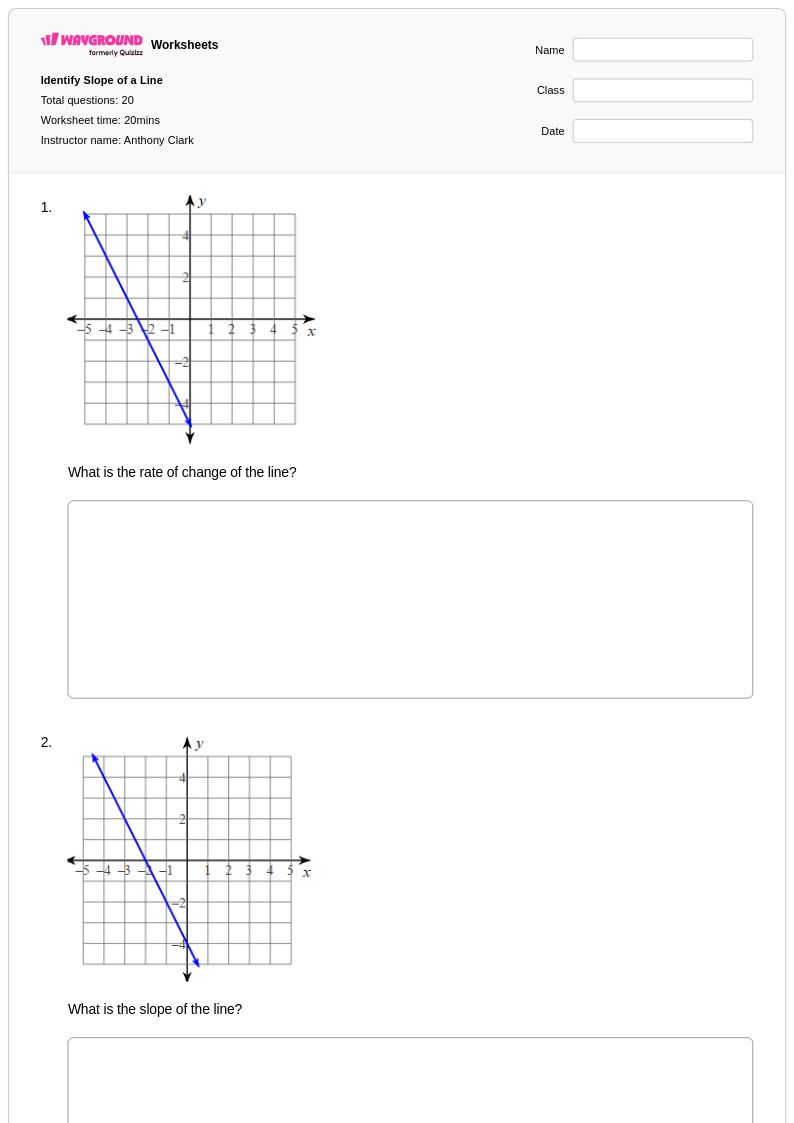
20 คิว
8th - Uni

14 คิว
7th - 12th

20 คิว
8th - Uni

20 คิว
9th - Uni

20 คิว
8th - Uni
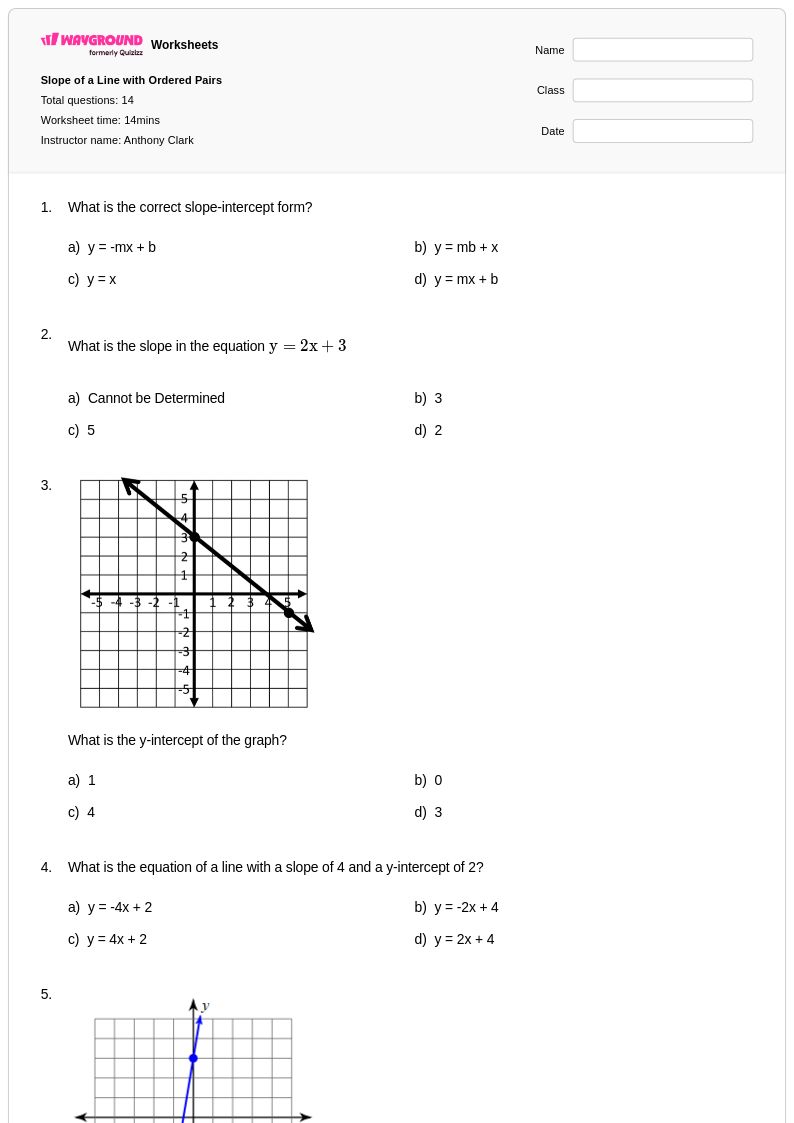
14 คิว
8th - Uni
20 คิว
8th - Uni

20 คิว
8th - Uni

18 คิว
8th - Uni
20 คิว
8th - Uni
28 คิว
9th - 12th
20 คิว
8th - Uni
20 คิว
8th - Uni

20 คิว
8th - Uni
สำรวจใบงานวิชาอื่นๆ สำหรับ ระดับ 12
สำรวจแผ่นงาน ความชันของเส้นตรง ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 12
แบบฝึกหัดเรื่องความชันของเส้นตรงสำหรับนักเรียนชั้นมัธยมศึกษาปีที่ 6 (เกรด 12) จาก Wayground (เดิมคือ Quizizz) ให้แบบฝึกหัดที่ครอบคลุมเกี่ยวกับแนวคิดพื้นฐานนี้ในสมการเชิงเส้น แหล่งข้อมูลที่ออกแบบมาอย่างเชี่ยวชาญเหล่านี้ช่วยให้นักเรียนเชี่ยวชาญในการคำนวณความชันโดยใช้วิธีระยะทางขึ้นหารด้วยระยะทางวิ่ง การตีความความชันว่าเป็นอัตราการเปลี่ยนแปลง และความเข้าใจถึงความสำคัญทางเรขาคณิตของความชันที่เป็นบวก ลบ ศูนย์ และหาค่าไม่ได้ นักเรียนจะได้ทำแบบฝึกหัดที่ต้องหาความชันจากสองจุด การแสดงผลด้วยกราฟ และการประยุกต์ใช้ในโลกแห่งความเป็นจริง ซึ่งจะช่วยสร้างทักษะการวิเคราะห์ที่จำเป็นสำหรับวิชาคณิตศาสตร์ขั้นสูง แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียดและมีให้ดาวน์โหลดฟรีในรูปแบบ PDF ที่สะดวก ช่วยให้นักเรียนพัฒนาความเชี่ยวชาญในการคำนวณความชันและการตีความในบริบททางคณิตศาสตร์ต่างๆ
Wayground (เดิมคือ Quizizz) สนับสนุนครูผู้สอนคณิตศาสตร์ด้วยแบบฝึกหัดเรื่องความชันของเส้นตรงที่สร้างโดยครูหลายล้านชุด ซึ่งช่วยลดความซับซ้อนในการวางแผนการสอนและการประเมินนักเรียน ความสามารถในการค้นหาและการกรองที่มีประสิทธิภาพของแพลตฟอร์มช่วยให้ครูสามารถค้นหาสื่อที่สอดคล้องกับมาตรฐานเกรด 12 ได้อย่างรวดเร็วและปรับการสอนให้เหมาะสมกับความต้องการของนักเรียนแต่ละคน ชุดแบบฝึกหัดที่ปรับแต่งได้เหล่านี้มีให้เลือกทั้งในรูปแบบไฟล์ PDF ที่สามารถพิมพ์ได้ และเวอร์ชันดิจิทัลแบบโต้ตอบ ทำให้สามารถนำไปใช้ได้อย่างยืดหยุ่นในสภาพแวดล้อมห้องเรียนที่หลากหลาย ครูสามารถระบุแหล่งข้อมูลได้อย่างมีประสิทธิภาพสำหรับการฝึกฝนทักษะเฉพาะด้าน การแก้ไขแนวคิดพื้นฐานเกี่ยวกับความชัน หรือกิจกรรมเสริมที่เชื่อมโยงความชันกับการประยุกต์ใช้ในวงกว้างในวิชาแคลคูลัสและการแก้ปัญหาในโลกแห่งความเป็นจริง เพื่อให้มั่นใจว่านักเรียนชั้นมัธยมศึกษาปีที่ 6 ทุกคนจะพัฒนาความเชี่ยวชาญในแนวคิดทางคณิตศาสตร์ที่สำคัญนี้
