
15Q
9th - Uni

34Q
9th - 12th

17Q
10th - Uni

20Q
9th - 12th

20Q
11th - Uni
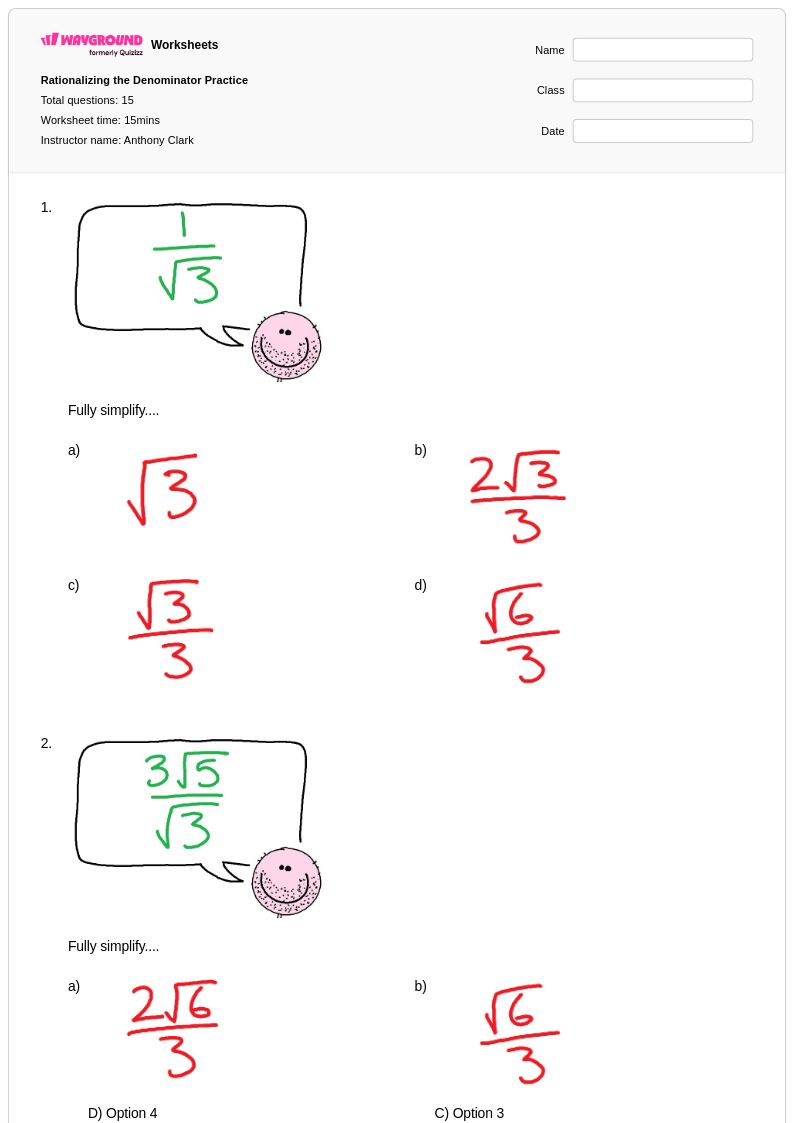
15Q
10th - Uni

14Q
12th

14Q
11th - Uni

17Q
9th - 12th

19Q
9th - 12th

15Q
9th - Uni

9Q
9th - 12th

8Q
7th - Uni

12Q
9th - 12th

6Q
8th - 12th
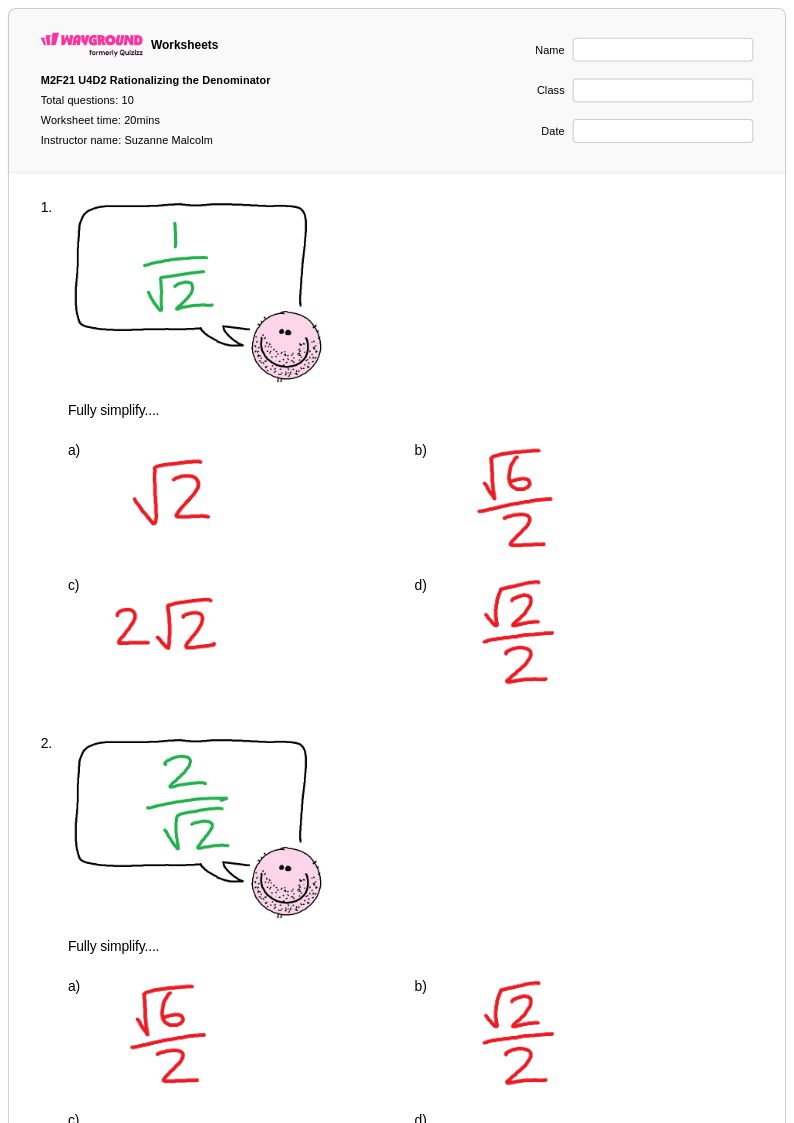
10Q
9th - 12th

20Q
10th - Uni

15Q
11th - Uni

15Q
10th - Uni

20Q
10th - Uni

16Q
9th - Uni

10Q
11th - Uni

18Q
9th - Uni

25Q
12th - Uni
Explore otras hojas de trabajo de materias para ระดับ 12
สำรวจแผ่นงาน การหาเหตุผลให้กับตัวหาร ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 12
การทำให้ตัวส่วนเป็นจำนวนตรรกยะเป็นทักษะทางพีชคณิตพื้นฐานที่นักเรียนชั้นมัธยมศึกษาปีที่ 6 ต้องเชี่ยวชาญเพื่อเตรียมพร้อมสำหรับวิชาคณิตศาสตร์ขั้นสูงและการประเมินมาตรฐาน ชุดแบบฝึกหัดการทำให้ตัวส่วนเป็นจำนวนตรรกยะที่ครอบคลุมของ Wayground ช่วยให้นักเรียนได้ฝึกฝนอย่างเป็นระบบในการกำจัดรากและนิพจน์ที่ซับซ้อนออกจากตัวส่วนโดยใช้การคูณด้วยตัวประกอบร่วมและการทำให้เป็นจำนวนตรรกยะ แบบฝึกหัดที่จัดทำขึ้นอย่างรอบคอบเหล่านี้จะนำทางนักเรียนผ่านสถานการณ์ที่ท้าทายขึ้นเรื่อยๆ ตั้งแต่ตัวส่วนที่เป็นรากที่สองอย่างง่ายไปจนถึงนิพจน์ที่ซับซ้อนซึ่งเกี่ยวข้องกับรากอันดับสูงและตัวส่วนที่เป็นทวินาม แบบฝึกหัดแต่ละชุดมีเฉลยโดยละเอียดที่ช่วยให้นักเรียนตรวจสอบงานของตนเองและเข้าใจกระบวนการทำให้เป็นจำนวนตรรกยะทีละขั้นตอน ในขณะที่รูปแบบ PDF ที่พิมพ์ได้ฟรีช่วยให้เข้าถึงได้ทั้งสำหรับการเรียนการสอนในห้องเรียนและการเรียนรู้ด้วยตนเอง
คลังทรัพยากรที่สร้างโดยครูผู้สอนจำนวนมากของ Wayground ช่วยให้ครูผู้สอนสามารถสอนการทำให้ตัวส่วนเป็นจำนวนตรรกยะได้อย่างตรงเป้าหมายผ่านแบบฝึกหัดและสื่อการฝึกฝนคุณภาพสูงนับล้านรายการ แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองขั้นสูง ช่วยให้ครูสามารถค้นหาเนื้อหาที่เหมาะสมกับวัยและสอดคล้องกับมาตรฐานคณิตศาสตร์ระดับชั้นมัธยมศึกษาปีที่ 6 ได้อย่างรวดเร็ว ในขณะที่เครื่องมือปรับระดับความยากง่ายในตัวช่วยสนับสนุนความต้องการการเรียนรู้ที่หลากหลายภายในห้องเรียน ครูสามารถปรับแต่งแบบฝึกหัดที่มีอยู่แล้วหรือสร้างสื่อใหม่เพื่อแก้ไขช่องว่างทักษะเฉพาะด้านได้อย่างราบรื่น ไม่ว่าจะเป็นการเน้นเทคนิคการหาจำนวนตรรกยะขั้นพื้นฐานหรือการประยุกต์ใช้ขั้นสูงที่เกี่ยวข้องกับเศษส่วนที่ซับซ้อน ตัวเลือกการส่งมอบที่ยืดหยุ่น รวมถึงรูปแบบ PDF ที่พิมพ์ได้และเวอร์ชันดิจิทัลแบบโต้ตอบ ช่วยให้การวางแผนบทเรียนมีประสิทธิภาพ ในขณะเดียวกันก็สนับสนุนการแก้ไขปัญหาสำหรับนักเรียนที่ประสบปัญหาและโอกาสในการเสริมสร้างความรู้สำหรับผู้เรียนขั้นสูงที่ต้องการเสริมสร้างทักษะการจัดการพีชคณิตของตนเอง
