![[8] Cechy przystawania trójkątów - Có thể in Przystawanie-trójkątów-równoramiennych-i-równobocznych Karty-pracy Klasa 11 - Quizizz](https://quizizz-static.s3.amazonaws.com/_media/worksheets-new/65bfc9414f4f362db084f34b-[8]-cechy-przystawania-trójkątów)
10 Hỏi
8th - Uni

15 Hỏi
8th - Uni

20 Hỏi
9th - 12th
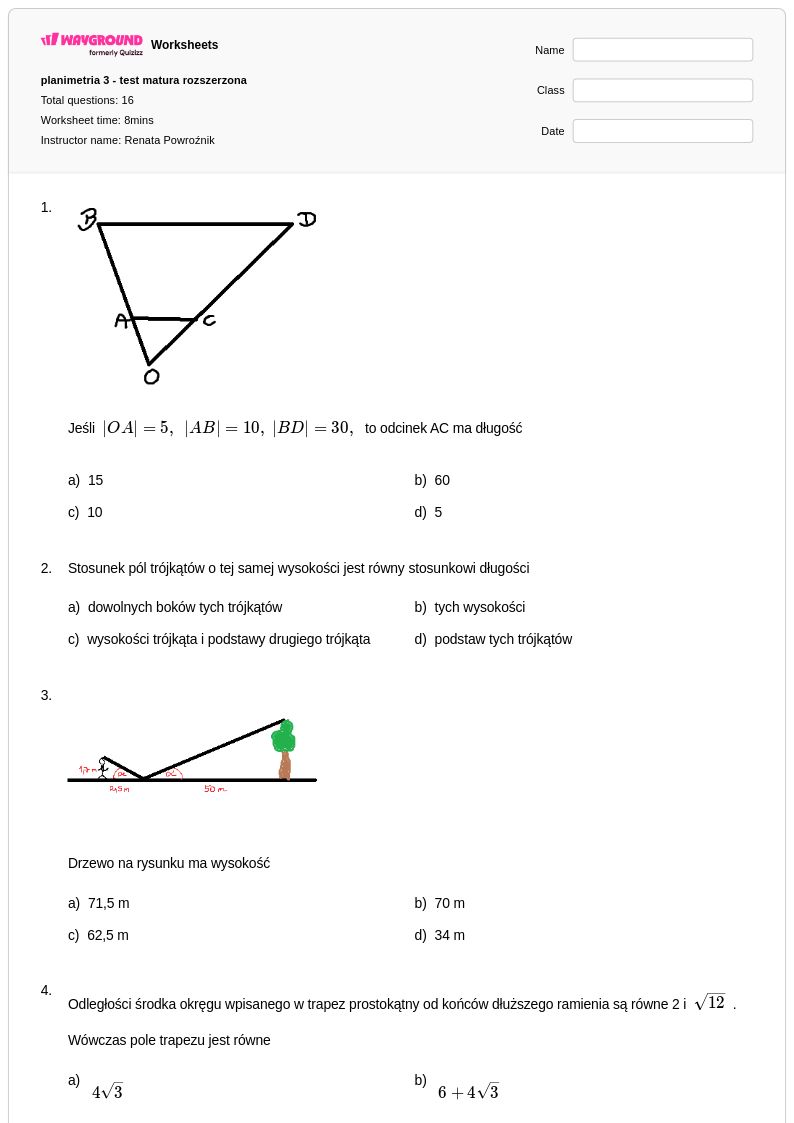
16 Hỏi
10th - 11th
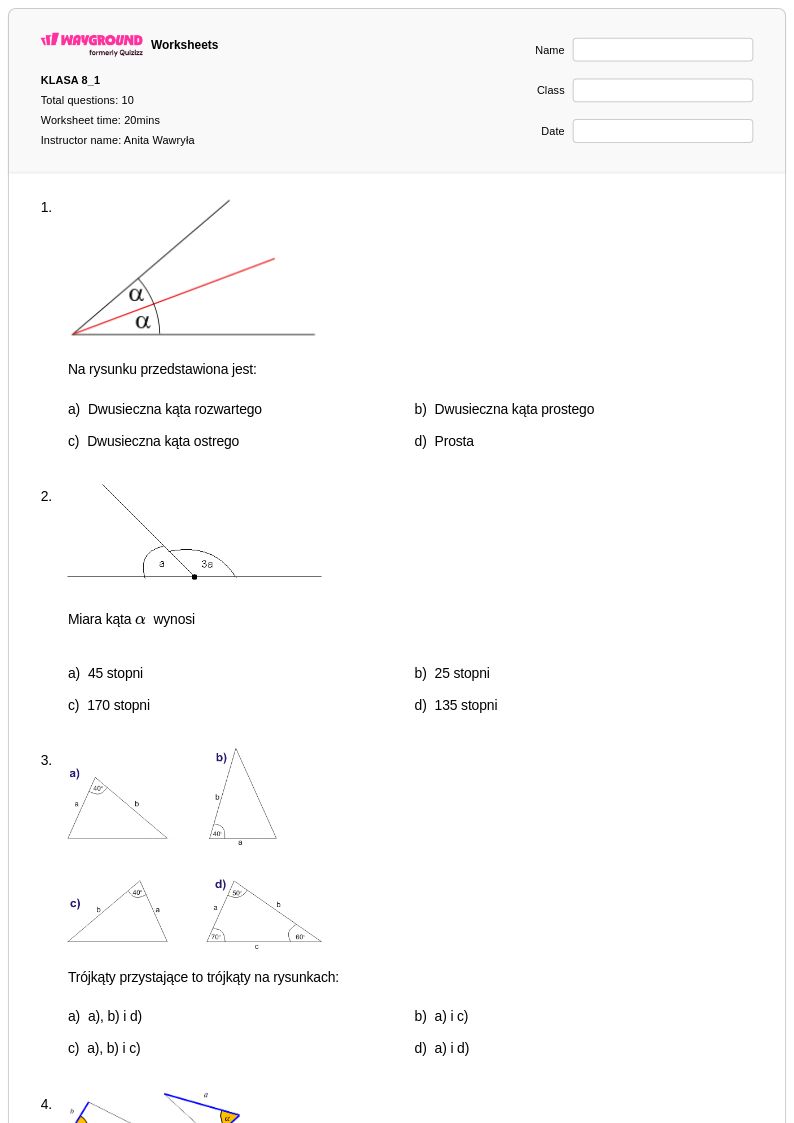
10 Hỏi
1st - PD

18 Hỏi
9th - 12th

13 Hỏi
7th - Uni
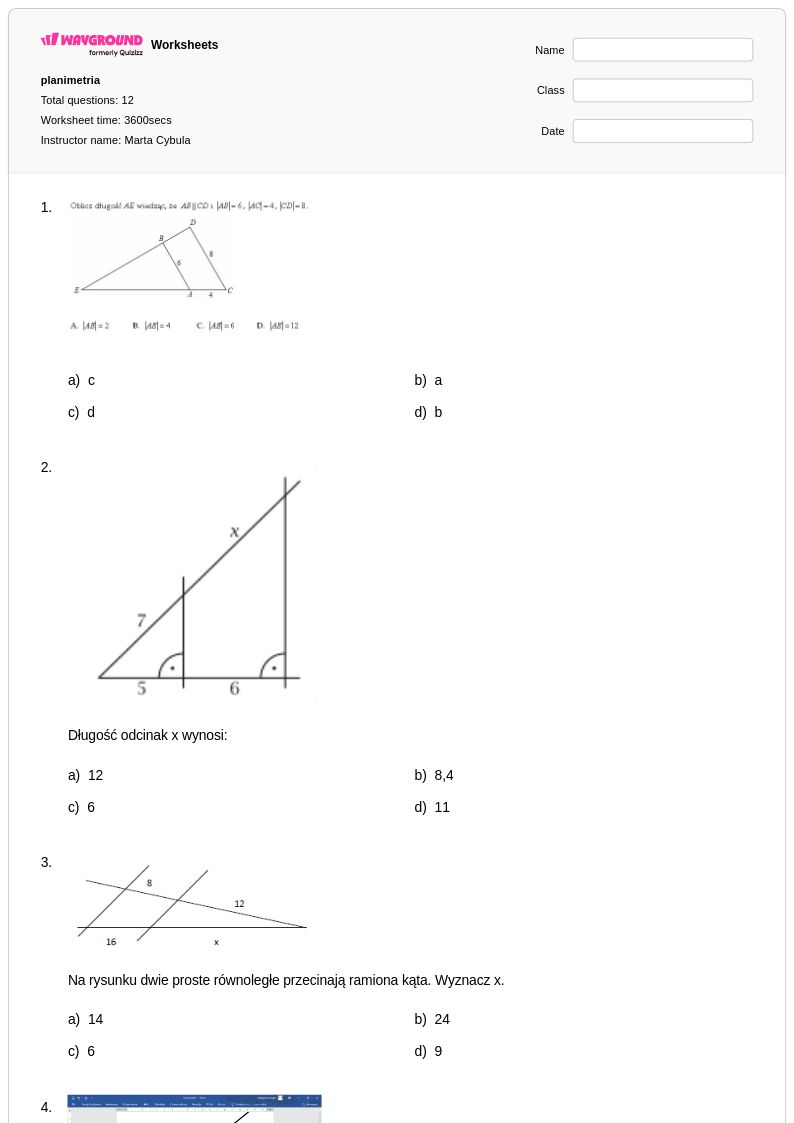
12 Hỏi
11th

15 Hỏi
11th

16 Hỏi
11th

10 Hỏi
4th - 11th

15 Hỏi
1st - Uni

5 Hỏi
11th

6 Hỏi
9th - 12th

20 Hỏi
5th - Uni

14 Hỏi
8th - 12th

6 Hỏi
9th - 12th

8 Hỏi
1st - 12th

21 Hỏi
9th - 12th

19 Hỏi
9th - 12th

17 Hỏi
KG - Uni

25 Hỏi
5th - 12th

8 Hỏi
1st - Uni

14 Hỏi
5th - Uni
Khám phá Przystawanie trójkątów równoramiennych i równobocznych Bảng tính theo cấp độ
Khám phá các bảng tính chủ đề khác cho klasa 11
Przeglądaj arkusze Przystawanie trójkątów równoramiennych i równobocznych do wydrukowania dla Klasa 11
Przystawanie trójkątów równoramiennych i równobocznych stanowi fundamentalną koncepcję geometrii w klasie 11, która opiera się na zrozumieniu przez uczniów własności trójkątów i technik dowodzenia geometrycznego. Obszerny zbiór arkuszy ćwiczeń Wayground koncentruje się na pomocy uczniom w opanowaniu unikalnych zależności przystawania występujących w tych szczególnych trójkątach, w tym twierdzenia o kątach przy podstawie dla trójkątów równoramiennych oraz własności trójkątów równobocznych, w których wszystkie kąty i boki są przystające. Te starannie opracowane zadania praktyczne wzmacniają umiejętność uczniów identyfikowania przystających odcinków i kątów, stosowania zwrotnych, symetrycznych i przechodnich własności przystawania oraz konstruowania formalnych dowodów geometrycznych z wykorzystaniem tych specjalistycznych zależności trójkątów. Każdy arkusz ćwiczeń zawiera szczegółowy klucz odpowiedzi i jest dostępny w darmowym pliku PDF do wydruku, umożliwiając uczniom rozwiązywanie coraz bardziej złożonych problemów, rozwijając ich umiejętności rozumowania przestrzennego i logicznego myślenia, niezbędne na zaawansowanych kursach geometrii.
Wayground, dawniej Quizizz, oferuje nauczycielom bogatą bibliotekę milionów zasobów stworzonych przez nauczycieli, specjalnie zaprojektowanych do wspierania nauczania geometrii na poziomie 11. klasy. Zaawansowane funkcje wyszukiwania i filtrowania platformy pozwalają nauczycielom szybko znaleźć arkusze ćwiczeń zgodne z określonymi standardami programowymi i precyzyjnie ukierunkować koncepcje zgodności, które ich uczniowie muszą opanować. Te narzędzia różnicujące pozwalają nauczycielom dostosować poziom trudności treści, zapewniając uczniom mającym trudności odpowiednie wsparcie, a uczniom zaawansowanym – dostęp do materiałów wzbogacających, które podważają ich rozumienie zasad zgodności trójkątów. Dostępne zarówno w formacie do druku, jak i w formacie PDF, zbiory arkuszy ćwiczeń płynnie integrują się z procesami planowania lekcji, oferując elastyczne opcje ćwiczeń w klasie, zadań domowych, przygotowania do oceny oraz ukierunkowanego wzmacniania umiejętności, które odpowiadają indywidualnym potrzebom edukacyjnym w zakresie rozumowania geometrycznego i konstruowania dowodów.
