
11Q
9th - 12th

25Q
9th - 12th
14Q
10th - Uni

13Q
9th - 12th

15Q
9th

20Q
9th - 10th
25Q
8th - 11th

25Q
10th
12Q
10th
12Q
10th - Uni

17Q
10th

18Q
9th

35Q
9th

20Q
9th - Uni
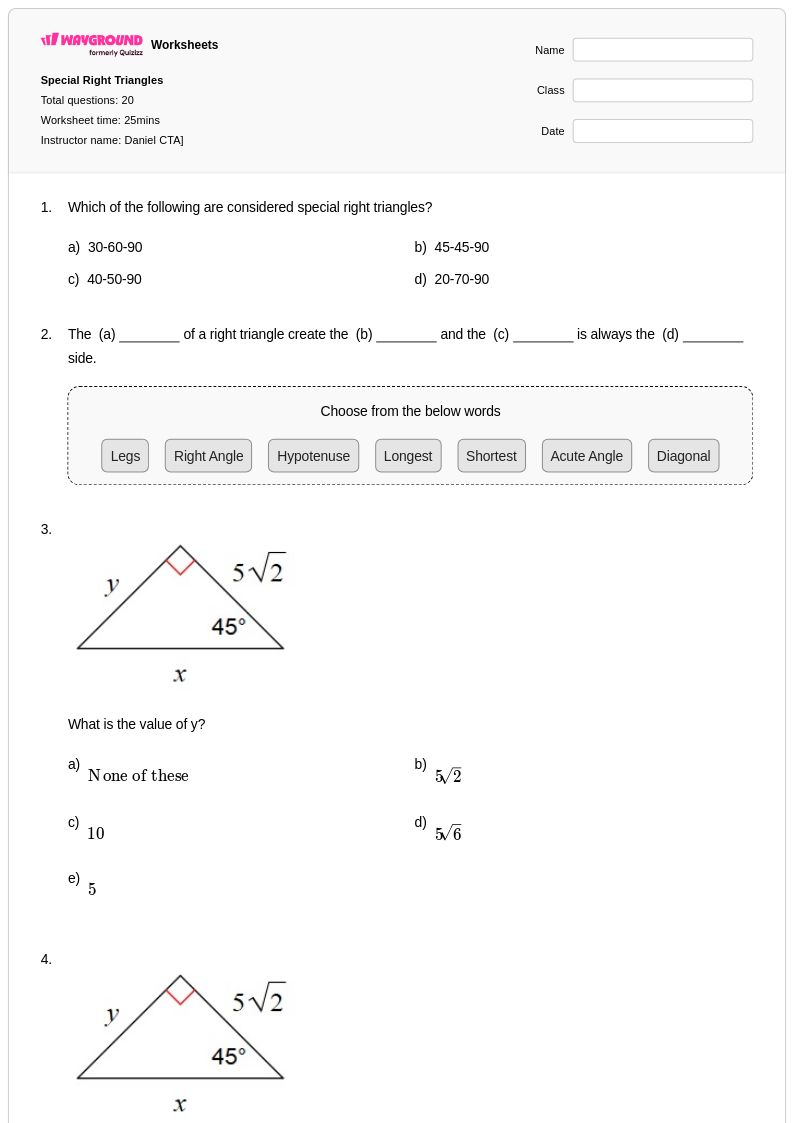
20Q
12th

18Q
9th - 12th
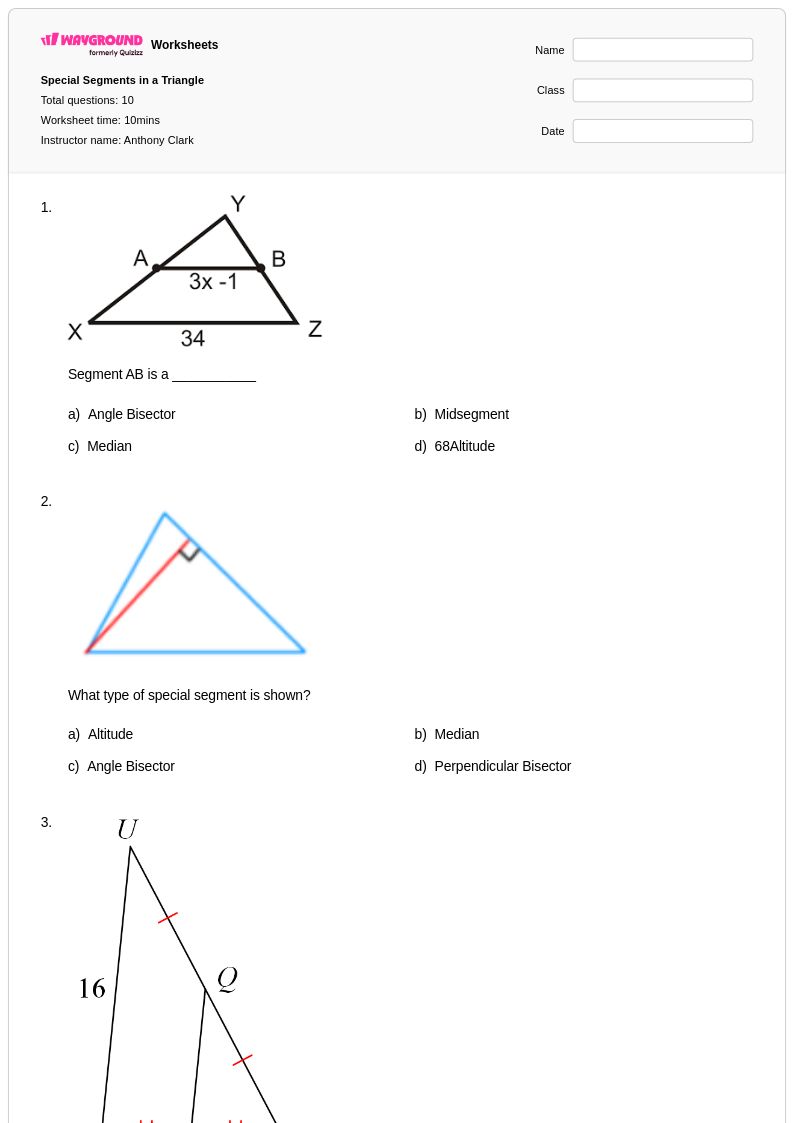
10Q
10th - Uni
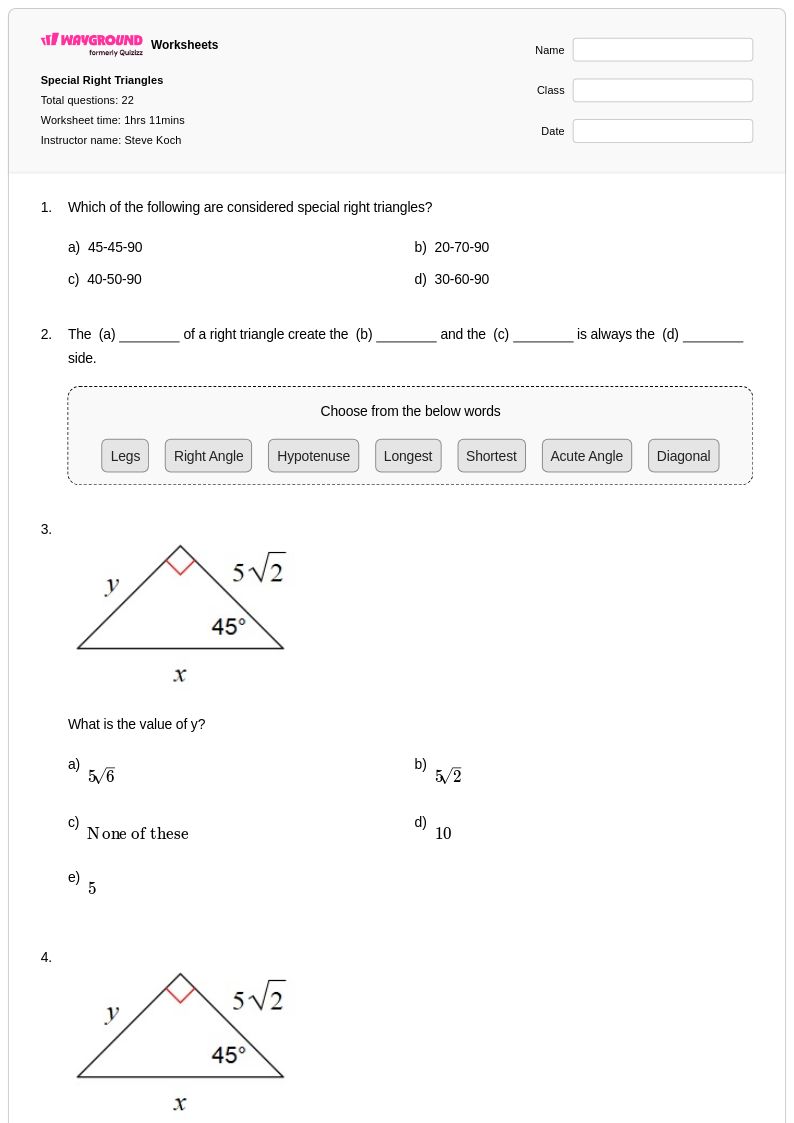
22Q
10th

20Q
10th
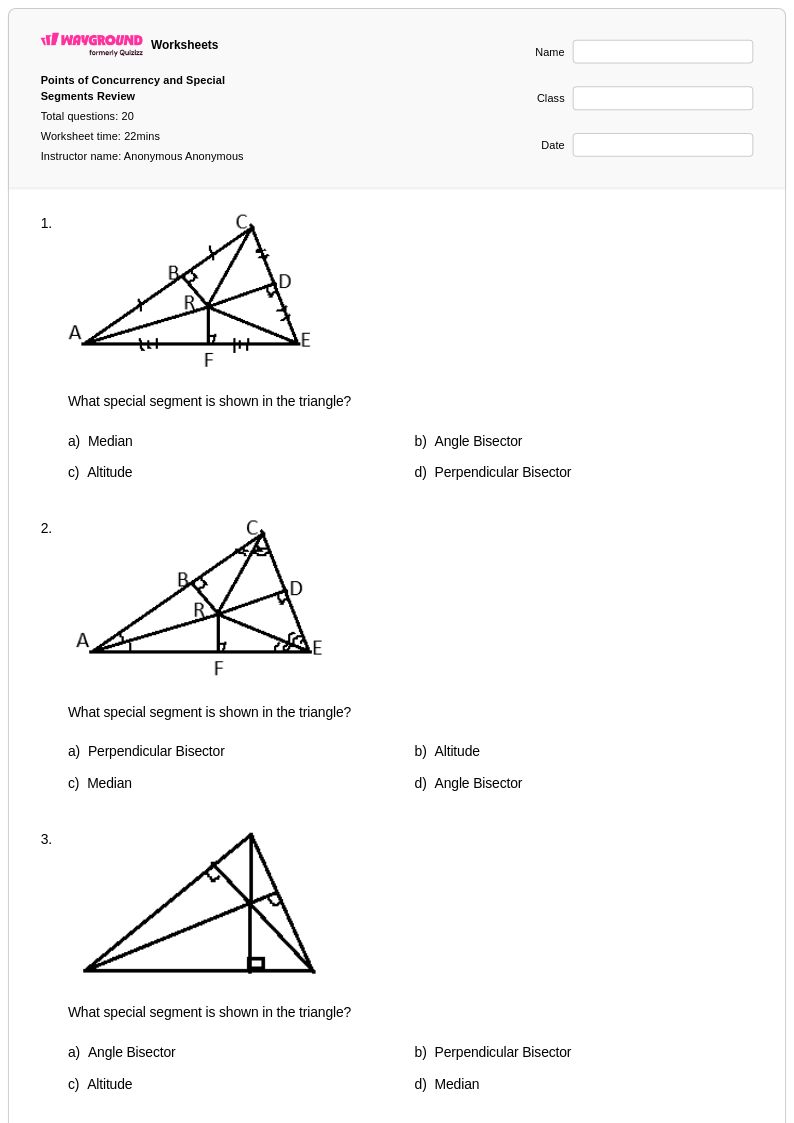
20Q
10th
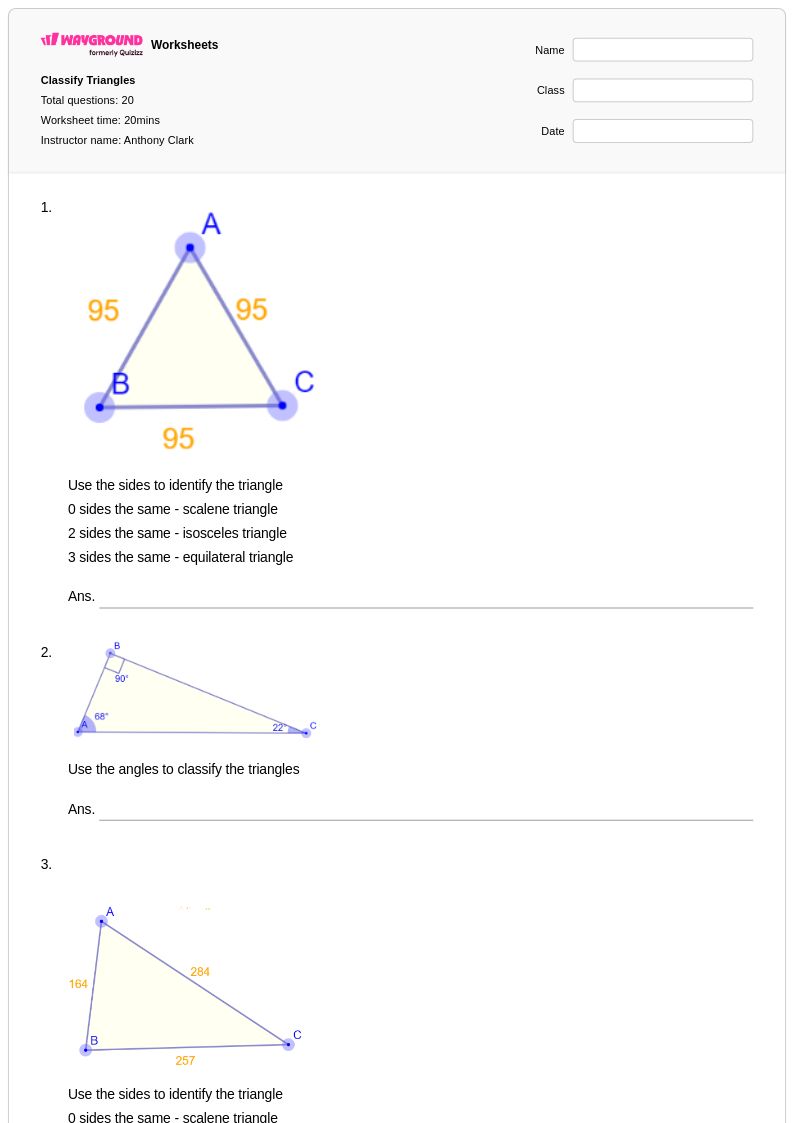
20Q
5th - Uni
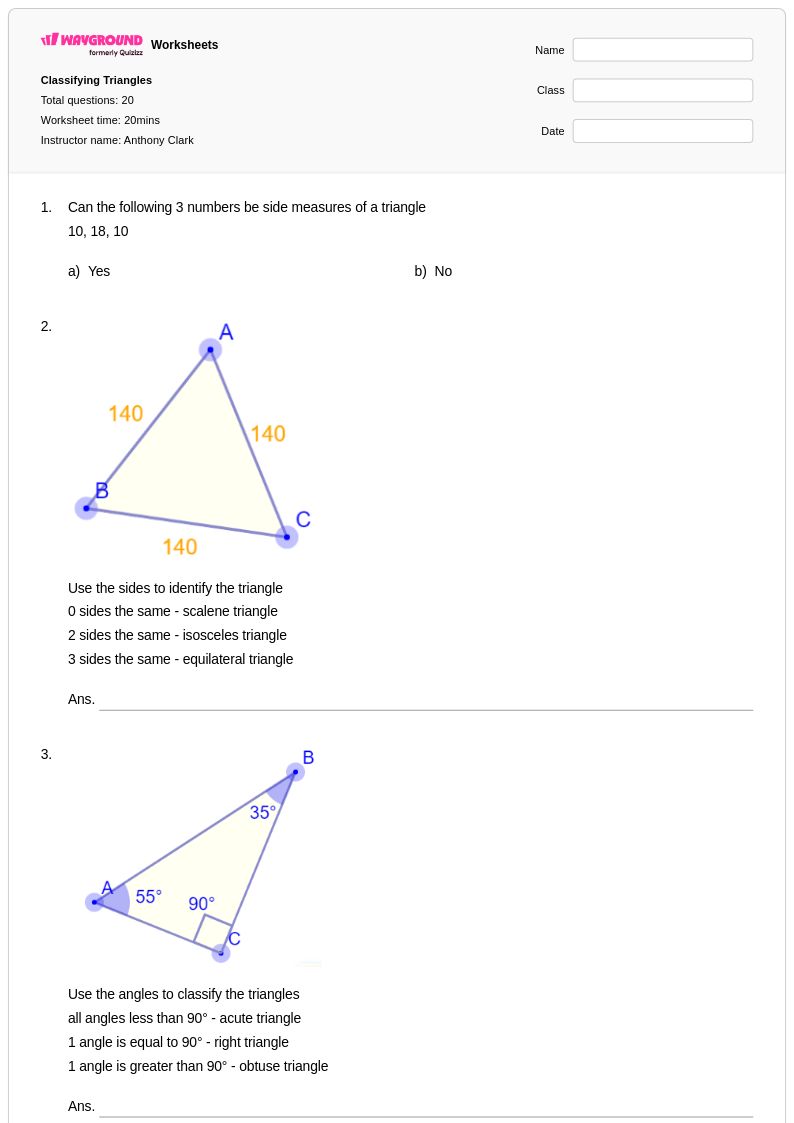
20Q
7th - Uni

15Q
9th
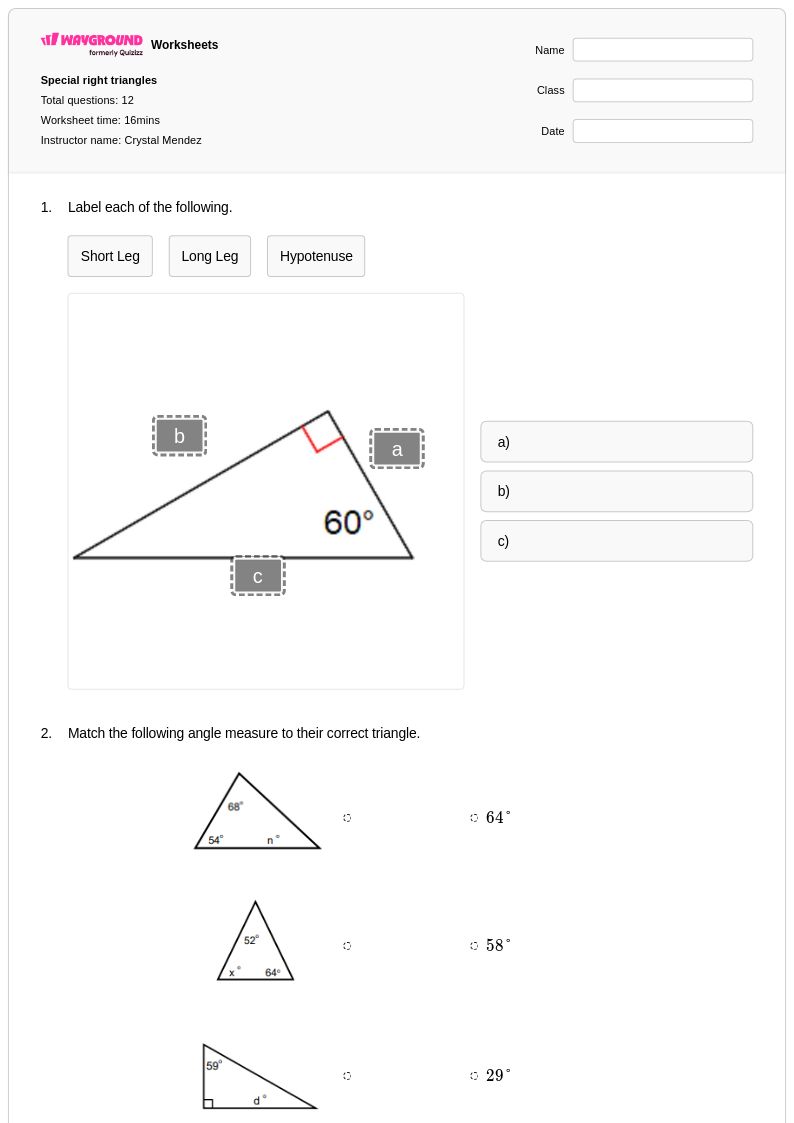
12Q
10th
Explorar hojas de trabajo por materias
สำรวจแผ่นงาน ส่วนพิเศษรูปสามเหลี่ยม ที่พิมพ์ได้
แบบฝึกหัดเกี่ยวกับส่วนพิเศษของสามเหลี่ยมที่มีให้ใช้งานผ่าน Wayground (เดิมคือ Quizizz) ให้แบบฝึกหัดที่ครอบคลุมเกี่ยวกับแนวคิดทางเรขาคณิตพื้นฐานของเส้นมัธยฐาน เส้นความสูง เส้นแบ่งครึ่งมุม และเส้นแบ่งครึ่งตั้งฉากภายในสามเหลี่ยม แหล่งข้อมูลที่สร้างขึ้นอย่างเชี่ยวชาญเหล่านี้ช่วยเสริมสร้างความเข้าใจของนักเรียนเกี่ยวกับวิธีการที่ส่วนพิเศษเหล่านี้ตัดกันที่จุดตัดเฉพาะต่างๆ รวมถึงจุดศูนย์กลางมวล จุดตั้งฉาก จุดศูนย์กลางแนบใน และจุดศูนย์กลางวงกลมล้อมรอบ แบบฝึกหัดเหล่านี้สร้างความเชี่ยวชาญในการคำนวณความยาวส่วน การระบุคุณสมบัติของส่วน และการประยุกต์ใช้ทฤษฎีบทที่เกี่ยวข้องกับองค์ประกอบสำคัญของสามเหลี่ยมเหล่านี้อย่างเป็นระบบ แหล่งข้อมูลแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียดและมีให้ใช้งานในรูปแบบไฟล์ PDF ที่สะดวกต่อการพิมพ์ฟรี โดยมีแบบฝึกหัดที่หลากหลายตั้งแต่แบบฝึกหัดการระบุพื้นฐานไปจนถึงการพิสูจน์ทางเรขาคณิตที่ซับซ้อนซึ่งเกี่ยวข้องกับความสัมพันธ์ของส่วนพิเศษ
Wayground (เดิมคือ Quizizz) สนับสนุนนักการศึกษาคณิตศาสตร์ด้วยชุดแหล่งข้อมูลเกี่ยวกับส่วนพิเศษของสามเหลี่ยมที่สร้างโดยครูผู้สอนจำนวนมาก โดยดึงมาจากสื่อคุณภาพสูงนับล้านรายการที่ผ่านการตรวจสอบอย่างเข้มงวดและสอดคล้องกับมาตรฐานทางเรขาคณิต แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองขั้นสูง ช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่ตรงกับความต้องการเฉพาะด้านของส่วนพิเศษของรูปสามเหลี่ยมได้อย่างรวดเร็ว ไม่ว่าจะเป็นเทคนิคการสร้าง การประยุกต์ใช้เรขาคณิตพิกัด หรือการพิสูจน์ทางทฤษฎี เครื่องมือปรับแต่งที่ยืดหยุ่นช่วยให้ครูสามารถปรับเปลี่ยนสื่อที่มีอยู่ หรือสร้างเวอร์ชันที่แตกต่างกันเพื่อรองรับความต้องการในการเรียนรู้ที่หลากหลาย ในขณะที่รูปแบบไฟล์ PDF ที่พิมพ์ได้และเวอร์ชันดิจิทัลแบบโต้ตอบได้ ช่วยเพิ่มความหลากหลายในการสอนในห้องเรียน การบ้าน และการเตรียมการประเมินผล ทรัพยากรที่ครอบคลุมเหล่านี้ช่วยให้การวางแผนบทเรียนง่ายขึ้น พร้อมทั้งให้การสนับสนุนที่ตรงเป้าหมายสำหรับการแก้ไข การเสริมสร้าง และการพัฒนาทักษะอย่างเป็นระบบในหัวข้อเรขาคณิตที่สำคัญนี้
