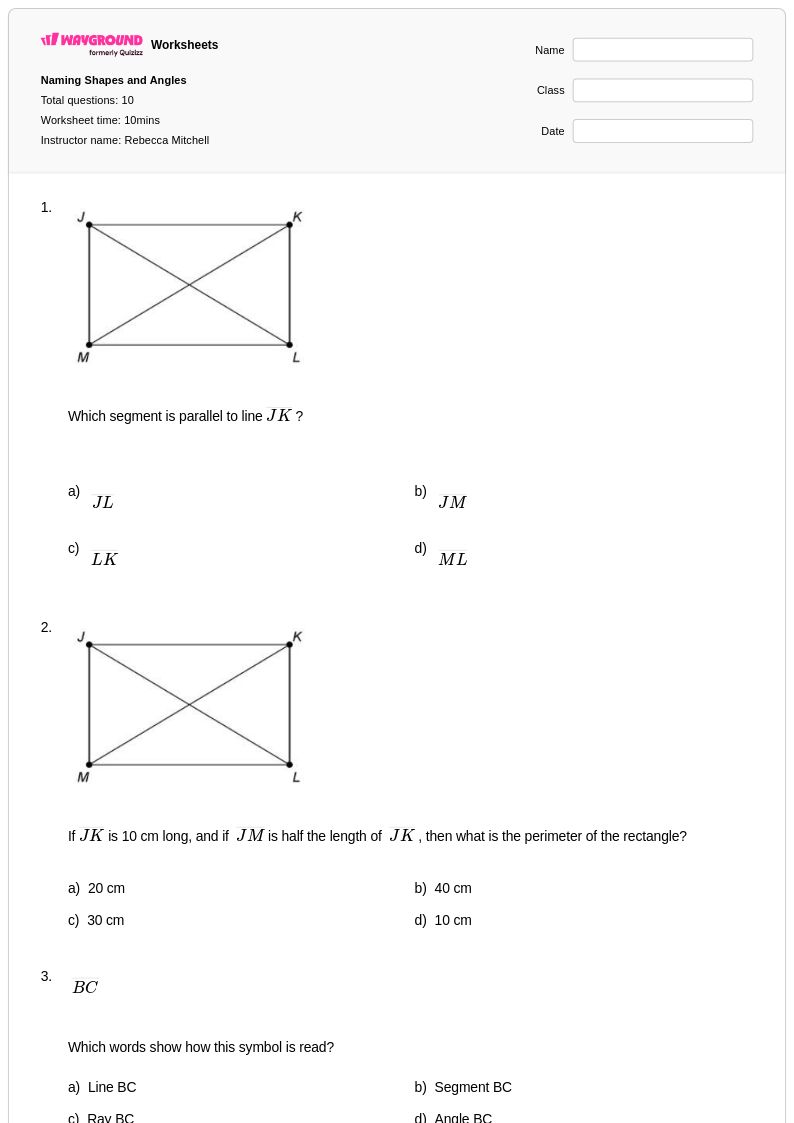
10 คิว
5th
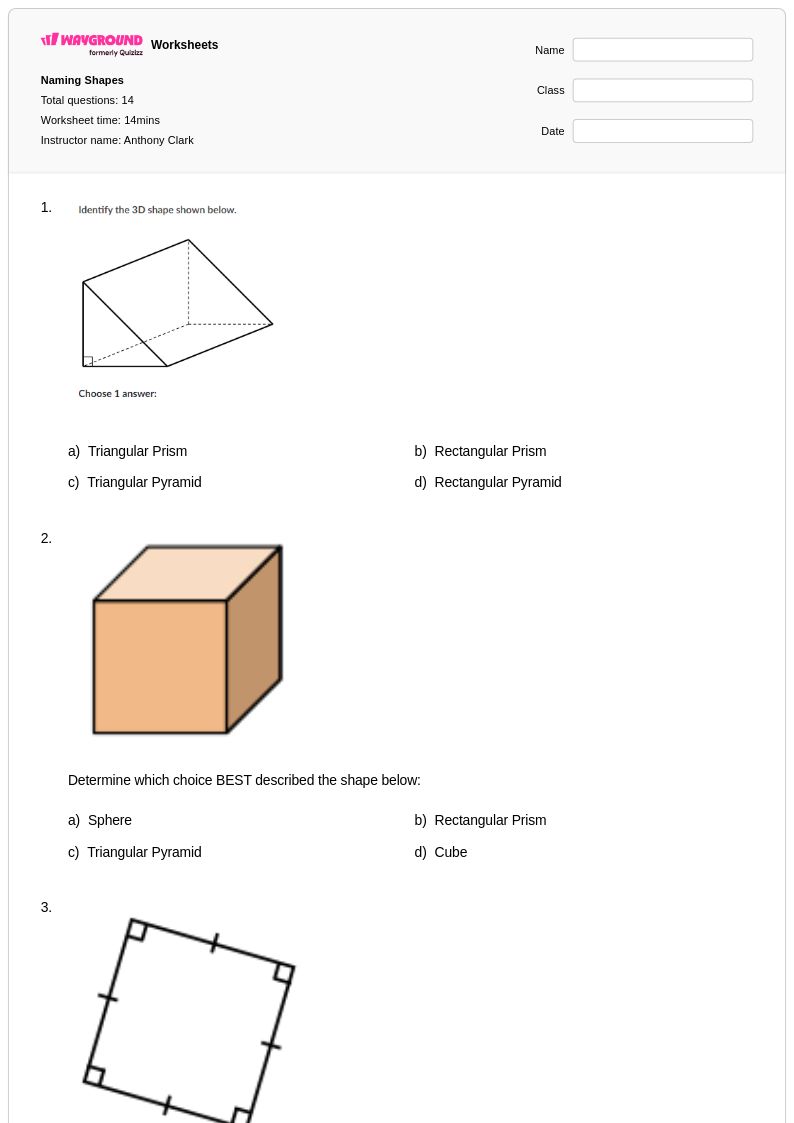
14 คิว
8th - Uni

11 คิว
2nd - Uni

16 คิว
2nd

10 คิว
KG
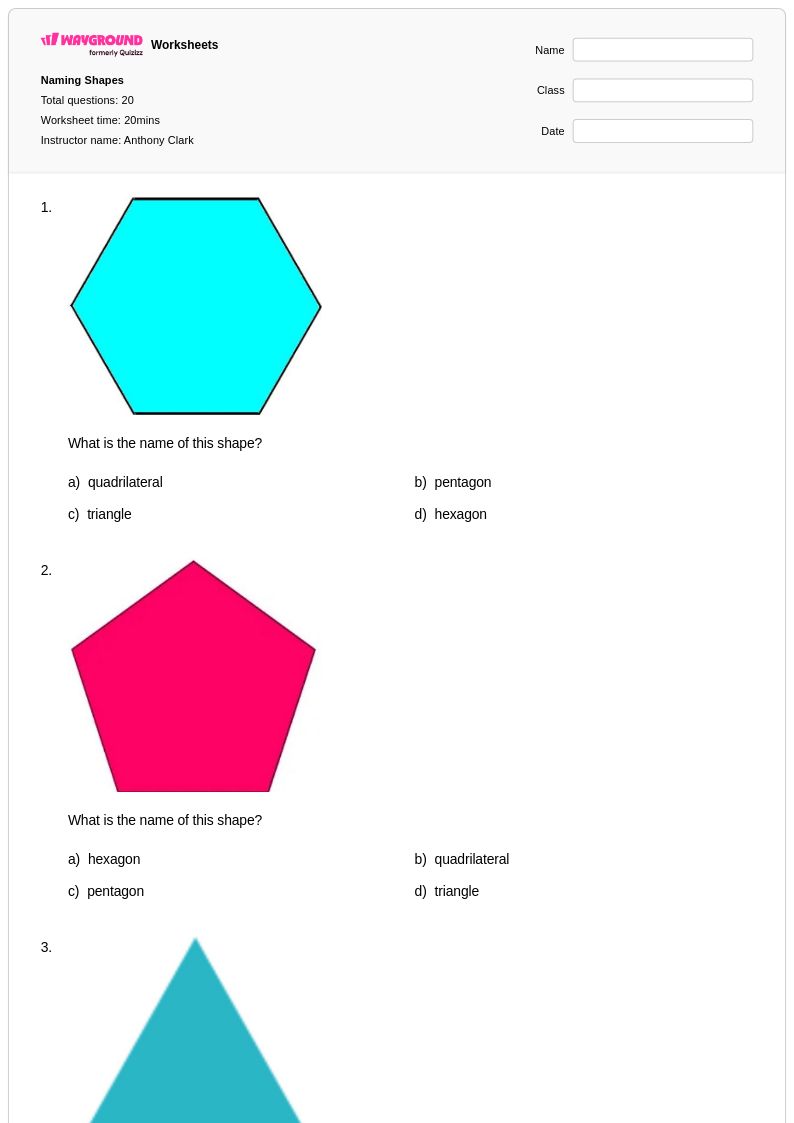
20 คิว
8th

15 คิว
2nd

15 คิว
8th - Uni

10 คิว
2nd - Uni

24 คิว
3rd - 4th

20 คิว
8th - Uni
20 คิว
2nd - Uni

6 คิว
2nd

15 คิว
9th - 12th

37 คิว
2nd
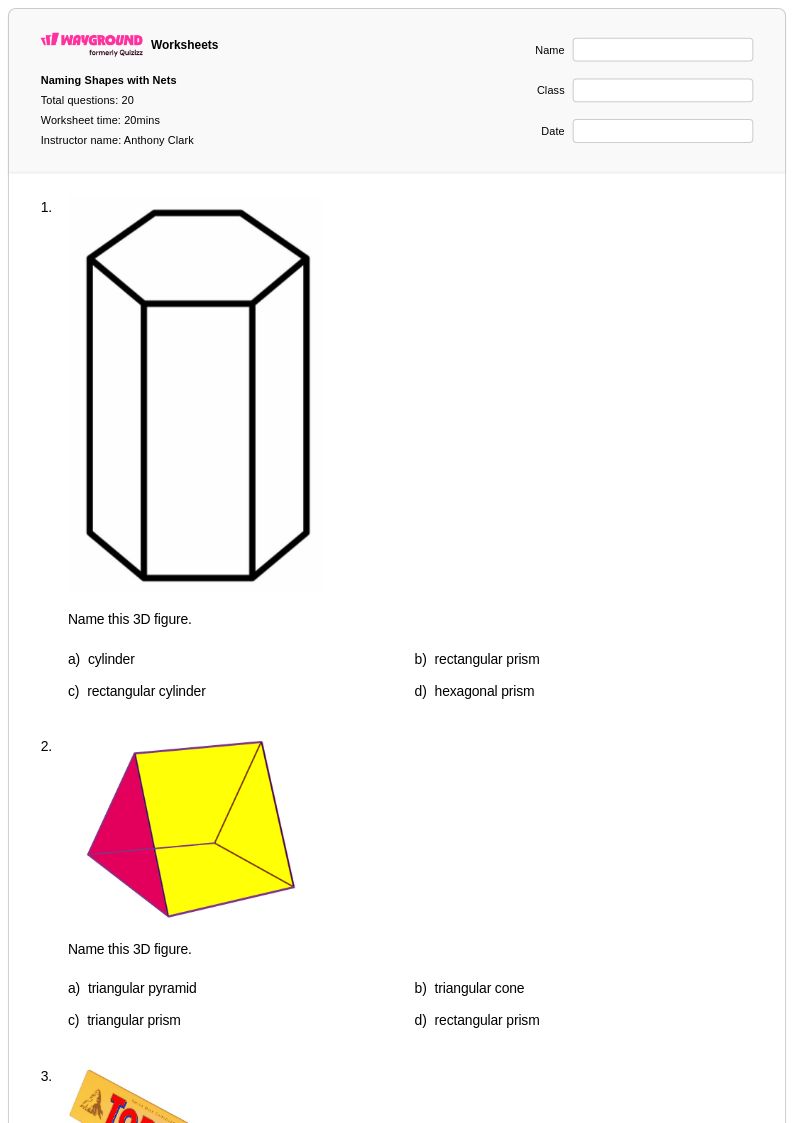
20 คิว
6th - Uni

10 คิว
1st
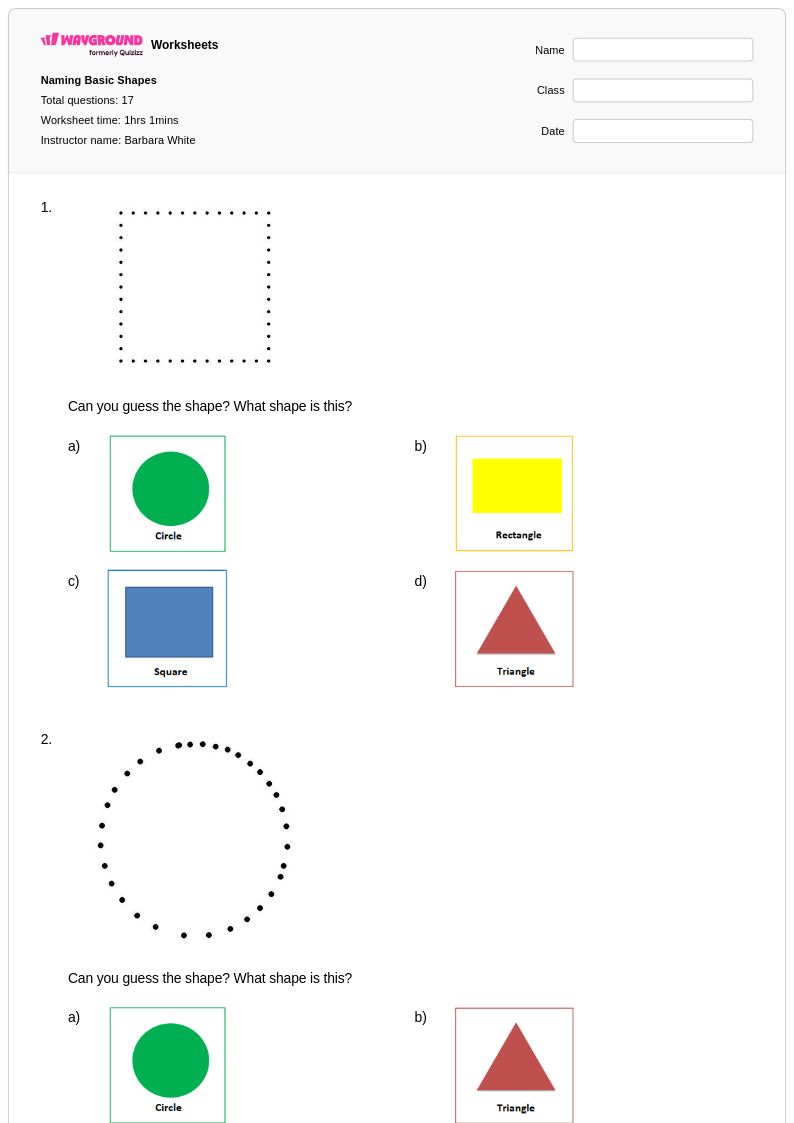
17 คิว
KG - 1st
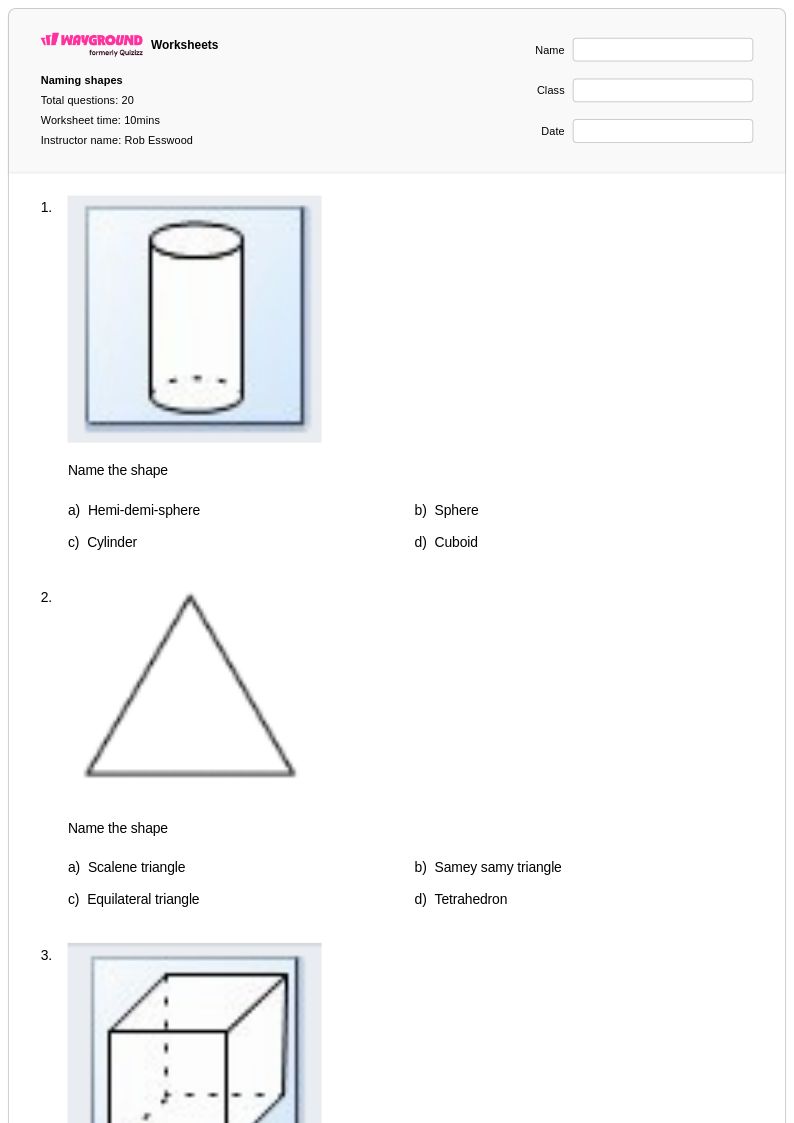
20 คิว
6th - 9th

16 คิว
6th - 8th
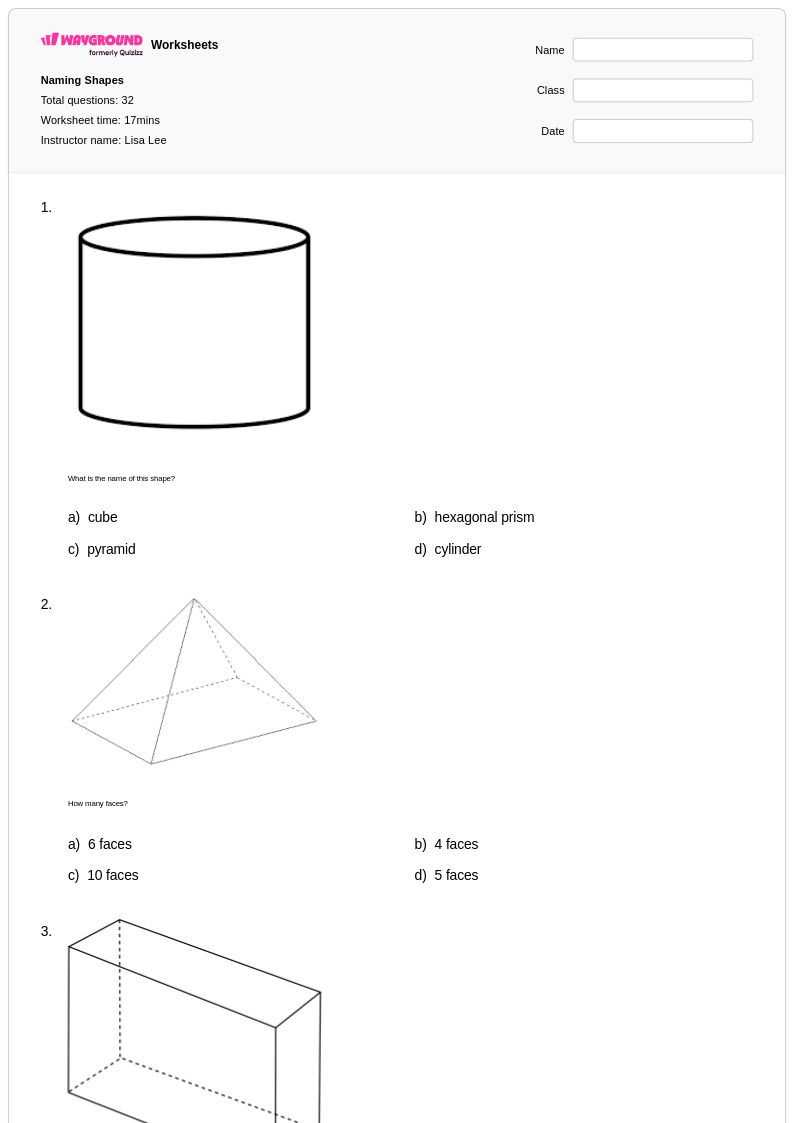
32 คิว
7th
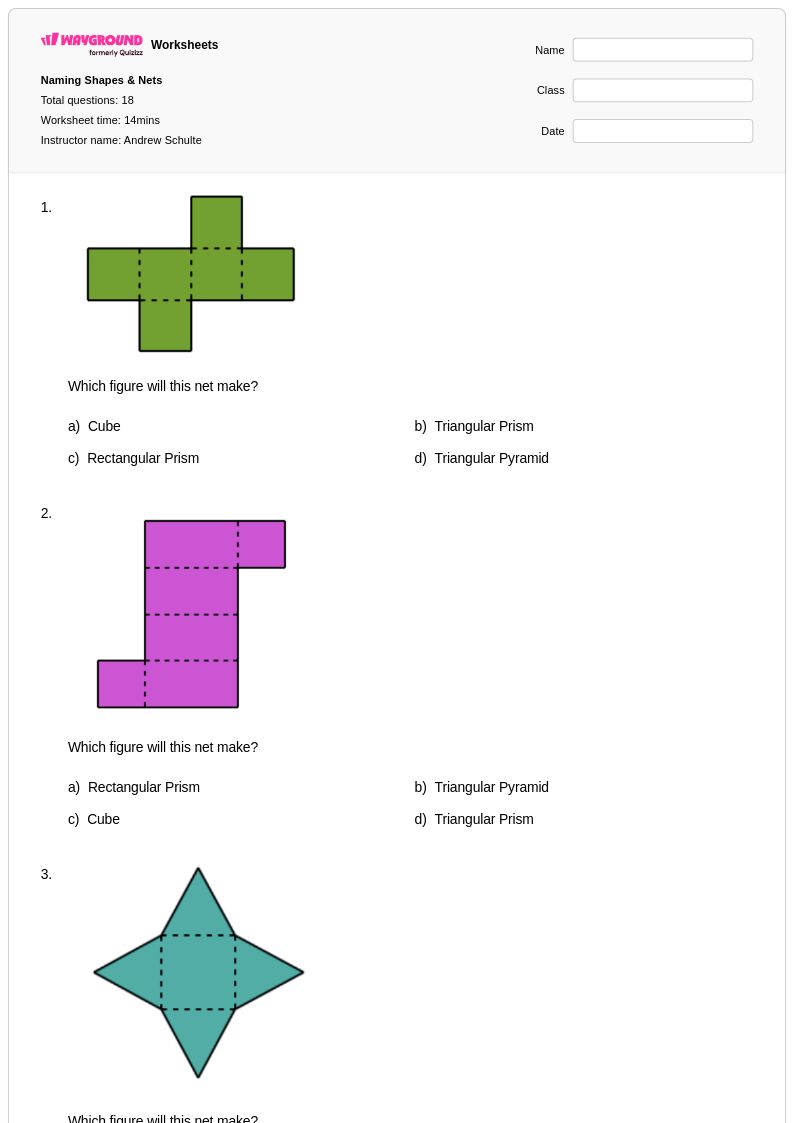
18 คิว
6th

10 คิว
3rd
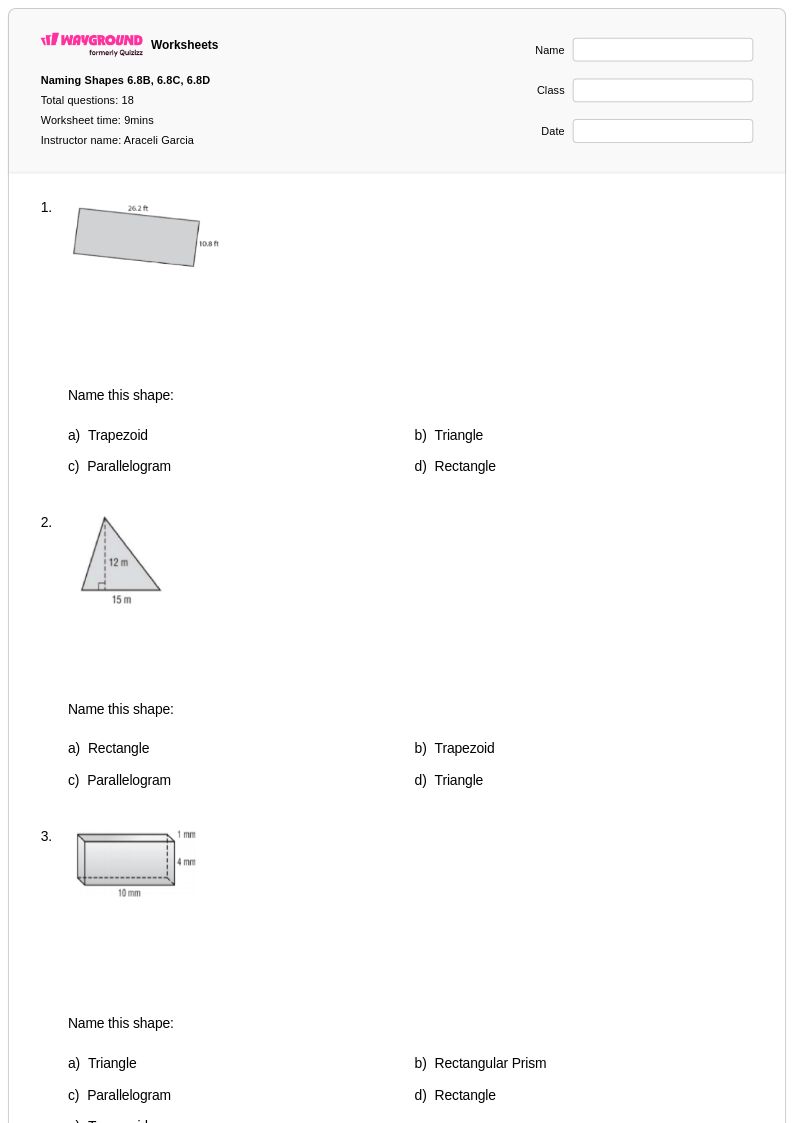
18 คิว
6th
สำรวจแผ่นงานตามเกรด
สำรวจแผ่นงานตามหัวเรื่อง
สำรวจแผ่นงาน การตั้งชื่อรูปทรง ที่พิมพ์ได้
แบบฝึกหัดการตั้งชื่อรูปทรงเรขาคณิตจาก Wayground (เดิมชื่อ Quizizz) ช่วยให้นักเรียนได้ฝึกฝนคำศัพท์ทางเรขาคณิตและทักษะการจดจำภาพ ซึ่งเป็นรากฐานสำคัญของความเข้าใจทางคณิตศาสตร์ แหล่งข้อมูลที่ครอบคลุมเหล่านี้ช่วยให้ผู้เรียนระบุ จำแนก และแยกแยะรูปทรงเรขาคณิตสองมิติและสามมิติต่างๆ ได้ รวมถึงสามเหลี่ยม สี่เหลี่ยม วงกลม รูปหลายเหลี่ยม ทรงกลม ลูกบาศก์ และพีระมิด แบบฝึกหัดแต่ละแผ่นมีโจทย์ฝึกฝนที่ออกแบบมาอย่างพิถีพิถัน ซึ่งจะค่อยๆ พัฒนาความสามารถของนักเรียนในการจดจำคุณลักษณะของรูปทรง เช่น จำนวนด้าน มุม และจุดยอด พร้อมทั้งเสริมสร้างคำศัพท์ทางคณิตศาสตร์ที่ถูกต้อง ครูสามารถเข้าถึงเฉลยคำตอบและสื่อสิ่งพิมพ์ฟรีในรูปแบบ PDF ที่สะดวก ทำให้ง่ายต่อการนำแหล่งข้อมูลเหล่านี้ไปใช้ทั้งในการสอนในห้องเรียนและการเรียนรู้ด้วยตนเอง
คอลเลกชันที่กว้างขวางของ Wayground รวบรวมจากแหล่งข้อมูลที่สร้างโดยครูหลายล้านรายการ โดยเน้นเฉพาะการระบุรูปทรงและการพัฒนาคำศัพท์ทางเรขาคณิต ทำให้ครูผู้สอนมีฟังก์ชันการค้นหาและการกรองที่มีประสิทธิภาพ เพื่อค้นหาแบบฝึกหัดที่ตรงกับความต้องการในการสอนของตนได้อย่างแม่นยำ สื่อการเรียนการสอนของแพลตฟอร์มนี้สอดคล้องกับมาตรฐาน และสนับสนุนการสอนแบบแยกแยะความแตกต่างผ่านเนื้อหาที่ปรับแต่งได้ ซึ่งสามารถปรับเปลี่ยนให้เหมาะสมกับระดับทักษะต่างๆ เพื่อให้มั่นใจได้ว่าทั้งนักเรียนที่เรียนรู้ช้าและนักเรียนที่เรียนรู้เร็วจะได้รับความท้าทายที่เหมาะสม ครูผู้สอนจะได้รับประโยชน์จากตัวเลือกการจัดรูปแบบที่ยืดหยุ่น ซึ่งรวมถึงทั้งเวอร์ชัน PDF ที่พิมพ์ได้สำหรับกิจกรรมแบบใช้กระดาษและดินสอแบบดั้งเดิม และรูปแบบดิจิทัลสำหรับสภาพแวดล้อมการเรียนรู้ที่ใช้เทคโนโลยี เครื่องมืออเนกประสงค์เหล่านี้ช่วยให้การวางแผนบทเรียนง่ายขึ้น ในขณะเดียวกันก็มีแหล่งข้อมูลที่ตรงเป้าหมายสำหรับการแก้ไข การเสริมสร้าง และการฝึกฝนทักษะอย่างต่อเนื่อง ช่วยให้ครูผู้สอนสามารถสร้างความสามารถในการให้เหตุผลทางเรขาคณิตของนักเรียนอย่างเป็นระบบผ่านโอกาสในการฝึกฝนที่มีคุณภาพสูงอย่างสม่ำเสมอ
