18 Hỏi
8th

15 Hỏi
PD

16 Hỏi
5th
34 Hỏi
4th
12 Hỏi
6th
20 Hỏi
6th
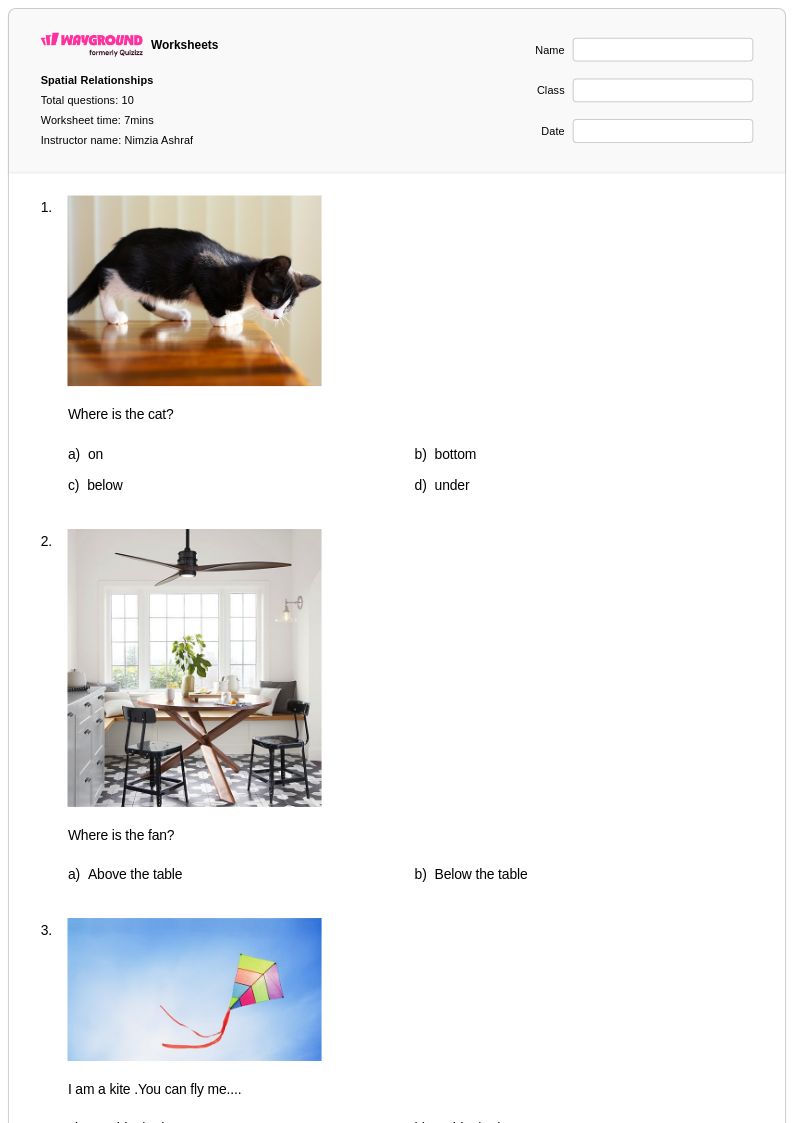
10 Hỏi
KG
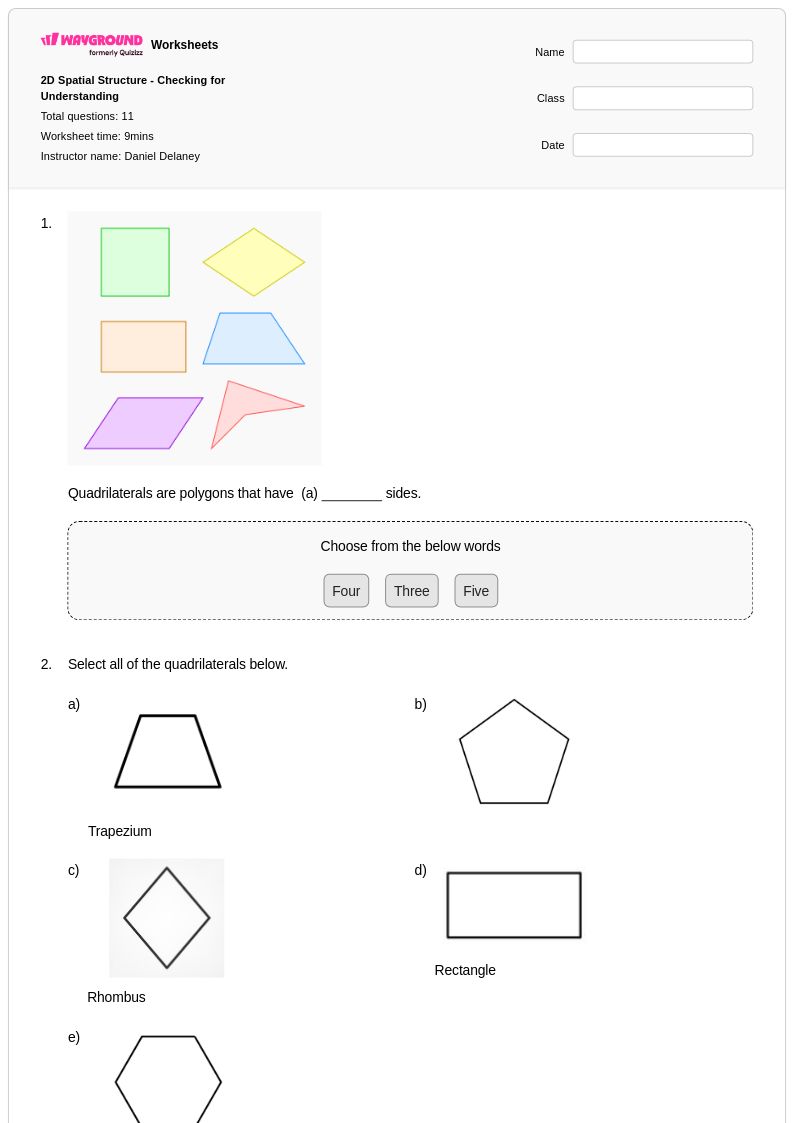
11 Hỏi
6th - Uni

18 Hỏi
9th

20 Hỏi
11th

19 Hỏi
5th - Uni
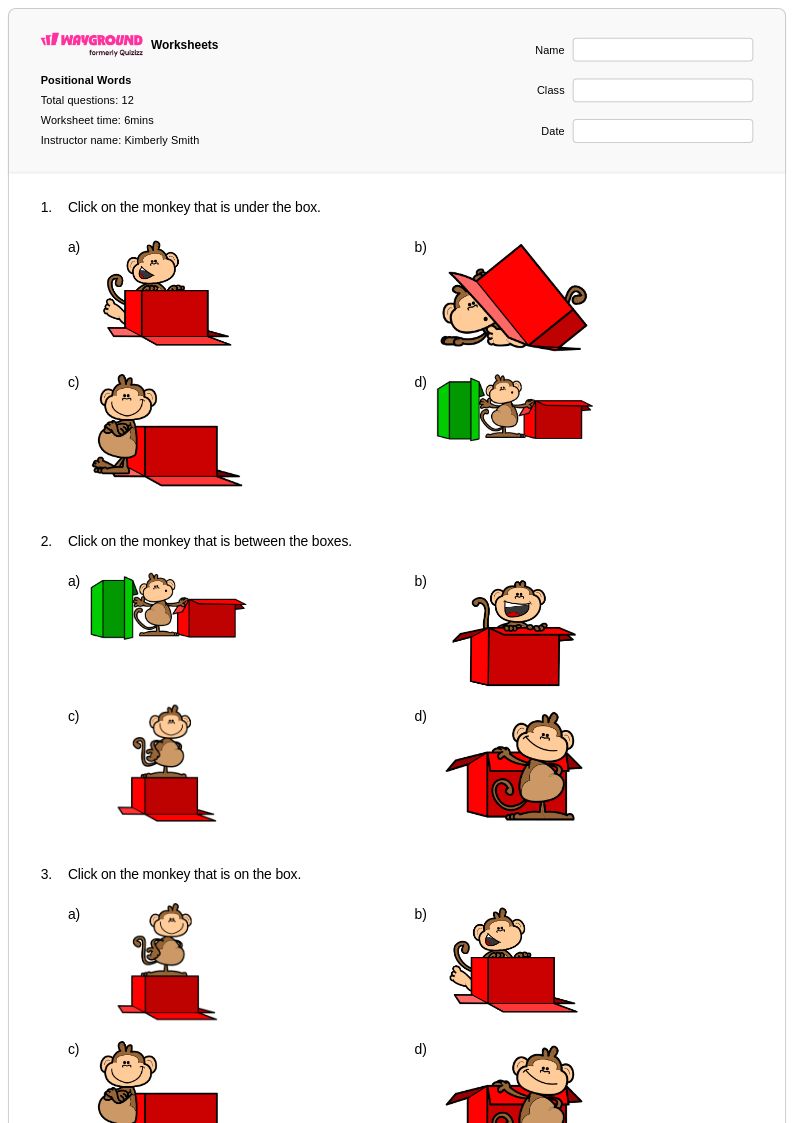
12 Hỏi
KG

20 Hỏi
9th - Uni

15 Hỏi
5th
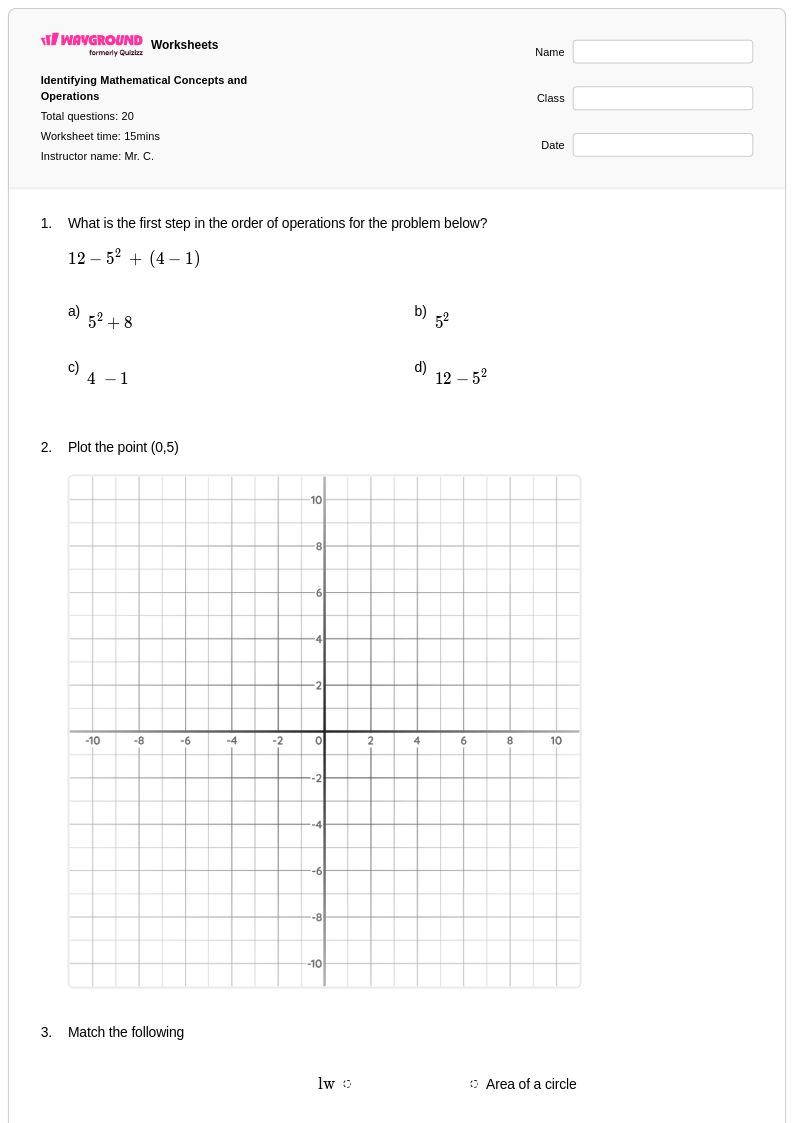
20 Hỏi
6th
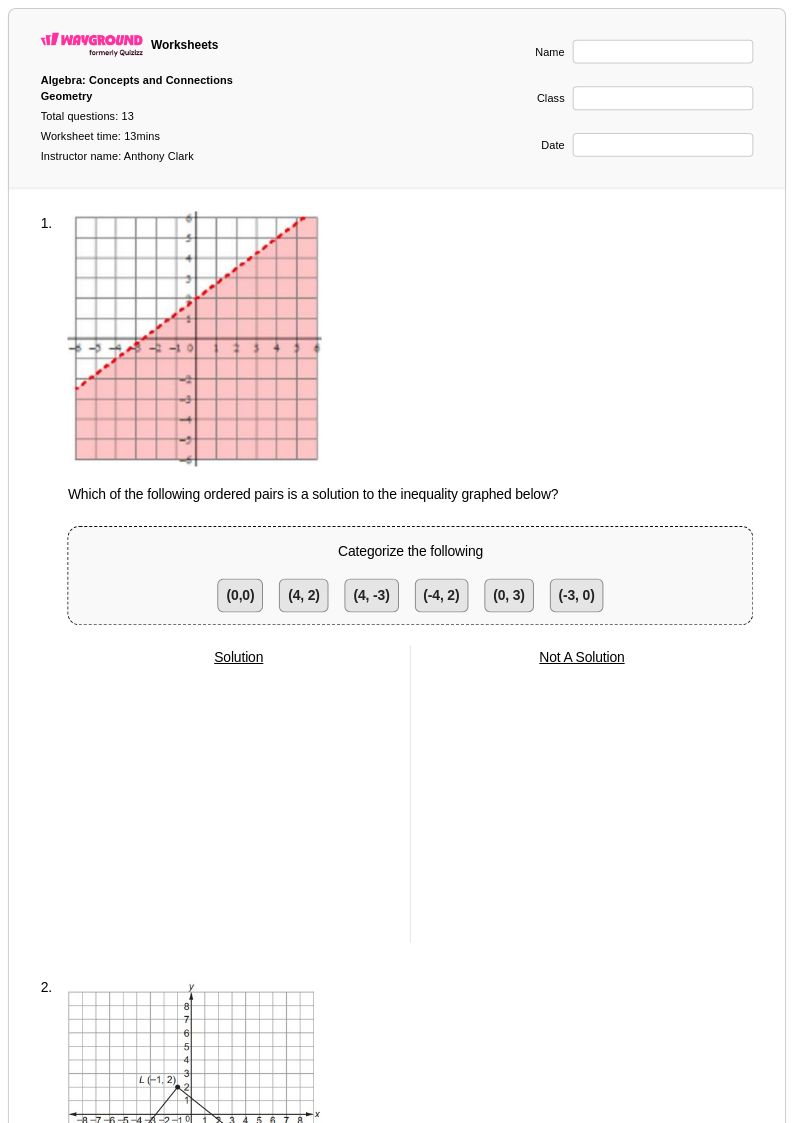
13 Hỏi
9th - Uni
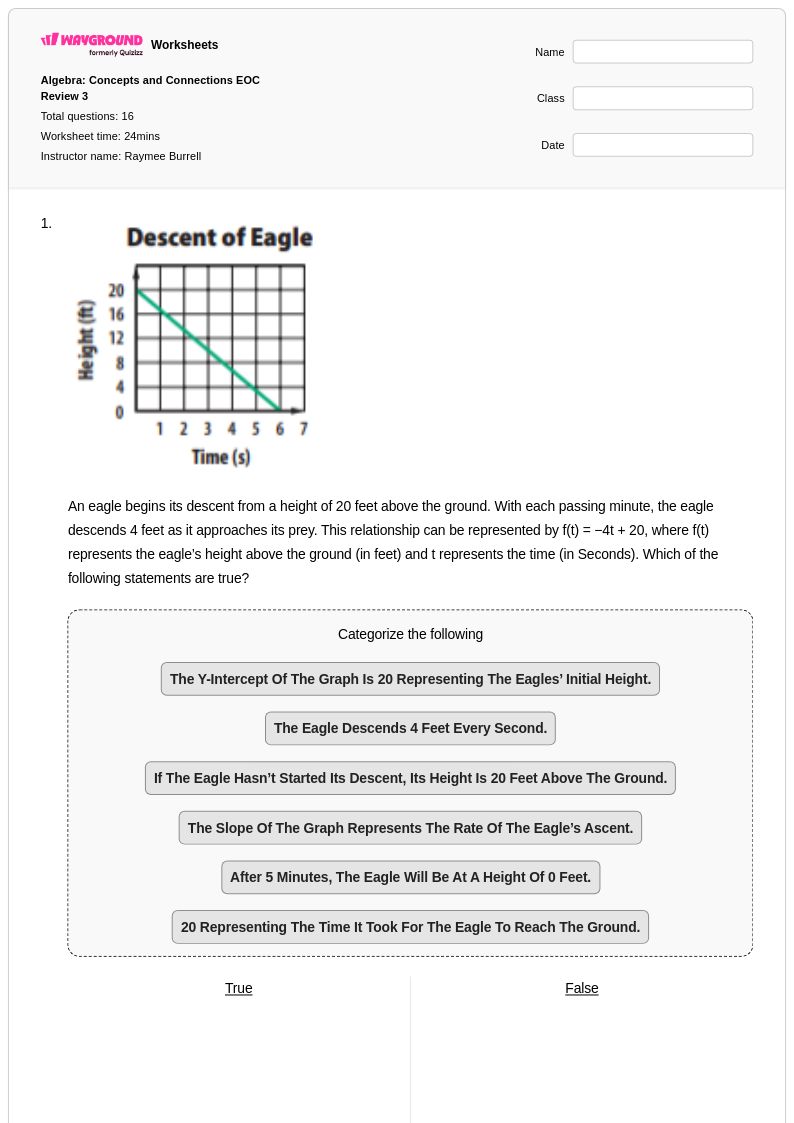
16 Hỏi
9th

12 Hỏi
7th

16 Hỏi
9th

9 Hỏi
4th
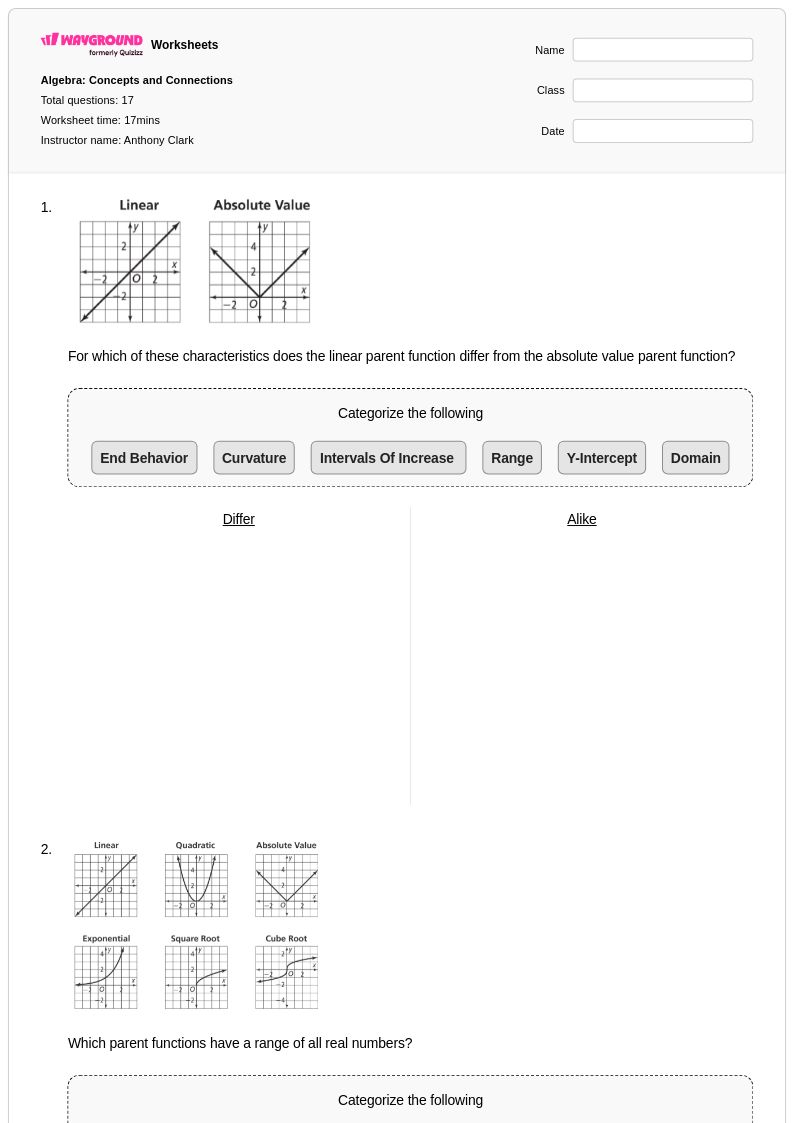
17 Hỏi
9th - Uni
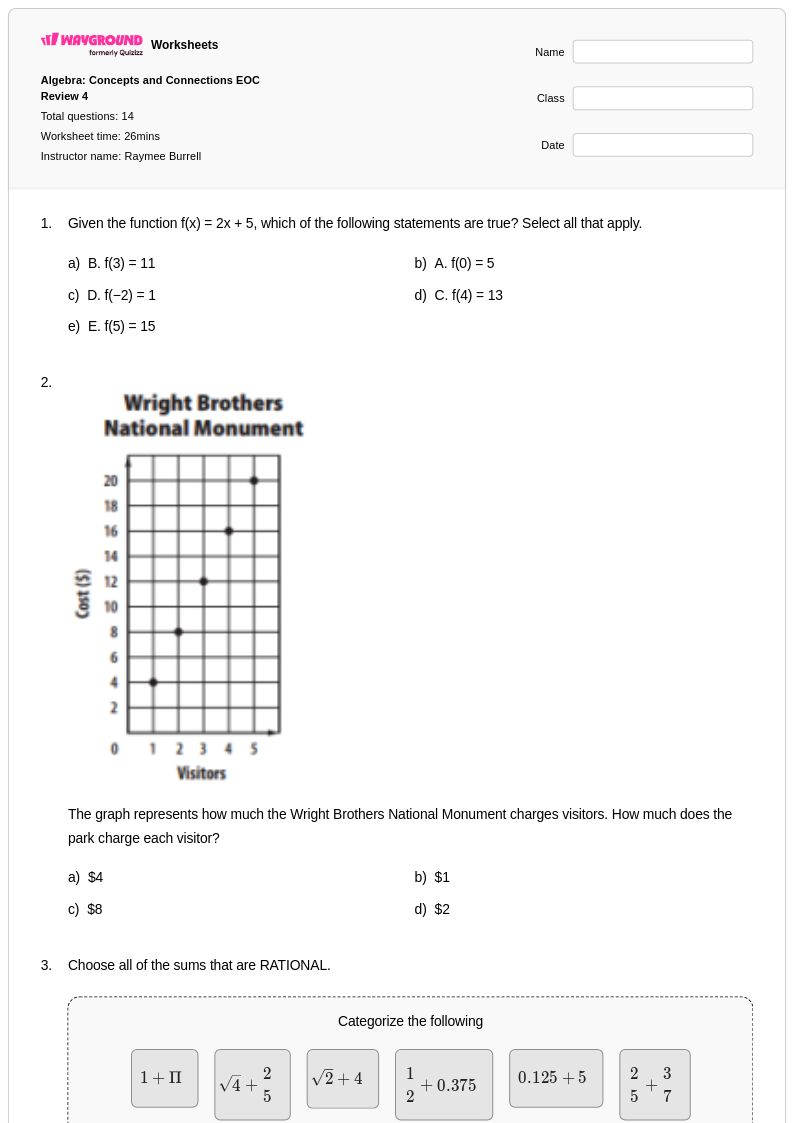
17 Hỏi
9th
15 Hỏi
9th - Uni
Tìm hiểu bài tập theo lớp
Khám phá bảng tính theo chủ đề
สำรวจแผ่นงาน แนวคิดเชิงพื้นที่ ที่พิมพ์ได้
แบบฝึกหัดเกี่ยวกับแนวคิดเชิงพื้นที่จาก Wayground (เดิมคือ Quizizz) มอบโอกาสในการฝึกฝนอย่างครอบคลุมสำหรับนักเรียน เพื่อพัฒนาทักษะการคิดเชิงสามมิติและการให้เหตุผลเชิงพื้นที่ ซึ่งเป็นพื้นฐานสำคัญของความเข้าใจทางเรขาคณิต แบบฝึกหัดคณิตศาสตร์เหล่านี้จะแนะนำผู้เรียนอย่างเป็นระบบเกี่ยวกับความสัมพันธ์เชิงพื้นที่ที่สำคัญ รวมถึงตำแหน่ง ทิศทาง การวางแนว และการเปลี่ยนแปลงของวัตถุในอวกาศ นักเรียนจะได้ฝึกฝนด้วยโจทย์ปัญหาที่จะเสริมสร้างความสามารถในการมองเห็นรูปทรงเรขาคณิตจากหลายมุมมอง เข้าใจระบบพิกัด และวิเคราะห์รูปแบบเชิงพื้นที่ แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียด และมีให้ดาวน์โหลดเป็นไฟล์ PDF ฟรี ช่วยให้ครูผู้สอนสามารถบูรณาการการสอนแนวคิดเชิงพื้นที่เข้ากับหลักสูตรคณิตศาสตร์ได้อย่างราบรื่น พร้อมทั้งมอบโอกาสที่เป็นระบบแก่นักเรียนในการฝึกฝนทักษะทางเรขาคณิตพื้นฐานเหล่านี้
Wayground (เดิมคือ Quizizz) ช่วยเสริมศักยภาพครูผู้สอนด้วยแบบฝึกหัดเกี่ยวกับแนวคิดเชิงพื้นที่ที่สร้างโดยครูหลายล้านชุด ซึ่งสนับสนุนการสอนคณิตศาสตร์อย่างครอบคลุมในสภาพแวดล้อมการเรียนรู้ที่หลากหลาย แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่มีประสิทธิภาพ ช่วยให้ครูสามารถค้นหาแหล่งข้อมูลที่สอดคล้องกับมาตรฐานและวัตถุประสงค์การเรียนรู้ที่เฉพาะเจาะจงได้อย่างรวดเร็ว ในขณะที่เครื่องมือการปรับให้เหมาะสมกับระดับทักษะและความต้องการการเรียนรู้ที่หลากหลาย ช่วยให้สามารถปรับแต่งได้ตามระดับความสามารถ ชุดแบบฝึกหัดเหล่านี้มีให้เลือกทั้งในรูปแบบไฟล์ PDF ที่พิมพ์ได้และรูปแบบดิจิทัล ซึ่งให้ความยืดหยุ่นสำหรับการสอนในห้องเรียน การบ้าน และการฝึกฝนด้วยตนเอง ครูสามารถวางแผนกิจกรรมการแก้ไขปัญหาสำหรับนักเรียนที่ประสบปัญหาเกี่ยวกับการมองเห็นเชิงพื้นที่ ออกแบบโอกาสในการเสริมสร้างความรู้สำหรับผู้เรียนที่มีความสามารถสูง และสร้างแบบฝึกหัดทักษะเฉพาะด้านที่เสริมสร้างแนวคิดทางเรขาคณิตผ่านแบบฝึกหัดที่เป็นระบบและมีลำดับขั้นตอน ซึ่งจะช่วยสร้างความสามารถในการให้เหตุผลเชิงพื้นที่ได้เมื่อเวลาผ่านไป
