
15 P
4th

15 P
4th
8 P
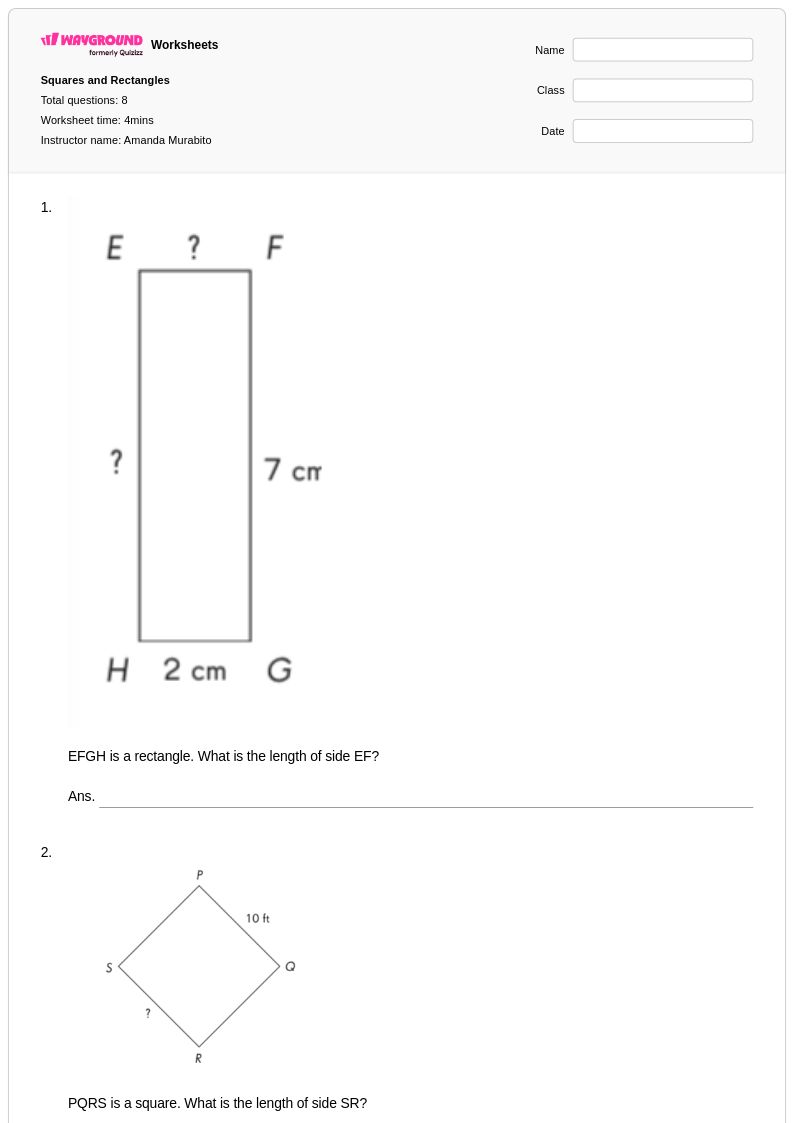
4th
15 P
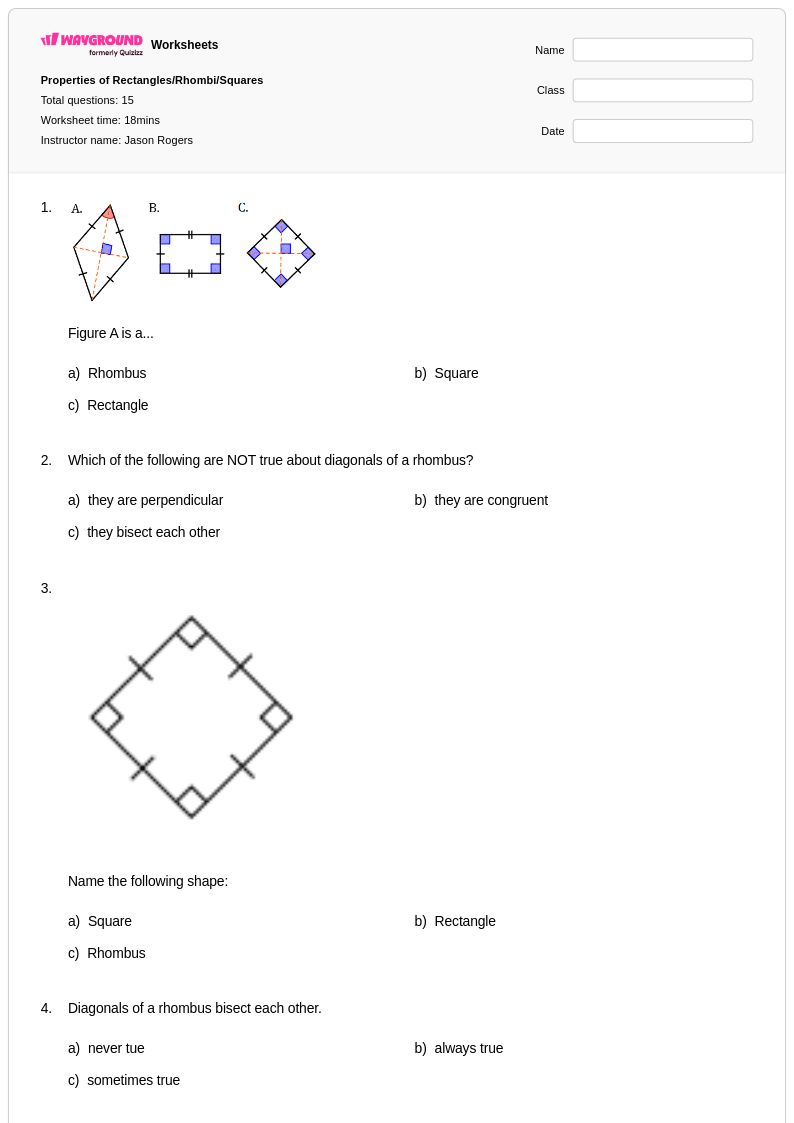
10th

14 P
4th

21 P
8th - 10th

6 P
9th
20 P
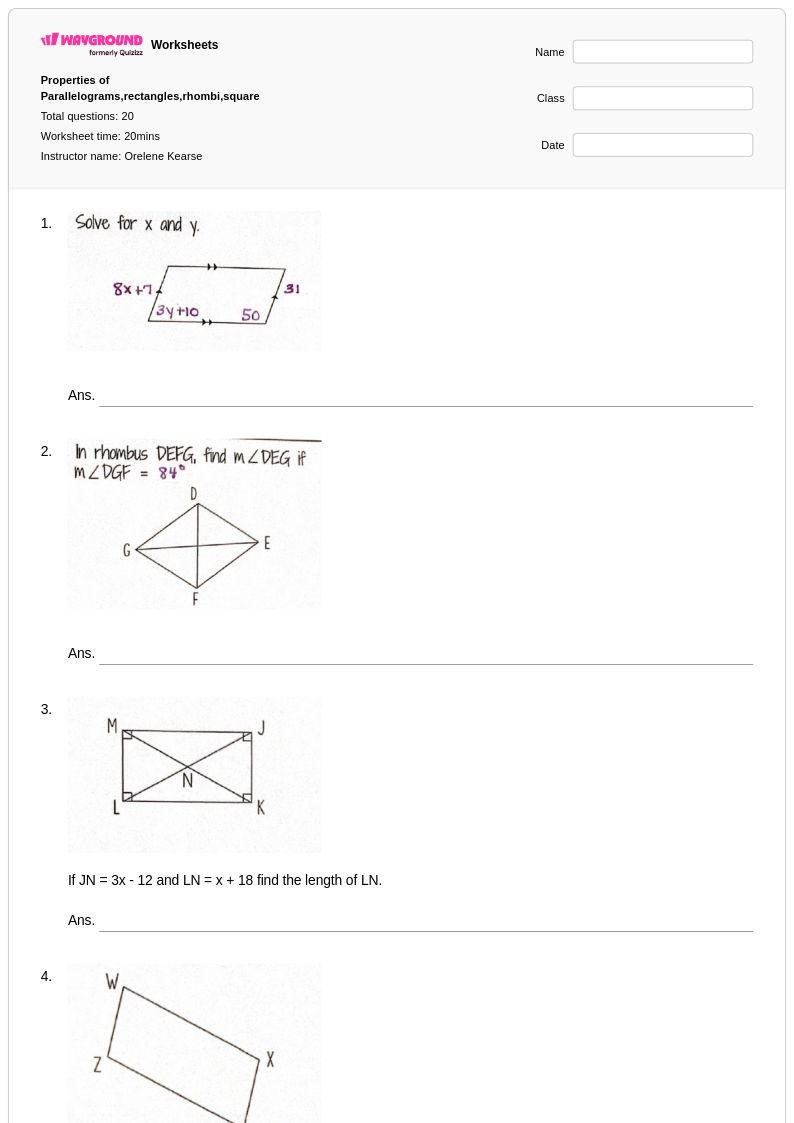
10th
20 P
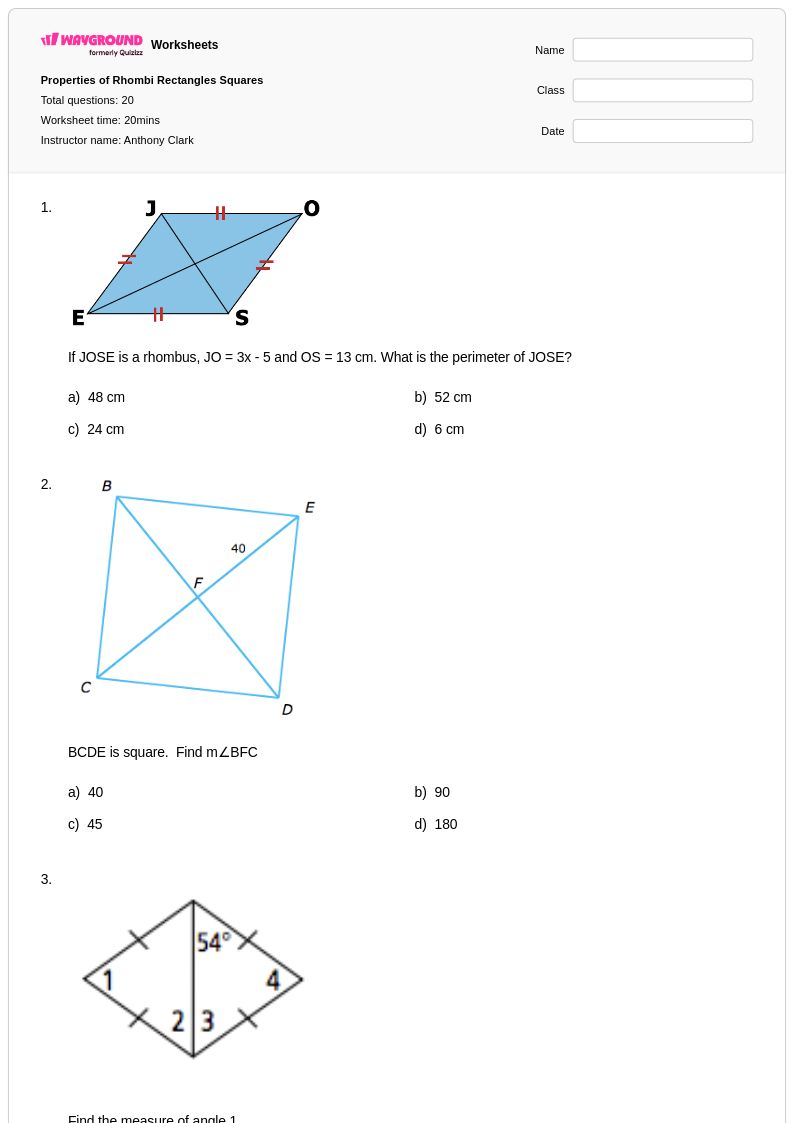
10th - Uni

10 P
10th

15 P
3rd - 5th

23 P
10th
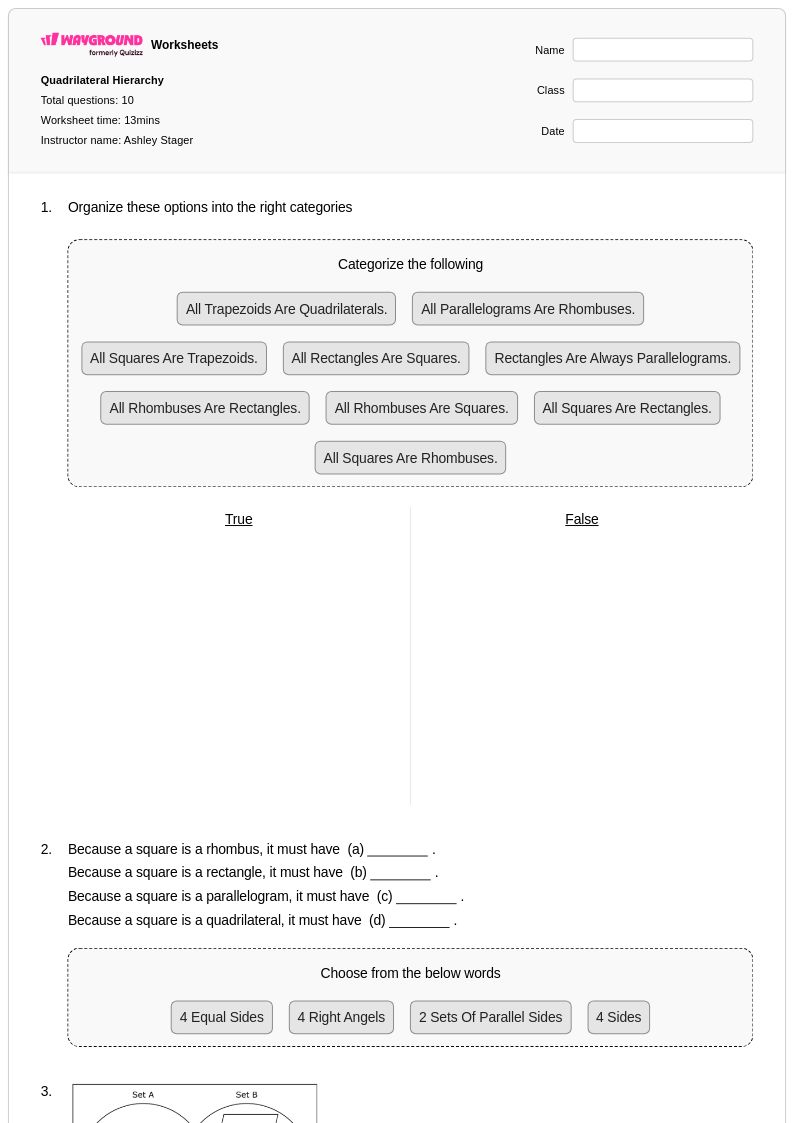
10 P
5th

20 P
5th - Uni

20 P
6th - 8th

11 P
6th
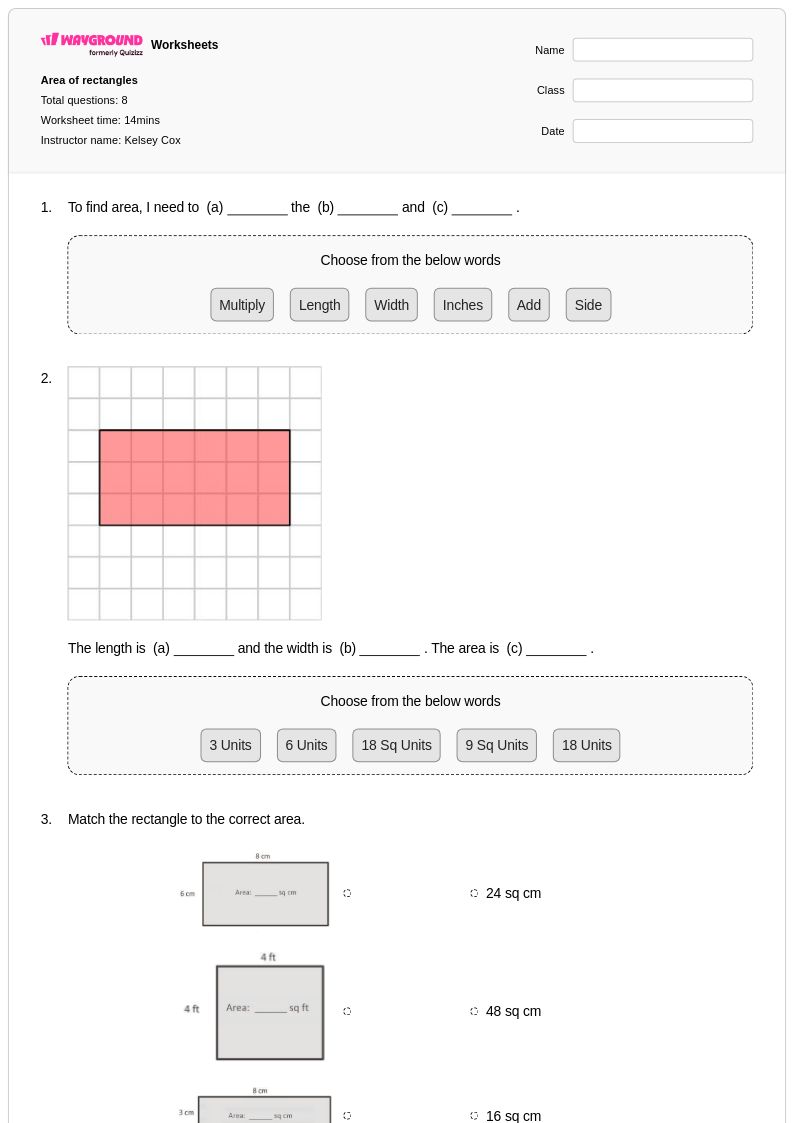
8 P
3rd

13 P
4th - 6th
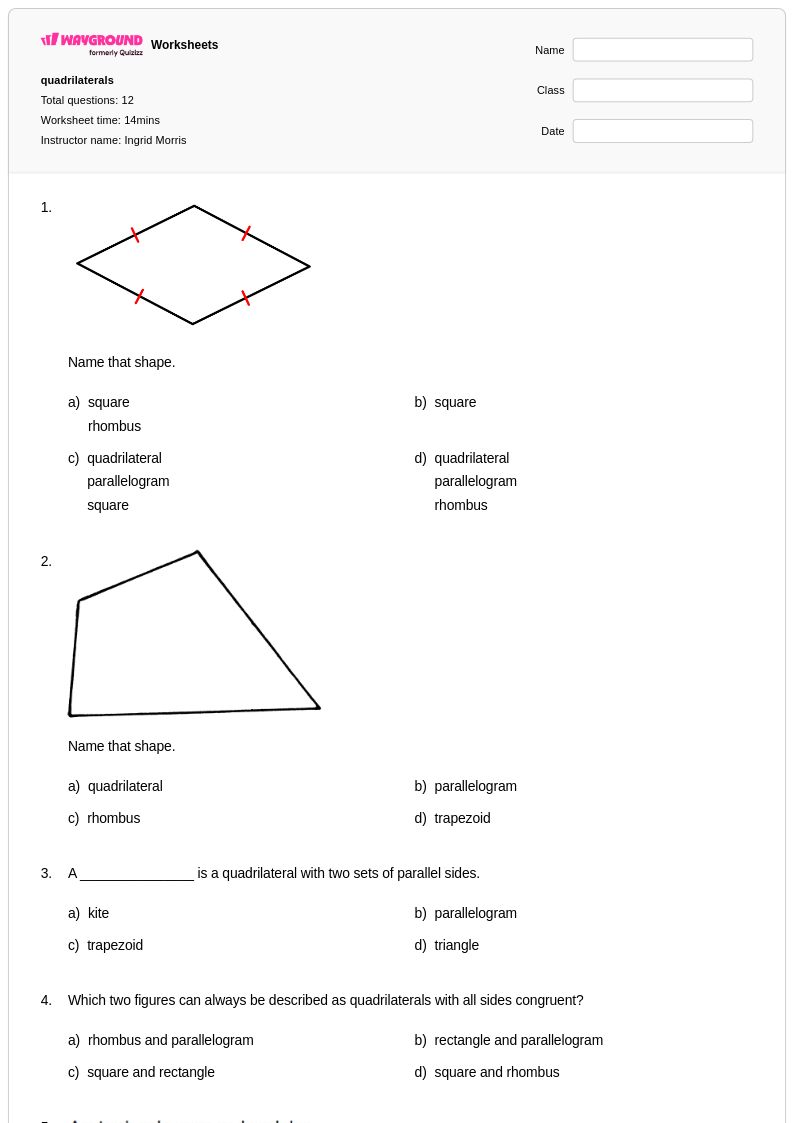
12 P
9th - 12th

17 P
5th - Uni
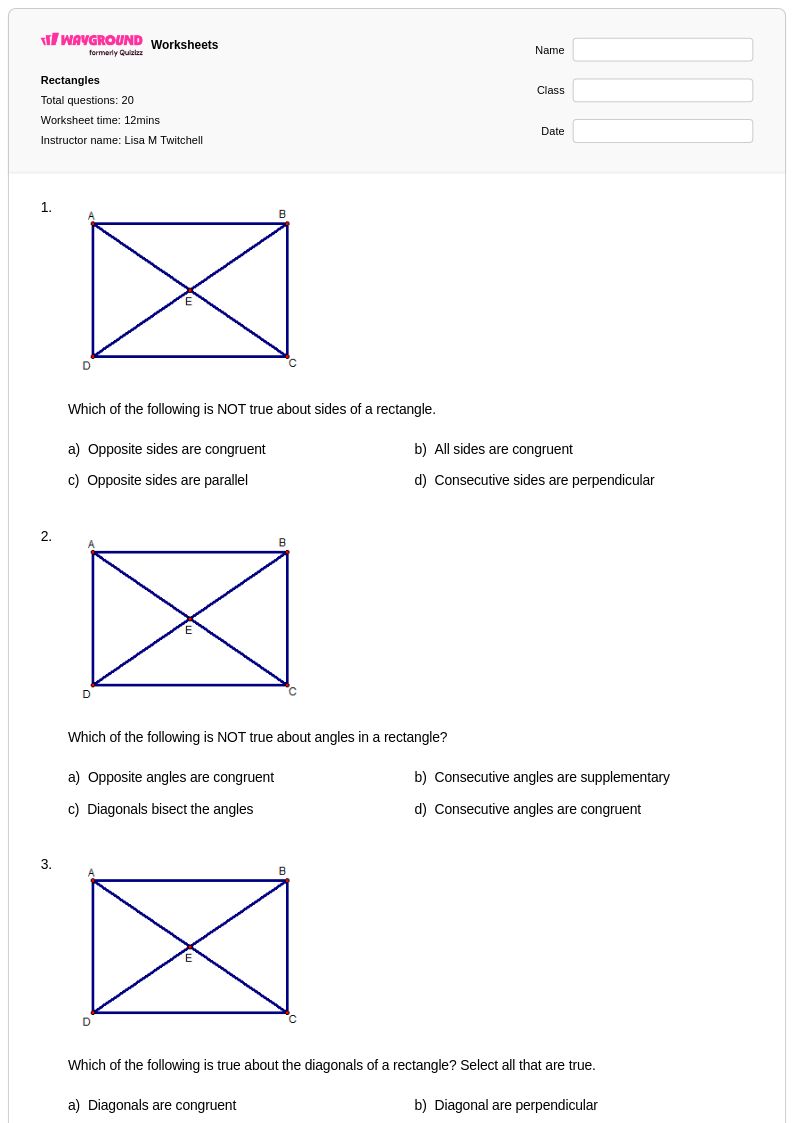
20 P
9th - 10th

18 P
10th

17 P
9th - 12th

20 P
5th - Uni
Przeglądaj arkusze według tematów
สำรวจแผ่นงาน คุณสมบัติของรูปสี่เหลี่ยมจัตุรัสและสี่เหลี่ยมผืนผ้า ที่พิมพ์ได้
แบบฝึกหัดเรื่องคุณสมบัติของรูปสี่เหลี่ยมจัตุรัสและสี่เหลี่ยมผืนผ้าจาก Wayground (เดิมคือ Quizizz) ครอบคลุมเนื้อหาพื้นฐานที่สำคัญของรูปสี่เหลี่ยมเหล่านี้ในวิชาเรขาคณิตอย่างครบถ้วน แบบฝึกหัดเหล่านี้จัดทำขึ้นอย่างเชี่ยวชาญ ช่วยให้นักเรียนเข้าใจแนวคิดสำคัญๆ เช่น ความสัมพันธ์ของด้าน การวัดมุม คุณสมบัติของเส้นทแยงมุม การคำนวณเส้นรอบวงและพื้นที่ และความสัมพันธ์เชิงลำดับชั้นระหว่างสี่เหลี่ยมผืนผ้าและสี่เหลี่ยมจัตุรัส แบบฝึกหัดเหล่านี้ช่วยเสริมสร้างทักษะการคิดวิเคราะห์ โดยนักเรียนจะได้สำรวจว่าสี่เหลี่ยมจัตุรัสเป็นกรณีพิเศษของสี่เหลี่ยมผืนผ้าอย่างไร ศึกษาคุณสมบัติเฉพาะของมุมฉากและด้านขนาน และนำสูตรทางเรขาคณิตไปใช้ในการแก้ปัญหา ครูสามารถเข้าถึงเฉลยคำตอบได้ครบถ้วนพร้อมกับแบบฝึกหัดแต่ละชุด โดยมีไฟล์ PDF ให้ดาวน์โหลดฟรี ทำให้ง่ายต่อการนำแบบฝึกหัดที่ต้องการไปใช้ในการเรียนการสอนหรือการบ้าน
Wayground (เดิมคือ Quizizz) ช่วยให้ครูผู้สอนมีคลังแบบฝึกหัดที่สร้างโดยครูหลายล้านชุด โดยเน้นที่คุณสมบัติของสี่เหลี่ยมจัตุรัสและสี่เหลี่ยมผืนผ้า พร้อมด้วยระบบค้นหาและกรองข้อมูลที่มีประสิทธิภาพ ช่วยให้การวางแผนบทเรียนง่ายขึ้น คุณสมบัติการจัดเรียงตามมาตรฐานของแพลตฟอร์มช่วยให้มั่นใจได้ว่าแบบฝึกหัดที่เลือกตรงตามข้อกำหนดของหลักสูตรเฉพาะ ในขณะที่เครื่องมือการปรับระดับความยากง่ายในตัวช่วยให้ครูสามารถปรับระดับความยากและความซับซ้อนของเนื้อหาให้ตรงกับความต้องการที่หลากหลายของนักเรียน สื่อการเรียนรู้ที่หลากหลายเหล่านี้มีให้เลือกทั้งในรูปแบบสิ่งพิมพ์และดิจิทัล รวมถึงเวอร์ชัน PDF ที่ดาวน์โหลดได้ ซึ่งให้ความยืดหยุ่นสูงสุดสำหรับการนำไปใช้ในห้องเรียน การเรียนรู้ทางไกล หรือรูปแบบการเรียนการสอนแบบผสมผสาน ครูใช้ประโยชน์จากชุดแบบฝึกหัดที่ครอบคลุมเหล่านี้สำหรับการฝึกฝนทักษะเฉพาะด้าน การสนับสนุนการแก้ไขปัญหาสำหรับผู้เรียนที่ประสบปัญหา และโอกาสในการเสริมสร้างความรู้สำหรับนักเรียนที่มีความสามารถสูง สร้างเส้นทางที่เป็นระบบสำหรับการเรียนรู้แนวคิดทางเรขาคณิตซึ่งเป็นรากฐานสำหรับการให้เหตุผลทางคณิตศาสตร์ที่ซับซ้อนยิ่งขึ้น
