
20Q
7th - Uni
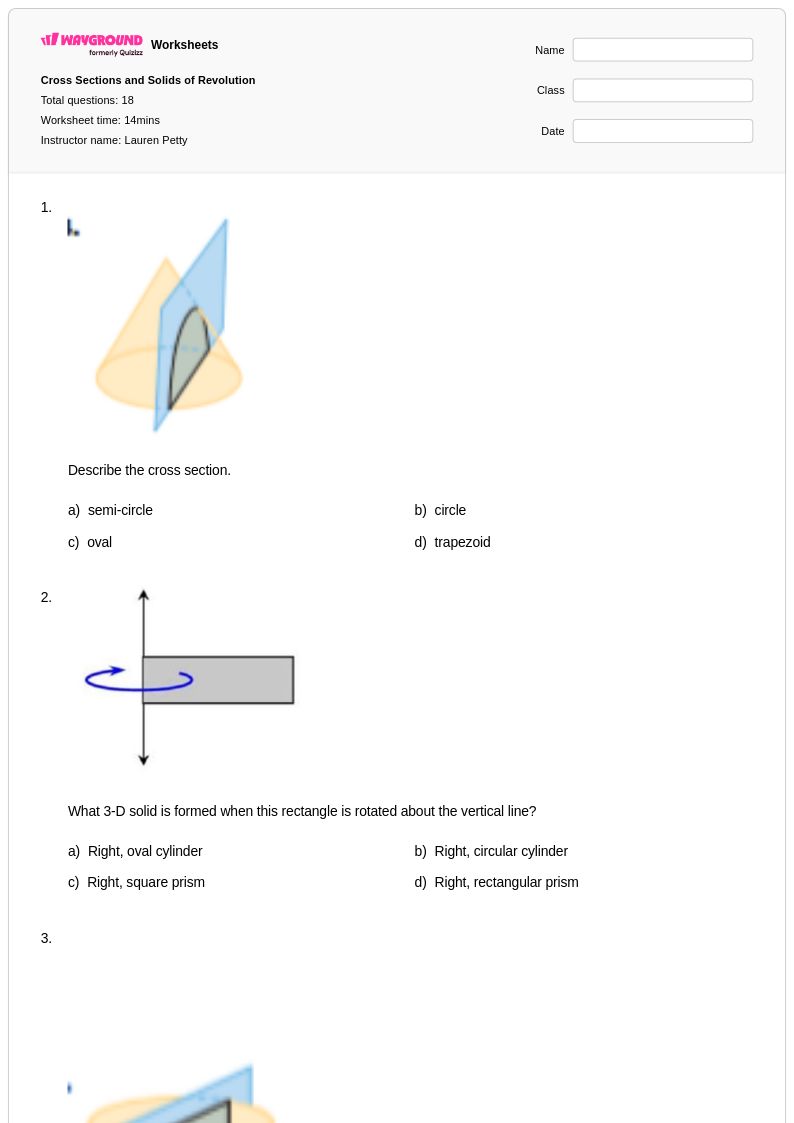
18Q
10th - 11th
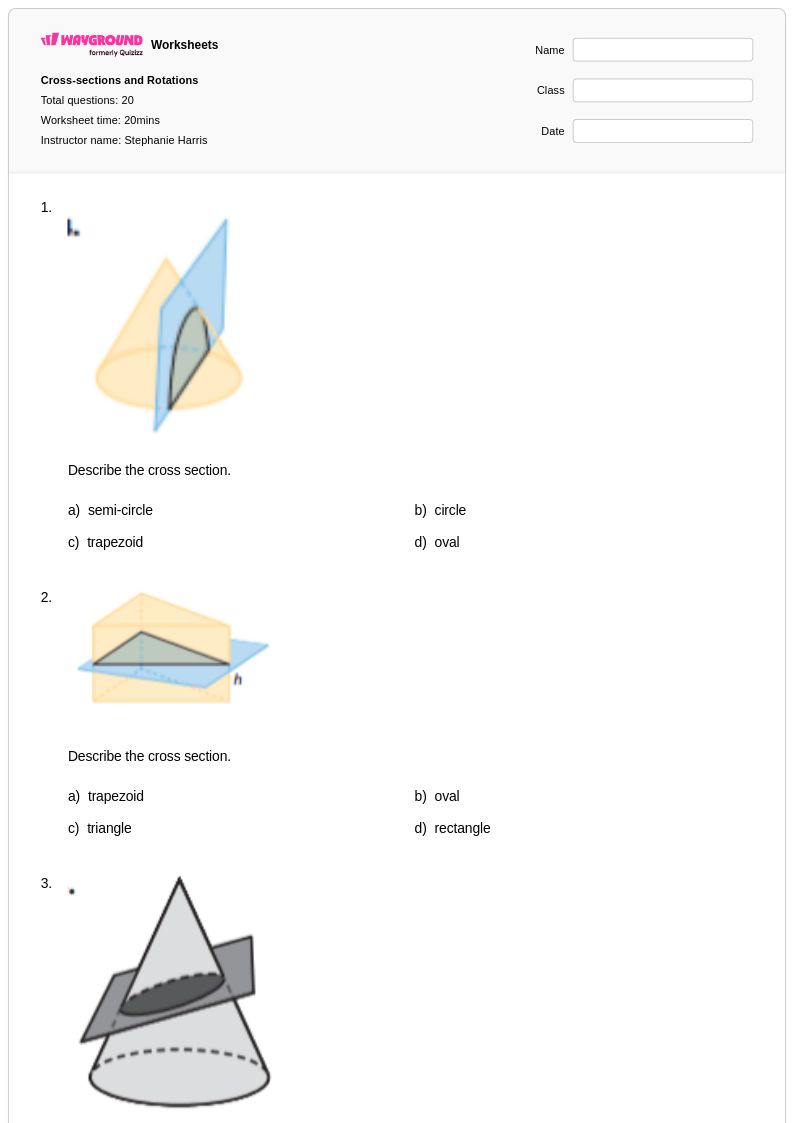
20Q
9th - 12th
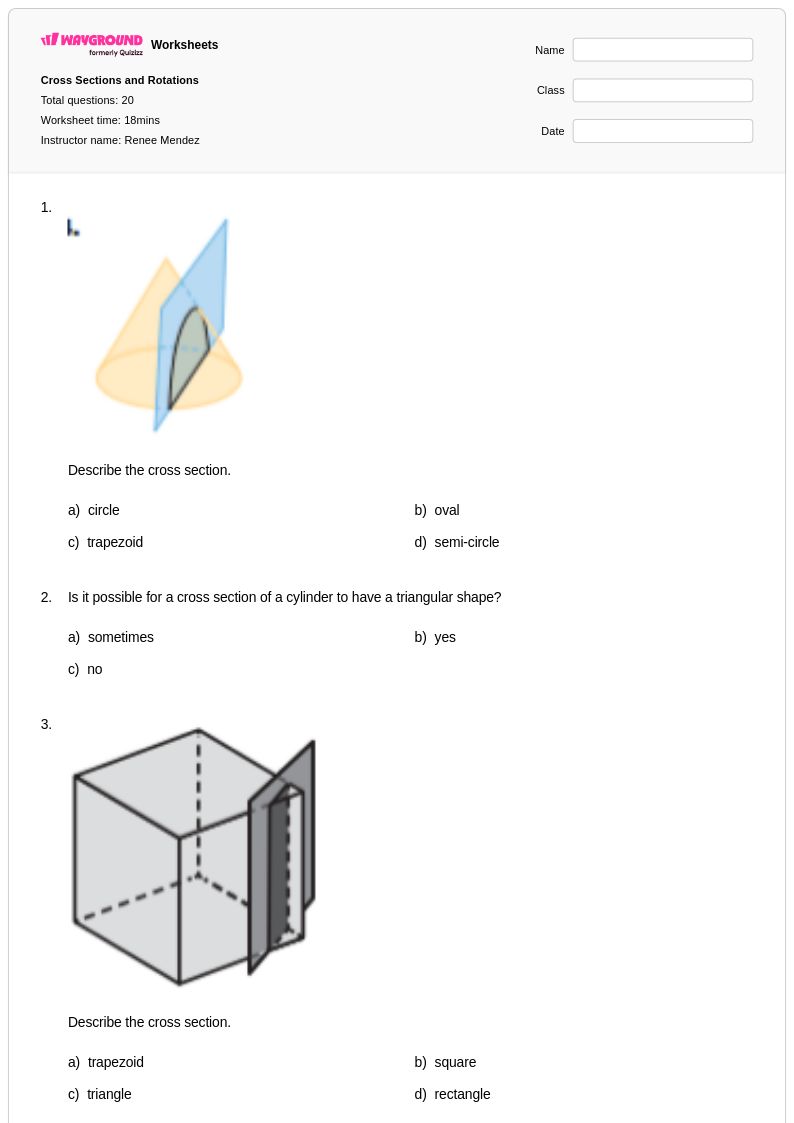
20Q
9th - 12th
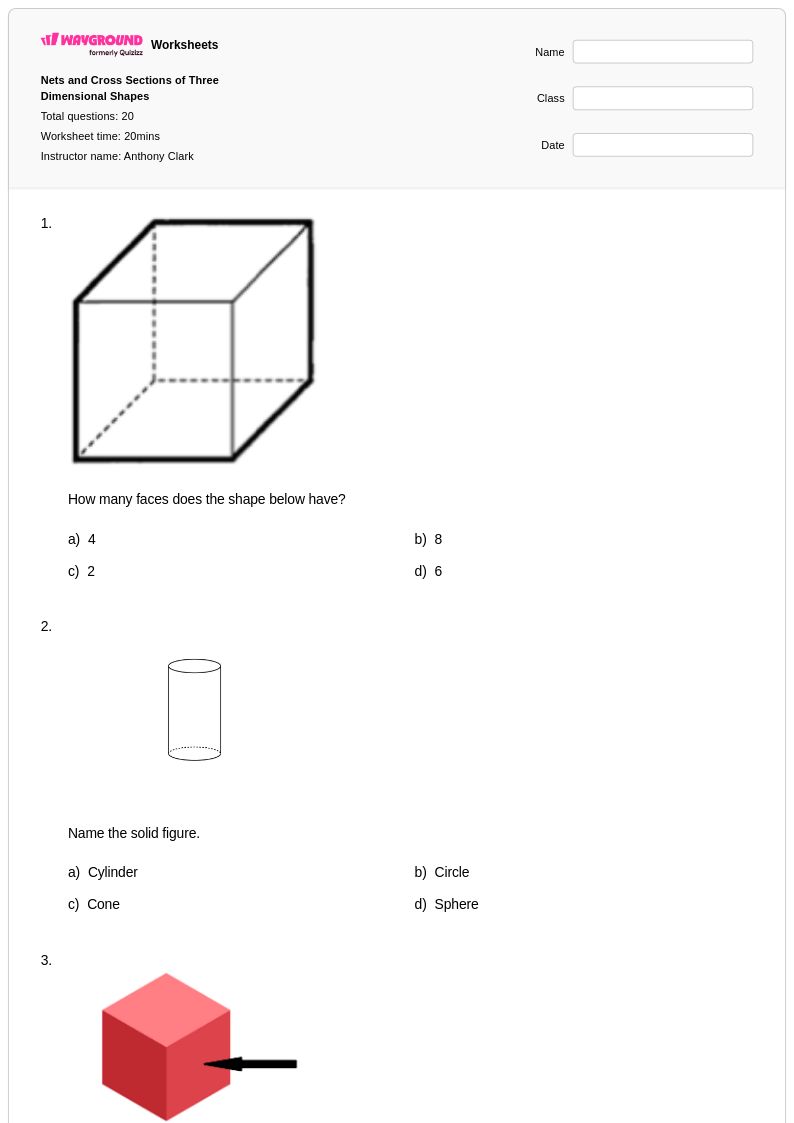
20Q
3rd - Uni
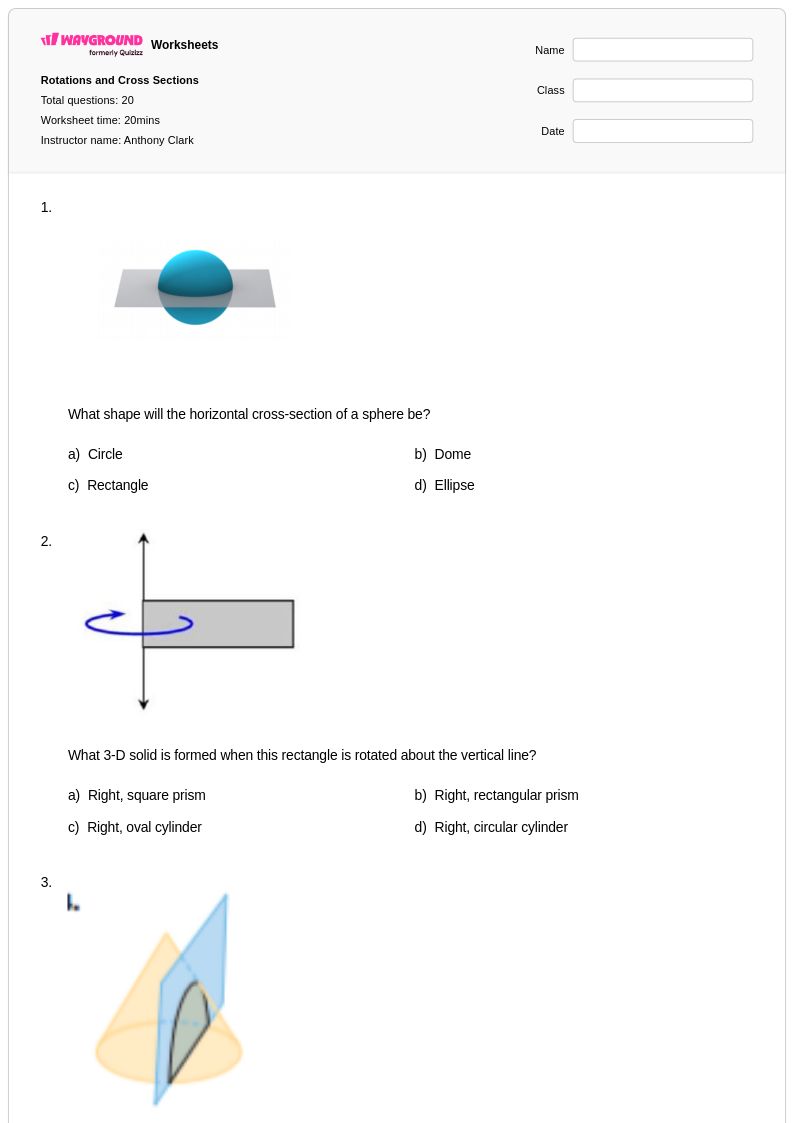
20Q
10th - Uni
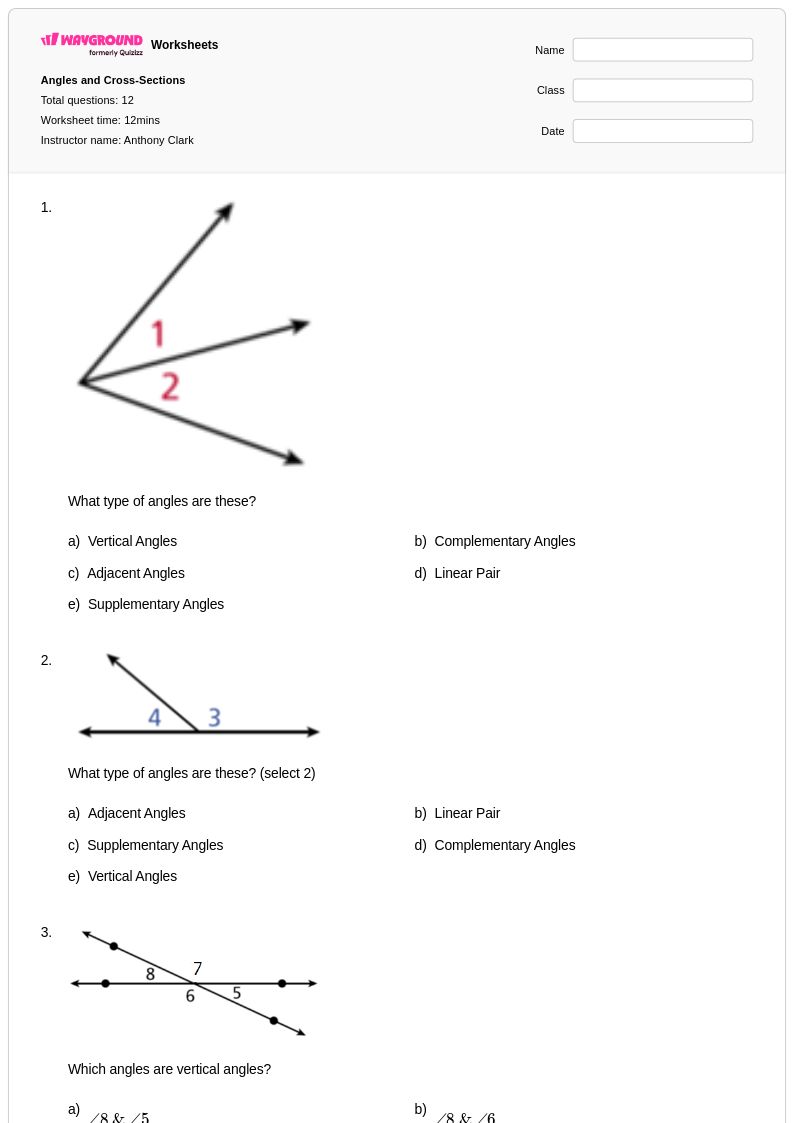
12Q
10th - Uni
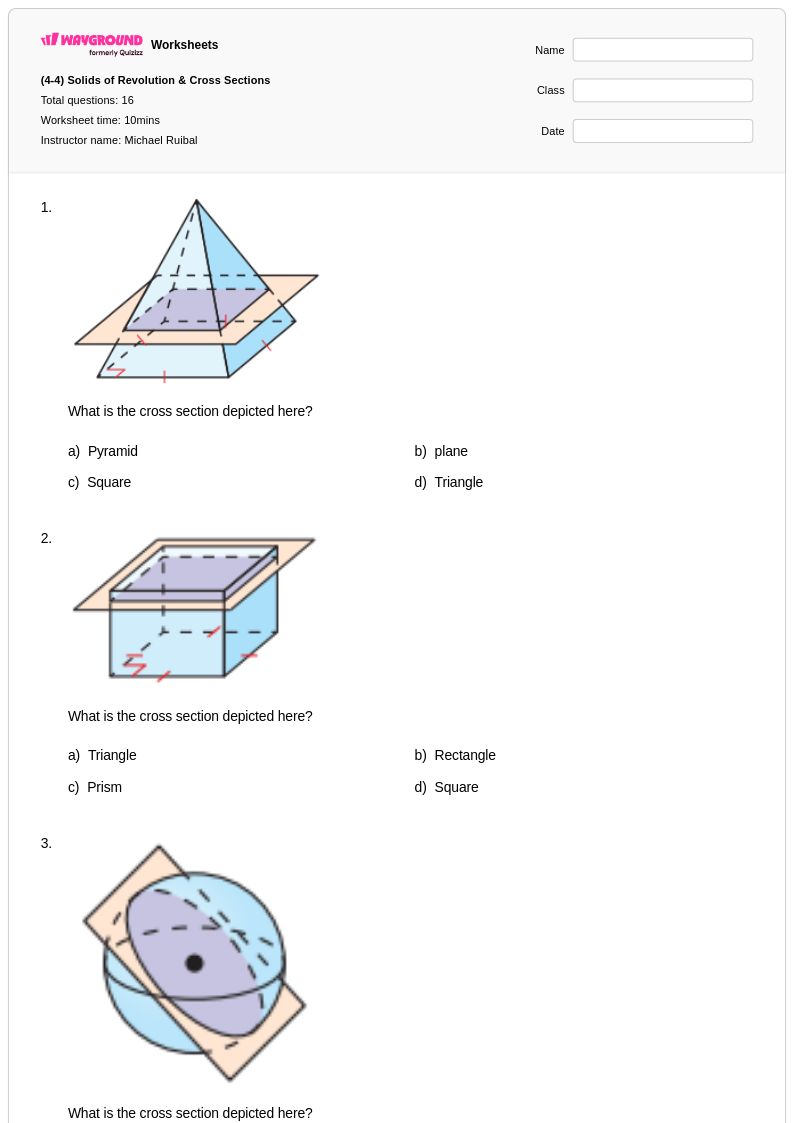
16Q
10th - 12th
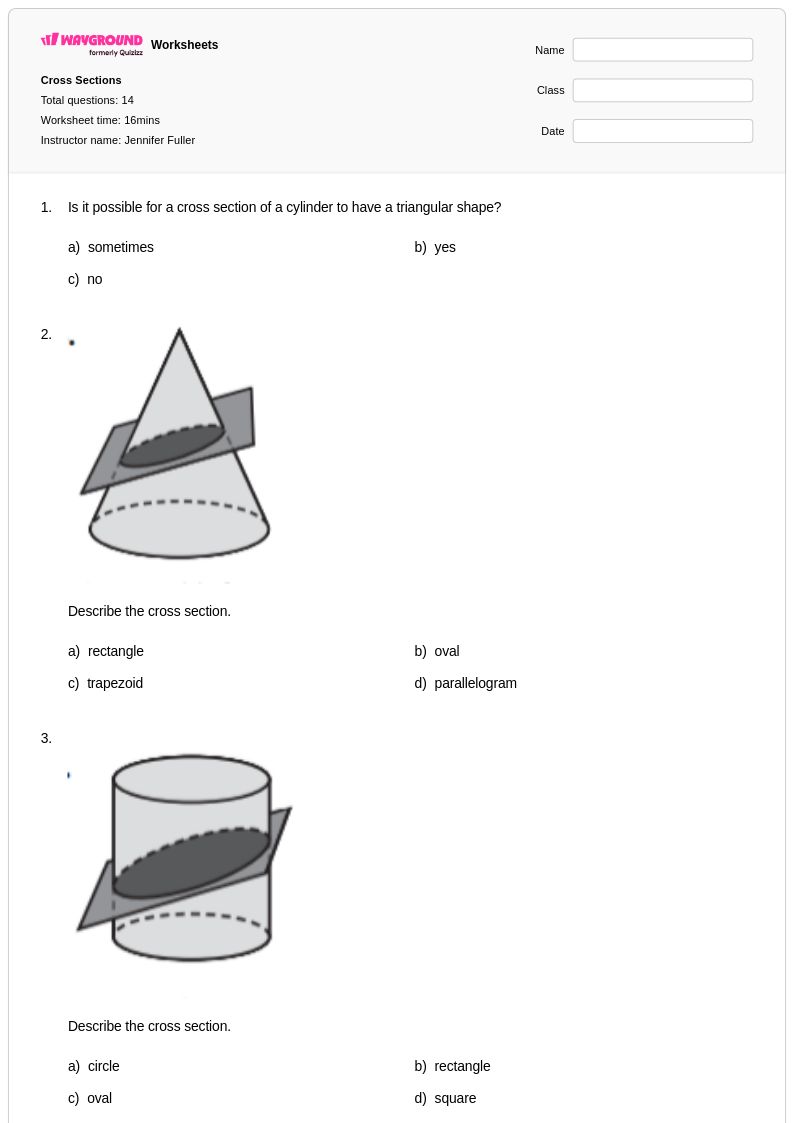
14Q
9th - 12th

20Q
10th - Uni

29Q
11th
20Q
10th - Uni
23Q
9th - 12th
20Q
10th - Uni

11Q
7th - Uni
15Q
10th - Uni
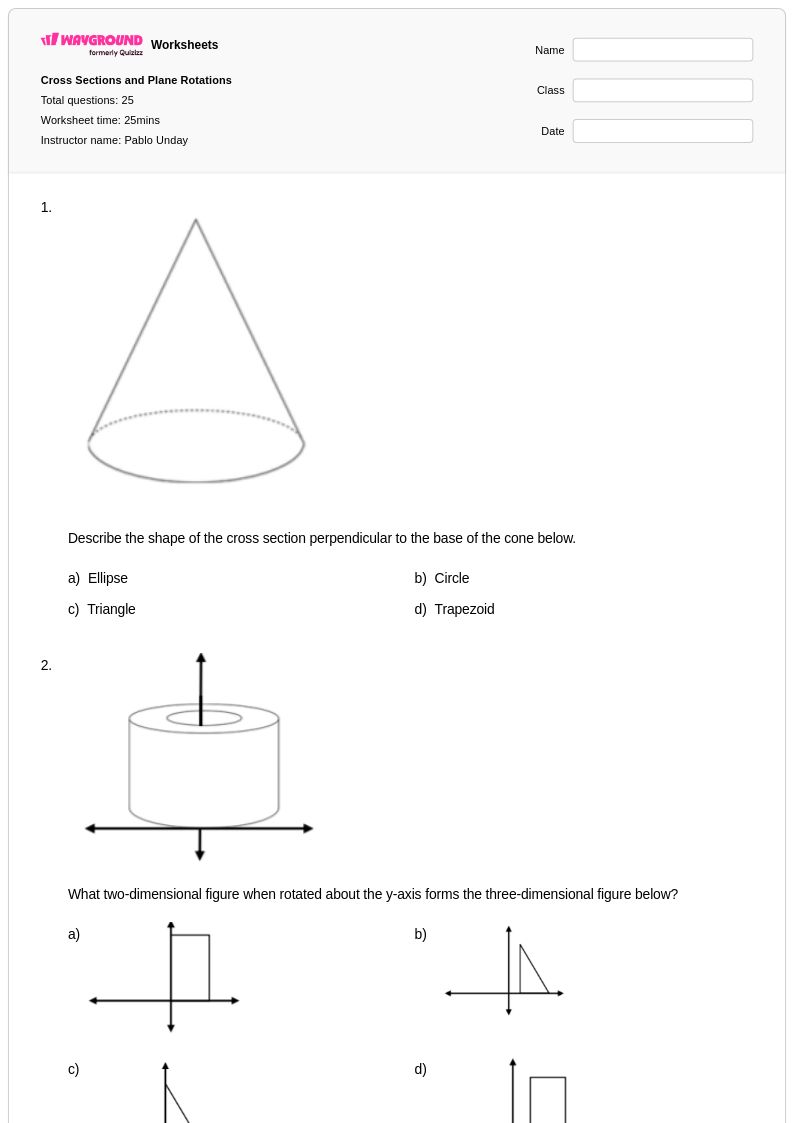
25Q
9th - 12th
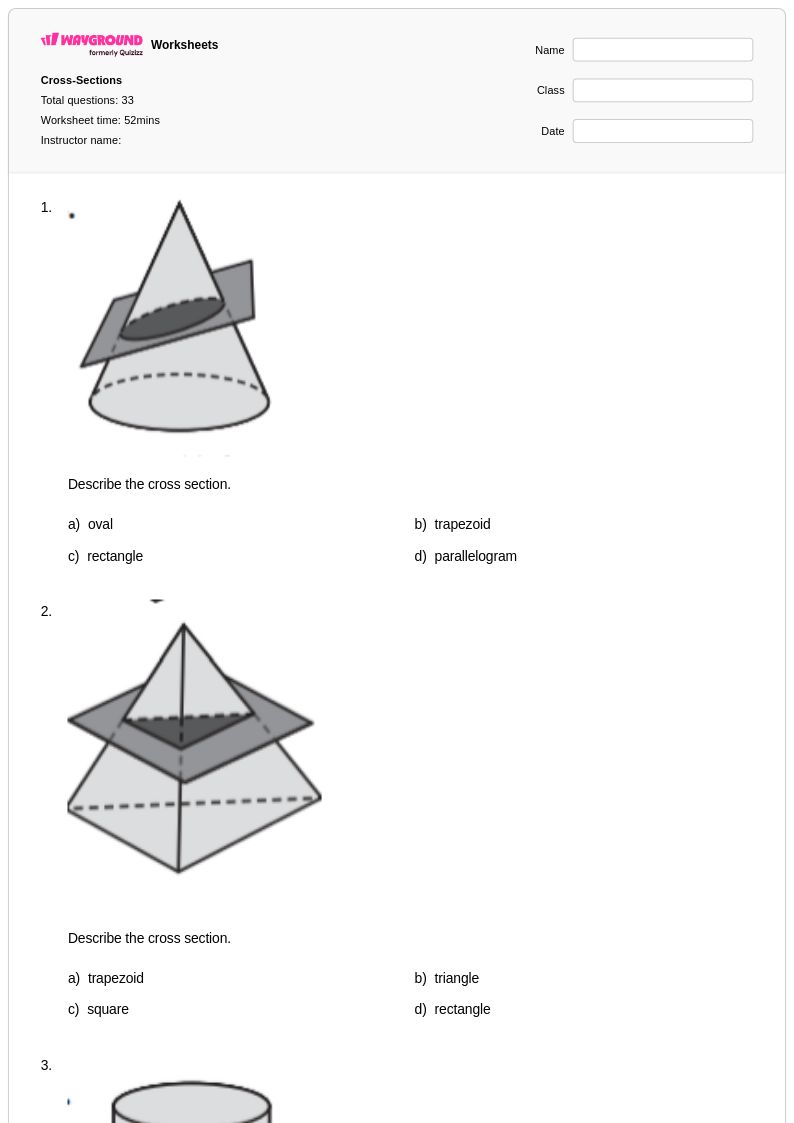
33Q
11th

15Q
7th - Uni
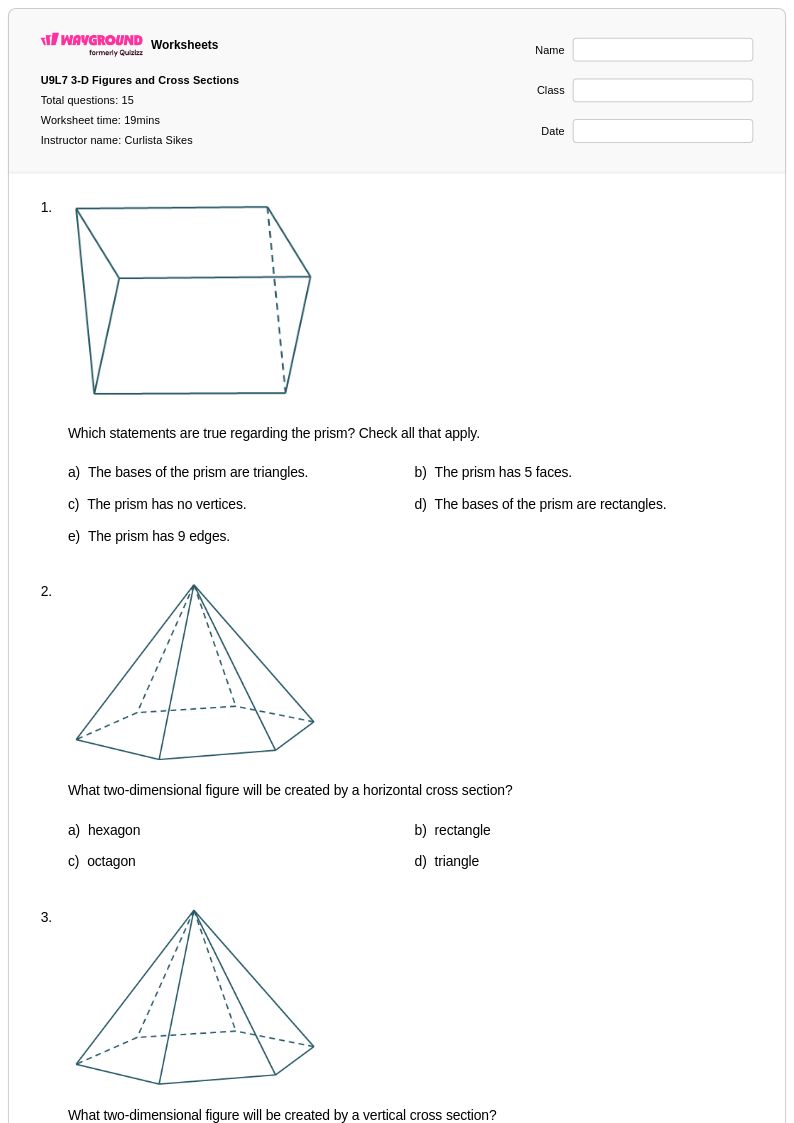
15Q
9th - 12th

56Q
9th - 12th

20Q
7th - Uni
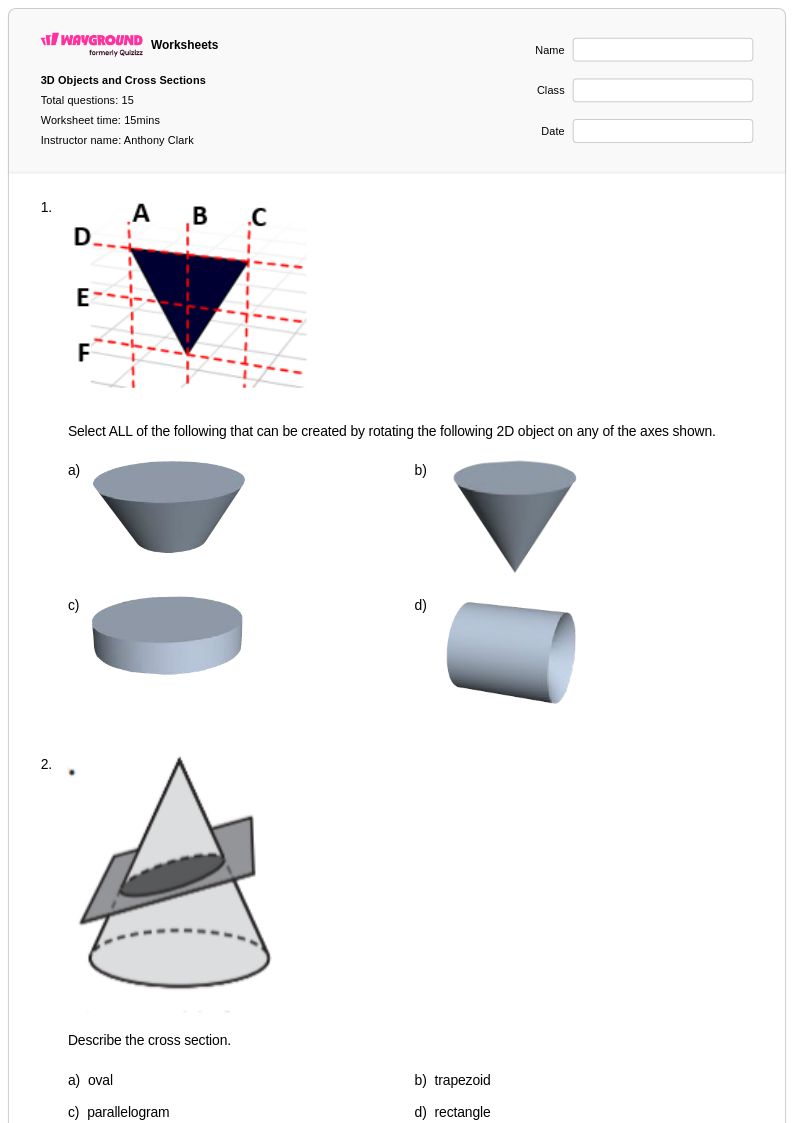
15Q
10th - Uni

10Q
10th - Uni
Explore otras hojas de trabajo de materias para ระดับ 11
สำรวจแผ่นงาน ภาคตัดขวาง ที่พิมพ์ได้สำหรับ ชั้นประถมศึกษาปีที่ 11
การตัดขวางในเรขาคณิตระดับชั้นมัธยมศึกษาปีที่ 4 (เกรด 11) เป็นแนวคิดสำคัญเกี่ยวกับการให้เหตุผลเชิงพื้นที่สามมิติ ซึ่งเชื่อมโยงความคิดเชิงพีชคณิตกับการมองเห็นภาพทางเรขาคณิตขั้นสูง แบบฝึกหัดการตัดขวางที่ครอบคลุมของ Wayground ช่วยให้นักเรียนได้ฝึกฝนอย่างเป็นระบบในการระบุ วาดภาพ และวิเคราะห์รูปทรงสองมิติที่เกิดขึ้นเมื่อระนาบตัดกับรูปทรงสามมิติ แบบฝึกหัดที่ออกแบบมาอย่างพิถีพิถันเหล่านี้ช่วยเสริมสร้างความสามารถของนักเรียนในการหมุนวัตถุในใจ ทำนายผลลัพธ์ทางเรขาคณิต และเข้าใจความสัมพันธ์ระหว่างรูปทรงสองมิติและสามมิติ แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียด และมีให้ดาวน์โหลดเป็นไฟล์ PDF ฟรี ช่วยให้นักเรียนสามารถฝึกฝนในสถานการณ์ที่ท้าทายมากขึ้นเรื่อยๆ เกี่ยวกับทรงกระบอก กรวย ปริซึม พีระมิด และทรงกลม เพื่อพัฒนาความเชี่ยวชาญในทักษะพื้นฐานนี้
คลังแบบฝึกหัดการตัดขวางที่สร้างโดยครูผู้สอนนับล้านชุดของ Wayground ช่วยให้ครูผู้สอนมีความยืดหยุ่นอย่างที่ไม่เคยมีมาก่อนในการจัดการเรียนการสอนเรขาคณิตที่แตกต่างกันสำหรับนักเรียนระดับชั้นมัธยมศึกษาปีที่ 4 (เกรด 11) แพลตฟอร์มนี้มีฟังก์ชันการค้นหาและการกรองที่มีประสิทธิภาพ ช่วยให้ครูสามารถค้นหาแหล่งข้อมูลที่สอดคล้องกับมาตรฐานหลักสูตรเฉพาะได้อย่างรวดเร็ว ในขณะที่เครื่องมือปรับแต่งในตัวช่วยให้สามารถปรับเปลี่ยนสื่อการเรียนรู้ได้อย่างราบรื่นเพื่อตอบสนองความต้องการการเรียนรู้ที่หลากหลาย ชุดแบบฝึกหัดเกี่ยวกับภาคตัดขวางเหล่านี้มีให้เลือกทั้งแบบพิมพ์และแบบดิจิทัล รวมถึงไฟล์ PDF ที่ดาวน์โหลดได้ ทำให้เหมาะสำหรับการเรียนการสอนในห้องเรียน การบ้าน การเรียนเสริม และกิจกรรมเสริม ครูสามารถวางแผนหน่วยการเรียนรู้เรขาคณิตแบบครบวงจรได้อย่างมีประสิทธิภาพโดยการเข้าถึงแบบฝึกหัดที่ค่อยๆ พัฒนาจากการระบุภาคตัดขวางขั้นพื้นฐานไปจนถึงสถานการณ์การแก้ปัญหาที่ซับซ้อน ทำให้มั่นใจได้ว่านักเรียนจะพัฒนาทั้งความคล่องแคล่วตามขั้นตอนและความเข้าใจเชิงแนวคิดเกี่ยวกับความสัมพันธ์ทางเรขาคณิตสามมิติ
