
7Q
Uni

20Q
8th
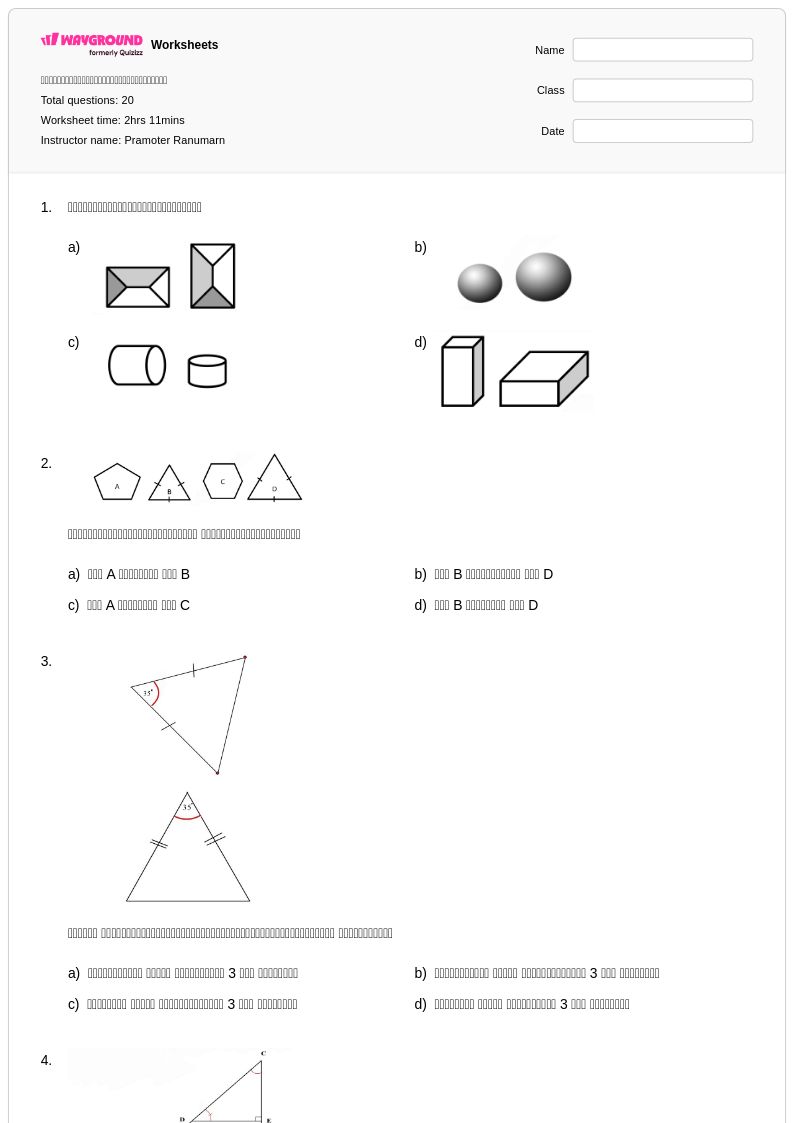
20Q
9th - 10th
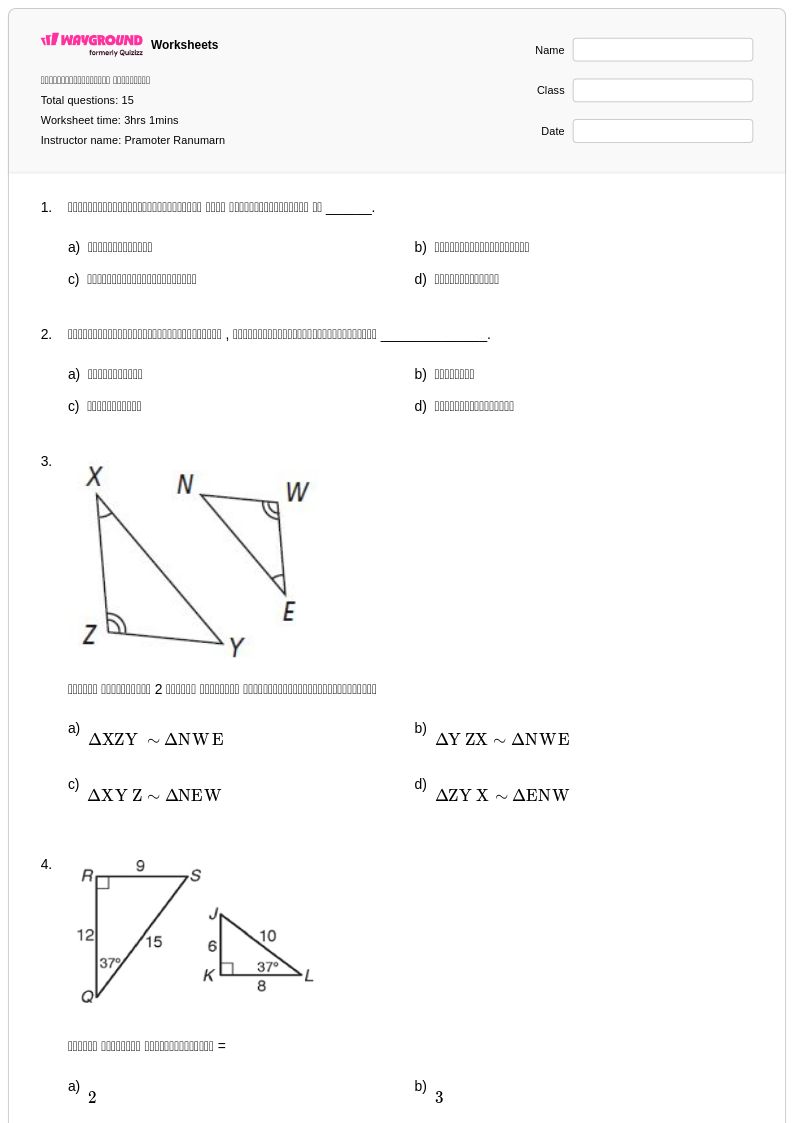
15Q
9th
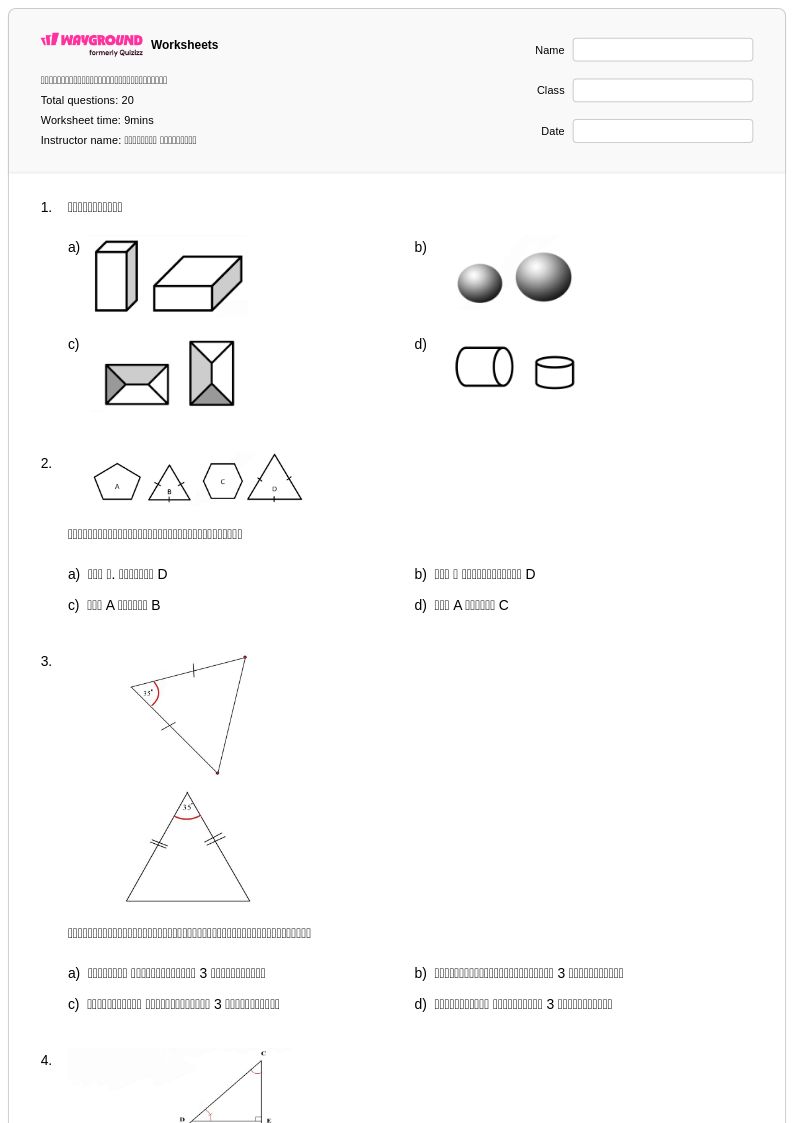
20Q
9th - 10th

10Q
9th

17Q
5th
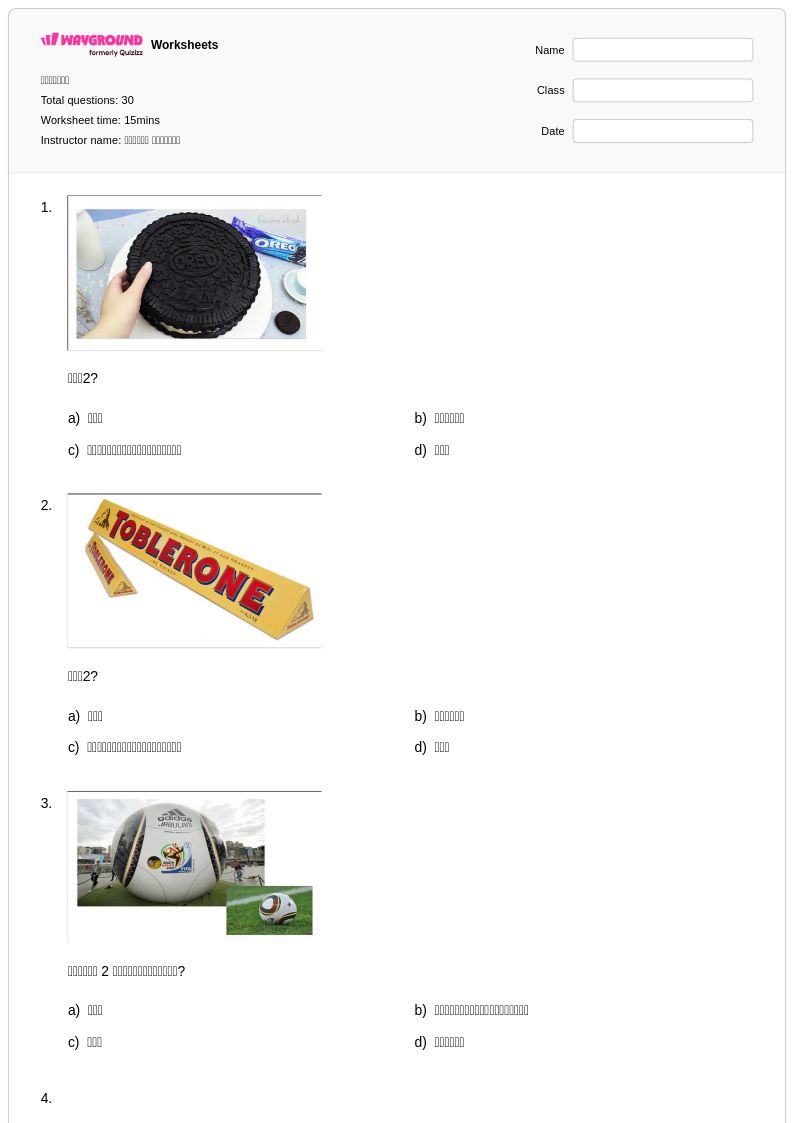
30Q
12th
20Q
9th - 12th
30Q
12th

20Q
8th
30Q
9th

15Q
Uni
20Q
9th - 12th

20Q
8th

20Q
8th

10Q
Uni

22Q
Uni

20Q
9th

20Q
9th

9Q
12th
18Q
8th

6Q
11th

30Q
1st
Explore planilhas por assuntos
สำรวจแผ่นงาน สามเหลี่ยมที่เท่ากันทุกประการ Sss Sas และ Asa ที่พิมพ์ได้
แบบฝึกหัดเรื่องสามเหลี่ยมที่เท่ากันทุกประการ (SSS, SAS และ ASA) ที่มีให้ดาวน์โหลดผ่าน Wayground (เดิมคือ Quizizz) เป็นแบบฝึกหัดที่ครอบคลุมสำหรับนักเรียนที่กำลังเรียนรู้หลักการพื้นฐานในการพิสูจน์ความเท่ากันทุกประการของสามเหลี่ยม แบบฝึกหัดเหล่านี้ได้รับการออกแบบอย่างเชี่ยวชาญเพื่อเสริมสร้างทักษะการให้เหตุผลทางเรขาคณิตที่สำคัญ โดยแนะนำนักเรียนผ่านวิธีการที่เป็นระบบในการระบุด้านและมุมที่สอดคล้องกัน การประยุกต์ใช้หลักการด้าน-ด้าน-ด้าน, ด้าน-มุม-ด้าน และมุม-ด้าน-มุม และการสร้างบทพิสูจน์เชิงตรรกะ ชุดแบบฝึกหัดประกอบด้วยโจทย์ฝึกฝนที่หลากหลาย ตั้งแต่แบบฝึกหัดการระบุพื้นฐานไปจนถึงบทพิสูจน์หลายขั้นตอนที่ซับซ้อน โดยแต่ละแบบฝึกหัดมีเฉลยคำตอบโดยละเอียดที่สนับสนุนการเรียนรู้ด้วยตนเองและการประเมินตนเอง แบบฝึกหัดที่พิมพ์ได้ฟรีเหล่านี้เสนอการฝึกฝนอย่างเป็นระบบในการจดจำเครื่องหมายที่เท่ากันทุกประการ การเขียนประโยคแสดงความเท่ากันทุกประการโดยใช้สัญลักษณ์ที่ถูกต้อง และการพิจารณาว่าหลักการใดใช้ได้กับสามเหลี่ยมคู่ใด สร้างทักษะพื้นฐานที่จำเป็นสำหรับการเขียนบทพิสูจน์ทางเรขาคณิตขั้นสูง
Wayground (เดิมชื่อ Quizizz) ช่วยเสริมศักยภาพครูคณิตศาสตร์ด้วยคลังทรัพยากรมากมายนับล้านรายการที่สร้างโดยครูโดยเฉพาะ ซึ่งออกแบบมาสำหรับการสอนเรื่องสามเหลี่ยมที่เท่ากันทุกประการ มีฟังก์ชันการค้นหาและการกรองที่มีประสิทธิภาพ ช่วยให้ครูสามารถค้นหาสื่อที่สอดคล้องกับมาตรฐานเรขาคณิตของรัฐได้อย่างรวดเร็ว เครื่องมือการสร้างความแตกต่างของแพลตฟอร์มช่วยให้ครูสามารถปรับแต่งแบบฝึกหัดตามความต้องการของนักเรียนแต่ละคน โดยมีระดับความยากและประเภทของโจทย์ที่หลากหลายในหัวข้อเดียวกัน ครูสามารถเข้าถึงทรัพยากรเหล่านี้ได้อย่างราบรื่นทั้งในรูปแบบ PDF ที่พิมพ์ได้สำหรับการใช้งานในห้องเรียนแบบดั้งเดิม และรูปแบบดิจิทัลสำหรับสภาพแวดล้อมการเรียนรู้แบบโต้ตอบ ทำให้การวางแผนบทเรียนมีประสิทธิภาพและยืดหยุ่นมากขึ้น ชุดแบบฝึกหัดที่ครอบคลุมเหล่านี้สนับสนุนการแก้ไขปัญหาเฉพาะหน้าสำหรับนักเรียนที่ประสบปัญหา โอกาสในการเสริมสร้างความรู้สำหรับผู้เรียนที่มีความสามารถสูง และการฝึกฝนทักษะอย่างสม่ำเสมอซึ่งเสริมสร้างรูปแบบการคิดเชิงตรรกะที่จำเป็นสำหรับการเรียนรู้การพิสูจน์ทางเรขาคณิตอย่างเชี่ยวชาญ
