
25 คิว
9th
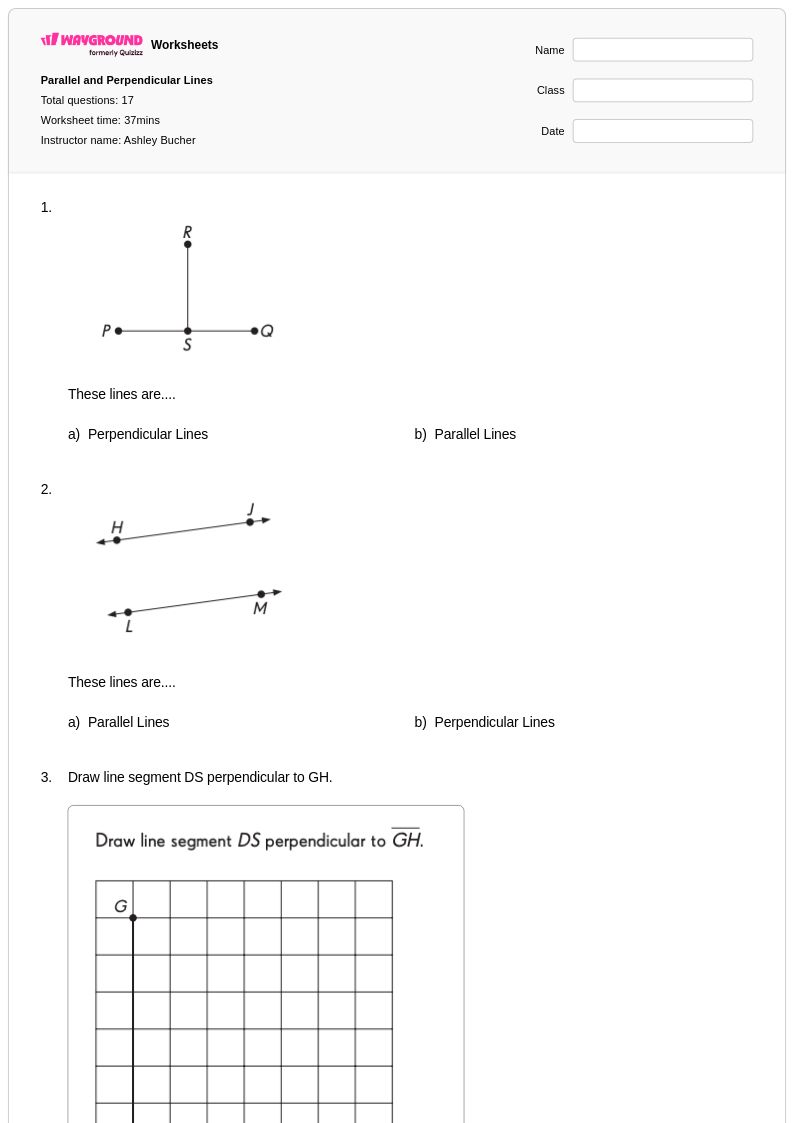
17 คิว
4th
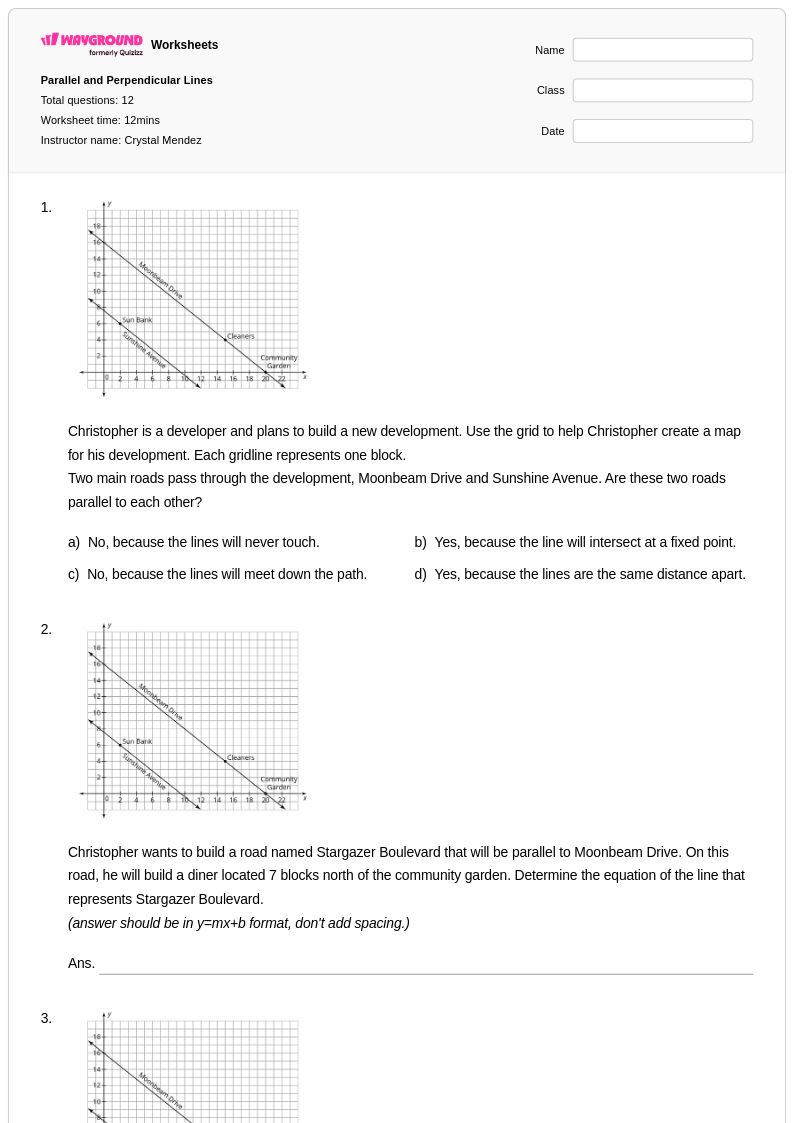
12 คิว
10th
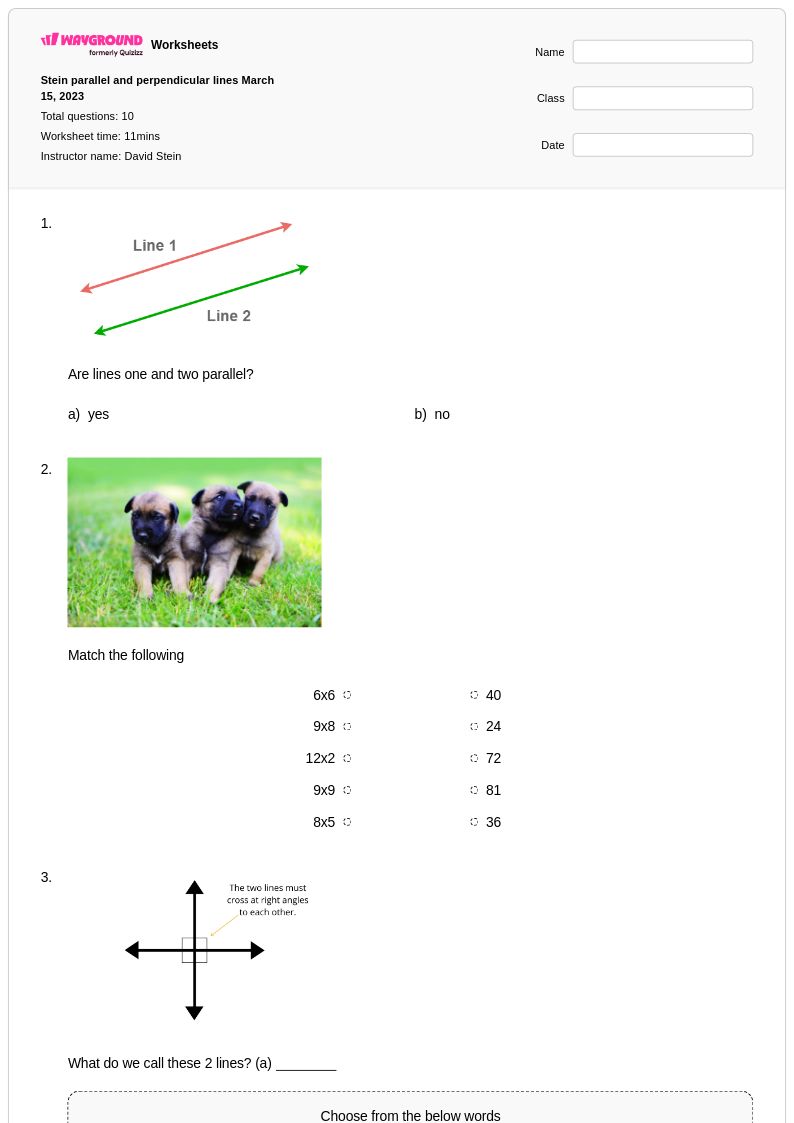
10 คิว
2nd

20 คิว
8th

11 คิว
9th - 12th

15 คิว
5th

25 คิว
9th
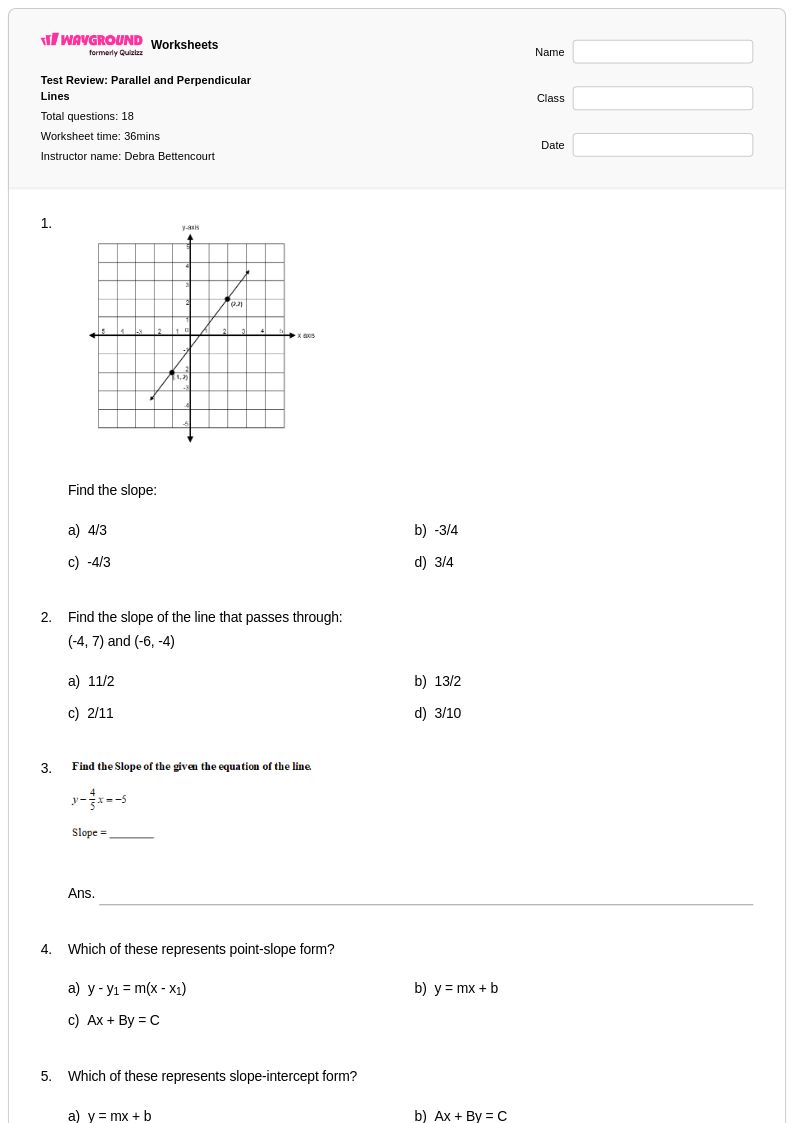
18 คิว
9th
20 คิว
10th - Uni
20 คิว
7th - 10th
20 คิว
9th - Uni
20 คิว
9th
20 คิว
9th - Uni

15 คิว
9th - Uni
10 คิว
9th - 12th

19 คิว
9th - Uni

20 คิว
10th - Uni

18 คิว
9th - 12th

20 คิว
11th - Uni
21 คิว
7th - 9th

15 คิว
8th

22 คิว
9th - 10th

22 คิว
9th
สำรวจแผ่นงานตามหัวเรื่อง
สำรวจแผ่นงาน เส้นขนานและเส้นตั้งฉาก ที่พิมพ์ได้
แบบฝึกหัดเส้นขนานและเส้นตั้งฉากจาก Wayground (เดิมคือ Quizizz) มอบโอกาสในการฝึกฝนอย่างครอบคลุมเพื่อให้นักเรียนเชี่ยวชาญความสัมพันธ์ทางเรขาคณิตพื้นฐานเหล่านี้ แหล่งข้อมูลทางการศึกษาเหล่านี้มุ่งเน้นการพัฒนาทักษะที่สำคัญ รวมถึงการระบุเส้นขนานและเส้นตั้งฉากในบริบทต่างๆ การทำความเข้าใจคุณสมบัติของความชันในเรขาคณิตพิกัด และการประยุกต์ใช้ความสัมพันธ์ของมุมที่เกิดขึ้นเมื่อเส้นขนานถูกตัดโดยเส้นตัดขวาง นักเรียนจะได้ทำแบบฝึกหัดที่มีโครงสร้างอย่างรอบคอบ ซึ่งค่อยๆ พัฒนาจากการระบุเส้นพื้นฐานไปสู่การประยุกต์ใช้ที่ซับซ้อนซึ่งเกี่ยวข้องกับนิพจน์พีชคณิตและการวิเคราะห์ระนาบพิกัด แบบฝึกหัดแต่ละชุดประกอบด้วยเฉลยคำตอบโดยละเอียดและมีให้ดาวน์โหลดฟรีในรูปแบบ PDF ที่สะดวก ช่วยให้ครูสามารถบูรณาการสื่อเหล่านี้เข้ากับการสอนคณิตศาสตร์ได้อย่างราบรื่น พร้อมทั้งให้ข้อเสนอแนะแก่นักเรียนเกี่ยวกับความเข้าใจของพวกเขาได้ทันที
Wayground (เดิมคือ Quizizz) ช่วยเสริมศักยภาพครูด้วยคลังข้อมูลขนาดใหญ่ที่มีทรัพยากรนับล้านรายการที่สร้างโดยครูโดยเฉพาะ ซึ่งออกแบบมาสำหรับการสอนเส้นขนานและเส้นตั้งฉากโดยเฉพาะ ความสามารถในการค้นหาและการกรองที่มีประสิทธิภาพของแพลตฟอร์มช่วยให้ครูสามารถค้นหาแบบฝึกหัดที่สอดคล้องกับมาตรฐานทางวิชาการเฉพาะและตรงกับระดับทักษะปัจจุบันของนักเรียนได้อย่างรวดเร็ว เครื่องมือการแบ่งระดับความยากง่ายขั้นสูงช่วยให้ครูสามารถปรับแต่งสื่อการเรียนการสอนที่มีอยู่ หรือสร้างชุดแบบฝึกหัดเฉพาะเจาะจงเพื่อการแก้ไขและเสริมสร้างความรู้ ทำให้มั่นใจได้ว่าผู้เรียนทุกคนจะได้รับความท้าทายที่เหมาะสม ชุดแบบฝึกหัดอเนกประสงค์เหล่านี้มีให้เลือกทั้งแบบพิมพ์ได้และแบบดิจิทัล รวมถึงไฟล์ PDF ที่ดาวน์โหลดได้ ทำให้เหมาะสำหรับการเรียนการสอนในห้องเรียน การบ้าน และการเรียนรู้ด้วยตนเอง ครูสามารถวางแผนลำดับบทเรียนที่ครอบคลุมได้อย่างมีประสิทธิภาพ ในขณะเดียวกันก็สามารถเข้าถึงประเภทของปัญหาที่หลากหลาย ซึ่งช่วยเสริมสร้างความเข้าใจในแนวคิดและสร้างความคล่องแคล่วในการระบุและทำงานกับความสัมพันธ์ของเส้นขนานและเส้นตั้งฉาก
